nLab homotopy
This page is about homotopy as a transformation. For homotopy sets in homotopy categories, see homotopy (as an operation).
Context
Homotopy theory
homotopy theory, (∞,1)-category theory, homotopy type theory
flavors: stable, equivariant, rational, p-adic, proper, geometric, cohesive, directed…
models: topological, simplicial, localic, …
see also algebraic topology
Introductions
Definitions
Paths and cylinders
Homotopy groups
Basic facts
Theorems
Type theory
natural deduction metalanguage, practical foundations
type theory (dependent, intensional, observational type theory, homotopy type theory)
computational trinitarianism =
propositions as types +programs as proofs +relation type theory/category theory
Contents
Idea
In many categories in which one does homotopy theory, there is a notion of homotopy between morphisms, which is closely related to the 2-morphisms in higher category theory: a homotopy between two morphisms is a way in which they are equivalent.
If we regard such a category as a presentation of an -category, then homotopies present the 2-cells in the resulting -category.
Definition
In topological spaces
Definition
For two continuous functions between topological spaces , then a left homotopy
is a continuous function
out of the standard cylinder object over : the product space of with the Euclidean closed interval , such that this fits into a commuting diagram of the form
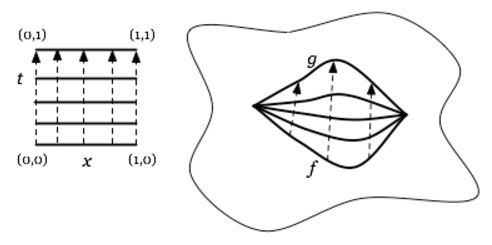
(graphics grabbed from J. Tauber here)
Example
Let be a topological space and let be two of its points, regarded as functions from the point to . Then a left homotopy, def. , between these two functions is a commuting diagram of the form
This is simply a continuous path in whose endpoints are and .
In enriched categories
If is enriched over Top, then a homotopy in between maps is a map in such that and . In itself this is the classical notion.
If has copowers, then an equivalent definition is a map , while if it has powers, an equivalent definition is a map .
There is a similar definition in a simplicially enriched category, replacing with the 1-simplex , with the caveat that in this case not all simplicial homotopies need be composable even if they match correctly. (This depends on whether or not all (2,1)-horns in the simplicial set, , have fillers.) Likewise in a dg-category we can use the “chain complex interval” to get a notion of chain homotopy.
In model categories
If is a model category, it has an intrinsic notion of homotopy determined by its factorizations. For more on the following see at homotopy in a model category.
Definition
Let be a model category and an object.
- A path object for is a factorization of the diagonal as
where is a weak equivalence. This is called a good path object if in addition is a fibration.
- A cylinder object for is a factorization of the codiagonal (or “fold map”) as
where is a weak equivalence. This is called a good cylinder object if in addition is a cofibration.
Remark
By the factorization axioms every object in a model category has both a good path object and as well as a good cylinder object according to def. . But in some situations one is genuinely interested in using non-good such objects.
For instance in the classical model structure on topological spaces, the obvious object is a cylinder object, but not a good cylinder unless itself is cofibrant (a cell complex in this case).
More generally, the path object of def. is analogous to the powering with an interval object and the cylinder object is analogous to the tensoring with an interval object. In fact, if is a -enriched model category and is fibrant/cofibrant, then these powers and copowers are in fact examples of (good) path and cylinder objects if the interval object is sufficiently good.
Definition
Let be two parallel morphisms in a model category.
- A left homotopy is a morphism from a cylinder object of , def. , such that it makes this diagram commute:
- A right homotopy is a morphism to some path object of , def. , such that this diagram commutes:
Remark
By remark it follows that in a -enriched model category, any enriched homotopy between maps is a left homotopy if is cofibrant and a right homotopy if is fibrant. Similar remarks hold for other enrichments.
For more see at homotopy in a model category.
In (co-)fibration categories
Clearly the concept of left homotopy in def. only needs part of the model category axioms and thus makes sense more generally in suitable cofibration categories. Dually, the concept of path objects in def. makes sense more generally in suitable fibration categories such as categories of fibrant objects in the sense of Brown.
Likewise if there is a cylinder functor, one gets functorially defined cylinder objects, etc.
In dependent type theory
In dependent type theory, let be a type and let be a type family indexed by , and let be two elements of a dependent product type of a type family . The type of homotopies between and is the type
A homotopy between and is simply an element .
Note that a homotopy is not the same as an identification . However this can be made so if one assumes function extensionality.
Related concepts
References
See also the references at homotopy theory and at model category.
Textbook accounts:
-
Anatoly Fomenko, Dmitry Fuchs, §3.1 in: Homotopical Topology, Graduate Texts in Mathematics 273, Springer (2016) [doi:10.1007/978-3-319-23488-5, pdf]
-
Adam Marsh: Fig. 4.2.2 in: Mathematics for Physics: An Illustrated Handbook, World Scientific (2018) [doi:10.1142/10816, book webpage]
Discussion in computational topology:
- Marek Filakovský, Lukáš Vokřínek, Are two given maps homotopic? An algorithmic viewpoint, Found Comput Math (2019) (arXiv:1312.2337, doi:10.1007/s10208-019-09419-x)
For homotopies in Martin-Löf dependent type theory:
- Univalent Foundations Project, Homotopy Type Theory – Univalent Foundations of Mathematics (2013)
Last revised on November 22, 2024 at 07:12:11. See the history of this page for a list of all contributions to it.