nLab
cosmic cube

Idea

The Cosmic Cube of higher category theory is the name for a diagram whose vertices correspond to special types of n-categories. The cube looks like this:

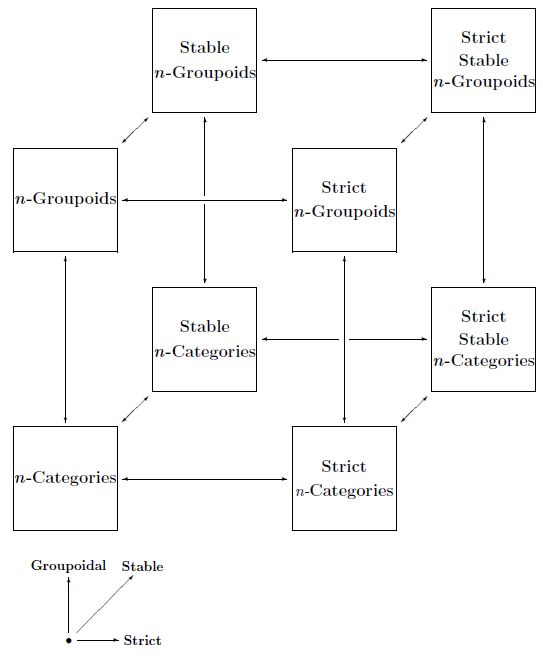
We may take $n=\mathrm{\infty }$ here as well, and we may also consider a version for (n,r)-categories. The three axes correspond to:

• making $n$-categories ‘groupoidal’ — that is, making morphisms invertible, thus passing from general $n$-categories to n-groupoids;

• making $n$-categories strict, thus passing from general $n$-categories to strict $n$-categories;

• making $n$-categories symmetric monoidal or ‘stable’, thus passing from general $n$-categories to symmetric monoidal $n$-categories.

In terms of homotopy theory

Each vertex of the cube can also be understood as corresponding to a version of homotopy theory:

$\mathrm{\infty }$-groupoids yield ordinary homotopy theory, symmetric monoidal and groupal $\mathrm{\infty }$-groupoids correspond to stable homotopy theory, strictly abelian strict $\mathrm{\infty }$-groupoids correspond to homological algebra. $\mathrm{\infty }$-Categories that are not $\mathrm{\infty }$-groupoids correspond to directed homotopy theory.

Vertices of the cube

Here we list the 8 vertices of the cube in the case of $\mathrm{\infty }$-categories.

Strict $\mathrm{\infty }$-categories

• strict ∞-category

Strict $\mathrm{\infty }$-groupoids

• strict ∞-groupoid

• crossed complex

Stably monoidal $\mathrm{\infty }$-categories

• k-tuply monoidal n-category

• stabilization hypothesis

• periodic table

Stably monoidal $\mathrm{\infty }$-groupoids

• ∞-group

• infinite loop space, spectrum

Strictly stably monoidal strict $\mathrm{\infty }$-groupoids

• chain complex, Dold-Kan correspondence

Etc.

(…)

Edges of the cube

Strict $\mathrm{\infty }$-groupoids in all $\mathrm{\infty }$-groupoids

A strict ∞-groupoid is modeled by a crossed complex. Under ω-nerve it embeds into all ∞-groupoids, modeled as Kan complexes.

$$\begin{array}{ccc}\mathrm{CrsCplx}& \stackrel{N^{\Delta }}{\hookrightarrow }& \mathrm{KanCplx}\\ \downarrow & & \downarrow \\ \mathrm{Str}\mathrm{\infty }\mathrm{Grpd}& \hookrightarrow & \mathrm{\infty }\mathrm{Grpd}\end{array}.$$\array{ CrsCplx &\stackrel{N^\Delta}{\hookrightarrow}& KanCplx \\ \downarrow && \downarrow \\ Str \infty Grpd &\hookrightarrow& \infty Grpd } \,.

Strictly stable strict $\mathrm{\infty }$-groupoids in strict $\mathrm{\infty }$-groupoids

A strictly stable strict ∞-groupoid is modeled by a bounded-below chain complex of abelian groups. Under the embedding $\Theta$ of complexes into crossed complexes it embeds into strict ∞-groupoids.

$$\begin{array}{ccc}\mathrm{ChnCplx}& \stackrel{\Theta }{\hookrightarrow }& \mathrm{CrsCplx}\\ \downarrow & & \downarrow \\ \mathrm{StrAb}\mathrm{Str}\mathrm{\infty }\mathrm{Grpd}& \hookrightarrow & \mathrm{Str}\mathrm{\infty }\mathrm{Grpd}\end{array}.$$\array{ ChnCplx &\stackrel{\Theta}{\hookrightarrow}& CrsCplx \\ \downarrow && \downarrow \\ StrAb Str \infty Grpd &\hookrightarrow& Str \infty Grpd } \,.

For the definition of $\Theta$ see Nonabelian Algebraic Topology , section Crossed complexes from chain complexes.

Strictly stable strict $\mathrm{\infty }$-groupoids in all $\mathrm{\infty }$-groupoids

Combining the above inclusions

$$\begin{array}{ccccc}\mathrm{ChainCplx}& \stackrel{\Theta }{\hookrightarrow }& \mathrm{CrossedCplx}& \stackrel{N^{\Delta }}{\hookrightarrow }& \mathrm{KanCplx}\\ {\downarrow }^{\simeq }& & {\downarrow }^{\simeq }& & {\downarrow }^{\simeq }\\ \mathrm{StrAb}\mathrm{Str}\mathrm{\infty }\mathrm{Grpd}& \hookrightarrow & \mathrm{Str}\mathrm{\infty }\mathrm{Grpd}& \hookrightarrow & \mathrm{\infty }\mathrm{Grpd}\end{array}$$\array{ ChainCplx &\stackrel{\Theta}{\hookrightarrow}& CrossedCplx &\stackrel{N^\Delta}{\hookrightarrow}& KanCplx \\ \downarrow^{\mathrlap{\simeq}} && \downarrow^{\mathrlap{\simeq}} && \downarrow^{\mathrlap{\simeq}} \\ StrAb Str\infty Grpd &\hookrightarrow& Str \infty Grpd &\hookrightarrow& \infty Grpd }

yields in total the map $\mathrm{ChnCplx}\to \mathrm{sAb}$ from chain complexes to simplicial abelian groups (followed by the forgetful $\mathrm{sAb}\to \mathrm{KanCpx}$) of the Dold-Kan correspondence.

Strictly stable strict $\mathrm{\infty }$-groupoids in strictly stable $\mathrm{\infty }$-groupoids

A strictly stable strict ∞-groupoid is modeled by a bounded-below chain complex of abelian groups. Under ω-nerve it embeds into all (connective) spectras, modeled as spectrum objects in Kan complexes.

$$\begin{array}{ccc}{\mathrm{ChnCplx}}^{+}& \stackrel{{\Sigma }^{\mathrm{\infty }}{N}^{\Delta }\Theta }{\hookrightarrow }& \mathrm{Sp}(\mathrm{KanCplx})\\ \downarrow & & \downarrow \\ \mathrm{StrAb}\mathrm{Str}\mathrm{\infty }\mathrm{Grpd}& \hookrightarrow & \mathrm{Sp}(\mathrm{\infty }\mathrm{Grpd})\end{array}.$$\array{ ChnCplx^+ &\stackrel{\Sigma^\infty \N^\Delta \Theta}{\hookrightarrow}& Sp(KanCplx) \\ \downarrow && \downarrow \\ StrAb Str \infty Grpd &\hookrightarrow& Sp(\infty Grpd) } \,.

Strictly stable $\mathrm{\infty }$-groupoids in all $\mathrm{\infty }$-groupoids

A strictly stable ∞-groupoid is modeled by a connective spectrum. The forgetful functor to ∞-groupoids is also called ${\Omega }^{\mathrm{\infty }}$ or the “zeroth-space functor.”

References

• John Baez, What $n$-Categories Should Be Like.

• Some blog discussion