nLab judgment
Context
Type theory
natural deduction metalanguage, practical foundations
type theory (dependent, intensional, observational type theory, homotopy type theory)
computational trinitarianism =
propositions as types +programs as proofs +relation type theory/category theory
Foundations
The basis of it all
Set theory
- fundamentals of set theory
- material set theory
- presentations of set theory
- structuralism in set theory
- class-set theory
- constructive set theory
- algebraic set theory
Foundational axioms
-
basic constructions:
-
strong axioms
-
further
Removing axioms
Judgments
Idea
In mathematics and especially in formal logic, by a judgement [Frege (1879, §2)] one means the assertion [Russell & Whitehead (1910, p. xviii)] or validation [Kochen (1961, p. 2)] of a proposition , hence the claim (or even the specification) of a proof of [Church (1940, §5)].
To bring out the subtle (cf. jstor:43154266) but crucial distinction — eloquently amplified by Martin-Löf (1996, lectures 1-2) — between the notion of a proposition as such and the judgement/assertion/validation/proof of its truth, it is tradition to prefix the latter with the symbol “”, known as the Urteilsstrich (German: “judgement stroke”) of [Frege (1879, §2)] (see the historical pointers below), as:
For example, the Riemann hypothesis certainly is a proposition, but it remains open whether we may truthfully assert or validate it, hence we cannot yet judge that it holds true: No proof is known, even though it seems likely to be in fact true.
In other words, the judgement symbols “ ” convey that we know (a proof of, hence the truth of) [Martin-Löf (1996, lectures 1-2)].
As such, judgements may be formalized as “meta-proposition”, namely propositions but in an ambient meta-language (the deductive system or logical framework) rather than in the object language in which the given itself is formulated. (More specifically, any deductive system includes, as part of its specification, which strings of symbols are to be regarded as the judgments. Some of these symbols may themselves express a proposition in the object language, but this is not necessarily the case.)
More generally, one considers hypothetical judgements (maybe first made explicit in [Church (1940, §5)]) which are such assertions/validations but conditioned on premises, hence claims/specifications of proofs based on assumptions : Writing
is to express the judgement that given any assertion/validation/proof of we know how to produce (from that) a validation/proof of .
In systems of (dependent) type theory (where such notation seems to go back to Hofmann (1995, p. 31), cf. below) this is quite literally the case in that the categorical semantics of such a hypothetical judgement is a given by a function (and typically a computable function, hence an algorithm) which maps proofs of to proofs of .
More generally yet, in type theory the propositions and appearing here are allowed to be any (dependent) types (see at propositions as types). In this generality, the denotational semantics of hypothetical judgements (2) is given by (computable) functions/morphisms with domain and codomain . In programming languages based on such type theories this translates to the denotation of an actual program which produces data of data type when run on input data of data type .
Judgements are themselves subject to a calculus of natural deduction by which further judgements may be inferred from given ones. For example the notation
traditionally expresses that whenever we can assert both as well as assuming a validation of (hence: given a pair of functions with domain type ), then with that same assumption we find assertion/validation/proof of their logical conjunction (namely a function with codomain to their product type).
Finally, to make explicit which particular assumptions a hypothetical judgement really depends on, it is common to adjoin a generic context symbol to the hypothesis on the left hand side of the Urteilsstrich: Notation such as
expresses the judgement that may be asserted given validation of , but that in doing so only the validation of is actually made use of, while may be any context of assumptions (whose validation might however be used in previous/further deduction steps).
Examples
In first-order logic
In first-order logic, a paradigmatic example of a judgement is the judgement that a certain string of symbols is a well-formed proposition. This is often written as “”, where is a metavariable standing for a string of symbols that denotes a proposition.
Another example of a judgement is the judgement that these symbols form a proposition proved to be true. This judgment is often written as “”.
Neither of these judgements is the same thing as the proposition itself. In particular, the proposition is a statement in the logic, while the judgement that the proposition is a proposition, or is provably true, is a statement about the logic. However, often people abuse notation and conflate a proposition with the judgment that it is true, writing instead of .
In type theory
The distinction between judgements and propositions is particularly important in intensional type theory.
The paradigmatic example of a judgment in type theory is a typing judgment. The assertion that a term has type (written “”) is not a statement in the type theory (that is, not something which one could apply logical operators to in the type-theoretic system) but a statement about the type theory.
Often, type theories include only a particular small set of judgments, such as:
-
typing judgments (written , as above)
-
judgments of typehood (usually written )
-
judgments of equality between typed terms (written say )
(In a type theory with a type of types, judgments of typehood can sometimes be incorporated as a special case of typing judgments, writing instead of .)
These limited sets of judgments are often defined inductively by giving type formation/term introduction/term elimination- and computation rules (see natural deduction) that specify under what hypotheses one is allowed to conclude the given judgment.
These inductive definitions can be formalized by choosing a particular type theory to be the meta-language; usually a very simple type theory suffices (such as a dependent type theory with only dependent product types). Such a meta-type-theory is often called a logical framework.
Hypothetical and generic judgments
It may happen that a judgment is only derivable under the assumptions of certain other judgments . In this case one writes
Often, however, it is convenient to incorporate hypotheticality into judgments themselves, so that becomes a single hypothetical judgment. It can then be a consequence of other judgments, or (more importantly) a hypothesis used in concluding other judgments. For instance, in order to conclude the truth of an implication , we must conclude assuming ; thus the introduction rule for implication is
with a hypothetical judgment as its hypothesis. See natural deduction for a more extensive discussion.
In a type theory, we may also consider the case where the hypotheses are typing judgments of the form , where is a variable, and in which the conclusion judgment involves these variables as free variables. For instance, could be , where is a valid (well-formed) proposition only when has a specific type . In this case we have a generic judgement, written
which expresses that assuming the hypothesis or antecedent judgement that is of type , as a consequence we have the succedent judgement that is a proposition. If on the right here we have a typing judgment
we have a term in context.
For more about the precise relationship between the various meanings of here, see natural deduction and logical framework.
While this may seem to be a very basic form of (hypothetical/generic) judgement only, in systems such as dependent type theory or homotopy type theory, all of logic and a good bit more is all based on just this.
History of the notion and notation

The terminology of judgement in formal logic, and the notation
for the judgement of content is due to Frege (1879, §2) (Frege’s das Urtheil – or das Urteil in modern German spelling – directly translates to: the judgement).
This notion and notation (often “Frege’s Urteilsstrich” – “judgement stroke”) was adopted by Russell & Whitehead (1910, p. xviii), who however speak of “assertion” instead of “judgement” — see Martin-Löf (1996, p. 6) for speculation that these authors may have wanted “to avoid any association with Kantian philosophy” (cf. below):
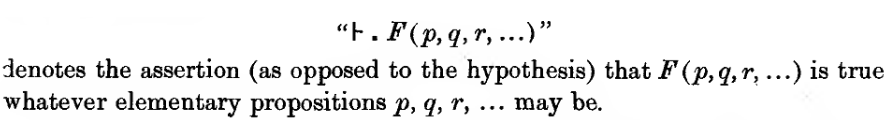
and then by Church (1940, §5) (without any attribution) — now allowing hypotheses/assumptions on the left of the Urteilsstrich — to mean provable under these assumptions:
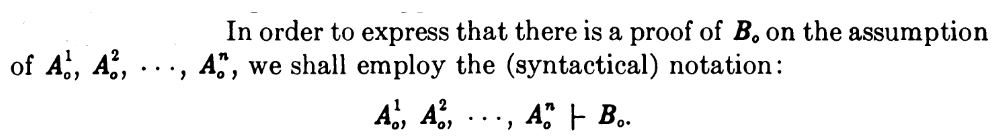
Similarly, Kochen (1961, p. 2) introduced (in a context of model theory) the notation “” (apparently not actively remembering its historical origin, cf. Kochen (2017)) for a notion in model theory pronounced “ validates ” — which is at least closely related to these hypothetical judgements (and often used synonymously, e.g. here):
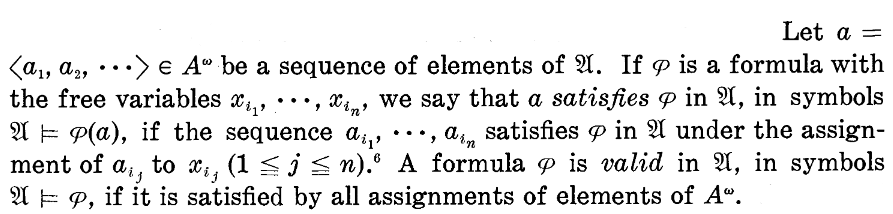
The need (which had been contested by some logicians such as Wittgenstein, cf. jstor:43154266) for Frege’s distinction between a proposition “”, as such, and its judgement/assertion/proof/validation “” was eloquently argued for by Martin-Löf (1984, pp. 2), (1987) and in (1996, lectures 1-2), together with a re-promotion of Frege’s Urteilsstrich notation “” (ML84, p. 2, ML96, p. 2, 6):

The notation for hypothetical judgements
was then (without attribution to Church or Martin-Löf) adopted for dependent type theory in Hofmann (1995, p. 31), later published as Hofmann (1997, p. 82):

This eventually became the trademark of the practice of dependent type theory (though mostly used without any attribution), e.g.: Jacobs (1998, p. 2, 121, 586); Bauer, Haselwarter & Lumsdaine (2020).
(Curiously, apparently Martin-Löf did not actually use the general notation (3) in publications: When in 1996, p. 29 it comes to hypothetical judgements, he switched to using just a vertical “” instead of “”.)
In summary:
| terminology | author |
|---|---|
| judgement | Frege (1879) |
| assertion | Russell & Whitehead (1910) |
| proof | Church (1940) |
| validation | Kochen (1961) |
| judgement | Martin-Löf (1984, 1996) Hofmann (1995, 1997) |
Related concepts
mathematical statements
References
Pre-history of the notion of judgement (Urteil) in (informal) logic:
-
Georg Hegel, first section, second chapter of Science of Logic (1813)
-
Franz Brentano, Psychologie vom empirischen Standpunkte (1874) [web]
see: SEP: Brentano’s Theory of Judgement
The origin of the notion of “judgement” (and of the notation “” for it) in formal logic:
- Gottlob Frege, Begriffsschrift (1879) [web scan, Wikipedia entry]
and under the name “assertion” in:
- Bertrand Russell, Alfred Whitehead, p. xviii in: Principia Mathematica (1910)
Keeping the symbol “”, now allowing hypothesis on the left, but pronouning it as “proof under assumptions”:
-
Alonzo Church, §5 of: A Formulation of the Simple Theory of Types, The Journal of Symbolic Logic 5 2 (1940) 56-68 [doi:10.2307/2266170]
(see also at simple type theory)
Discussion in the context of what became known as Martin-Löf dependent type theory:
-
Per Martin-Löf (notes by Giovanni Sambin), p. 2-4 in: Intuitionistic type theory, Lecture in Padua 1984, Bibliopolis (1984) [pdf, pdf]
-
Per Martin-Löf, Truth of a proposition, evidence of a judgement, validity of a proof, Synthese 73 (1987) 407–420 [doi:10.1007/BF00484985, pdf]
-
Per Martin-Löf, A path from logic to metaphysics, talk at Nuovi problemi della logica e della filosofia della scienza, Jan 1990 (pdf)
-
Per Martin-Löf, On the Meanings of the Logical Constants and the Justifications of the Logical Laws, Nordic Journal of Philosophical Logic, 1 1 (1996) 11-60 [pdf, pdf]
-
Martin Hofmann, §2.1.2 in: Syntax and semantics of dependent types, Chapter 2 in: Extensional concepts in intensional type theory, Ph.D. thesis, University of Edinburgh (1995), Distinguished Dissertations, Springer (1997) [ECS-LFCS-95-327, pdf, doi:10.1007/978-1-4471-0963-1]
also published as:
-
Martin Hofmann, p. 82 of: Syntax and semantics of dependent types, in Semantics and logics of computation, Publ. Newton Inst. 14, Cambridge Univ. Press (1997) 79-130 [doi:10.1017/CBO9780511526619.004]
Reviewed in:
- Frank Pfenning, Rowan Davies, §2, §3 of: A judgemental reconstruction of modal logic, Mathematical Structures in Computer Science 11 4 (2001) 511-540 [doi:10.1017/S0960129501003322, pdf]
Further discussion in
- Greta Coraglia, Ivan Di Liberti, Context, Judgement, Deduction [arXiv:2111.09438]
Textbook acccount in a context of programming languages:
- Robert Harper, section I.3 of Practical Foundations for Programming Languages (2015)
The alternative notation “” for satisfaction with closely related (if different) usage seems to originate in
- Simon Kochen, p. 223 in: Ultraproducts in the Theory of Models, Ann. Math. 74 2 (1961) 221-261 [doi:10.2307/1970235]
whose author
cannot recollect whether [he] originated it or took it from some other paper.
according to:
- Simon Kochen, Origins of the double turnstile, FOM mailing list posting (Feb 2017) [web, screenshot]
See also:
- Formal Logic Wikibook: Satisfaction
Last revised on February 6, 2024 at 03:12:37. See the history of this page for a list of all contributions to it.