nLab Dp-D(p+2)-brane intersections in fuzzy funnels -- section

Transveral Dp-D(p+2)-brane intersections in fuzzy funnels

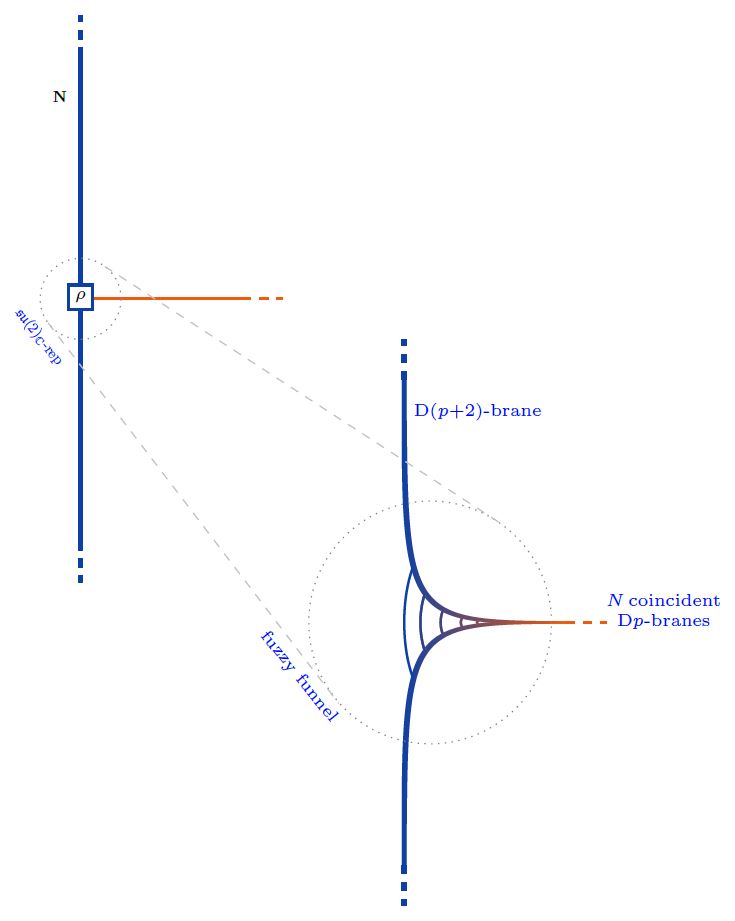
The boundary condition in the nonabelian DBI model of coincident Dp-branes describing their transversal intersection/ending with/on D(p+2)-branes is controled by Nahm's equation and thus exhibits the brane intersection-locus equivalently as:

1. a fuzzy funnel noncommutative geometry interpolating between the $\mathrm{D}p$- and the $\mathrm{D}(p+2)$-brane worldvolumes;

2. geometric engineering of Yang-Mills monopoles in the worldvolume-theory of the ambient $D(p+2)$-branes.

(Diaconescu 97, Constable-Myers-Fafjord 99, Hanany-Zaffaroni 99, Gaiotto-Witten 08, Section 2.4, HLPY 08, GZZ 09)

More explicitly, for $y \in (0,\infty ]$ the transversal distance along the stack of $N$ $\mathrm{D}p$-branes away from the $\mathrm{D}(p+2)$-brane, and for

$$X^i \in C^\infty\big( (0,\infty], \mathfrak{u}(N) \big) \phantom{AAA} i \in \{1,2,3\}$$

the three scalar fields on the worldvolume, the boundary condition is:

$$\frac{d}{d y} X^3 + [X^1, X^2] \;=\; 0 \,, \;\;\; \frac{d}{d y} X^1 + [X^2, X^3] \;=\; 0 \,, \;\;\; \frac{d}{d y} X^2 + [X^3, X^1] \;=\; 0$$

as $y \to 0$. These are Nahm's equations, solved by

$$X^i(y) = \frac{1}{y} \rho^i + \text{non-singular}$$

where

$$\rho \;\colon\; \mathfrak{su}(2) \longrightarrow \mathfrak{u}(N)$$

is a Lie algebra homomorphism from su(2) to the unitary Lie algebra, and

$$\rho^i \coloneqq \rho(\sigma^i)$$

is its complex-linear combination of values on the canonical Pauli matrix basis.

Equivalently. $\rho$ is an $N$-dimensional complex Lie algebra representation of su(2). Any such is reducible as a direct sum of irreducible representations $\mathbf{N}^{(M5)}$, for which there is exactly one, up to isomorphism, in each dimension $N^{(M5)} \in \mathbb{N}$:

(1)$$\rho \;\simeq\; \underset{ i }{\bigoplus} \big( N_i^{(M2)} \cdot \mathbf{N}_i^{(M5)} \big) \,.$$

(Here the notation follows the discussion at M2/M5-brane bound states in the BMN model, which is the M-theory lift of the present situation).

Now each irrep $\mathbf{N}_i^{(M5)}$ may be interpreted as a fuzzy 2-sphere of radius $\propto \sqrt{ \left( N_i^{(M5)}\right)^2 - 1 }$, hence as the section of a fuzzy funnel at given $y = \epsilon$, whence the totality of (1) represents a system of concentric fuzzy 2-spheres/fuzzy funnels.

graphics from Sati-Schreiber 19c

Moreover, since the complexification of su(2) is the complex special linear Lie algebra $\mathfrak{sl}(2,\mathbb{C})$ (here) the solutions to the boundary conditions are also identified with finite-dimensional $\mathfrak{sl}(2,\mathbb{C})$ Lie algebra representations:

(2)$$\rho \;\in\; \mathfrak{sl}(2,\mathbb{C}) Rep \,.$$

This is what many authors state, but it is not yet the full picture:

Also the worldvolume Chan-Paton gauge field component $A$ along $y$ participates in the brane intersection

$$A \in C^\infty\big( (0,\infty], \mathfrak{u}(N) \big)$$

its boundary condition being that

$$[A, X^i] \;=\; 0 \phantom{AAAA} \text{for all}\; i \in \{1,2,3\}$$

as $y \to 0$ (Constable-Myers 99, Section 3.3, Thomas-Ward 06, p. 16, Gaiotto-Witten 08, Section 3.1.1)

Together with (2) this means that the quadruple of fields $(X^1,X^2,X^3,A)$ constitutes a Lie algebra representation of the general linear Lie algebra

$$\mathfrak{gl}(2,\mathbb{C}) \;\simeq\; \underset{ \langle X^1, X^2, X^3 \rangle }{ \underbrace{ \mathfrak{sl}(2,\mathbb{C}) } } \oplus \underset{ \langle A \rangle }{ \underbrace{ \mathbb{C} } }$$

This makes little difference as far as bare Lie algebra representations are concerned, but it does make a crucial difference when these are regarded as metric Lie representations of metric Lie algebras, since $\mathfrak{gl}(2,\mathbb{C})$ admits further invariant metrics…