nLab Nahm's equation
Context
Chern-Weil theory
Ingredients
Connection
Curvature
Theorems
Algebraic Quantum Field Theory
algebraic quantum field theory (perturbative, on curved spacetimes, homotopical)
Concepts
quantum mechanical system, quantum probability
interacting field quantization
Theorems
States and observables
Operator algebra
Local QFT
Perturbative QFT
Contents
Idea
(…)
Properties
Transveral Dp-D(p+2)-brane intersections in fuzzy funnels
The boundary condition in the nonabelian DBI model of coincident Dp-branes describing their transversal intersection/ending with/on D(p+2)-branes is controled by Nahm's equation and thus exhibits the brane intersection-locus equivalently as:
-
a fuzzy funnel noncommutative geometry interpolating between the - and the -brane worldvolumes;
-
geometric engineering of Yang-Mills monopoles in the worldvolume-theory of the ambient -branes.
(Diaconescu 97, Constable-Myers-Fafjord 99, Hanany-Zaffaroni 99, Gaiotto-Witten 08, Section 2.4, HLPY 08, GZZ 09)
More explicitly, for the transversal distance along the stack of -branes away from the -brane, and for
the three scalar fields on the worldvolume, the boundary condition is:
as . These are Nahm's equations, solved by
where
is a Lie algebra homomorphism from su(2) to the unitary Lie algebra, and
is its complex-linear combination of values on the canonical Pauli matrix basis.
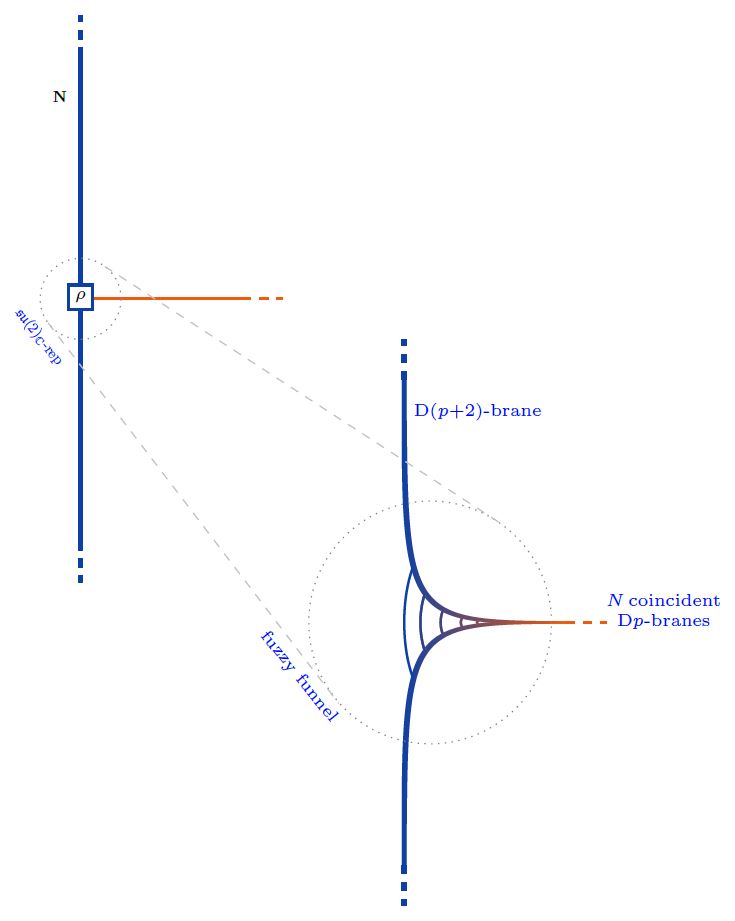
Equivalently. is an -dimensional complex Lie algebra representation of su(2). Any such is reducible as a direct sum of irreducible representations , for which there is exactly one, up to isomorphism, in each dimension :
(Here the notation follows the discussion at M2/M5-brane bound states in the BMN model, which is the M-theory lift of the present situation).
Now each irrep may be interpreted as a fuzzy 2-sphere of radius , hence as the section of a fuzzy funnel at given , whence the totality of (1) represents a system of concentric fuzzy 2-spheres/fuzzy funnels.
graphics from Sati-Schreiber 19c
Moreover, since the complexification of su(2) is the complex special linear Lie algebra (here) the solutions to the boundary conditions are also identified with finite-dimensional Lie algebra representations:
This is what many authors state, but it is not yet the full picture:
Also the worldvolume Chan-Paton gauge field component along participates in the brane intersection
its boundary condition being that
as (Constable-Myers 99, Section 3.3, Thomas-Ward 06, p. 16, Gaiotto-Witten 08, Section 3.1.1)
Together with (2) this means that the quadruple of fields constitutes a Lie algebra representation of the general linear Lie algebra
This makes little difference as far as bare Lie algebra representations are concerned, but it does make a crucial difference when these are regarded as metric Lie representations of metric Lie algebras, since admits further invariant metrics…
Related concepts
References
General
The original articles;
-
Werner Nahm, The construction of all self-dual multi-monopoles by the ADHM method, In: Craigie et al. (eds.), Monopoles in quantum theory, Singapore, World Scientific 1982 (spire:178340)
-
Werner Nahm, Self-dual monopoles and calorons, In: G. Denardo, G. Ghirardi and T. Weber (eds.), Group theoretical methods in physics, Lecture Notes in Physics 201. Berlin, Springer-Verlag 1984 (doi:10.1007/BFb0016145)
-
Simon Donaldson, Nahm’s Equations and the Classification of Monopoles, Comm. Math. Phys., Volume 96, Number 3 (1984), 387-407, (euclid:cmp.1103941858)
Further discussion:
- Rafe Mazzeo, Edward Witten, The Nahm Pole Boundary Condition, In: The influence of Solomon Lefschetz in geometry and topology, Contemporary Mathematics 621 (2014): 171 (arXiv:1311.3167, doi:10.1090/conm/621)
Review:
-
Marcos Jardim, A survey on Nahm transform, J Geom Phys 52 (2004) 313-327 (arxiv:math/0309305)
-
Reinier Storm, The Yang-Mills Moduli Space and The Nahm Transform (dspace:1874/285043)
See also
- Wikipedia, Nahm equations
In terms of Coulomb branch singularities in SYM
In terms of Coulomb branch singularities on super Yang-Mills theories:
- Mathew Bullimore, Tudor Dimofte, Davide Gaiotto, The Coulomb Branch of 3d Theories, Commun. Math. Phys. (2017) 354: 671 (arXiv:1503.04817)
In term of Dp-D(p+2) brane intersections
On transversal Dp-D(p+2) brane intersections as Yang-Mills monopoles / fuzzy funnel-solutions to Nahm's equation:
For transversal D1-D3 brane intersections:
-
Duiliu-Emanuel Diaconescu, D-branes, Monopoles and Nahm Equations, Nucl. Phys. B503 (1997) 220-238 (arxiv:hep-th/9608163)
-
Amihay Hanany, Edward Witten, Type IIB Superstrings, BPS Monopoles, And Three-Dimensional Gauge Dynamics, Nucl. Phys. B492:152-190, 1997 (arxiv:hep-th/9611230)
-
Jessica K. Barrett, Peter Bowcock, Using D-Strings to Describe Monopole Scattering (arxiv:hep-th/0402163)
-
Jessica K. Barrett, Peter Bowcock, Using D-Strings to Describe Monopole Scattering - Numerical Calculations (arxiv:hep-th/0512211)
For transversal D2-D4-brane bound states (with an eye towards AdS/QCD):
- Alexander Gorsky, Valentin Zakharov, Ariel Zhitnitsky, On Classification of QCD defects via holography, Phys. Rev. D79:106003, 2009 (arxiv:0902.1842)
For transversal D3-D5 brane intersections:
- Davide Gaiotto, Edward Witten, Supersymmetric Boundary Conditions in N=4 Super Yang-Mills Theory, J Stat Phys (2009) 135: 789 (arXiv:0804.2902)
For transversal D6-D8 brane intersections (with an eye towards AdS/QCD):
- Deog Ki Hong, Ki-Myeong Lee, Cheonsoo Park, Ho-Ung Yee, Section V of: Holographic Monopole Catalysis of Baryon Decay, JHEP 0808:018, 2008 (https:arXiv:0804.1326)
and as transversal D6-D8-brane bound states on a half NS5-brane in type I' string theory:
- Amihay Hanany, Alberto Zaffaroni, Monopoles in String Theory, JHEP 9912 (1999) 014 (arxiv:hep-th/9911113)
Making explicit the completion of the -representation to a -representation by adjoining the gauge field component to the scalar fields :
-
Sergey Cherkis, Instantons on Gravitons, around (21) in: Commun. Math. Phys. 306:449-483, 2011 (arXiv:1007.0044)
Lift to M-theory
The lift of Dp-D(p+2)-brane bound states in string theory to M2-M5-brane bound states/E-strings in M-theory, under duality between M-theory and type IIA string theory+T-duality, via generalization of Nahm's equation (this eventually motivated the BLG-model/ABJM model):
-
Anirban Basu, Jeffrey Harvey, The M2-M5 Brane System and a Generalized Nahm’s Equation, Nucl.Phys. B713 (2005) 136-150 (arXiv:hep-th/0412310)
-
Jonathan Bagger, Neil Lambert, Sunil Mukhi, Constantinos Papageorgakis, Section 2.2.1 of Multiple Membranes in M-theory, Physics Reports, Volume 527, Issue 1, 1 June 2013, Pages 1-100 (arXiv:1203.3546, doi:10.1016/j.physrep.2013.01.006)
Last revised on February 1, 2020 at 15:57:22. See the history of this page for a list of all contributions to it.