nLab Lie algebra representation
Context
Representation theory
geometric representation theory
Ingredients
Definitions
representation, 2-representation, ∞-representation
Geometric representation theory
-
Grothendieck group, lambda-ring, symmetric function, formal group
-
principal bundle, torsor, vector bundle, Atiyah Lie algebroid
-
Eilenberg-Moore category, algebra over an operad, actegory, crossed module
Theorems
Lie theory
∞-Lie theory (higher geometry)
Background
Smooth structure
Higher groupoids
Lie theory
∞-Lie groupoids
∞-Lie algebroids
Formal Lie groupoids
Cohomology
Homotopy
Related topics
Examples
-Lie groupoids
-Lie groups
-Lie algebroids
-Lie algebras
Contents
Idea
The representation/action of a Lie algebra on a vector space .
Definition
A Lie algebra representation is a Lie algebra homomorphism to the endomorphism Lie algebra of .
This means equivalently that
is a bilinear map such that for all and we have the Lie action property:
Properties
In terms of string diagrams / Jacobi diagrams
In string diagram-notation for Lie algebra objects internal to tensor categories, the Lie action property (1) looks as follows:
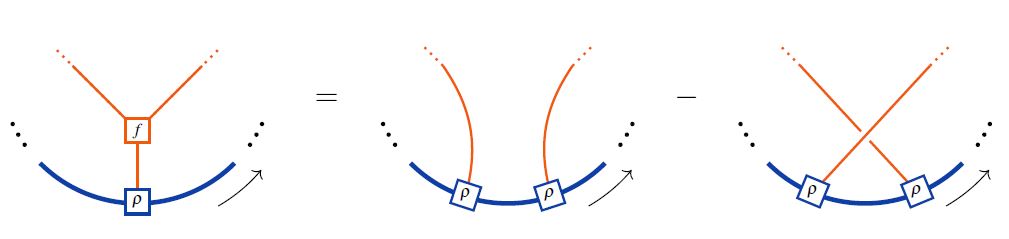
Here the last line shows the equivalence to the Jacobi identity on the Lie algebra object itself in the case that the Lie action is the adjoint action.
In the language of Jacobi diagrams this is called the STU-relation, and is the reason behind the existence of Lie algebra weight systems in knot theory.
Related concepts
References
See also
- Wikipedia, Lie algebra representation
Last revised on May 1, 2021 at 08:19:41. See the history of this page for a list of all contributions to it.