nLab comparison functor
Context
Category theory
Concepts
Universal constructions
Theorems
Extensions
Applications
Categorical algebra
internalization and categorical algebra
-
algebra object (associative, Lie, …)
Contents
Idea
While every functor might be understood as constituting a “comparison” between its domain and codomain-categories, the term “comparison functor” is often understood by default as referring, in categorical algebra, to the unique functor that relates any adjunction to its monadic adjunction – this is the case we discuss here.
But other instances of functorial “comparison” are bound to be relevant. For instance, for the “comparison lemma” in topos theory see there.
Statement
Proposition
(the comparison functor from any adjunction to its monadic adjunction)
Every pair of adjoint functors (with unit and counit ) between categories , fits into a commuting diagram in Cat of the following form:
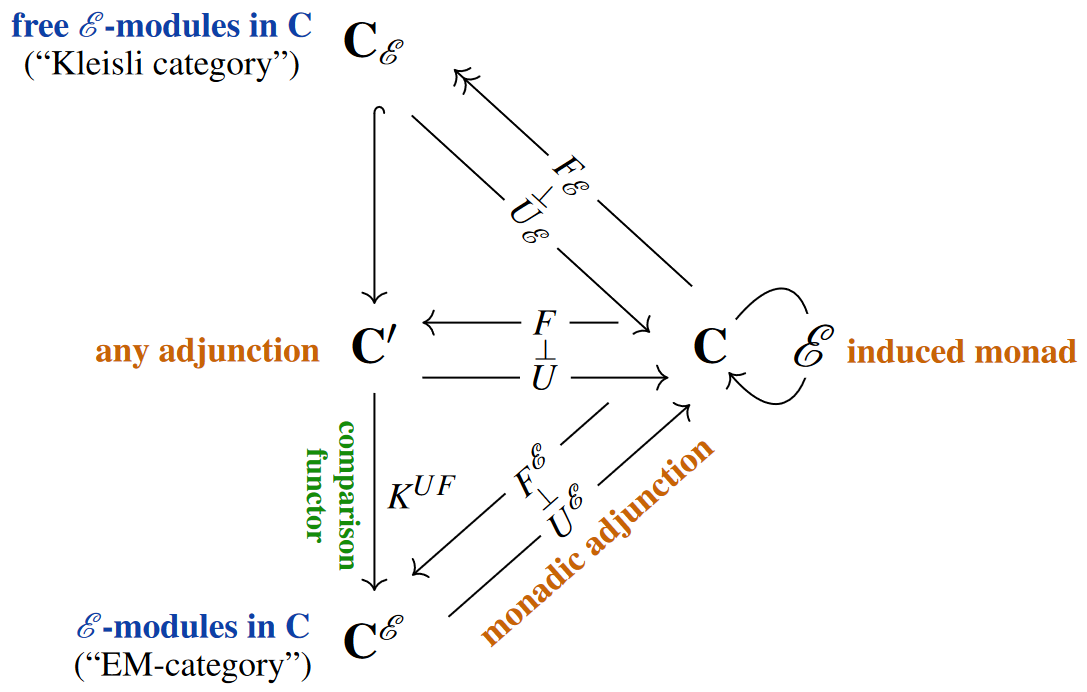
Here:
-
denotes the induced endofunctor on
which carries the structure of a monad with
-
unit given by
-
product given by
-
-
denotes the (“Eilenberg-Moore”-)category of -algebras in
in with homomorphisms between them,
-
denotes the “comparison functor” given by
-
Here the last line makes explicit that
In fact, and this realizes the monadic adjunction whose induced monad is .
Hence the original is monadic iff the comparison functor is an equivalence of categories.
(See for instance MacLane (1971), §VI.3)
Properties
-
is fully faithful if and only if is of descent type. In this case, has a right adjoint if and only if it is essentially surjective if and only if it is an equivalence of categories, since coreflections create colimits, and every algebra is a colimit of a free algebra (see here).
-
When is the adjunction associated to the Kleisli category of a monad, is dense (a corollary of the pullback theorem) and fully faithful.
Related concepts
References
The initiality of the Kleisli category under monad morphisms was first observed in
- Jean-Marie Maranda, On Fundamental Constructions and Adjoint Functors, Canadian Mathematical Bulletin 9 5 (1966) 581-591 [doi:10.4153/CMB-1966-072-9]
Textbook account:
- Saunders MacLane, §VI.3 of: Categories for the Working Mathematician, Graduate Texts in Mathematics 5 Springer (1971) [doi:10.1007/978-1-4757-4721-8]
Last revised on September 22, 2023 at 06:21:16. See the history of this page for a list of all contributions to it.