nLab Kleisli category
Context
2-Category theory
Definitions
Transfors between 2-categories
Morphisms in 2-categories
Structures in 2-categories
Limits in 2-categories
Structures on 2-categories
Higher algebra
Algebraic theories
Algebras and modules
Higher algebras
-
symmetric monoidal (∞,1)-category of spectra
Model category presentations
Geometry on formal duals of algebras
Theorems
Kleisli category
Idea
Given a monad on some category , then its Kleisli category is the full subcategory of the Eilenberg-Moore category of , hence the category of T-algebras, on those that are free T-algebras (free -modules).
Explicitly one may describe (Prop. below) the Kleisli category of (Def. ) to have as objects the objects of , and a morphism in the Kleisli category is a morphism in of the form in . The monad structure induces a natural composition of such “-shifted” morphisms.
The Kleisli category is also characterized by the following universal property:
Since every adjunction gives rise to a monad on the domain of its left adjoint, we might ask if every monad may be construed as arising from an adjunction. This is in fact true, and the initial such adjunction in the category of adjunctions for the given monad has the Kleisli category as the codomain of its left adjoint.
Definition
Let be a monad in Cat, where is an endofunctor with
-
multiplication ,
-
unit.
In terms of free algebras
Definition
A free -algebra over a monad (or free -module) is a -algebra (module) of the form , where the action is the component of multiplication transformation .
Definition
The Kleisli category of the monad is the full subcategory of the Eilenberg-Moore category on the free -algebras (Def. ).
Remark
If is the forgetful functor and is the free algebra functor , then the Kleisli category is simply the full subcategory of containing those objects in the image of .
In terms of Kleisli morphisms
As another way of looking at this, we can keep the same objects as in but redefine the morphisms. This was the original Kleisli construction:
Definition
The Kleisli category of a monad on a category has:
-
as objects the objects of ,
-
as morphisms the morphisms of the form
(1)in , called Kleisli morphisms;
and
-
composition of with is given by the Kleisli composition rule
(2) -
the identity morphisms on is the Kleisli morphism which is the -unit .
Proposition
(Kleisli equivalence)
The construction which sends a Kleisli morphism (1) to
constitutes a fully faithful functor
from the -Kleisli category (Def. ) to the category of -algebras, hence constitutes an equivalence of categories onto its essential image (the free -algebras).
(eg. Borceux (1994), Prop. 4.1.6)
Proof
To see that the functor is full, hence that is surjective, oberve that any homomorphism of algebras is the image of , as shown by the following commuting diagram:
Here the triangle on the left is the unit law of the monad, while the commutativity of the square is the fact that is a homomorphism of algebras.
To see that the functor is faithful, hence that is injective, notice that
by naturality of the unit combined with its unit law:
whence
Remark
This Kleisli composition plays an important role in computer science; for this, see the article at monad (in computer science).
Two-sided Kleisli category
Proposition
If in addition to the given monad there is a comonad on the same category , equipped with a distributivity law (see there)
then there is a two-sided (“double”) Kleisli category whose objects are those of , and whose morphisms are morphisms in of the form
with two-sided Kelisli composition
given by the (co-)bind-operation on the factors connected by the distributivity transformation:
Proposition
In the situation of Prop. , given in addition:
-
another monad on
- also equipped with distributivity over the given comonad ,
-
- which is compatible with the distributive laws in that that
then the usual compatibility of the one-sided-Kleisli category under monad transformations (see here) passes to the two-sided Kleisli category, in that
Proof
Consider the following diagram:
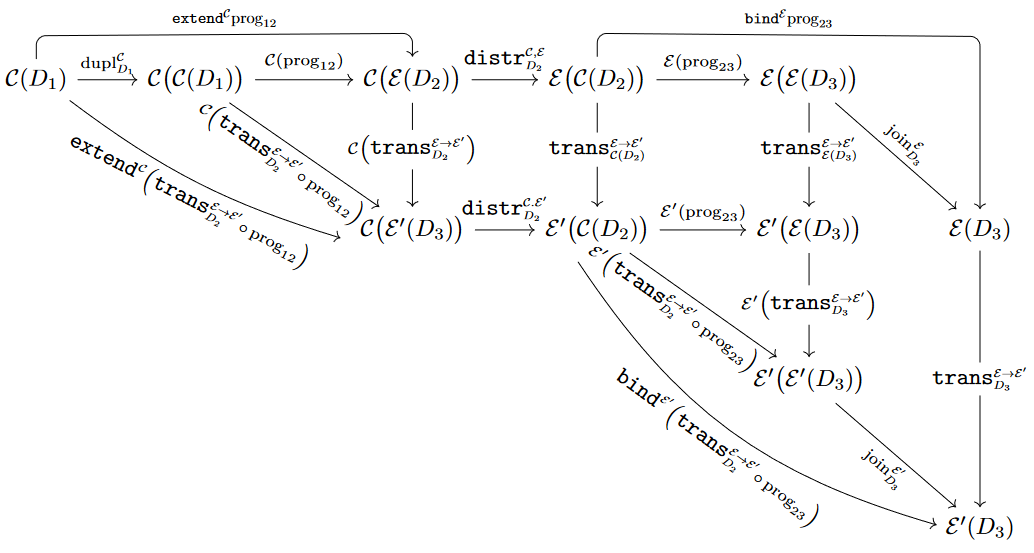
Here all squares commute by assumption on the monad transformation and hence the entire diagram commutes. Now the total top and right composite is the right hand side of (3), while the total left and bottom composite is the left hand side of (3), thus proving their equality.
Properties
Adjunction
Each Kleisli category comes with an adjunction
In terms of Kleisli morphisms:
- The functor is the identity on objects, and on morphisms it maps to the Kleisli morphism defined by , where is the unit of the monad.
- The functor maps an object to the object , and a Kleisli morphism defined by to its Kleisli extension , where is the multiplication of the monad.
In terms of free algebras:
- The functor maps an object to the free algebra , where is the multiplication of the monad, and a morphism to the morphism of algebras .
- The functor is the forgetful functor mapping free algebras and morphisms of algebras to the underlying objects and morphisms of .
Universal properties
In more general 2-categories the universal properties of Kleisli objects are dual to the universal properties of Eilenberg-Moore objects.
In particular, is initial in the category of adjunctions for (whereas is terminal). For a proof, see Category Theory in Context Proposition 5.2.12.
Limits and colimits
-
By the fact that the functor is left adjoint, it preserves all the colimits which exist in .
-
While , in general, doesn’t preserve all limits, one can say the following:
Proposition
A limit in is preserved by if and only if it is preserved by the monad .
Proof
Let be a diagram in , and suppose its limit exists.
First, suppose that the limit of is preserved by . Then since is right adjoint, it preserves limits, and so the limit of is also preserved by .
Conversely, denote by the forgetful functor from the Eilenberg-Moore category of , and denote by the comparison functor. We have that factors as , and so . Now suppose that the limit of is preserved by . Since is monadic and monadic functors create limits, the limit is also preserved by the functor . Now since is a full inclusion, and full inclusions reflect limits, the limit is also preserved by the functor alone.
Examples
General
Example
In typed functional programming, the Kleisli category is used to model call-by-value? functions with side effects and computation. Dually, the co-Kleisli category of a comonad may be used to model call-by-name? programming , see there.
Generally, see at monad (in computer science) for more on this.
Specific
Example
(matrix multiplication as (co-)Kleisli composition)
See here.
Related concepts
References
The original articles:
-
Heinrich Kleisli, Every standard construction is induced by a pair of adjoint functors, Proc. Amer. Math. Soc. 16, AMS (1965) 544-546 [ISSN0002-9939, jstor:2034693]
-
Jean-Marie Maranda, On Fundamental Constructions and Adjoint Functors, Canadian Mathematical Bulletin 9 5 (1966) 581-591 [doi:10.4153/CMB-1966-072-9]
Early accounts (together with the Eilenberg-Moore category):
-
Fred Linton, §7 in: An outline of functorial semantics, in Seminar on Triples and Categorical Homology Theory, Lecture Notes in Mathematics 80, Springer (1969) 7-52 [doi:10.1007/BFb0083080]
-
Saunders MacLane, §VI.5 of: Categories for the Working Mathematician, Graduate Texts in Mathematics 5 Springer (1971) [doi:10.1007/978-1-4757-4721-8]
-
Michael Barr, Charles Wells, §3.2 of: Toposes, Triples, and Theories, Grundlehren der math. Wissenschaften 278, Springer (1983) [TAC:12]
-
Jenö Szigeti, On limits and colimits in the Kleisli category, Cahiers de Topologie et Géométrie Différentielle Catégoriques 24 4 (1983) 381-391 [numdam:CTGDC_1983__24_4_381_0]
The equivalence of categories between the Kleisli category over a given monad with the co-Kleisli category of an adjoint comonad (if it exists):
- Mark Kleiner, Adjoint monads and an isomorphism of the Kleisli categories, Journal of Algebra 133 1 (1990) 79-82 [doi:10.1016/0021-8693(90)90069-Z]
The terminology “Kleisli triple” for a monad presented as an “extension system” and relation to computation with effects (see at monads in computer science):
- Eugenio Moggi, Notions of computation and monads, Information and Computation, 93 1 (1991) [doi:10.1016/0890-5401(91)90052-4, pdf]
Textbook account making explicit the Kleisli equivalence:
- Francis Borceux, pp. 191 in: Handbook of Categorical Algebra, Vol 2 Categories and Structures, Encyclopedia of Mathematics and its Applications 50, Cambridge University Press (1994) [doi:10.1017/CBO9780511525865]
Lecture notes:
- Thomas Streicher, pp. 54 in: Introduction to Category Theory and Categorical Logic (2003) [pdf, pdf]
Discussion of cases where the inclusion of the Kleisli category into the Eilenberg-Moore category is a reflective subcategory:
- Marcelo Fiore, Matias Menni, Reflective Kleisli subcategories of the category of Eilenberg-Moore algebras for factorization monads, Theory and Applications of Categories, Vol. 15, CT2004, No. 2, pp 40-65. (TAC)
Discussion of combined “double” or “two-sided” Kleisli categories, combining the Kleisli category of a monad with the co-Kleisli category of a comonad that distributes over it:
- Stephen Brookes, Kathryn Van Stone, Monads and Comonads in Intensional Semantics (1993) [dtic:ADA266522, pdf, pdf]
and generalization to 2-monads:
- Richard Garner, pp. 11 of: Polycategories via pseudo-distributive laws, Advances in Mathematics 218 3 (2008) 781-827 [arXiv:0606735, doi:10.1016/j.aim.2008.02.001]
Discussion in internal category theory:
- Tomasz Brzeziński, Adrian Vazquez-Marquez, Internal Kleisli categories, Journal of Pure and Applied Algebra 215 9 (2011) 213-147 [arXiv:0911.4048]
Discussion in a context of categorical systems theory:
- David Jaz Myers, §2.3 of: Categorical systems theory, book project [github, pdf]
Discussion of Kleisli categories in type theory is in
- Alex Simpson, Recursive types in Kleisli Categories (pdf)
Last revised on July 28, 2024 at 14:11:32. See the history of this page for a list of all contributions to it.