nLab logical conjunction
Context
-Category theory
Logical conjunction
Definitions
In logic, logical conjunction is the meet in the poset of truth values.
Assuming that (as in classical logic) the only truth values are true () and false (), then the conjunction of the truth values and may be defined by a truth table:
That is, is true if and only if and are both true. Conjunction also exists in nearly every non-classical logic.
More generally, if and are any two relations on the same domain, then we define their conjunction pointwise, thinking of a relation as a function to truth values. If instead we think of a relation as a subset of its domain, then conjunction becomes intersection.
Remarks
Conjunction is de Morgan dual to disjunction.
Like any meet, conjunction is an associative operation, so we can take the conjunction of any finite positive whole number of truth values; the conjunction is true if and only if all of the individual truth values are true. Conjunction also has an identity element, which is the true truth value. Some logics allow a notion of infinitary conjunction. Indexed conjunction is universal quantification.
As truth values form a poset, which is a degenerate kind of category, so truth values under conjunction form a meet-semilattice, which is a degenerate kind of cartesian monoidal category. Self-referentially, a poset is (up to equivalence) simply a category enriched over the cartesian monoidal category of truth values. With implication as internal hom, truth values form a closed cartesian category.
In the context of substructural logics such as linear logic, the conjunction defined above is also called additive conjunction to disambiguate it from the multiplicative conjunction.
Rules of inference
That conjunction is a meet means that may be proved in a context if and only if both and may be proved in . This directly yields the introduction and elimination rules for conjunction in natural deduction:
Alternatively, we may use these slightly more complicated (but fewer) inductive forms:
In sequent calculus, the same ideas become these rules:
Equivalently, we can use the following rules with weakened contexts:
The rules above are written so as to remain valid in logics without the exchange rule. In linear logic, the first batch of sequent rules apply to additive conjunction (interpret in these rules as ), while the second batch of rules apply to multiplicative conjunction (interpret in those rules as ).
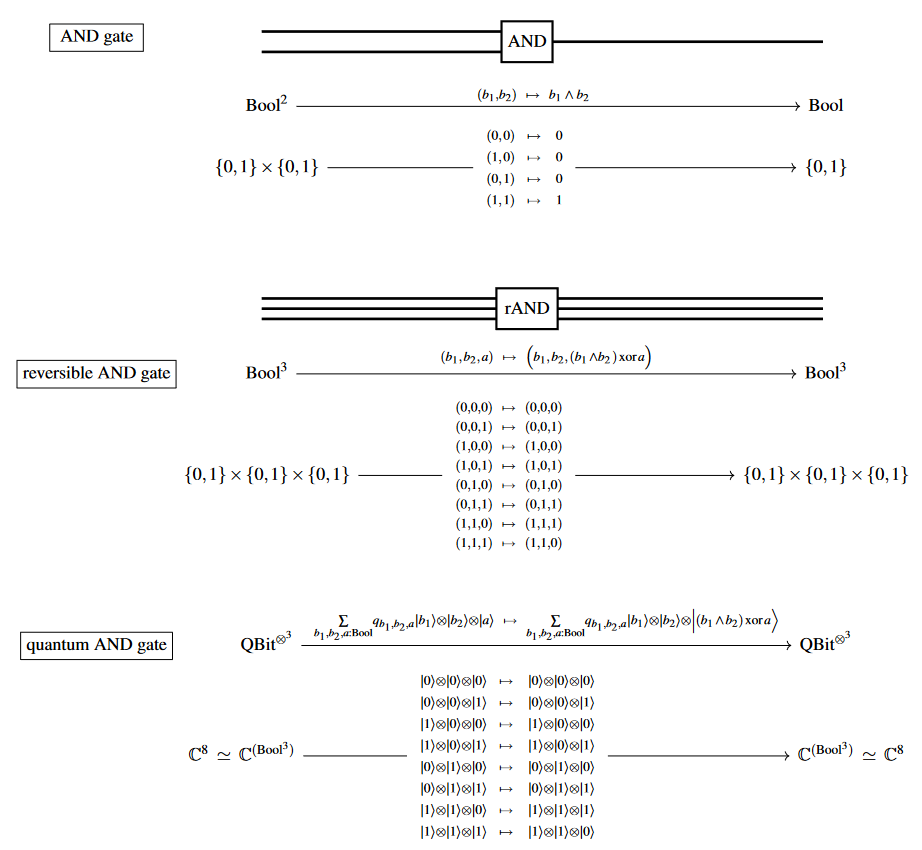
As a logic gate
Logical conjunction as
-
a logic gate,
-
a reversible logic gate and
-
a (reversible) quantum logic gate:
Related concepts
Last revised on March 29, 2023 at 10:24:04. See the history of this page for a list of all contributions to it.