nLab logical conjunction

Definitions

In logic, logical conjunction is the meet in the poset of truth values.

Assuming that (as in classical logic) the only truth values are true ($T$) and false ($F$), then the conjunction $p \wedge q$ of the truth values $p$ and $q$ may be defined by a truth table:

$p$	$q$		$p \wedge q$
$T$	$T$		$T$
$T$	$F$		$F$
$F$	$T$		$F$
$F$	$F$		$F$

That is, $p \wedge q$ is true if and only if $p$ and $q$ are both true. Conjunction also exists in nearly every non-classical logic.

More generally, if $p$ and $q$ are any two relations on the same domain, then we define their conjunction pointwise, thinking of a relation as a function to truth values. If instead we think of a relation as a subset of its domain, then conjunction becomes intersection.

Remarks

Conjunction is de Morgan dual to disjunction.

Like any meet, conjunction is an associative operation, so we can take the conjunction of any finite positive whole number of truth values; the conjunction is true if and only if all of the individual truth values are true. Conjunction also has an identity element, which is the true truth value. Some logics allow a notion of infinitary conjunction. Indexed conjunction is universal quantification.

As truth values form a poset, which is a degenerate kind of category, so truth values under conjunction form a meet-semilattice, which is a degenerate kind of cartesian monoidal category. Self-referentially, a poset is (up to equivalence) simply a category enriched over the cartesian monoidal category of truth values. With implication as internal hom, truth values form a closed cartesian category.

In the context of substructural logics such as linear logic, the conjunction defined above is also called additive conjunction to disambiguate it from the multiplicative conjunction.

Rules of inference

That conjunction is a meet means that $p \wedge q$ may be proved in a context $\Gamma$ if and only if both $p$ and $q$ may be proved in $\Gamma$. This directly yields the introduction and elimination rules for conjunction in natural deduction:

$$\begin {gathered} \frac { \Gamma \vdash p ; \; \Gamma \vdash q } { \Gamma \vdash p \wedge q } \; \text {introduction} \\ \frac { \Gamma \vdash p \wedge q } { \Gamma \vdash p } \; \text {elimination 0} \\ \frac { \Gamma \vdash p \wedge q } { \Gamma \vdash q } \; \text {elimination 1} \\ \end {gathered}$$

Alternatively, we may use these slightly more complicated (but fewer) inductive forms:

$$\begin {gathered} \frac { \Gamma \vdash p ; \; \Gamma \vdash q } { \Gamma \vdash p \wedge q } \; \text {introduction} \\ \frac { \Gamma , p , q \vdash r } { \Gamma , p \wedge q , \vdash r } \; \text {elimination} \\ \end {gathered}$$

In sequent calculus, the same ideas become these rules:

$$\begin {gathered} \frac { \Gamma \vdash \Delta , p , \Sigma ; \; \Gamma \vdash \Delta , q , \Sigma } { \Gamma \vdash \Delta , p \wedge q , \Sigma } \; \text {right additive} \\ \frac { \Gamma , p , \Delta \vdash \Sigma } { \Gamma , p \wedge q , \Delta \vdash \Sigma } \; \text {left additive 0} \\ \frac { \Gamma , q , \Delta \vdash \Sigma } { \Gamma , p \wedge q , \Delta \vdash \Sigma } \; \text {left additive 1} \\ \end {gathered}$$

Equivalently, we can use the following rules with weakened contexts:

$$\begin {gathered} \frac { \Gamma \vdash \Delta , p ; \; \Sigma \vdash q , \Pi } { \Gamma , \Sigma \vdash \Delta , p \wedge q , \Pi } \; \text {right multiplicative} \\ \frac { \Gamma , p , q , \Delta \vdash \Sigma } { \Gamma , p \wedge q , \Delta \vdash \Sigma } \text {left multiplicative} \\ \end {gathered}$$

The rules above are written so as to remain valid in logics without the exchange rule. In linear logic, the first batch of sequent rules apply to additive conjunction (interpret $p \wedge q$ in these rules as $p \& q$), while the second batch of rules apply to multiplicative conjunction (interpret $p \wedge q$ in those rules as $p \otimes q$).

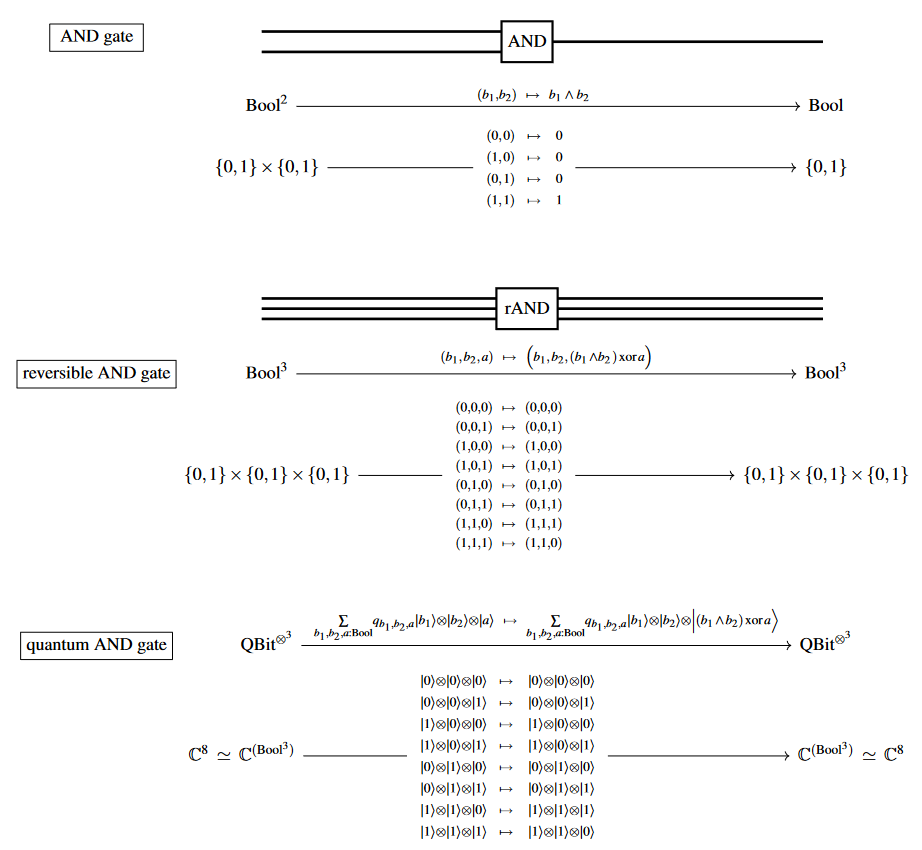
As a logic gate

Logical conjunction as

1. a logic gate,

2. a reversible logic gate and

3. a (reversible) quantum logic gate:

Related concepts

• in linear logic: multiplicative conjunction

$\phantom{-}$symbol$\phantom{-}$	$\phantom{-}$in logic$\phantom{-}$
$\phantom{A}$$\in$	$\phantom{A}$element relation
$\phantom{A}$$\,:$	$\phantom{A}$typing relation
$\phantom{A}$$=$	$\phantom{A}$equality
$\phantom{A}$$\vdash$$\phantom{A}$	$\phantom{A}$entailment / sequent$\phantom{A}$
$\phantom{A}$$\top$$\phantom{A}$	$\phantom{A}$true / top$\phantom{A}$
$\phantom{A}$$\bot$$\phantom{A}$	$\phantom{A}$false / bottom$\phantom{A}$
$\phantom{A}$$\Rightarrow$	$\phantom{A}$implication
$\phantom{A}$$\Leftrightarrow$	$\phantom{A}$logical equivalence
$\phantom{A}$$\not$	$\phantom{A}$negation
$\phantom{A}$$\neq$	$\phantom{A}$negation of equality / apartness$\phantom{A}$
$\phantom{A}$$\notin$	$\phantom{A}$negation of element relation $\phantom{A}$
$\phantom{A}$$\not \not$	$\phantom{A}$negation of negation$\phantom{A}$
$\phantom{A}$$\exists$	$\phantom{A}$existential quantification$\phantom{A}$
$\phantom{A}$$\forall$	$\phantom{A}$universal quantification$\phantom{A}$
$\phantom{A}$$\wedge$	$\phantom{A}$logical conjunction
$\phantom{A}$$\vee$	$\phantom{A}$logical disjunction
symbol	in type theory (propositions as types)
$\phantom{A}$$\to$	$\phantom{A}$function type (implication)
$\phantom{A}$$\times$	$\phantom{A}$product type (conjunction)
$\phantom{A}$$+$	$\phantom{A}$sum type (disjunction)
$\phantom{A}$$0$	$\phantom{A}$empty type (false)
$\phantom{A}$$1$	$\phantom{A}$unit type (true)
$\phantom{A}$$=$	$\phantom{A}$identity type (equality)
$\phantom{A}$$\simeq$	$\phantom{A}$equivalence of types (logical equivalence)
$\phantom{A}$$\sum$	$\phantom{A}$dependent sum type (existential quantifier)
$\phantom{A}$$\prod$	$\phantom{A}$dependent product type (universal quantifier)
symbol	in linear logic
$\phantom{A}$$\multimap$$\phantom{A}$	$\phantom{A}$linear implication$\phantom{A}$
$\phantom{A}$$\otimes$$\phantom{A}$	$\phantom{A}$multiplicative conjunction$\phantom{A}$
$\phantom{A}$$\oplus$$\phantom{A}$	$\phantom{A}$additive disjunction$\phantom{A}$
$\phantom{A}$$\&$$\phantom{A}$	$\phantom{A}$additive conjunction$\phantom{A}$
$\phantom{A}$$\invamp$$\phantom{A}$	$\phantom{A}$multiplicative disjunction$\phantom{A}$
$\phantom{A}$$\;!$$\phantom{A}$	$\phantom{A}$exponential conjunction$\phantom{A}$
$\phantom{A}$$\;?$$\phantom{A}$	$\phantom{A}$exponential disjunction$\phantom{A}$