nLab pushout-product

Idea

The concept of pushout product is a natural kind of pairing operation on morphisms in categories equipped with a pairing operation on objects (e.g. a tensor product) and having pushouts. It sends two morphisms to the universal morphism out of the pushout of the span-diagram they form by pairing their domain objects. Regarding arrows in a category as diagrams with domain the interval category, and giving the interval category the natural monoidal product, this is a kind of Day convolution tensor product with the natural copowering over Set replacing a tensor in the coend.

Definition

Consider

• three categories $\mathcal{E}_i$, $i \in \{1,2,3\}$

  (often taken to be the same),

• a functor $\otimes \colon \mathcal{E}_1 \times \mathcal{E}_2 \to \mathcal{E}_3$ out of the product category

  (often being the tensor product on a monoidal category or the tensoring of an enriched category over its cosmos).

Assume that $\mathcal{E}_3$ has all pushouts.

Definition

Given a pair of morphisms

• $f \colon A \to B$ in $\mathcal{E}_1$

• $g \colon X \to Y$ in $\mathcal{E}_2$,

their pushout product is the morphism in $\mathcal{E}_3$

$$f \,\widehat{\otimes}\, g \;\;\colon\;\; A \otimes Y \overset {A \otimes X} {\amalg} B \otimes X \longrightarrow B \otimes Y$$

out of the pushout of the two morphisms, which is induced by the universal property of the pushout by the following commuting diagram (induced, in turn, from the functoriality of the tensor product as a functor on a product category):

$$\array{ A \otimes X &\overset{f \otimes id_X}{\longrightarrow}& B \otimes X \\ \mathllap{{}^{id_A \otimes g}}\Big\downarrow && \Big\downarrow\mathrlap{{}^{id_B \otimes g}} \\ A \otimes Y &\underset{f \otimes id_Y}{\longrightarrow}& B \otimes Y \mathrlap{\,.} }$$

The pushout product defines a functor ${\widehat{\otimes}} \colon \mathcal{E}_1^{\mathbf{2}} \times \mathcal{E}_2^{\mathbf{2}} \to \mathcal{E}_3^{\mathbf{2}}$ on arrow categories with the evident functorial action.

Properties

The pushout product associated to ${\otimes} \colon \mathcal{E}_1 \times \mathcal{E}_2 \to \mathcal{E}_3$ inherits various properties from $\otimes$ (see Riehl & Verity (2014)):

Proposition

Let $\mathcal{E}$ be a category with pushouts and let $\otimes \colon \mathcal{E} \times \mathcal{E} \to \mathcal{E}$ be a functor equipped with a natural isomorphism $(A \otimes B) \otimes C \cong A \otimes (B \otimes C)$. Then we have a natural isomorphism $(f \,\widehat{\otimes}\, g) \,\widehat{\otimes}\, h \cong f \,\widehat{\otimes}\, (g \,\widehat{\otimes}\, h)$.

Proposition

Let $\mathcal{E}_1,\mathcal{E}_2,\mathcal{E}_3$ be categories such that $\mathcal{E}_3$ has pushouts and let $\otimes \colon \mathcal{E}_1 \times \mathcal{E}_2 \to \mathcal{E}_3$. If $\otimes$ is cocontinuous? in its first (resp. second) argument, then so is $\widehat{\otimes}$.

Proof

(Riehl & Verity 2014, Lemma 4.8)

The following related property is also observed at Joyal-Tierney calculus.

Proposition

Let $\mathcal{E}_1,\mathcal{E}_2,\mathcal{E}_3$ be categories such that $\mathcal{E}_2$ has pullbacks and $\mathcal{E}_3$ has pushouts. Let $\otimes \colon \mathcal{E}_1 \times \mathcal{E}_2 \to \mathcal{E}_3$ and $hom_r(-,-) \colon \mathcal{E}_1^{op} \times \mathcal{E}_3 \to \mathcal{E}_2$ such that $A \otimes (-)$ is left adjoint to $hom_r(A,-)$ for all $A \in \mathcal{E}_1$. Write $\widehat{hom}_r \colon (\mathcal{E}_1^{\mathbf{2}})^{op} \times \mathcal{E}_3^{\mathbf{2}} \to \mathcal{E}_2^{\mathbf{2}}$ for the pushout product associated to $hom_r(-,-)^{op} \colon \mathcal{E}_1 \times \mathcal{E}_3^{op} \to \mathcal{E}_2^{op}$ (i.e. the pullback power). Then $f \,\widehat{\otimes}\, (-) \colon \mathcal{E}_2^{\mathbf{2}} \to \mathcal{E}_3^{\mathbf{2}}$ is left adjoint to $\widehat{hom}_r(f,-) \colon \mathcal{E}_3^{\mathbf{2}} \to \mathcal{E}_2^{\mathbf{2}}$ for all $f \in \mathcal{E}_1^{\mathbf{2}}$.

Proof

(Riehl & Verity 2014, Lemma 4.10)

For $\mathcal{C}$ any category and $K\subset Mor(\mathcal{C})$ any class of its morphisms, write $K Inj$ for the $K$-injective morphisms and $K Cof \coloneqq (K Inj)Proj$ for the $K Inj$-projective morphisms.

Proposition

Let $\mathcal{C}$ be a symmetric closed monoidal category with finite limits and finite colimits, and let $I_1, I_2\subset Mor(\mathcal{C})$ be two classes of its morphisms.

Then under pushout product $\widehat{\otimes}$:

$$(I_1 Cof) \,\widehat{\otimes}\, (I_2 Cof) \subset (I_1 \,\widehat{\otimes}\, I_2) Cof \,.$$

(Hovey-Shipley-Smith 00, Proposition 5.3.4)

Proof

By a little Joyal-Tierney calculus.

Remark

In the context of monoidal model category theory, prop. implies that for checking the pushout-product axiom in the case of cofibrantly generated model categories it is sufficient to check it on generating cofibrations.

Examples

In Sets

It is instructive to consider the elementary case of pushout-products in Sets with respect to the Cartesian product

$$\times \;\colon\; Set \times Set \longrightarrow Set \,.$$

For a pair of maps/functions of sets

$$\array{ f \; \colon & X &\longrightarrow& X' \\ g \; \colon & Y &\longrightarrow& Y' }$$

the relevant pushout diagram is

where the dashed arrow denotes the pushout-product map.

Example

The pushout-product of sets may be described as the quotient set

$$f \,\widehat{\times}\, g \;\; \simeq \;\; \big\{ (x,y'), \, (x',y) \big\}_{ \bigg/ \Big( \big(x,\,g(y)\big) \,\sim\, \big(f(x),\,y\big) \Big) }$$

(where each variable ranges over the set denoted by the corresponding capital symbol).

Moreover, if we denote the equivalence class of $(x,y')$ by $[x,y']$, etc. then the coprojections into the pushout product are given by

$$\array{ X' \times Y &\xrightarrow{\;\; q_l\;\;}& f \,\widehat{\times}\, g \\ (x',\,y) &\mapsto& [x',\, y] } \;\;\;\;\;\;\;\;\; \text{and} \;\;\;\;\;\;\;\;\; \array{ X \times Y' &\xrightarrow{\;\; q_r\;\;}& f \,\widehat{\times}\, g \\ (x,\,y') &\mapsto& [x,\, y'] }$$

and the pushout-product map itself (the dashed arrow) is given as follows:

(1)$$\array{ f \,\widehat{\times}\, g &\xrightarrow{\phantom{---}}& X' \times Y' \\ [x',\, y] &\mapsto& \big(x',\, g(y)\big) \\ [x,\, y'] &\mapsto& \big(f(x),\, y' \big) \mathrlap{\,.} }$$

More informatively, the fibers of the pushout-product map over any $(x',y') \,\in\, X' \times Y'$ look as follows:

(2)$$\big( f \,\widehat{\times}\, g \big)_{(x',y')} \;\; = \;\; \left\{ \array{ \ast &\vert& (x',y') \;\in\; im(f) \times im(g) \\ f^{-1}\big(\{x'\}\big) &\vert& y' \;\in\; Y' \setminus im(g) \\ g^{-1}\big(\{y'\}\big) &\vert& x' \;\in\; X' \setminus im(f) } \right.$$

where

• “$\ast$” denotes the singleton set

• “$(-)^{-1}$” denotes forming preimages

• “$\setminus$” denotes forming complements.

Proof

We discuss in more detail how to obtain the fibers (2).

To see the first case: By the assumption that $x' \,\in\, im(f)$ we find $x_1 \in f^{-1}\big(\{x'\}\big)$ and hence by (1) we find $[x_1,y'] \,\in\, \big(f \,\widehat{\times}\, g\big)_{(x',y')}$. But since also $y' \,\in\, im(g)$ there is also $y \in g^{-1}\big(\{y'\}\big)$ and hence

$$\big[x_1,\, y'\big] \,=\, \big[x_1,\, g(y)\big] \,=\, \big[f(x_1),\, y\big] \,=\, \big[x',\, y\big] \,.$$

This shows that all elements of the form $[x,y']$ in the fiber are in fact equal, and also equal to $[x', y]$, which, by the symmetric argument, are in turn equal for all choices of $y$. Therefore there is one single element in the fiber of the pushout-product map, in this case.

To see the second case: Since $y'$ is not in the image of $g$, by (1) the elements in the fiber can only be of the form $[x,y']$ with $x \in f^{-1}\big(\{x'\}\big)$. None of these is contained in the relation – again by the assumption that $y'$ is not in the image of $g$ – and hence they are all distinct.

The third case works the same way, under swapping $X \leftrightarrow Y$.

Example

(Pushout-product of injections of sets)
In the special case that both maps are injections, the fibers appearing in (2) are all (-1)-truncated (either empty sets or singleton sets).

This shows that the pushout-product map of two injections of Sets is itself an injection. The following graphics illustrates this for interval-subsets of the plane:

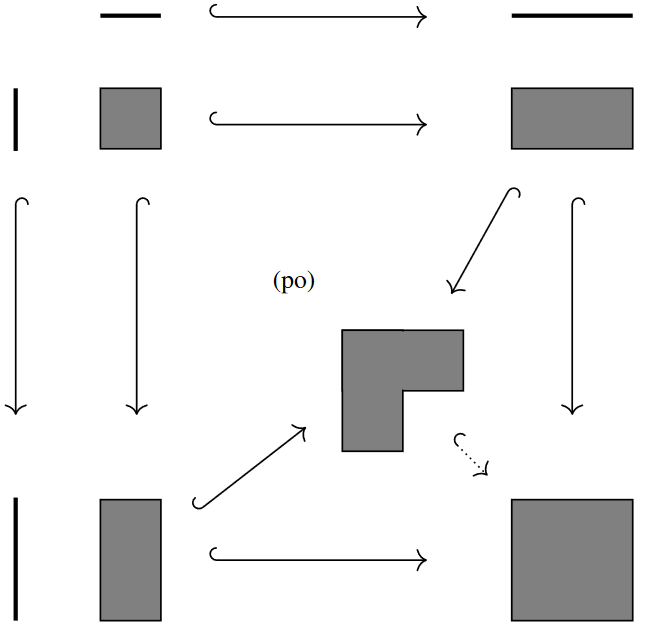
In Topological Spaces

Example

For $n \in \mathbb{N}$, let

$$i_n \;\colon\; S^{n-1}\hookrightarrow D^n$$

be the canonical sphere inclusions in Top (the generating cofibrations of the classical model structure on topological spaces). Their pushout product (with respect to cartesian product of topological spaces) is given by addition of indices:

$$i_{n_1} \,\widehat{\times}\, i_{n_2} \simeq i_{n_1 + n_2} \,.$$

Let moreover

$$j_n \coloneqq (id,\delta_0) \;\colon\; D^n \hookrightarrow D^n \times I \,.$$

Then

$$i_{n_1} \,\widehat{\times}\, j_{n_2} \simeq j_{n_1 + n_2} \,.$$

Proof

To see this, it is profitable to model n-disks and n-spheres, up to homeomorphism, as n-cubes and their boundaries.

To see the idea of the proof, consider the situation in low dimensions, where one readily sees that

$$i_1 \,\widehat{\times}\, i_1 \;\colon\; (\; = \;\cup\; \vert\vert\;) \hookrightarrow \Box$$

and

$$i_1 \,\widehat{\times}\, j_0 \;\colon\; (\; = \;\cup\; \vert \; ) \hookrightarrow \Box \,.$$

Generally, $D^n$ may be represented as the space of $n$-tuples of elements in $[0,1]$, and $S^n$ as the suspace of tuples for which at least one of the coordinates is equal to 0 or to 1.

Accordingly $S^{n_1} \times D^{n_2}$ is the spaces of $(n_1+n_2)$-tuples, such that one of the first $n_1$ coordinates is equal to 0 or 1, and hence

$$S^{n_1} \times D^{n_2} \;\cup\; D^{n_1} \times S^{n_2} \;\;\simeq\;\; S^{n_1 + n_2} \,.$$

And of course it is clear that $D^{n_1} \times D^{n_2} \simeq D^{n_1 + n_2}$. This shows the first case.

For the second, use that $S^{n_1} \times D^{n_2} \times I$ is contractible to $S^{n_1} \times D^{n_2}$ in $D^{n_1} \times D^{n_2} \times I$, and that $S^{n_1} \times D^{n_2}$ is a subspace of $D^{n_1} \times D^{n_2}$.

Remark

The relations in example are the key in proving that the classical model structure on topological spaces (on compactly generated topological spaces) is an enriched model category over itself. See there at topological enrichment for more.

Pushout application of natural transformations

The following example exploits the generality of allowing $\mathcal{E}_1,\mathcal{E}_2,\mathcal{E}_3$ to differ in the functor $\otimes \colon \mathcal{E}_1 \times \mathcal{E}_2 \to \mathcal{E}_3$.

Let $\mathcal{C},\mathcal{D}$ be categories such that $\mathcal{D}$ has pushouts. We have the evaluation functor $ev \colon [\mathcal{C},\mathcal{D}] \times \mathcal{C} \to \mathcal{D}$ sending a functor $F$ and object $c$ to $F(d)$.

The induced pushout product $\widehat{ev} \colon [\mathcal{C},\mathcal{D}]^{\mathbf{2}} \times \mathcal{C}^{\mathbf{2}} \to \mathcal{D}^{\mathbf{2}}$ takes a natural transformation and a morphism of $\mathcal{C}$ and outputs a morphism of $\mathcal{D}$.

Example

Given a cylinder functor $C \colon \mathcal{E} \to \mathcal{E}$ with natural transformations $e_0,e_1 \colon Id_{\mathcal{E}} \to C$, the pushout application of $e_k$ to $f \colon A \to B$ is the map

$$B \amalg_A CA \overset{\widehat{ev}(e_k,f)}{\longrightarrow} CB$$

from the ($k$-oriented) mapping cylinder of $f$ to the cylinder on $B$.

Now suppose additionally that $\mathcal{C}$ has pullbacks. Write $Cat_adj(\mathcal{C},\mathcal{D})$ for the category whose objects are adjoint functors $\mathcal{C} : L \dashv R : \mathcal{D}$ and whose morphisms are conjugate transformations of adjoints (in the direction of the transformation of left adjoints).

We have a functor $ev_L \colon Cat_adj(\mathcal{C},\mathcal{D}) \times \mathcal{C} \to \mathcal{D}$ which applies the left adjoint and a functor $ev_R \colon \Cat_adj(\mathcal{C},\mathcal{D})^{op} \times \mathcal{D} \to \mathcal{C}$ which applies the right adjoint, and $ev_L(L \dashv R, -)$ is left adjoint to $ev_R(L \dashv R, -)$ for every pair of adjoints $L \dashv R$.

Hence for any conjugate transformations $(\lambda, \rho) \colon (L_1 \dashv R_1) \to (L_2 \dashv R_2)$, it follows from Proposition that the pushout product $\widehat{ev_L}((\lambda, \rho),-)$ (which is the same as $\widehat{ev}(\lambda,-)$) is left adjoint to the pullback power $\widehat{ev_R}((\lambda,\rho),-)$.

Example

Given a cylinder functor $C \colon \mathcal{E} \to \mathcal{E}$ with a right adjoint $P \colon \mathcal{E} \to \mathcal{E}$, the conjugates of $e_0,e_1 \colon Id_{\mathcal{E}} \to C$ make $P$ into a functorial cocylinder. The pushout application of $e_k$ from Example is then left adjoint to the pullback application of its conjugate, which sends $f : Y \to X$ to the map $P Y \to Y \times_X P X$ from the path space of $Y$ to the mapping path space of $f$.

General

Example

(pushout-product with initial morphism is tensor product)
With respect to a bifunctor $\otimes \;\colon\; \mathcal{C} \times \mathcal{C} \longrightarrow \mathcal{C}$ which preserves initial objects $\varnothing$ in, say, the first variable, the pushout-product with an initial morphisms $\varnothing \to X$ is given by $X \otimes (-)$:

$$\big( \varnothing \to X \big) \,\widehat{\otimes}\, g \;\simeq\; id_X \otimes g \,.$$

(Of course, in applications $(-)\otimes(-)$ is typically a closed tensor product which hence even preserves all colimits in each variable separately.)

This is because the defining pushout diagram now looks like this:

where the top row is the unique map on the initial object by assumption whence its pushout to the bottom horizontal morphism is also an identity, as shown.

Example

(pushout product with identity is identity morphism)
With respect to any bifunctor $\otimes \,\colon\, \mathcal{C} \times \mathcal{C} \to \mathcal{C}$, the pushout-product with with an identity morphism is an identity morphism:

$$f \,\widehat{\otimes}\, id \;\simeq\; id \;\;\;\;\;\;\;\;\; \text{and} \;\;\;\;\;\;\;\;\; id \,\widehat{\otimes}\, g \;\simeq\; id \,.$$

This is because the defining pushout-diagram, say in the first case, now looks like this: because the top morphism is an identity morphism by assumption, so that also its pushout is given by an identity, as shown.

The analogous argument applies in the other variable.

Example

With respect to any bifunctor $\otimes \;\colon\; \mathcal{C} \times \mathcal{C} \longrightarrow \mathcal{C}$ the pushout-product of two split epimorphisms

$$\array{ f \,\colon & X &\overset{split}{\twoheadrightarrow}& X' \\ g \,\colon & Y &\overset{split}{\twoheadrightarrow}& Y' }$$

is an isomorphism, in that the following commuting square is already a pushout

$$\array{ X \otimes Y &\overset{id \times g}{\longrightarrow}& X \otimes Y' \\ \mathllap{{}^{f \otimes id}} \Big\downarrow && \Big\downarrow \mathrlap{{}^{ f \otimes id}} \\ X' \otimes Y &\underset{id \otimes g}{\longrightarrow}& X' \otimes Y' \mathrlap{\,.} }$$

Proof

Given any cocone under the given span, such as shown in the outer part of the following diagram we need to see that there is a unique dashed morphism $\phi$ making the diagram commute, as shown.

Now, by assumption, we have sections

$$\array{ \overline{f} \,\colon & X' &\overset{\phantom{--}}{\hookrightarrow}& X & \text{with} & f \circ \overline{f} \,=\, id \\ \overline{g} \,\colon & Y' &\overset{\phantom{--}}{\hookrightarrow}& Y & \text{with} & g \circ \overline{g} \,=\, id }$$

from which we obtain a candidate dashed morphism by setting:

$$\begin{array}{l} \mathllap{ \phi \; \coloneqq \; } r \circ (\overline{f} \otimes id) \\ \;=\; r \circ (\overline{f} \otimes id) \circ (id \otimes g) \circ (id \otimes \overline{g}) \\ \;=\; r \circ (id \otimes g) \circ (\overline{f} \otimes id) \circ (id \otimes \overline{g}) \\ \;=\; s \circ (f \otimes id) \circ (\overline{f} \otimes id) \circ (id \otimes \overline{g}) \\ \;=\; s \circ (id \otimes \overline{g}) \,. \end{array}$$

This does make the bottom triangle commute

$$\begin{array}{l} \phi \circ (id \otimes g) \\ \;=\; r \circ (\overline{f} \otimes id) \circ (id \otimes g) \\ \;=\; r \circ (id \otimes g) \circ (\overline{f} \otimes id) \\ \;=\; s \circ (f \otimes id) \circ (\overline{f} \otimes id) \\ \;=\; s \end{array}$$

and analogously for the right triangle

$$\begin{array}{l} \phi \circ (f \otimes id) \\ \;=\; s \circ (id \otimes \overline{g}) \circ (f \otimes id) \\ \;=\; s \circ (f \otimes id) \circ (id \otimes \overline{g}) \\ \;=\; r \circ (id \otimes g) \circ (id \otimes \overline{g}) \\ \;=\; r \,; \end{array}$$

and given any $\phi$ making the diagram commute, we find that it equals the previous one:

$$\begin{array}{l} \phi \\ \;=\; \phi \circ (f \otimes id) \circ (\overline{f} \otimes id) \\ \;=\; r \circ (\overline{f} \otimes id) \,. \end{array}$$

Related concepts

• pullback power– the dual concept

• pushout-product axiom

• Joyal-Tierney calculus

References

Pushout-products are prominently discussed in the context of monoidal model category-theory (where they appear in a pushout-product axiom), and here a key motivation are constructions of symmetric monoidal smash products of spectra. See for instance:

• Mark Hovey, Brooke Shipley, Jeff Smith, Symmetric spectra, J. Amer. Math. Soc. 13 (2000), 149-208 (arXiv:math/9801077)

General properties of the pushout product are described in Sections 4 and 5 of

• Emily Riehl, Dominic Verity, The theory and practice of Reedy categories, Theory and Applications of Categories 29(9) (2014) 256–301 [tac,arXiv:1304.6871]

where the definition of $\widehat{\otimes}$ from $\otimes$ is called the Leibniz construction.