nLab trace of horizontal to round chord diagrams
Context
Knot theory
Examples/classes:
Types
Related concepts:
Contents
Idea
In knot theory, a certain trace-like operation turns horizontal chord diagrams into round chord diagrams:
Given a horizontal chord diagram on strands and given any choice of cyclic permutation of elements, the trace is the round chord diagram obtained by gluing the ends of the strands according to the cyclic permutation, and retaining the chords in the evident way.
The following graphics shows basic examples of the trace operation for cyclic permutation of strands one step to the right:
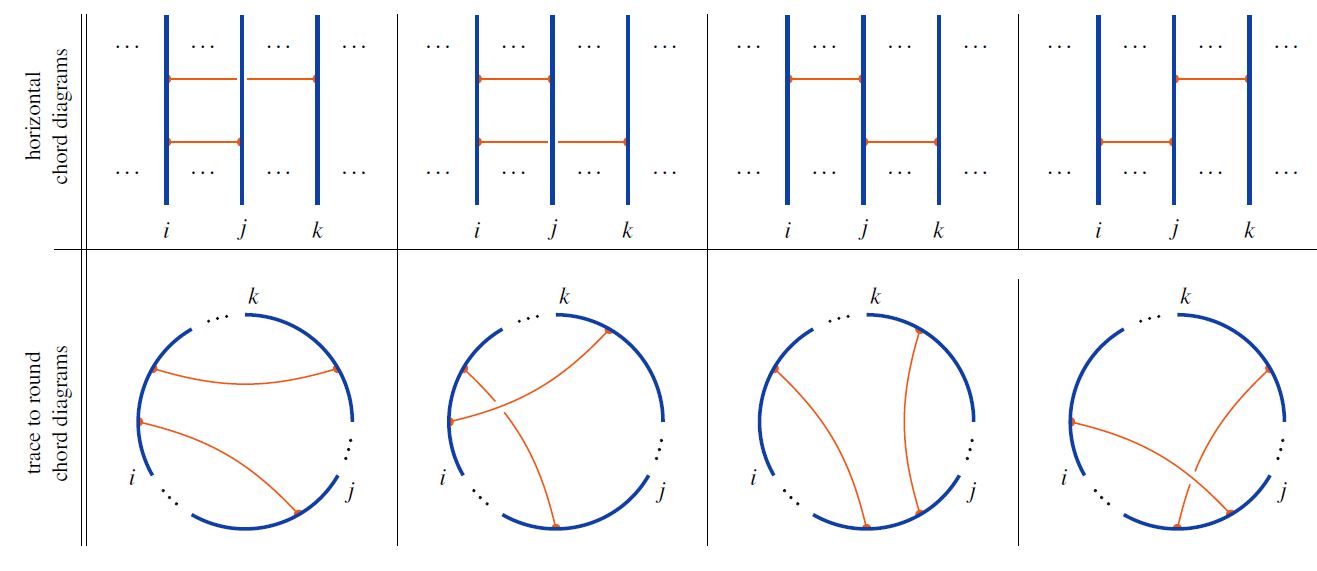
Properties
Relation to 4T relations
The trace operation sends the 4T relations on horizontal chord diagrams to those for round chord diagrams:
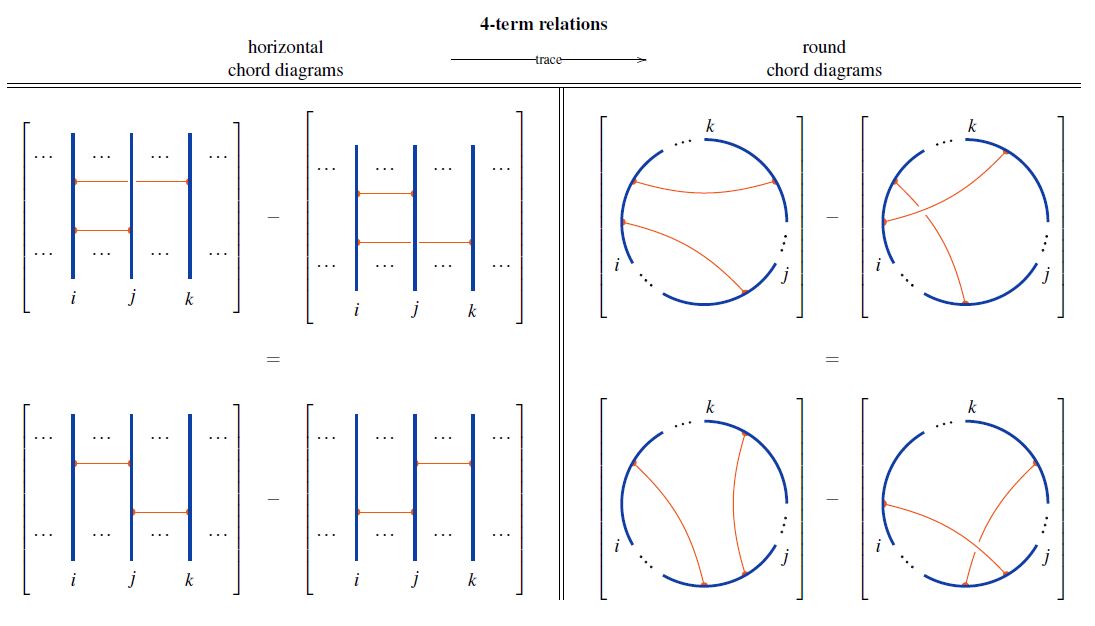
References
The trace operation is implicit in
- Dror Bar-Natan, Vassiliev and Quantum Invariants of Braids, Geom. Topol. Monogr. 4 (2002) 143-160 (arxiv:q-alg/9607001)
It is made a little more explicit in
- Toshitake Kohno, around Figure 2 of: Loop spaces of configuration spaces and finite type invariants, Geom. Topol. Monogr. 4 (2002) 143-160 (arXiv:math/0211056)
Created on November 28, 2019 at 07:47:05. See the history of this page for a list of all contributions to it.