nLab volume conjecture
Context
Manifolds and cobordisms
manifolds and cobordisms
cobordism theory, Introduction
Definitions
Genera and invariants
Classification
Theorems
Functorial quantum field theory
Contents
Idea
The volume conjectures are a class of conjectures (slightly differing in generality and assumptions), saying that on a suitable (in particular: hyperbolic) 3-manifold a large N limit of SU(n)-Chern-Simons theory quantum observables (-colored Jones polynomials or more generally RT-invariants, TV-invariants) is equal to the volume or complex volume of .
For a few special cases of 3-manifolds there are explicit proofs of the volume conjecture(s). Besides this there is an abundance of numerical evidence for the volume conjectures, using computer algebra such as SnapPy (see also Zickert 07). In fact experimentation with these numerics is what has been driving the formulation of further variants of the volume conjecture.
Hence experimental mathematics strongly suggests that the volume conjectures are true. But a conceptual explanation (let alone proof) in terms of quantum field theory has remained open (Witten 14, bottom of p. 4).
But an explanation via duality in string theory, combining AdS/CFT duality with the 3d/3d correspondence for wrapped M5-branes, is argued for in Gang-Kim-Lee 14, 3.2, Gang-Kim 18 (21), see below.
For on knot complements
The original volume conjecture (also “Kashaev’s conjecture”, due to Kashaev 95, and understood in terms of the -colored Jones polynomial by Murakami-Murakami 01) states that the large N limit of the -colored Jones polynomial (for gauge group SU(2)) of a knot gives the simplicial volume of its complement in the 3-sphere (for hyperbolic knots this is the volume of the complementary hyperbolic 3-manifold)
Here is the ratio of the values of the -colored Jones polynomial of and of the unknot
The simplicial volume of a knot complement can be found via its unique torus decomposition into hyperbolic pieces and Seifert fibered pieces by a system of tori. The simplicial volume is then the sum of the hyperbolic volumes of the hyperbolic pieces of the decomposition.
If one omits the absolute value in (1) then the volume conjecture instead involves the complex volume (MMOTY 02, Conjecture 1.2).
For on general 3-manifolds
More generally, volume conjectures state convergence of the Turaev-Viro invariants or Reshetikhin-Turaev invariants on general hyperbolic 3-manifolds to the volume or complex volume, respectively.
See (Chen-Yang 15)
For
Generalization from gauge group SU(2) to SU(n): Chen-Liu-Zhu 15
Proof strategies
As combined AdS/CFT + 3d/3d duality for wrapped M5-branes
In Gang-Kim-Lee 14b, 3.2, Gang-Kim 18 (21) it is argued that the volume conjecture for Chern-Simons theory on hyperbolic 3-manifolds is the combined statement of two dualities in string theory:
for the situation of M5-branes wrapped on (DGKV 10):
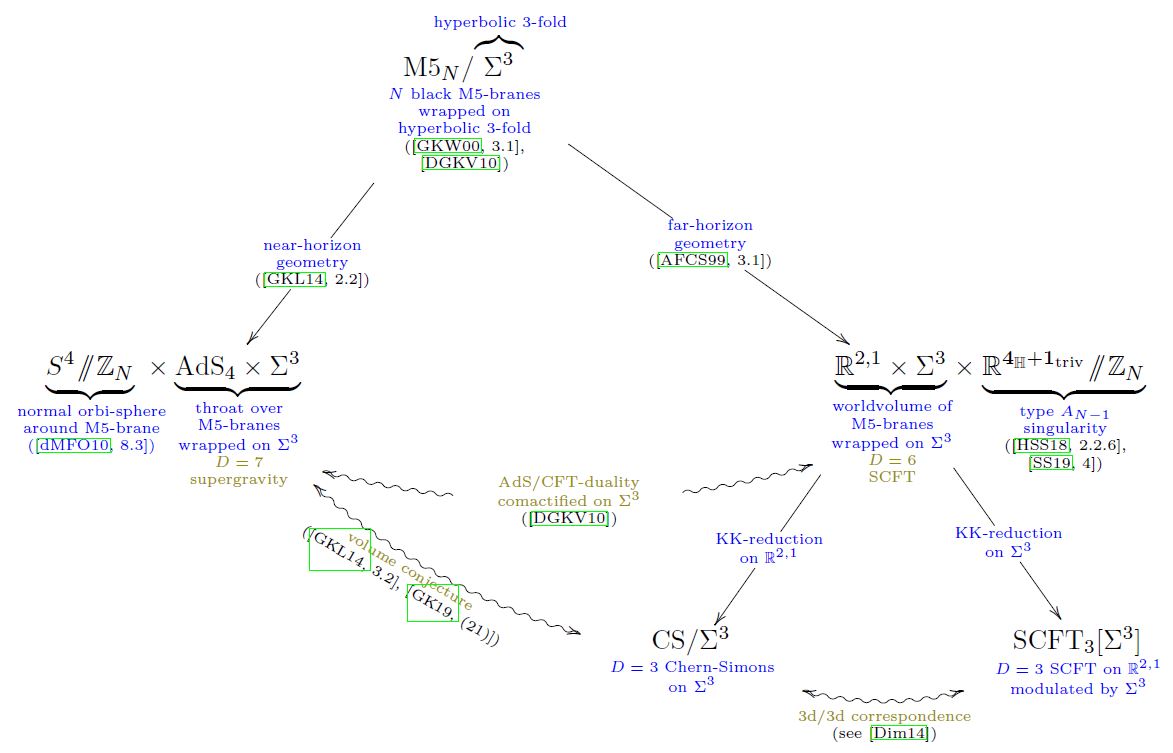
For review of the literature see also Dimofte 16, Section 4.1.
Related concepts
References
General
Original articles include
-
Rinat Kashaev, A Link Invariant from Quantum Dilogarithm, Modern Physics Letters AVol. 10, No. 19, pp. 1409-1418 (1995) (arXiv:q-alg/9504020)
-
Rinat Kashaev, The Hyperbolic Volume Of Knots From The Quantum Dilogarithm Lett. Math. Phys. 39 (1997) 269-275 (arXiv:q-alg/9601025)
-
Rinat Kashaev, O. Tirkkonen, Proof of the volume conjecture for torus knots, Journal of Mathematical Sciences (2003) 115: 2033 (arXiv:math/9912210)
-
Hitoshi Murakami, Jun Murakami, The Colored Jones Polynomial And The Simplicial Volume Of A Knot, Acta Math. 186 (2001) 85-104 (euclid.acta/1485891370)
-
Hitoshi Murakami, Jun Murakami, M. Okamoto, T. Takata, and Y. Yokota, Kashaev’s Conjecture And The Chern-Simons Invariants Of Knots And Links, Experiment. Math. 11 (2002) 427-435 (arXiv:math/0203119)
-
Hitoshi Murakami, Asymptotic Behaviors Of The Colored Jones Polynomials Of A Torus Knot, Internat. J. Math. 15 (2004) 547-555.
Generalization to Reshetikhin-Turaev construction on closed manifold, to the Turaev-Viro construction on manifolds with boundary, and to more general roots of unity than considered before is in
-
Qingtao Chen, Tian Yang, A volume conjecture for a family of Turaev-Viro type invariants of 3-manifolds with boundary (arXiv:1503.02547)
-
Dongmin Gang, Mauricio Romo, Masahito Yamazaki, All-Order Volume Conjecture for Closed 3-Manifolds from Complex Chern-Simons Theory, Commun. Math. Phys. (2018) 359: 915. (arXiv:1704.00918, doi:10.1007/s00220-018-3115-y)
Generalization to SU(n):
- Qingtao Chen, Kefeng Liu, Shengmao Zhu, Volume conjecture for -invariants (arXiv:1511.00658)
Review includes
-
Hitoshi Murakami, An Introduction to the Volume Conjecture (arXiv:1002.0126) In: Interactions Between Hyperbolic Geometry, Quantum Topology and Number Theory, Contemporary Mathematics Volume 541, AMS 2011 (doi:10.1090/conm/541)
-
Edward Witten, pp. 4 of Two Lectures On The Jones Polynomial And Khovanov Homology (arXiv:1401.6996)
-
Wikipedia, Volume conjecture
See also
-
Walter Neumann, Extended Bloch group and the Cheeger-Chern-Simons class, Geom. Topol. 8 (2004) 413-474 (arXiv:math/0307092)
-
Christian Zickert, The volume and Chern-Simons invariant of a representation, Duke Math. J., 150 (3):489-532, 2009 (arXiv:0710.2049)
-
Walter Neumann, Realizing arithmetic invariants of hyperbolic 3-manifolds, Contemporary Math 541 (Amer. Math. Soc. 2011), 233–246 (arXiv:1108.0062)
-
Stavros Garoufalidis, Dylan Thurston, Christian Zickert, The complex volume of -representations of 3-manifolds (arXiv:1111.2828, Euclid)
Via string theory
General
Speculative discussion in terms of quantum field theory or string theory includes
-
Sergei Gukov, Three-Dimensional Quantum Gravity, Chern-Simons Theory, And The A-Polynomial, Commun. Math. Phys. 255 (2005) 577-627 (arXiv:hep-th/0306165)
-
Robbert Dijkgraaf, Hiroyuki Fuji, The Volume Conjecture and Topological Strings (arXiv:0903.2084)
-
Tudor Dimofte, Sergei Gukov, Quantum Field Theory and the Volume Conjecture, Contemporary Mathematics 541 (2011), p.41-67 (arxiv:1003.4808)
-
Tudor Dimofte, Section 4.1 of: Perturbative and nonperturbative aspects of complex Chern-Simons Theory, Journal of Physics A: Mathematical and Theoretical, Volume 50, Number 44 (arXiv:1608.02961)
A conceptual explanation of the volume conjecture via analytically continued Chern-Simons theory was proposed in
- Edward Witten, Analytic Continuation Of Chern-Simons Theory, AMS/IP Stud. Adv. Math 50 (2011): 347 (arXiv:1001.2933)
(but it seems that as a sketch or strategy for a rigorous proof, it didn’t catch on).
As AdS/CFT + 3d/3d duality for wrapped M5-branes
Suggestion that the statement of the volume conjecture is really AdS-CFT duality combined with the 3d-3d correspondence for M5-branes wrapped on hyperbolic 3-manifolds:
-
Dongmin Gang, Nakwoo Kim, Sangmin Lee, Section 3.2 of: Holography of 3d-3d correspondence at Large , JHEP 04 (2015) 091 (arXiv:1409.6206)
-
Dongmin Gang, Nakwoo Kim, around (21) of: Large twisted partition functions in 3d-3d correspondence and Holography, Phys. Rev. D 99, 021901 (2019) (arXiv:1808.02797)
Last revised on November 17, 2020 at 07:41:21. See the history of this page for a list of all contributions to it.