nLab weakly globular n-fold category

Idea

Classically, models of weak $n$-categories comprise sets of cells in dimension 0 up to $n$. This is also called the globularity condition. Geometrically, it corresponds to cells having a globular shape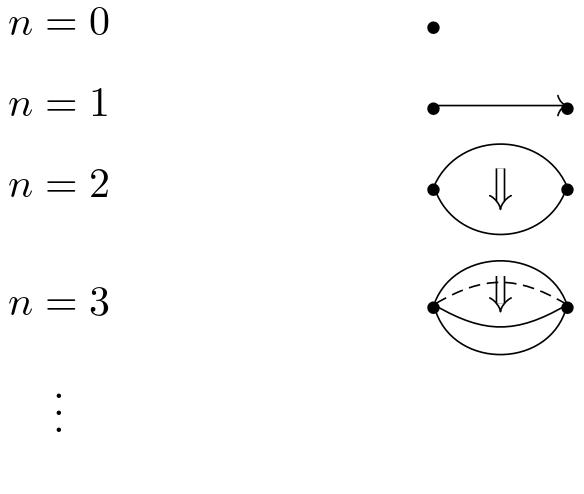

On the other hand, non-globular structures exist in higher category theory: for instance, $n$-fold categories, defined by iterated internalization

$$Cat^{0}=Set,\qquad\qquad Cat^{n}=Cat(Cat^{n-1})\;.$$

The category $n\text{-}Cat$ of strict $n$-categories is defined by iterated enrichment:

$$0\text{-}Cat=Set,\qquad\qquad n\text{-}Cat=((n-1)\text{-}Cat,\times)\text{-}Cat\;.$$

There is an embedding

$$n\text{-}Cat\hookrightarrow Cat^{n}$$

such that a strict $n$-category is an $n$-fold category in which certain substructures are discrete (that is, sets). This discreteness condition is precisely the globularity condition and the sets underlying these discrete substructures are the sets of cells in the strict $n$-category.

For instance, in the case $n=2$, strict 2-categories are double categories in which the category of objects and vertical arrows is discrete. In pictures: 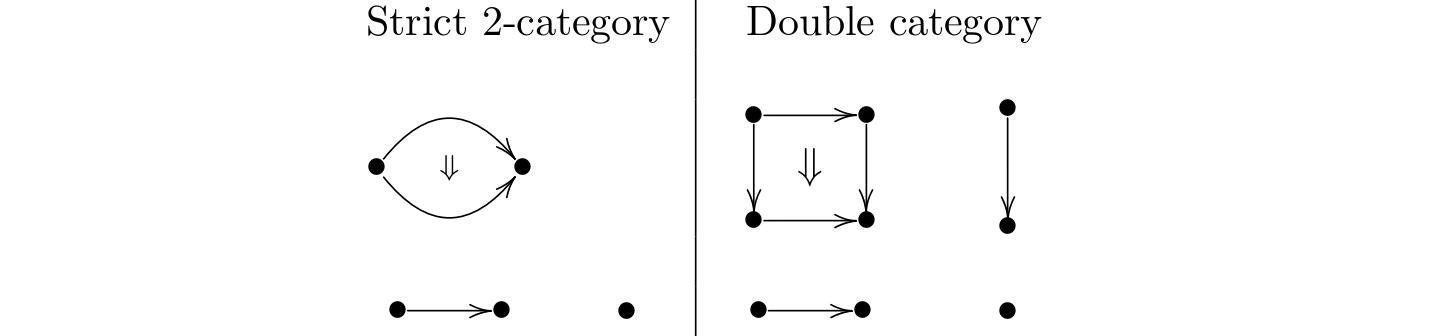We see that the picture on the right becomes the one on the left when all vertical morphisms are identities.

In the weakly globular approach to higher categories, the cells in each dimension instead of forming a set, have a higher categorical structure which is homotopically discrete, that is only equivalent (in a higher categorical sense) to a set. This condition, called weak globularity condition, is a new paradigm to weaken higher categorical structures and allows to use rigid structures, namely $n$-fold categories, to model weak $n$-categories. There are strict embeddings

$$n\text{-} Cat \hookrightarrow Cat_{wg}^{n} \hookrightarrow Cat^{n}$$

so that the category $Cat_{wg}^{n}$ of weakly globular $n$-fold categories is intermediate between strict $n$-categories and $n$-fold categories.

In the case $n=2$, a weakly globular double category $X$ is a double category satisfying two conditions: the first is the weak globularity condition, stating that the category $X_0$ of objects and vertical arrows is equivalent to a discrete category, that is it is an equivalence relation. The set $pX_0$ of connected components of $X_0$ plays the role of ‘set of objects’ in the weak structure. We therefore need to define a composition of horizontal arrows whose source and target are in the same vertical connected component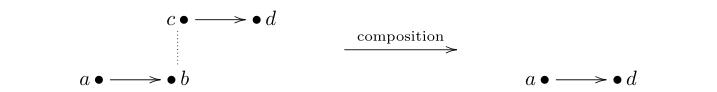

For this purpose, we impose a second condition: for each ‘staircase path’

A more concise way to express this second condition is in term of the so called induced Segal maps condition.

Weakly globular double categories have been shown by Paoli and Pronk to be suitably equivalent to bicategories.

In dimension $n\geq2$, a weakly globular $n$-fold category $X$ is an $n$-fold category which first of all needs to satisfy the weak globularity condition; namely those substructures that are discrete in the image of the embedding $n\text{-} Cat\hookrightarrow Cat^{n}$, are now instead only equivalent to sets. The precise notion we use for these substructures is the one of homotopically discrete $n$-fold categories. The latter are defined inductively, starting with equivalence relations in the case of $n=1$. When $n\geq1$, the idea of a homotopically discrete $n$-fold category is that it is an $n$-fold category suitably equivalent to a discrete one both ‘globally’ and in each simplicial dimension.

The additional conditions in the definition of $Cat_{wg}^{n}$ are given inductively in terms of induced Segal maps conditions. They guarantee the existence of weakly associative and weakly unital compositions but, like in the Tamsamani-Simpson model, their coherences are not given explicitly but they are automatically encoded in the multi-simplicial combinatorics.

Weakly globular $n$-fold categories have been shown to satisfy the homotopy hypothesis and to be suitably equivalent to the Tamsamani-Simpson model.

Homotopically discrete $n$-fold categories

The definition of weakly globular $n$-fold category requires a preliminary notion, the one of homotopically discrete $n$-fold category.

Definition

Let $Cat_{hd}^{0}=Set$. Suppose, inductively, we have defined the subcategory $Cat_{hd}^{n-1}\subset Cat^{n-1}$ of homotopically discrete $(n-1)$-fold categories. We say that the $n$-fold category $X\in Cat^{n}$ is homotopically discrete if:

a) $X$ is a levelwise equivalence relation, that is for each $(k_1,\ldots,k_{n-1})\in\Delta^{{n-1}^{op}}$, $X_{k_1,\ldots,k_{n-1}}\in Cat$ is an equivalence relation (that is, a category equivalent to a discrete one).

b) $p^{(n-1)}X\in Cat_{hd}^{n-1}$ where $(p^{(n-1)}X)_{k_1,\ldots,k_{n-1}}=p X_{k_1,\ldots,k_{n-1}}$ with $p: Cat\rightarrow Set$ the isomorphism classes of objects functor.

When $n=1$ we denote by $Cat_{hd}^{1}=Cat_{hd}^{}$ the subcategory of $Cat$ consisting of equivalence relations.

Definition

Let $X\in Cat_{hd}^{n}$. Denote by $\gamma^{(n-1)}_X:X\rightarrow p^{(n-1)}X$ the morphism given by

$$(\gamma^{(n-1)}_X)_{s_1...s_{n-1}} :X_{s_1...s_{n-1}} \rightarrow p X_{s_1...s_{n-1}}\;.$$

Denote by

$$X^d =p p^{(1)}...p^{(n-1)}X$$

and by $\gamma_{n}$ the composite

$$X\xrightarrow{\gamma^{(n-1)}}p^{(n-1)}X \xrightarrow{\gamma^{(n-2)}} p^{(n-2)}p^{(n-1)}X \rightarrow \cdots \xrightarrow{\gamma^{(0)}} X^d\;.$$

We call $\gamma_{n}$ the discretization map.

Definition

Given $X\in Cat_{hd}^{n}$, for each $a,b\in X_0^d$ denote by $X(a,b)$ the fiber at $(a,b)$ of the map

$$X_1 \xrightarrow{(d_0,d_1)} X_0\times X_0 \xrightarrow{\gamma_{n}\times\gamma_{n}} X_0^d\times X_0^d\;.$$

$X(a,b)\in Cat_{hd}^{n-1}$ should be thought of as a hom-$(n-1)$-category.

Definition

Define inductively $n$-equivalences in $Cat_{hd}^{n}$. For $n=1$, a 1-equivalence is an equivalence of categories. Suppose we have defined $(n-1)$-equivalences in $Cat_{hd}^{n-1}$. Then a map $f:X\rightarrow Y$ in $Cat_{hd}^{n}$ is an $n$-equivalence if

a) For all $a,b \in X_0^d$,

$$f(a,b):X(a,b) \rightarrow Y(f a,f b)$$

is an $(n-1)$-equivalence.

b) $p^{(n-1)}f$ is an $(n-1)$-equivalence.

The next proposition means that homotopically discrete $n$-fold categories are a higher categorical ‘fattening’ of sets.

Proposition

Let $X\in Cat_{hd}^{n}$. Then the maps $\gamma^{(n-1)}:X\rightarrow p^{(n-1)}X$ and $\gamma_{n}:X\rightarrow X^d$ are $n$-equivalences.

The three Segal-type models

There are three Segal-type models of weak $n$-categories Here $Ta^{n}$ is the Tamsamani-Simpson model and $Ta_{wg}^{n}$ (called weakly globular Tamsamani $n$-categories) is a generalization of it using weak globularity; the latter contains weakly globular $n$-fold categories as special case.

Weakly globular Tamsamani ${n}$-categories

The definition of $Ta_{wg}^{n}$ is by induction on $n$, starting with $Ta_{wg}^{1}= Cat$ and 1-equivalences being equivalences of categories. Suppose, inductively, that we defined $Ta_{wg}^{n-1}$ and $(n-1)$-equivalences. Then we define $Ta_{wg}^{n}$ through the following conditions:

a) There is an embedding of $Ta_{wg}^{n}$ into functor categories

(1)$$Ta_{wg}^{n}\hookrightarrow [\Delta^{{}^{op}},{Ta_{wg}^{n-1}}]\hookrightarrow [\Delta^{{n-1}^{op}}, Cat]$$

b) There is a truncation functor

(2)$$p^{(n-1)}:Ta_{wg}^{n}\rightarrow Ta_{wg}^{n-1}$$

$$(p^{(n-1)}X)_{k_1,\ldots, k_{n-1}}=p X_{k_1,\ldots, k_{n-1}}$$

for each $(k_1,\ldots, k_{n-1})\in\Delta^{{n-1}^{op}}$ and $X\in Ta_{wg}^{n}$, where $p: Cat\rightarrow Set$ is the isomorphism classes of objects functor.

c) $X_0$ is a homotopically discrete $(n-1)$-fold category. This comes with a $(n-1)$-equivalence $\gamma:X_0\rightarrow X_0^d$ where $X_0^d$ is a discrete $(n-1)$-fold category.

d) For each $k\geq 2$ the induced Segal maps

(3)$$\hat{\mu}_k:X_k\rightarrow {X_1\times_{X_0^d}\overset{k}{\cdots}\times_{X_0^d}X_1}$$

are $(n-1)$-equivalences in $Ta_{wg}^{n-1}$. The maps $\hat{\mu}_k$ arise from the commutativity of the diagram

e) To complete the inductive step, we define $n$-equivalences in $Ta_{wg}^{n}$. For this, given $X\in Ta_{wg}^{n}$ and $(a,b)\in X_0^d\times X_0^d$, we let $X(a,b)\subset X_1$ be the fiber at $(a,b)$ of the map

$$X_1\xrightarrow{(d_0,d_1)} X_0\times X_0 \xrightarrow{\gamma\times\gamma} X^d_0\times X^d_0\;.$$

We define a map $f:X\rightarrow Y$ in $Ta_{wg}^{n}$ to be an $n$-equivalence if the following conditions hold:

i) For all $a,b\in X_0^d$

$$f(a,b): X(a,b)\rightarrow Y(f a,f b)$$

is a $(n-1)$-equivalence.

ii) $p^{(n-1)}f$ is a $(n-1)$-equivalence.

Tamsamani ${n}$-categories

The category $Ta^{n}$ of Tamsamani $n$-categories is the full subcategory of $Ta_{wg}^{n}$ whose objects $X$ are such that $X_0$ and $X_{k_1\ldots k_r 0}$ are discrete for all $(k_1\ldots k_r)\in \Delta^{{r}^{op}}$, $1\leq r\leq n-2$.

The embedding (1) restricts to an embedding

$$Ta_{n}\hookrightarrow [\Delta^{{}^{op}},{Ta_{n-1}}]$$

and the functor $p^{(n-1)}$ in (2) restricts to

$$p^{(n-1)}:Ta^{n}\rightarrow Ta^{n-1}$$

The induced Segal maps $\hat{\mu}_k$ coincide with the Segal maps

$$X_k\rightarrow {X_1\times_{X_0}\overset{k}{\cdots}\times_{X_0}X_1}$$

and are $(n-1)$-equivalences in $Ta^{n-1}$.

Weakly globular $n$-fold categories

Let $Cat_{wg}^{1}= Cat$. Having defined the full subcategory $Cat_{wg}^{n-1}\subset Ta_{wg}^{n-1}$, the category $Cat_{wg}^{n}$ of weakly globular $n$-fold categories is the full subcategory of $Ta_{wg}^{n}$ whose objects $X$ are such that $X\in Cat^{n}$, $X_k\in Cat_{wg}^{n-1}$ for all $k\geq 0$ and $p^{(n-1)}X\in Cat_{wg}^{n-1}$.

Main results

Theorem

a) There is a functor ‘rigidification’

$$Q_n: Ta_{wg}^{n}\rightarrow Cat_{wg}^{n}$$

and for each $X\in Ta_{wg}^{n}$ an $n$-equivalence in $Ta_{wg}^{n}$ natural in $X$

$$s_n(X):Q_n X\rightarrow X.$$

b) There is a functor ‘discretization’

$$Disc_{n}:Cat_{wg}^{n}\rightarrow Ta^{n}$$

and, for each $X\in Cat_{wg}^{n}$, a zig-zag of $n$-equivalences in $Ta_{wg}^{n}$ between $X$ and $Disc_{n} X$.

The functors discretization and rigidification are used in the comparison result between Tamsamani $n$-categories and weakly globular $n$-fold categories as follows:

Theorem

The functors

$$Q_n:Ta^{n}\leftrightarrows Cat_{wg}^{n}:Disc_{n}$$

induce an equivalence of categories after localization with respect to the $n$-equivalences

$$Ta^{n}/\!\!\sim^n\;\simeq \; Cat_{wg}^{n}/\!\!\sim^n\;.$$

The groupoidal case

There is a subcategory $GCat_{wg}^{n}\subset Cat_{wg}^{n}$ of groupoidal weakly globular $n$-fold categories which is an algebraic model of homotopy $n$-types. This means that weakly globular $n$-fold categories satisfy the homotopy hypothesis. To define $GCat_{wg}^{n}$ we first consider the groupoidal version of the largest of the three Segal-type models:

Definition

The full subcategory $GTa_{wg}^{n}\subset Ta_{wg}^{n}$ of groupoidal weakly globular Tamsamani $n$-categories is defined inductively as follows.

For $n=1$, $GTa_{wg}^{1}=Gpd$ is the category of groupoids. Note that $Cat_{hd}^{}\subset GTa_{wg}^{1}$. Suppose inductively we have defined $GTa_{wg}^{n-1}\subset Ta_{wg}^{n-1}$. We define $X\in GTa_{wg}^{n}\subset Ta_{wg}^{n}$ such that

i) $X_k\in GTa_{wg}^{n-1}$ for all $k\geq 0$.

ii) $p^{(n-1)}X\in GTa_{wg}^{n-1}$.

From this definition it is immediate that homotopically discrete $n$-fold categories are a full subcategory of $GTa_{wg}^{n}$.

Definition

The category $GCat_{wg}^{n}\subset Cat_{wg}^{n}$ of groupoidal weakly globular $n$-fold categories is the full subcategory of $Cat_{wg}^{n}$ whose objects $X$ are in $GTa_{wg}^{n}$.

The category $GTa^{n}\subset Ta^{n}$ of groupoidal Tamsamani $n$-categories is the full subcategory of $Ta^{n}$ whose objects $X$ are in $GTa_{wg}^{n}$.

Proposition

The functors

$$Q_n:GTa^{n}\leftrightarrows GCat_{wg}^{n}:Disc_{n}$$

induce an equivalence of categories after localization with respect to the $n$-equivalences

$$GTa^{n}/\!\!\sim^n \;\simeq\; GCat_{wg}^{n}/\!\!\sim^n\;.$$

Since Tamsamani $n$-groupoids are a model of $n$-types, as a consequence of the previous proposition we obtain that weakly globular $n$-fold categories are an algebraic model of $n$-types.

There is an alternative more explicit way to obtain a fundamental functor

$$\mathcal{H}_{n}:n\text{-types}\rightarrow GCat_{wg}^{n}$$

based on the work of Blanc and Paoli. This work shows in particular how the notion of weak globularity arises naturally in topology.

The functor $\mathcal{H}_n$ is given by the composite

$$\mathcal{H}_n: n\text{-types}\xrightarrow{\mathcal{S}} [\Delta^{{}^{op}},Set] \xrightarrow{Or_{n}} [\Delta^{{n}^{op}},Set]\xrightarrow{\mathcal{P}_n} Gpd^{n}\;.$$

Here $\mathcal{S}$ is the singular functor and $Or_{n}$ is the functor induced by ordinal sum $or_{n}: \Delta^{{n}^{op}} \rightarrow \Delta$, that is

$$(Or_{n} X)_{p_1\ldots p_n}=X_{n-1+p_1+\ldots+ p_n}$$

The functor $\mathcal{P}_n$ is left adjoint to the $n$-fold nerve functor $N_n:Gpd^{n}\rightarrow [\Delta^{{n}^{op}},Set]$. While the computation of $\mathcal{P}_n$ is in general very difficult, this becomes easy on those multi-simplicial sets in the essential image of the functor $Or_{n}\mathcal{S}$ and one obtain

$$\mathcal{H}_n X=\hat{\pi}^{1} \hat{\pi}^{2} \cdots \hat{\pi}^{n} Or_{n} \mathcal{S} X\;.$$

where $\hat{\pi}^{(i)}$ denotes the fundamental groupoid functor in the $i^{th}$ direction. Using this expression of $\mathcal{H}_n X$ one can check that $\mathcal{H}_n X\in GCat_{wg}^{n}$. In conclusion

Theorem

The functors

$$B\circ Disc_{n}:GCat_{wg}^{n}\rightleftarrows n\text{-types}:\mathcal{H}_n$$

induce an equivalence of categories

$$GCat_{wg}^{n}/\!\!\sim^{n}\,\simeq \,\mathcal{H}\!o(n\text{-types})\;.$$

where $\mathcal{H}\!o(n\text{-types})$ is the homotopy category of $n\text{-types}$.

References

The main reference for the theory of weakly globular $n$-fold categories is the following research monograph, which contains an account of all three Segal-type models

• S. Paoli. Simplicial Methods for Higher Categories: Segal-type models of weak n-categories, volume 26 of Algebra and Applications. Springer, 2019 toc pdf.

The case $n=2$ was originally introduced in the following paper

• S. Paoli, D. Pronk, A double categorical model of weak 2-categories, Theory and Application of categories, 28, (2013), 933-980.

The theory or Tamsamani weak $n$-categories was originally developed in

• Z. Tamsamani. Sur des notions de $n$-categorie et $n$-groupoide non-strictes via des ensembles multisimpliciaux. K-theory, 16:51–99, 1999.

Tamsamani weak $n$-categories were further studied (from a model category theoretic perspective) in

• C. Simpson. Homotopy theory of higher categories, volume 19 of New Math. Monographs. Cambridge University Press, 2012.

The groupoidal case of weakly globular $n$-fold structures started in

• D. Blanc and S. Paoli. Segal-type algebraic models of $n$-types. Algebr. Geom. Topol., 14:3419–3491, 2014.

An even earlier precursor in the groupoidal case, restricted to modelling path connected $n$-types and related to the $cat_n$-groups model, can be found in

• S. Paoli. Weakly globular $cat_n$-groups and Tamsamani’s model. Adv. in Math., 222:621–727, 2009.