nLab
holographic principle of higher category theory

The general abstract principle

In higher category theory it is easy to verify that a (strict) $1$-transformation $\lambda$ between n-functors $F_1,F_2:C\to D$ between strict n-categories $C$ and $D$

$$\lambda :F_1\Rightarrow F_2$$\lambda : F_1 \Rightarrow F_2

is determined uniquely by an $(n-1)$-functor

$$\eta :C_{(n-1)}\to D^{{\Delta }^1}$$\eta : C_{(n-1)} \to D^{\Delta^1}

on the strict $(n-1)$-category obtained from $C$ by discarding the n-morphisms. (Of course, not every such $(n-1)$-functor determines such a transformation; the missing condition is “naturality” at the top level.)

Analogous statements hold for general (weak) n-categories, although they are more complicated to formulate; see below.

As with various other easy facts about category theory, these become interesting statements when realized in a concrete context where certain structures are modeled by $n$-functor categories for all $n$.

Examples in low dimension

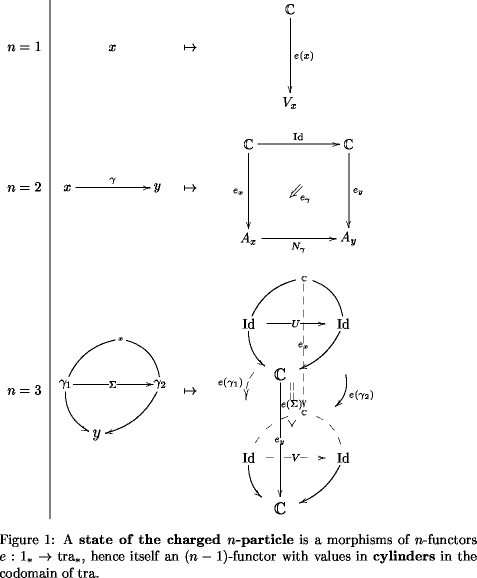
We spell out explicitly the $(n-1)$-functorial nature of transformation for low values of $n$.

• $(n=1)$ – A natural transformation $\eta$ between functors $F_1,F_2:C\to D$ between ordinary categories consists of components which are given by a function

  $$\eta :\mathrm{Obj}(C)\to \mathrm{Mor}(D)$$\eta : Obj(C) \to Mor(D)

  that sends objects of $C$ to morphisms in $D$

  $$\eta :x\mapsto (F_1(x)\stackrel{\eta (x)}{\to }{F}_2(x)).$$\eta : x \mapsto ( F_1(x) \stackrel{\eta(x)}{\to} F_2(x)) \,.

  Saying that such a function extends to a functor $C\to \mathrm{Arr}(D)$:

  $$\eta :\left(\begin{array}{c}x\\ {\downarrow }^{{\gamma }_1}\\ y\\ {\downarrow }^{{\gamma }_2}\\ z\end{array}\right)\mapsto \left(\begin{array}{ccc}{F}_1(x)& \stackrel{\eta (x)}{\to }& F_2(x)\\ {}^{F_1(f)}\downarrow & =& {\downarrow }^{F_2(f)}\\ F_1(y)& \stackrel{\eta (y)}{\to }& F_2(y)\\ {}^{F_1(g)}\downarrow & =& {\downarrow }^{F_2(g)}\\ F_1(z)& \underset{\eta (z)}{\to }& F_2(z)\end{array}\right).$$\eta : \left( \array{ x \\ \downarrow^{\mathrlap{\gamma_1}} \\ y \\ \downarrow^{\mathrlap{\gamma_2}} \\ z } \right) \;\;\; \mapsto \;\;\; \left( \array{ F_1(x) &\stackrel{\eta(x)}{\to}& F_2(x) \\ {}^{\mathllap{F_1(f)}}\downarrow &=& \downarrow^{\mathrlap{F_2(f)}} \\ F_1(y) &\stackrel{\eta(y)}{\to}& F_2(y) \\ {}^{\mathllap{F_1(g)}}\downarrow &=& \downarrow^{\mathrlap{F_2(g)}} \\ F_1(z) &\underset{\eta(z)}{\to}& F_2(z) } \right) \,.

  is equivalent to saying that these components form a natural transformation. Since there are no nontrivial 2-morphisms in $D$—in other words, the forgetful functor $\mathrm{Arr}(D)\to D\times D$ is faithful—such an extension to a functor is necessarily unique.

  So we may regard the component function of $\eta$ as a 0-functor

  $$\eta :{\mathrm{sk}}_{0}C=\mathrm{Obj}(C)\to D^{\Delta [1]}=\mathrm{Arr}(D)$$\eta : \mathbf{sk}_0 C = Obj(C) \to D^{\Delta[1]} = Arr(D)

  from the discrete category on the set of objects of $C$ to the arrow category of $D$.

• $(n=2)$ A pseudonatural transformation $\eta$ between (strict, say, for ease of of notation) 2-functors $F_1,F_2:C\to D$ between (strict, for simplicity) 2-categories is in components a 1-functor that functorially assigns pseudonaturality squares:

  $$\eta :\left(\begin{array}{c}x\\ {\downarrow }^{{\gamma }_1}\\ y\\ {\downarrow }^{{\gamma }_2}\\ z\end{array}\right)\mapsto \left(\begin{array}{ccc}{F}_1(x)& \stackrel{\eta (x)}{\to }& F_2(x)\\ {}^{F_1(f)}\downarrow & {⇙}_{\eta (f)}& {\downarrow }^{F_2(f)}\\ F_1(y)& \stackrel{\eta (y)}{\to }& F_2(y)\\ {}^{F_1(g)}\downarrow & {⇙}_{\eta (g)}& {\downarrow }^{F_2(g)}\\ F_1(z)& \underset{\eta (z)}{\to }& F_2(z)\end{array}\right)$$\eta : \left( \array{ x \\ \downarrow^{\mathrlap{\gamma_1}} \\ y \\ \downarrow^{\mathrlap{\gamma_2}} \\ z } \right) \;\;\; \mapsto \;\;\; \left( \array{ F_1(x) &\stackrel{\eta(x)}{\to}& F_2(x) \\ {}^{\mathllap{F_1(f)}}\downarrow &\swArrow_{\eta(f)}& \downarrow^{\mathrlap{F_2(f)}} \\ F_1(y) &\stackrel{\eta(y)}{\to}& F_2(y) \\ {}^{\mathllap{F_1(g)}}\downarrow &\swArrow_{\eta(g)}& \downarrow^{\mathrlap{F_2(g)}} \\ F_1(z) &\underset{\eta(z)}{\to}& F_2(z) } \right)

  We may regard this as a 1-functor

  $$\eta :{\mathrm{sk}}_{1}C\to \mathrm{Arr}(D)$$\eta : \mathbf{sk}_1 C \to Arr(D)

  from the underlying 1-category of $C$ to the arrow category of $D$, whose objects are morphisms in $D$, whose morphisms are squares in $D$, and whose composition is pasting of such squares (see double category for details).

  Again, saying that this 1-functor extends to a 2-functor from $C$ to the arrow 2-category of $D$ says precisely that these components form a pseudonatural transformation, and any such extension is unique when it exists since the forgetful 2-functor $\mathrm{Arr}(D)\to D\times D$ is locally faithful.

• $(n=3)$ – A transformation between 3-functors is in components a 2-functor that sends 2-morphisms in $C$ to cyclinders in $D$. This is shown in the $(n=3)$-row of the following diagram

  

  The pseudonaturality condition on $\eta$, which is componentwise the equation

  

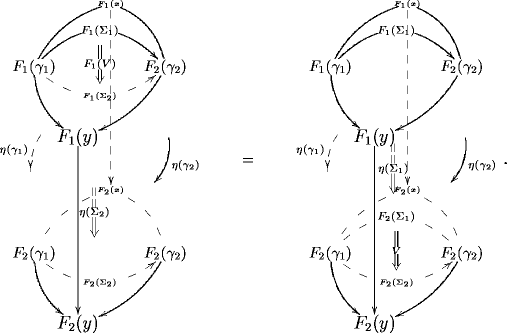
  and the fact that there are only identity 3-morphisms in $D$ implies that this already uniquely extends to a 2-functor

  $$\eta :C\to \mathrm{Arr}(D),$$\eta : C \to Arr(D) \,,

  where on the right we have the 2-category whose objects are morphisms in $D$, whose morphisms are squares in $D$ and whose 2-morphisms are cylinders bounded by these squares.

Formalizations

For strict ∞-categories modeled as globular strict ω-categories we have the following simple statement of the general principle.

Observation

For $C,D\in \mathrm{Str}n\mathrm{Cat}$ and $F_1,F_2:C\to D$ two strict $n$-functors, transformations $\eta :F_1\Rightarrow F_2$ which are in components given by $n$-functors

$$\eta :C\to D^{G_1}$$\eta : C \to D^{G_1}

are entirely specified by their underlying $(n-1)$-functors

$$\eta :C_{n-1}\to D^{G_1}.$$\eta : C_{n-1} \to D^{G_1} \,.

For weak $n$-categories analogous statements hold, but may have a less straightforward formulation. What is always true is that the transformation $\eta$ is specified by its values on $(n-1)$-morphisms (and below) and will be functorial in a weak sense on these, but these $(n-1)$-morphisms and below will usually not form an $(n-1)$-category themselves, since they will compose coherently only up to $n$-morphisms.

One way to bring the general case into the above simple form is to invoke models by semi-strict ∞-categories. By Simpson's conjecture, every ∞-category has a model in which everything is strict except possibly the identities and their unitalness coherence laws. This means that if $C$ is such a semistrict model of an $n$-category, then $C_{n-1}$ is an $(n-1)$-semicategory and the transformation

$$\eta :C_{n-1}\to D^{\Delta [1]}$$\eta : C_{n-1} \to D^{\Delta[1]}

is an $n$-functor on that. (By naturalness we have that $\eta$ is guaranteed also to respect the weak identities in $C$ in some way, but that way is not so easy to formalize.)

More generally, for any algebraic notion of weak $n$-category, there is a corresponding algebraic ”$(n-1)$-dimensional” structure containing only the operations on $(n-1)$-dimensional cells and below in the given notion of weak $n$-category. This is not in general a notion of weak $(n-1)$-category, but it may suffice to formulate the above principle precisely. If the starting notion of $n$-category had strict associativity and interchange, then the resulting $(n-1)$-dimensional structure will be a notion of $(n-1)$-semicategory.

Application in functorial QFT

For instance in FQFT one models $n$-dimensional topological quantum field theories as (∞,n)-functors on a flavor of an (∞,n)-category of cobordisms

$$Z:{\mathrm{Bord}}_n^S\to 𝒞$$Z : Bord_{n}^S \to \mathcal{C}

(where the superscript $S$ is to remind us that this may be cobordisms equipped with some extra structure).

It follows that with $Z_1,Z_2$ two such $n$-dimensional QFTs, a transformation $B:Z_1\Rightarrow Z_2$ does look in components itself like an QFT – which is twisted by $Z_1$ and $Z_2$ in some sense (see below) – , but in dimension $(n-1)$.

More specifically, if $𝒞$ is a symmetric monoidal (∞,n)-category with tensor unit $1$ there is the trivial FQFT $1$ given by the constant $(\mathrm{\infty },n)$-functor $1:{\mathrm{Bord}}_n\to 𝒞$.

One can see in examples that the transformations

$$B:Z\Rightarrow 1$$B : Z \Rightarrow \mathbf{1}

encode boundary conditions on cobordisms with boundary for the theory $Z$. Conversely, this means that one discovers on the boundary of the $n$-dimensional QFT $Z$ the $(n-1)$-dimensional QFT $B$. Or rather, this is the case if instead of natural transformations $\eta$ one uses canonical transformations: those component maps $\eta :C_{n-1}\to D^I$ that are required to be natural only with respect to the invertible $(n-1)$-morphisms in $C$.

For the case of $n=2$ and 2-dimensional cobordisms without any extra structure, a detailed version of these statements are given in (Schommer-Pries). For $n=3$ and the holographic relation between Reshetikhin–Turaev model and rational 2d CFT in FFRS-formalism some remarks are in (Schreiber).

In the study of quantum field theory and string theory such kinds of relations between $n$-dimensional QFTs and $(n-1)$-dimensional QFTs on their boundary have been called the holographic principle . The degree to which this principle has been formalized and the degree to which this formalization has been verified varies greatly. Examples include

• The boundary theory of 3-dimensional Chern-Simons theory is the 2-dimensional WZW-model.

  This is probably the oldest known holographic relation between QFTs.

• In the 2-d QFT called the Poisson sigma-model with target the Poisson Lie algebroid coming from a Poisson manifold the boundary 3-point function computes the deformation quantization of the classical system described by that Poisson manifold.

  (This was in fact used implicitly by Maxim Kontsevich to solve deformation quantization. The relation to the Poisson sigma-model was made explicit by Cattaneo and Felder.)

• The boundary theory of the 2-dimensional A-model QFT on a target space that is a complexification of a classical phase space is the 1-dimensional QFT (= quantum mechanics) that is the geometric quantization of this phase space.

  This is described at quantization via the A-model.

• The AdS/CFT correspondence conjectures specifically a holographic relation between quantum gravity on a 10-dimensional asymptotically anti-de Sitter spacetime and a superconformal Yang-Mills theory on its asymptotic boundary. More generally, this specific construction is supposed to apply, with variations, in many different dimensions.

See also higher category theory and physics.

References

The discussion of transformations between 2d FQFTs and how these encode boundary 1-branes and defect 1-bi-branes is in

• Chris Schommer-Pries, Topological defects and classifying local topological field theories in low dimension (pdf)

from slide 65 on.

A formally comparatively well understood case of QFT holography is the relation between 3-dimensional Chern-Simons theory and the 2-dimensional WZW-model. This is formalized by the Reshetikhin–Turaev model on the 3-dimensional side and the Fuchs-Runkel-Schweigert construction on the 2-dimensional side.

Remarks on how the relation between Reshitikhin-Turaev and FSR seem to have an interpretation in terms transformations between 3-functors are at

• Urs Schreiber, Towards 2-functorial CFT (blog entry)

There is it discussed how the basic string diagram that in FSR formalism encodes a field insertion on, possibly, a defect line and encodes the disk amplittudes of the CFT is the string diagram Poincaré-dual to the cylinder in a 3-category of 3-vector spaces.

For references on the holographic principle in QFT, see there.