nLab Adams–Novikov spectral sequence
Context
Homological algebra
(also nonabelian homological algebra)
Context
Basic definitions
Stable homotopy theory notions
Constructions
Lemmas
Homology theories
Theorems
Stable Homotopy theory
Ingredients
Contents
Contents
Idea
The Adams-Novikov spectral sequence is the -Adams spectral sequence, for MU.
More in detail, the Adams-Novikov spectral sequence is a class of spectral sequences, which refine the classical Adams spectral sequence by replacing ordinary cohomology with coefficients in Fp by complex cobordism cohomology theory MU. This makes the Adams-Novikov spectral sequence converge to the full homotopy groups of connective spectra, hence in particular to the full stable homotopy groups of spheres (Novikov 67, Theorems 3.1, 3.3, reviewed as Ravenel 78, Thm. 3.1).
More generally for any suitable E-infinity ring there is an Adams-Novikov-type spectral sequence involving -generalized cohomology/generalized homology. This fully general notion is often again just referred to as the -Adams spectral sequence. Accordingly, see there for more. For detailed introduction, see at Introduction to the Adams Spectral Sequence.
Properties
Adams Chart
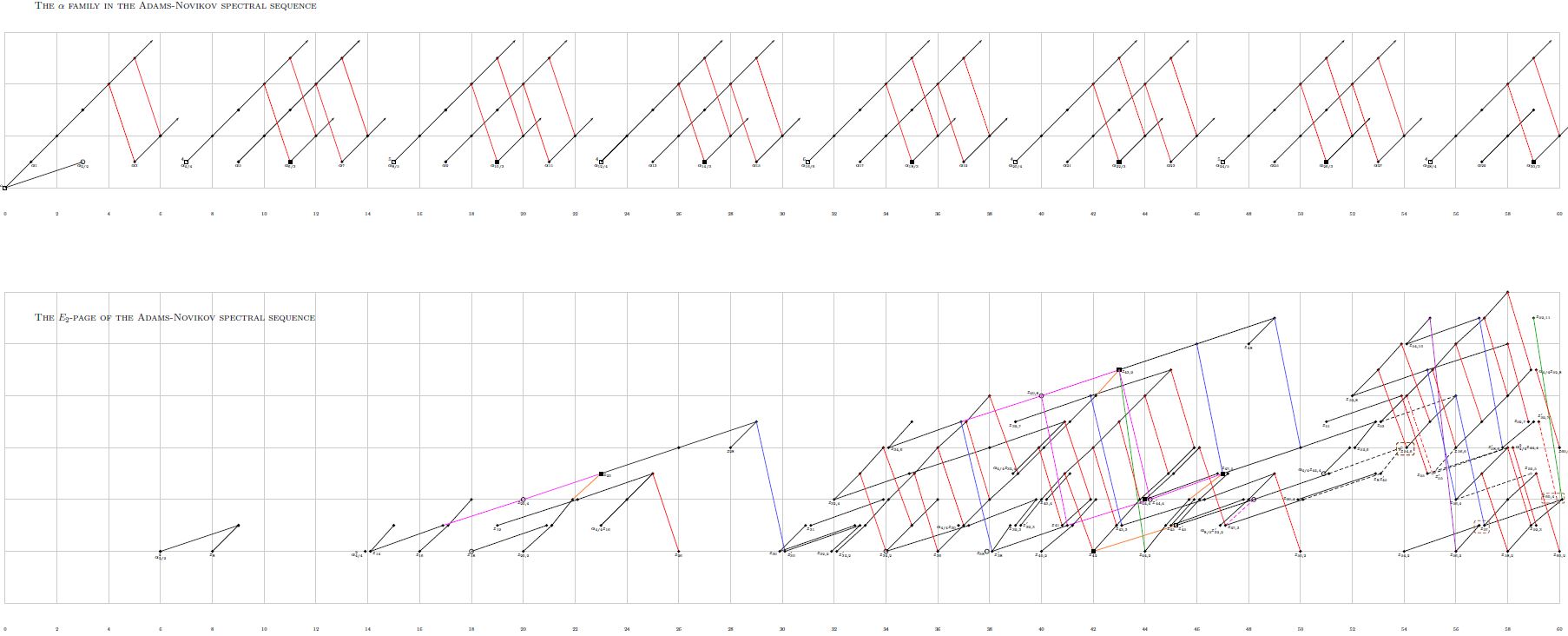
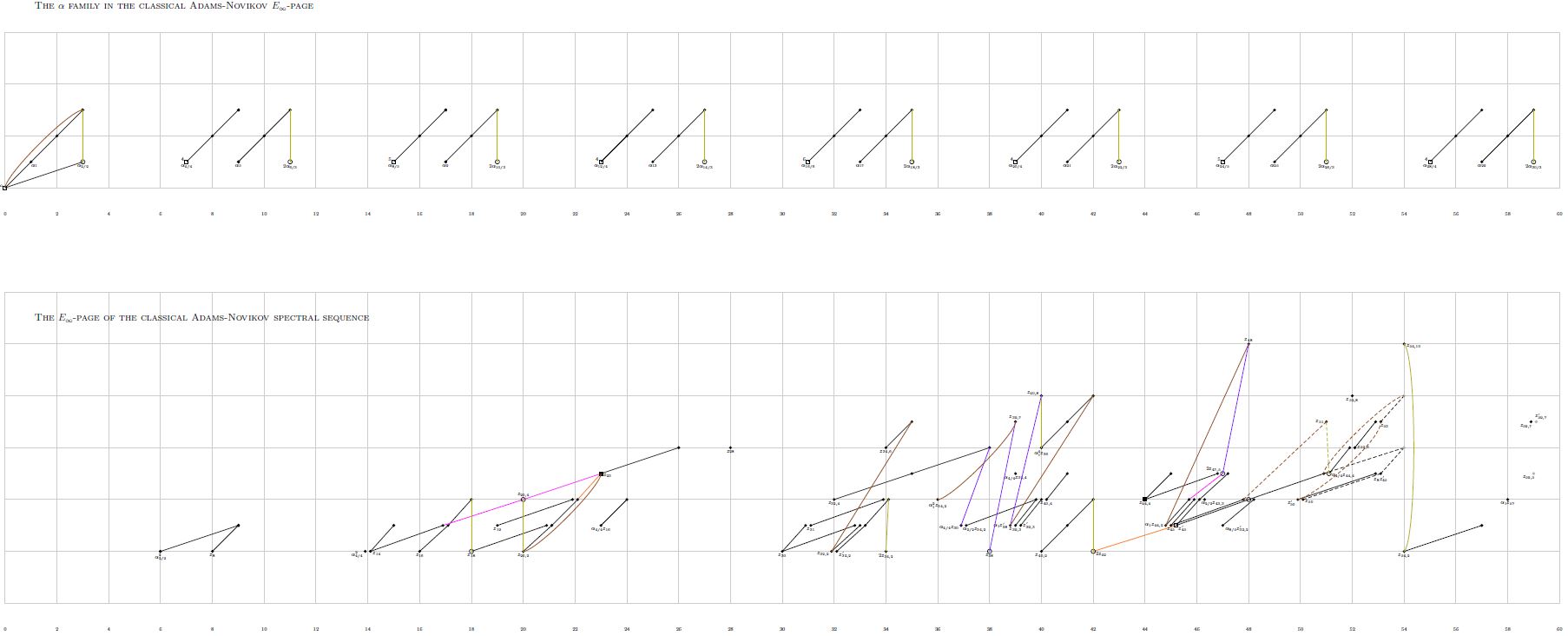
Relation to Brown-Peterson spectrum
The -component of the -term of the Adams-Novikov spectral sequence for the sphere spectrum, hence the one converging to the stable homotopy groups of spheres is
where denotes the Brown-Peterson spectrum at prime .
recalled e.g. as Ravenel, theorem 1.4.2
Related concepts
References
The generalization of the Adams spectral sequence from HA to MU is due to
- Sergei Novikov, The methods of algebraic topology from the viewpoint of cobordism theories, Izv. Akad. Nauk. SSSR. Ser. Mat. 31 (1967), 855–951 (Russian) (Novikov67)
While that article was still being translated to English, Frank Adams learned of and then lectured about this work in 1967 in Chicago. This lecture together with two later lectures in 1970 and in 1971 constitute the book
- Frank Adams, Stable homotopy and generalized homology, Chicago Lectures in mathematics, 1974
Further early development of this Adams-Novikov spectral sequence:
- Raphael Zahler, The Adams-Novikov Spectral Sequence for the Spheres, Annals of Mathematics Second Series, Vol. 96, No. 3 (Nov., 1972), pp. 480-504 (doi:10.2307/1970821)
Review:
-
Douglas Ravenel, A Novice’s guide to the Adams-Novikov spectral sequence, in: Michael Barratt, Mark Mahowald (eds.) Geometric Applications of Homotopy Theory II. Lecture Notes in Mathematics, vol 658, Springer 1978 (doi:10.1007/BFb0068728, pdf)
-
Douglas Ravenel, Complex cobordism and stable homotopy groups of spheres, page 11 of chapter I An introduction to the homotopy groups of spheres (pdf)
-
Doug Ravenel, Complex cobordism and stable homotopy groups of spheres, chapter IV -Theory and the Adams-Novikov Spectral Sequence (pdf)
-
Stanley Kochman, sections 4.7 and 5.6 of Bordism, Stable Homotopy and Adams Spectral Sequences, AMS 1996
-
Jacob Lurie, Localizations and the Adams-Novikov Spectral Sequence (pdf)
The Adams chart of the ANSS for large order has been presented in
- Daniel Isaksen, Classical and motivic Adams-Novikov charts (arXiv:1408.0248)
Last revised on February 8, 2021 at 13:53:20. See the history of this page for a list of all contributions to it.