nLab Adams spectral sequence
Context
Algebraic topology
algebraic topology – application of higher algebra and higher category theory to the study of (stable) homotopy theory
Stable Homotopy theory
Ingredients
Contents
Contents
- Idea
- Details
- The -Adams spectral sequence
- The spectral sequence
- The first page
- Flat homotopy ring spectra
- The -Steenrod algebra
- Comodules over the -Steenrod algebra
- Universal coefficient theorem
- The second page
- Convergence
- Examples
- -injective resolutions
- As derived descent in -geometry
- Related concepts
- References
Idea
The Adams spectral sequence (Adams 58) is a type of spectral sequences used for computations of stable homotopy groups of spectra in terms of their generalized homology/generalized cohomology. Given a spectrum and a ring spectrum , then under mild assumptions the Adams spectral sequence converges to the homotopy groups of the -nilpotent completion of , while under stronger assumptions the latter is the -Bousfield localization of spectra. The second page of the spectral sequence is given by the -homology of as modules over the dual -Steenrod operations. The Adams spectral sequence may be seen as a variant of the Serre spectral sequence obtained by replacing a single fibration by an “Adams resolution”.
The original classical Adams spectral sequence is the case where is ordinary homology mod , while the Adams-Novikov spectral sequence (Novikov 67) is the case where MU is complex cobordism cohomology theory or BP, Brown-Peterson theory.
Generally, for a suitable E-infinity algebra there is a corresponding -Adams(-Novikov) spectral sequence whose second page is given by -generalized cohomology and which arises as the spectral sequence of a simplicial stable homotopy type of the cosimplicial object which is the Cech nerve/Sweedler coring/Amitsur complex of . As such the Adams spectral sequence is an analog in stable homotopy theory of the Bousfield-Kan homotopy spectral sequence in unstable homotopy theory.
For a detailed introduction see at Introduction to the Adams Spectral Sequence.
Working with the Adams spectral sequence tends to be fairly involved, as is clear from the subtlety of the results it computes (notably stable homotopy groups of spheres) and as witnessed by the fact that one uses further spectral sequences just to compute the low pages of the Adams spectral sequence, e.g. the May spectral sequence and the chromatic spectral sequence.
A clear conceptual picture in higher algebra of what happens in the Adams spectral sequence (Lurie 10) has emerged via the re-formulation in (Miller 81, Hopkins 99). Survey of this perspective includes (Wilson 13).
Here one observes that for a ring spectrum, hence an E-∞ ring, the totalization of its Amitsur complex cosimplicial spectrum is really the algebraic dual incarnation of the 1-image factorization of the terminal morphism
in E-∞ geometry/spectral geometry.
Moreover, a spectrum is equivalently a quasicoherent sheaf on and is accordingly the Sweedler coring that expresses the descent property of pullled back along the cover , dually the -localization of . The Adams spectral sequence may then be seen to be the computation of the homotopy groups of the -localization of in terms of its restriction to that cover.
In general, notably for , the 1-image of is smaller than and therefore this process computes not all of , but just the restriction to that one image (for instance just the -local component). Examples of ring spectra which are “complete” with respect to the sphere spectrum in that the above 1-image coincides with notably includes the complex cobordism cohomology spectrum MU (Hopkins 99, p. 70).
That explains the relevance of the Adams-Novikov spectral sequence (noticing that the wedge summands of are the BP-spectra) and the close interplay between the ANSS and chromatic homotopy theory.
Details
The -Adams spectral sequence
We here discuss Adams spectral sequences for computation of -localization of mapping spectra for a commutative ring spectrum which is flat in a certain sense (def. below), via the “canonical” -Adams resolution introduced in (Adams 74, theorem 15.1). There are other resolutions which lead to the same spectral sequence, this we discuss below in the section on E-Injective resolutions.
The classical Adams spectral sequence is the special case of this general concept of -Adams spectral sequences given by setting the sphere spectrum and H the Eilenberg-MacLane spectrum of a prime field. This is discussed below.
The Adams-Novikov spectral sequence is the special case given by setting and MU, discussed below.
The spectral sequence
Filtered spectra
We introduce the types of spectral sequences of which the -Adams spectral sequences (def. below) are an example.
Definition
A filtered spectrum is a spectrum equipped with a sequence in the stable homotopy category (def.) of the form
Remark
More generally a filtering on an object in (stable or not) homotopy theory is a -graded sequence such that is the homotopy colimit . But for the present purpose we stick with the simpler special case of def. .
Remark
There is no condition on the morphisms in def. . In particular, they are not required to be n-monomorphisms or n-epimorphisms for any .
On the other hand, while they are also not explicitly required to have a presentation by cofibrations or fibrations, this follows automatically: by the existence of the model structure on topological sequential spectra (thm.) or equivalently (thm.) the model structure on orthogonal spectra (thm.), every filtering on a spectrum is equivalent to one in which all morphisms are represented by cofibrations or by fibrations.
This means that we may think of a filtration on a spectrum in the sense of def. as equivalently being a tower of fibrations over that spectrum.
The following definition unravels the structure encoded in a filtration on a spectrum, and motivates the concepts of exact couples and their spectral sequences from these.
Definition
(exact couple of a filtered spectrum)
Consider a spectrum and a filtered spectrum as in def. .
Write for the homotopy cofiber of its th stage, such as to obtain the diagram
where each stage
is a homotopy cofiber sequence (def.), hence equivalently (prop.) a homotopy fiber sequence, hence where
is an exact triangle (prop.).
Apply the graded hom-group functor (def.) to the above tower. This yields a diagram of -graded abelian groups of the form
where each hook at stage extends to a long exact sequence of homotopy groups (prop.) via connecting homomorphisms
If we regard the connecting homomorphism as a morphism of degree -1, then all this information fits into one diagram of the form
where each triangle is a rolled-up incarnation of a long exact sequence of homotopy groups (and in particular is not a commuting diagram!).
If we furthermore consider the bigraded abelian groups and , then this information may further be rolled-up to a single diagram of the form
Specifically, regard the terms here as bigraded in the following way
Then the bidegree of the morphisms is
| morphism | bidegree |
|---|---|
This way counts the cycles of going around the triangles:
Data of this form is called an exact couple, def. below.
Definition
An unrolled exact couple (of Adams-type) is a diagram of abelian groups of the form
such that each triangle is a rolled-up long exact sequence of abelian groups of the form
The collection of this “un-rolled” data into a single diagram of abelian groups is called the corresponding exact couple.
Definition
An exact couple is a diagram (non-commuting) of abelian groups of the form
such that this is exact in each position, hence such that the kernel of every morphism is the image of the preceding one.
The concept of exact couple so far just collects the sequences of long exact sequences given by a filtration. Next we turn to extracting information from this sequence of sequences.
Remark
The sequence of long exact sequences in def. is inter-locking, in that every appears twice:
This gives rise to the horizontal (“splicing”) composites , as shown, and by the fact that the diagonal sequences are long exact, these are differentials in that they square to zero: . Hence there is a cochain complex:
We may read off from these interlocking long exact sequences what these differentials mean, as follows. An element lifts to an element precisely if :
In order to organize this observation, notice that in terms of the exact couple of remark , the differential
is the composite
Some terminology:
Definition
observe that the composite
is a differential in that it squares to 0, due to the exactness of the exact couple:
One says that the page of the exact couple is the graded chain complex
Given a cochain complex like this, we are to pass to its cochain cohomology. Since the cochain complex here has the extra structure that it arises from an exact couple, its cohomology groups should still remember some of that extra structure. Indeed, the following says that the remaining extract structure on the cohomology of the page of an exact couple is itself again an exact couple, called the “derived exact couple”.
Proof
This is straightforward to check. For completeness we spell it out:
First consider that the morphisms are well defined in the first place.
It is clear that is well-defined.
That lands in : it lands in the image of which is in the kernel of , by exactness, hence in the kernel of by definition.
That is independent of the choice of preimage: For any , let be two preimages under , hence . This means that , hence that , hence that , hence there exists such that , hence , but in .
That vanishes on : because and hence by exactness.
That lands in : since it is defined on it lands in . By exactness this is .
That the sequence of maps is again exact:
The kernel of is those such that their preimage is still in (by exactness of the original exact couple) hence such that , hence such that .
The kernel of is the intersection of the kernel of with the kernel of , wich is still the kernel of , hence the image of , by exactness. Indeed this is also still the image of , since for every then .
The kernel of is , by exactness. Let such that , then by exactness hence , hence and so .
Definition
Given an exact couple, def. , then the induced spectral sequence of the exact couple is the sequence of pages, def. , of the induced sequence of derived exact couples, def. , lemma .
The th page of the spectral sequence is the page (def. ) of the th exact couple, denoted
Remark
So the spectral sequence of an exact couple (def. ) is a sequence of cochain complexes , where the cohomology of one is the terms of the next one:
In practice this is used as a successive stagewise approximation to the computation of a limiting term . What that limiting term is, if it exists at all, is the subject of convergence of the spectral sequence, we come to this below.
Def. makes sense without a (bi-)grading on the terms of the exact couple, but much of the power of spectral sequences comes from the cases where such a bigrading is given, since together with the sequence of pages of the spectral sequence, this tends to organize computation of the successive cohomology groups in an efficient way. Therefore consider:
Definition
Given a filtered spectrum as in def. ,
and given another spectrum , the induced spectral sequence of a filtered spectrum is the spectral sequence that is induced, by def. from the exact couple (def. ) given by def. :
with the following bidegree of the differentials:
In particular the first page is
As we pass to derived exact couples, by def. , the bidegree of and is preserved, but that of increases by with each page, since (by def. )
Similarly the first differential has degree
and so the differentials on the th page are of the form
It is conventional to depict this in tables where increases vertically and upwards and increases horizontally and to the right, so that goes up steps and always one step to the left. This is the “Adams type” grading convention for spectral sequences (different from the Serre-Atiyah-Hirzebruch spectral sequence convention (prop.)). One also says that
-
is the filtration degree;
-
is the total degree;
-
is the internal degree.
A priori all this is -graded, but we regard it as being -graded by setting
and trivially extending the definition of the differentials to these zero-groups.
-Adams filtrations
Given a homotopy commutative ring spectrum , then an -Adams spectral sequence is a spectral sequence as in def. , where each cofiber is induced from the unit morphism :
Definition
Let be two spectra (def.), and let be a homotopy commutative ring spectrum (def.) in the tensor triangulated stable homotopy category (prop.).
Then the -Adams spectral sequence for the computation of the graded abelian group
of morphisms in the stable homotopy category (def.) is the spectral sequence of a filtered spectrum (def. ) of the image under of the tower
where each hook is a homotopy fiber sequence (equivalently a homotopy cofiber sequence, prop.), hence where each
is an exact triangle (prop.), where inductively
is the derived smash product of spectra (corollary) of with the stage (cor.), and where
is the composition of the inverse derived unitor on (cor.) with the derived smash product of spectra of the unit of and the identity on .
Hence, by def , the first page is
and the differentials are of the form
A priori is -graded, but we regard it as being -graded by setting
and trivially extending the definition of the differentials to these zero-groups.
(Adams 74, theorem 15.1 page 318)
Remark
The morphism
in def. is sometimes called the Boardman homomorphism (Adams 74, p. 58).
For the sphere spectrum it reduces to a canonical morphism from stable homotopy to generalized homology (rmk.)
For HA an Eilenberg-MacLane spectrum (def.) this in turn reduces to the Hurewicz homomorphism for spectra.
This way one may think of the -Adams filtration on in def. as the result of filtering any spectrum by iteratively projecting out all its -homology. This idea was historically the original motivation for the construction of the classical Adams spectral sequence by John Frank Adams, see the first pages of (Bruner 09) for a historical approach.
It is convenient to adopt the following notation for -Adams spectral sequences (def. ):
Definition
For a homotopy commutative ring spectrum (def.), write for the homotopy fiber of its unit , i.e. such that there is a homotopy fiber sequence (equivalently a homotopy cofiber sequence, prop.) in the stable homotopy category of the form
equivalently an exact triangle (prop.) of the form
(Adams 74, theorem 15.1 page 319) Beware that for instance (Hopkins 99, proof of corollary 5.3) uses “” not for the homotopy fiber of but for its homotopy cofiber, hence for what is according to (Adams 74).
Lemma
In terms of def. , the spectra entering the definition of the -Adams spectral sequence in def. are equivalently
and
where we write
Hence the first page of the -Adams spectral sequence reads equivalently
(Adams 74, theorem 15.1 page 319)
Proof
By definition the statement holds for . Assume then by induction that it holds for some . Since the smash product of spectra-functor preserves homotopy cofiber sequences (lemma, this is part of the tensor triangulated structure of the stable homotopy category), its application to the homotopy cofiber sequence
from def. yields another homotopy cofiber sequence, now of the form
where the morphism on the right is identified as by the induction assumption, hence . Since is defined to be the homotopy fiber of , it follows that .
Remark
Terminology differs across authors. The filtration in def. in the rewriting by lemma is due to (Adams 74, theorem 15.1), where it is not give any name. In (Ravenel 84, p. 356) it is called the (canonical) Adams tower while in (Ravenel 86, def. 2.21) it is called the canonical Adams resolution. Several authors follow the latter usage, for instance (Rognes 12, def. 4.1). But (Hopkins 99) uses “Adams resolution” for the “-injective resolutions” that we discuss below and uses “Adams tower” for yet another concept, def. below. See also remark .
We proceed now to analyze the first two pages and then the convergence properties of -Adams spectral sequences of def. .
The first page
By lemma the first page of an -Adams spectral sequence (def. ) looks like
We discuss now how, under favorable conditions, these hom-groups may alternatively be computed as morphisms of -homology equipped with suitable comodule structure over a Hopf algebroid structure on the dual -Steenrod operations (The -generalized homology of (rmk.)). Then below we discuss that, as a result, the -cohomology of the first page computes the Ext-groups from the -homology of to the -homology of , regarded as -comodules.
The condition needed for this to work is the following.
Flat homotopy ring spectra
Definition
Call a homotopy commutative ring spectrum (def.) flat if the canonical right -module structure on (prop.) (equivalently the canonical left module struture, see prop. below) is a flat module.
The key consequence of the assumption that is flat in the sense of def. is the following.
Proposition
Let be a homotopy commutative ring spectrum (def.) and let be any spectrum. Then there is a homomorphism of graded abelian groups of the form
(for the canonical -modules from this prop.) given on elements
by
If is a flat module over then this is an isomorphism.
(Adams 69, lecture 3, lemma 1 (p. 68), Adams 74, part III, lemma 12.5)
Proof
First of all, that the given pairing is a well defined homomorphism (descends from to ) follows from the associativity of .
We discuss that it is an isomorphism when is flat over :
First consider the case that is a suspension of the sphere spectrum. Then (by this example, using the tensor triangulated stucture on the stable homotopy category (prop.))
and
and
Therefore in this case we have an isomorphism for all .
For general , we may without restriction assume that is represented by a sequential CW-spectrum (prop.). Then the homotopy cofibers of its cell attachment maps are suspensions of the sphere spectrum (rmk.).
First consider the case that is a CW-spectrum with finitely many cells. Consider the homotopy cofiber sequence of the st cell attachment (by that remark):
and its image under the natural morphism , which is a commuting diagram of the form
Here the bottom row is a long exact sequence since preserves homotopy cofiber sequences (by this lemma, part of the tensor triangulated structure on prop.), and since sends homotopy cofiber sequences to long exact sequences (prop.). By the same reasoning, of the homotopy cofiber sequence is long exact; and by the assumption that is flat, the functor preserves this exactness, so that also the top row is a long exact sequence.
Now by induction over the cells of , the outer four vertical morphisms are isomorphisms. Hence the 5-lemma implies that also the middle morphism is an isomorphism.
This shows the claim inductively for all finite CW-spectra. For the general statement, now use that
-
every CW-spectrum is the filtered colimit over its finite CW-subspectra;
-
the symmetric monoidal smash product of spectra (def.) preserves colimits in its arguments separately (since it has a right adjoint (prop.));
-
commutes over filtered colimits of CW-spectrum inclusions (by this lemma, since spheres are compact);
-
distributes over colimits (it being a left adjoint).
Using prop. , we find below (theorem ) that the first page of the -Adams spectral sequence may be equivalently rewritten as hom-groups of comodules over regarded as a graded commutative Hopf algebroid. We now first discuss what this means.
The -Steenrod algebra
We discuss here all the extra structure that exists on the -self homology of a flat homotopy commutative ring spectrum. For the Eilenberg-MacLane spectrum on a prime field this reduces to the classical structure in algebraic topology called the dual Steenrod algebra . Therefore one may generally speak of as being the dual -Steenrod algebra.
Without the qualifier “dual” then “-Steenrod algebra” refers to the -self-cohomology . For this Steenrod algebra (without “dual”) is traditionally considered first, and the classical Adams spectral sequence was originally formulated in terms of instead of . But one observes (Adams 74, p. 280) that the “dual” Steenrod algebra is much better behaved, at least as long as is flat in the sense of def. .
Moreover, the dual -Steenrod algebra is more fundamental in that it reflects a stacky geometry secretly underlying the -Adams spectral sequence (Hopkins 99). This is the content of the concept of “commutative Hopf algebroid” (def. below) which is equivalently the formal dual of a groupoid internal to affine schemes, def. .
A simple illustrative archetype of the following construction of commutative Hopf algebroids from homotopy commutative ring spectra is the following situation:
For a finite set consider
as the (“codiscrete”) groupoid with as objects and precisely one morphism from every object to every other. Hence the composition operation , and the source and target maps are simply projections as shown. The identity morphism (going upwards in the above diagram) is the diagonal.
Then consider the image of this structure under forming the free abelian groups , regarded as commutative rings under pointwise multiplication.
Since
this yields a diagram of homomorphisms of commutative rings of the form
satisfying some obvious conditions. Observe that here
-
the two morphisms are and , respectively, where denotes the unit element in ;
-
the morphism is the multiplication in the ring ;
-
the morphism
is given by .
All of the following rich structure is directly modeled on this simplistic example. We simply
-
replace the commutative ring with any flat homotopy commutative ring spectrum ,
-
replace tensor product of abelian groups with derived smash product of spectra;
-
and form the stable homotopy groups of all resulting expressions.
Definition
Let be a homotopy commutative ring spectrum (def.) which is flat according to def. .
Then the dual -Steenrod algebra is the pair of graded abelian groups
(rmk.) equipped with the following structure:
-
the graded commutative ring structure
induced from being a homotopy commutative ring spectrum (prop.);
-
the graded commutative ring structure
induced from the fact that with also is canonically a homotopy commutative ring spectrum (exmpl.), so that also is a graded commutative ring (prop.);
-
the homomorphism of graded commutative rings
induced under from
-
the homomorphisms of graded commutative rings
and
induced under from the homomorphisms of commutative ring spectra
and
respectively (exmpl.);
-
the homomorphism of graded commutative rings
induced under from
regarded as a homomorphism of homotopy commutative ring spectra (exmpl.);
-
the homomorphisms graded commutative rings
induced under from the braiding
regarded as a homomorphism of homotopy commutative ring spectra (exmpl.).
(Adams 69, lecture 3, pages 66-68)
Notice that (as verified by direct unwinding of the definitions):
Lemma
For a homotopy commutative ring spectrum (def.), consider with its canonical left and right -module structure as in this prop.. These module structures coincide with those induced by the ring homomorphisms and from def. .
These two actions need not strictly coincide, but they are isomorphic:
Proposition
For a homotopy commutative ring spectrum (def.), consider with its canonical left and right -module structure (prop.). Since is a commutative monoid, this right module structure may equivalently be regarded as a left-module, too. Then the braiding
constitutes a module isomorphism (def.) between these two left module structures.
Proof
On representatives as in the proof of (this propo.), the original left action is given by (we are notationally suppressing associators throughout)
while the other left action, induced from the canonical right action, is given by
So in order that represents a module homomorphism under , it is sufficient that the following diagram commutes (we write for to make the action of the braiding more manifest)
But since is a commutative monoid (def.), it satisfies so that we may factor this diagram as follows:
Here the top square commutes by coherence of the braiding (rmk) since both composite morphisms correspond to the same permutation, while the bottom square commutesm due to the naturality of the braiding. Hence the total rectangle commutes.
The dual -Steenrod algebras of def. evidently carry a lot of structure. The concept organizing this is that of_commutative Hopf algebroids.
Definition
A graded commutative Hopf algebroid is an internal groupoid in the opposite category of -graded commutative rings, regarded with its cartesian monoidal category structure.
(e.g. Ravenel 86, def. A1.1.1)
Remark
We unwind def. . For , write for the same object, but regarded as an object in .
An internal category in is a diagram in of the form
(where the fiber product at the top is over on the left and on the right) such that the pairing defines an associative composition over , unital with respect to . This is an internal groupoid if it is furthemore equipped with a morphism
acting as assigning inverses with respect to .
The key basic fact to use in order to express this equivalently in terms of algebra is that tensor product of commutative rings exhibits the cartesian monoidal category structure on , see at CRing – Properties – Cocartesian comonoidal structure:
This means that the above is equivalently a diagram in of the form
as well as
and satisfying formally dual conditions, spelled out as def. below. Here
-
are called the left and right unit maps;
-
is called the co-unit;
-
is called the comultiplication;
-
is called the antipode or conjugation
Remark
Generally, in a commutative Hopf algebroid, def. , the two morphisms from remark need not coincide, they make genuinely into a bimodule over , and it is the tensor product of bimodules that appears in remark . But it may happen that they coincide:
An internal groupoid for which the domain and codomain morphisms coincide, , is euqivalently a group object in the slice category over .
Dually, a commutative Hopf algebroid for which and happen to coincide is equivalently a commutative Hopf algebra over .
Writing out the formally dual axioms of an internal groupoid as in remark yields the following equivalent but maybe more explicit definition of commutative Hopf algebroids, def.
Definition
A commutative Hopf algebroid is
-
two commutative rings, and ;
-
ring homomorphisms
-
(left/right unit)
;
-
(comultiplication)
;
-
(counit)
;
-
(conjugation)
-
such that
-
(co-unitality)
-
(identity morphisms respect source and target)
;
-
(identity morphisms are units for composition)
;
-
(composition respects source and target)
-
;
-
-
-
(co-associativity) ;
-
(inverses)
-
(inverting twice is the identity)
;
-
(inversion swaps source and target)
; ;
-
(inverse morphisms are indeed left and right inverses for composition)
the morphisms and induced via the coequalizer property of the tensor product from and , respectively
and
satisfy
and
.
-
(Adams 69, lecture 3, pages 62-66, Ravenel 86, def. A1.1.1)
Remark
In (Adams 69, lecture 3, page 60) the terminology used is “Hopf algebra in a fully satisfactory sense” with emphasis that the left and right module structure may differ. According to (Ravenel 86, first page of appendix A1) the terminology “Hopf algebroid” for this situation is due to Haynes Miller.
Example
For a commutative ring, then becomes a commutative Hopf algebroid over , formally dual (via def. ) to the pair groupoid on .
For a finite set and , then this reduces to the motivating example from above.
It is now straightforward, if somewhat tedious, to check that:
Proposition
Let be a homotopy commutative ring spectrum (def.) which is flat according to def. , then the dual -Steenrod algebra with the structure maps from prop. is a graded commutative Hopf algebroid according to def. :
(Adams 69, lecture 3, pages 67-71, Ravenel 86, chapter II, prop. 2.2.8)
Proof
One observes that satisfies the axioms of a commutative Hopf algebroid object in homotopy commutative ring spectra, over , by direct analogy to example (one just has to verify that the symmetric braidings go along coherently, which works by use of the coherence theorem for symmetric monoidal categories (rmk.)). Applying the functor that forms stable homotopy groups to all structure morphisms of yields the claimed structure morphisms of .
We close this subsection on commutative Hopf algebroids by discussion of their isomorphism classes, when regarded dually as affine groupoids:
Definition
Given an internal groupoid in (def. , remark )
then its affife scheme of isomorphism classes of objects is the coequlizer? of the source and target morphisms
Hence this is the formal dual of the equalizer of the left and right unit (def. )
By example every commutative ring gives rise to a commutative Hopf algebroid over . The core of is the formal dual of the corresponding affine scheme of isomorphism classes according to def. :
Definition
For a commutative ring, its core is the equalizer in
A ring which is isomorphic to its core is called a solid ring.
(Bousfield-Kan 72, §1, def. 2.1, Bousfield 79, 6.4)
Proposition
The core of any ring is solid (def. ):
Proposition
The following is the complete list of solid rings (def. ) up to isomorphism:
-
The localization of the ring of integers at a set of prime numbers (def. )
-
for ;
-
the product rings
for such that each prime factor of is contained in the set of primes ;
-
the ring cores of product rings
where are infinite sets of primes and are positive natural numbers.
(Bousfield-Kan 72, prop. 3.5, Bousfield 79, p. 276)
Comodules over the -Steenrod algebra
Definition
Let be a homotopy commutative ring spectrum (def.) which is flat according to def. .
For any spectrum, say that the comodule structure on (rmk.)) over the dual -Steenrod algebra (def. ) is
-
the canonical structure of a -module (according to this prop.);
-
the homomorphism of -modules
Definition
Given a graded commutative Hopf algebroid over as in def. , hence an internal groupoid in , then a comodule ring over it is an action in of that internal groupoid.
In the same spirit, a comodule over a commutative Hopf algebroid (not necessarily a comodule ring) is a quasicoherent sheaf on the corresponding internal groupoid (regarded as a (algebraic) stack) (e.g. Hopkins 99, prop. 11.6). Explicitly in components:
Definition
Given a -graded commutative Hopf algebroid over (def. ) then a left comodule over is
-
(co-action) a homomorphism of graded -modules
;
such that
-
(co-unitality)
;
-
(co-action property)
.
A homomorphism between graded comodules is a homomorphism of underlying graded -modules such that the following diagram commutes
We write
for the resulting category of left comodules over . Analogously for right comodules. The notation for the hom-sets in this category is abbreviated to
A priori this is an Ab-enriched category, but it is naturally further enriched in graded abelian groups:
we may drop in the above definition of comodule homomorphisms the condition that the underlying morphism be grading-preserving. Say that has degree if it increases degree by . This gives a -graded hom-group
Example
For a commutative Hopf algebroid, then becomes a left -comodule (def. ) with coaction given by the right unit
Proof
The required co-unitality property is the dual condition in def.
of the fact in def. that identity morphisms respect sources:
The required co-action property is the dual condition
of the fact in def. that composition of morphisms in a groupoid respects sources
Proposition
Let be a homotopy commutative ring spectrum (def.) which is flat according to def. , and for any spectrum, then the morphism from def. makes into a comodule (def. ) over the dual -Steenrod algebra (def. )
(Adams 69, lecture 3, pages 67-71, Ravenel 86, chapter II, prop. 2.2.8)
Example
Given a commutative Hopf algebroid over , def. , then itself becomes a left -comodule (def. ) with coaction given by
and a right -comodule with coaction given by
More generally:
Proposition
Given a commutative Hopf algebroid over , there is a free-forgetful adjunction
between the category of -comodules, def. and the category of modules over , where the cofree functor is right adjoint.
Moreover:
-
The co-free -comodule on an -module is equipped with the coaction induced by the comultiplication in .
-
The adjunct of a comodule homomorphism
is its composite with the counit of
The proof is formally dual to the proof that shows that constructing free modules is left adjoint to the forgetful functor from a category of modules to the underlying monoidal category (prop.). But since the details of the adjunction isomorphism are important for the following discussion, we spell it out:
Proof
A homomorphism into a co-free -comodule is a morphism of -modules of the form
making the following diagram commute
Consider the composite
i.e. the “corestriction” of along the counit of . By definition this makes the following square commute
Pasting this square onto the bottom of the previous one yields
Now due to co-unitality, the right right vertical composite is the identity on . But this means by the commutativity of the outer rectangle that is uniquely fixed in terms of by the relation
This establishes a natural bijection
and hence the adjunction in question.
Proposition
Consider a commutative Hopf algebroid over , def. . Any left comodule over (def. ) becomes a right comodule via the coaction
where the isomorphism in the middle the is braiding in and where is the conjugation map of .
Dually, a right comodule becoomes a left comodule with the coaction
Definition
Given a commutative Hopf algebroid over , def. , and given a right -comodule and a left comodule (def. ), then their cotensor product is the kernel of the difference of the two coaction morphisms:
If both and are left comodules, then their cotensor product is the cotensor product of with regarded as a right comodule via prop. .
e.g. (Ravenel 86, def. A1.1.4).
Example
Given a commutative Hopf algebroid over , (def.), and given a left -comodule (def.). Regard itself canonically as a right -comodule via example . Then the cotensor product
is called the primitive elements of :
Proposition
Given a commutative Hopf algebroid over , def. , and given two left -comodules (def. ), then their cotensor product (def. ) is commutative, in that there is an isomorphism
(e.g. Ravenel 86, prop. A1.1.5)
Lemma
Given a commutative Hopf algebroid over , def. , and given two left -comodules (def. ), such that is projective as an -module, then
-
The morphism
gives the structure of a right -comodule;
-
The cotensor product (def. ) with respect to this right comodule structure is isomorphic to the hom of -comodules:
Hence in particular
(e.g. Ravenel 86, lemma A1.1.6)
Remark
In computing the second page of -Adams spectral sequences, the second statement in lemma is the key translation that makes the comodule Ext-groups on the page be equivalent to a Cotor-groups. The latter lend themselves to computation, for instance via Lambda-algebra or via the May spectral sequence.
Universal coefficient theorem
The key use of the Hopf coalgebroid structure of prop. for the present purpose is that it is extra structure inherited by morphisms in -homology from morphisms of spectra. Namely forming -homology of a morphism of a spectra does not just produce a morphism of -homology groups
but in fact produces homomorphisms of comodules over
This is the statement of lemma below. The point is that -comodule homomorphism are much more rigid than general abelian group homomorphisms and hence closer to reflecting the underlying morphism of spectra .
In good cases such an approximation of homotopy by homology is in fact accurate, in that is an isomorphism. In such a case (Adams 74, part III, section 13) speaks of a “universal coefficient theorem” (the coefficients here being .)
One such case is exhibited by prop. below. This allows to equivalently re-write the first page of the -Adams spectral sequence in terms of -homology homomorphisms in theorem below.
Lemma
For any two spectra, the morphism (of -graded abelian) generalized homology groups given by smash product with (rmk.)
factors through the forgetful functor from -comodule homomorphisms (def. ) over the dual -Steenrod algebra (def. ):
where and are regarded as -Steenrod comodules according to def. , prop. .
Proof
By def. we need to show that for a morphism in then the following diagram commutes
By def. and prop. this is the image under foming stable homotopy groups of the following diagram in :
But that this diagram commutes is simply the functoriality of the derived smash product of spectra as a functor on the product category .
Proposition
Let be a homotopy commutative ring spectrum (def.), and let be two spectra such that is a projective module over (via this prop.).
Then the homomorphism of graded abelian groups
given by
is an isomorphism.
(Schwede 12, chapter II, prop. 6.20)
Proof
First of all we claim that the morphism in question factors as
where
-
denotes the category of homotopy module spectra over (def.)
-
the first morphisms is the free-forgetful adjunction isomorphism for forming free (prop.) -homotopy module spectra
-
the second morphism is the respective component of the composite of the forgetful functor from -homotopy module spectra back to with the functor that forms stable homotopy groups.
This is because (by this prop.) the first map is given by first smashing with and then postcomposing with the -action on the free module , which is the pairing (prop.).
Hence it is sufficient to show that the morphism on the right is an isomorphism.
We show more generally that for any two -homotopy module spectra (def.) such that is a projective module over , then
is an isomorphism.
To see this, first consider the case that is in fact a -free module.
This implies that there is a basis and a homomorphism
of -homotopy module spectra, such that this is a stable weak homotopy equivalence.
Observe that this sits in a commuting diagram of the form
where
-
the left vertical isomorphism exhibits wedge sum of spectra as the coproduct in the stable homotopy category (lemma);
-
the bottom isomorphism is from this prop.;
-
the right vertical isomorphism is that of the free-forgetful adjunction for modules over .
Hence the top horizontal morphism is an isomorphism, which was to be shown.
Now consider the general case that is a projective module over . Since (graded) projective modules are precisely the retracts of (graded) free modules (prop.), there exists a diagram of -modules of the form
which induces the corresponding split idempotent of -modules
As before, by freeness this is actually the image under of an idempotent of homotopy ring spectra
and so in particular of spectra.
Now in the stable homotopy category all idempotents split (prop.), hence there exists a diagram of spectra of the form
with .
Consider the composite
Since it follows that under this is an isomorphism, then that in the stable homotopy category.
In conclusion this exhibits as a retract of an free -homotopy module spectrum
hence of a spectrum for which the morphism in question is an isomorphism. Since the morphism in question is natural, its value on is a retract in the arrow category of an isomorphism, hence itself an isomorphism (lemma).
Remark
A stronger version of the statement of prop. , with the free homotopy -module spectrum replaced by any homotopy -module spectrum , is considered in (Adams 74, chapter III, prop. 13.5) (“universal coefficient theorem”). Strong conditions are considered that ensure that
is an isomormphism (expressing the -cohomology of as the -linear dual of the -homology of ).
For the following we need only the weaker but much more general statement of prop. , and in fact this is all that (Adams 74, p. 323) ends up using, too.
With this we finally get the following statement, which serves to identify maps of certain spectra with their induced maps on -homology:
Proposition
Let be a homotopy commutative ring spectrum (def.), and let be two spectra such that
-
is a projective module over (via this prop.).
is an isomorphism (where the isomophism on the right is that of prop. ).
(Adams 74, part III, page 323)
Proof
Observe that the following diagram commutes:
where
To see that this indeed commutes, notice that
-
the top morphism sends to by definition;
-
the right vertical morphism sends this further to , by the proof of prop. (which says that the map is given by postcomposition with the counit of ) and def. (which says that this counit is represented by );
-
by prop. this is the same as the action of the left diagonal morphism.
But now
and so it follows that the top horizontal morphism is an isomorphism, too.
In conclusion:
Theorem
Let be a homotopy commutative ring spectrum (def.), and let be two spectra such that
-
is a projective module over (via this prop.).
Then the first page of the -Adams spectral sequence, def. , for is isomorphic to the following chain complex of graded homs of comodules (def. ) over the dual -Steenrod algebra (prop. ):
(Adams 74, theorem 15.1 page 323)
The second page
Theorem
Let be a homotopy commutative ring spectrum (def.), and let be two spectra such that
-
is a projective module over (via this prop.).
Then the entries of the second page of the -Adams spectral sequence for (def. ) are the Ext-groups of commutative Hopf algebroid-comodules (def. ) over the commutative Hopf algebroid structure on the dual -Steenrod algebra from prop. :
(On the right is the degree that goes with any Ext-functor, and the “internal degree” is the additional degree of morphisms between graded modules from def. .)
In the special case that is the sphere spectrum, then (by prop. ) these are equivalently Cotor-groups
(Adams 74, theorem 15.1, page 323)
Proof
By theorem , under the given assumptions the first page reads
By remark the second page is the cochain cohomology of this complex. Hence by the standard theory of derived functors in homological algebra (see the section Via acyclic resolutions), it is now sufficient to see that:
-
the category (def. , prop. ) is an abelian category with enough injectives (so that all right derived functors on exist);
-
the first page graded chain complex is the image under the hom-functor of an -acyclic resolution of (so that its cohomology indeed computes the Ext-derived functor (theorem)).
That is an abelian category is lemma below, and that it has enough injectives is lemma .
Lemma below shows that is a resolution of in . By prop. it is a resolution by cofree comodules (def. ). That these are -acyclic is lemma below.
-Adams resolutions
We discuss that the first page of the -Adams spectral sequence indeed exhibits a resolution as required by the proof of theorem .
Lemma
Given an -Adams spectral sequence as in def. , then the sequences of morphisms
are short exact, hence their splicing of short exact sequences
is a long exact sequence, exhibiting the graded chain complex as a resolution of .
(Adams 74, theorem 15.1, page 322)
Proof
Consider the image of the defining homotopy cofiber sequence
under the functor . This is itself a homotopy cofiber sequence of the form
(due to the tensor triangulated structure of the stable homotopy category, prop.).
Applying the stable homotopy groups functor (lemma) to this yields a long exact sequence (prop.)
But in fact this splits: by unitality of , the product operation on the homotopy commutative ring spectrum is a left inverse to in that
Therefore is a monomorphism, hence its kernel is trivial, and so by exactness . This means that the above long exact sequence collapses to short exact sequences.
Homological co-algebra
We discuss basic aspects of homological algebra in categories of comodules (def. ) over commutative Hopf algebroids (def. ), needed in the proof of theorem .
Lemma
Let be a commutative Hopf algebroid over (def. , ), such that the right -module structure on induced by is a flat module.
Then the category of comodules over (def. ) is an abelian category.
(e.g. Ravenel 86, theorem A1.1.3)
Proof
It is clear that, without any condition on the Hopf algebroid, is an additive category.
Next we need to show if is flat over , that then this is also a pre-abelian category, in that kernels and cokernels exist.
To that end, let be a morphism of comodules, hence a commuting diagram in Mod of the form
Consider the kernel of in Mod and its image under
By the assumption that is a flat module over , also is a kernel. Hence by the universal property of kernels and the commutativity of the square o the right, there exists a unique vertical morphism as shown on the left, making the left square commute. This means that the -module uniquely inherits the structure of a -comodule such as to make a comodule homomorphism. By the same universal property it follows that with this comodule structure is in fact the kernel of in .
The argument for the existence of cokernels proceeds formally dually. Hence is a pre-abelian category.
But it also follows from this construction that the comparison morphism
formed in has underlying it the corresponding comparison morphism in . There this is an isomorphism by the fact that the category of modules is an abelian category, hence it is an isomorphism also in . So the latter is in fact an abelian category itself.
Lemma
Let be a commutative Hopf algebroid over (def. , ), such that the right -module structure on induced by is a flat module.
Then
-
every co-free -comodule (def. ) on an injective module over is an injective object in ;
-
has enough injectives (def.) if the axiom of choice holds in the ambient set theory.
(e.g. Ravenel 86, lemma A1.2.2)
Proof
First of all, assuming the axiom of choice, then the category of modules has enough injectives (by this proposition).
Now by prop. we have the adjunction
Observe that the left adjoint is a faithful functor (being a forgetful functor) and that, by the proof of lemma , it is an exact functor. This implies that
-
for an injective module, then the co-free comodule is an injective object in (by this lemma);
-
for any object, and for a monomorphism of -modules into an injective -module, then the adjunct is a monomorphism (by this lemma)) hence a monomorpism into an injective comodule, by the previous item.
Hence has enough injective objects (def.).
Lemma
Let be a commutative Hopf algebroid over (def. , ), such that the right -module structure on induced by is a flat module. Let be a -comodule (def. ) such that the underlying -module is a projective module (a projective object in Mod).
Then (assuming the axiom of choice in the ambient set theory) every co-free comodule (prop. ) is an -acyclic object for the hom functor .
Proof
We need to show that the derived functors vanish in positive degree on all co-free comodules, hence on , for all .
To that end, let be an injective resolution of in . By lemma then is a sequence of injective objects in and by the assumption that is flat over it is an injective resolution of in . Therefore the derived functor in question is given by
Here the second equivalence is the cofree/forgetful adjunction isomorphism of prop. , while the last equality then follows from the assumption that the -module underlying is a projective module (since hom functors out of projective objects are exact functors (here) and since derived functors of exact functors vanish in positive degree (here)).
With lemma the proof of theorem is completed.
Convergence
We discuss the convergence of -Adams spectral sequences (def. ), i.e. the identification of the “limit”, in an appropriate sense, of the terms on the th page of the spectral sequence as goes to infinity.
If an -Adams spectral sequence converges, then it converges not necessarily to the full stable homotopy groups , but to some localization of them. This typically means, roughly, that only certain -torsion subgroups in for some prime numbers are retained. We give a precise discussion below in Localization and adic completion of abelian groups.
If one knows that is a finitely generated abelian group (as is the case notably for by the Serre finiteness theorem) then this allows to recover the full information from its pieces: by the fundamental theorem of finitely generated abelian groups (prop. below) these groups are direct sums of powers of the infinite cyclic group with finite cyclic groups of the form , and so all one needs to compute is the powers “one prime at a time”. This we review below in Primary decomposition of abelian groups.
The deeper reason that -Adams spectral sequences tend to converge to localizations of the abelian groups of morphisms of spectra, is that they really converge to (the actual homotopy groups of) localizations of spectra. This is more than just a reformulation, because the localization at the level of spectra determies the filtration which controls the nature of the convergence. We discuss this localization of spectra below in Localization and nilpotent completion of spectra.
Then we state convergence properties of -Adams spectral sequences below in Convergence statements.
Primary decomposition of abelian groups
An -Adams spectral sequence typically converges (discussed below) not to the full stable homotopy groups , but just to some piece which on the finite direct summands consists only of p-primary groups for some prime numbers that depend on the nature of the homotopy ring spectrum . Here we review basic facts about -primary decomposition of finite abelian groups and introduce their graphical calculus (remark below) which will allow to read off these -primary pieces from the stable page of the -Adams spectral sequnce.
Theorem
(fundamental theorem of finitely generated abelian groups)
Every finitely generated abelian group is isomorphic to a direct sum of p-primary cyclic groups (for a prime number and a natural number ) and copies of the infinite cyclic group :
The summands of the form are also called the p-primary components of . Notice that the need not all be distinct.
fundamental theorem of finite abelian groups:
In particular every finite abelian group is of this form for , hence is a direct sum of cyclic groups.
fundamental theorem of cyclic groups:
In particular every cyclic group is a direct sum of cyclic groups of the form
where all the are distinct and is the maximal power of the prime factor in the prime decomposition of .
Specifically, for each natural number dividing it contains as the subgroup generated by . In fact the lattice of subgroups of is the formal dual of the lattice of natural numbers ordered by inclusion.
(e.g. Roman 12, theorem 13.4, Navarro 03) for cyclic groups e.g. (Aluffi 09, pages 83-84)
This is a special case of the structure theorem for finitely generated modules over a principal ideal domain.
Example
For and two distinct prime numbers, , then there is, up to isomorphism, precisely one abelian group of order , namely
This is equivalently the cyclic group
The isomorphism is given by sending to .
Example
Moving up, for two distinct prime numbers and , there are exactly two abelian groups of order , namely and . The latter is the cyclic group of order . For instance, .
Example
Similarly, there are four abelian groups of order , three abelian groups of order , and so on.
More generally, theorem may be used to compute exactly how many abelian groups there are of any finite order (up to isomorphism): write down its prime factorization, and then for each prime power appearing therein, consider how many ways it can be written as a product of positive powers of . That is, each partition of yields an abelian group of order . Since the choices can be made independently for each , the numbers of such partitions for each are then multiplied.
Of all these abelian groups of order , of course, one of them is the cyclic group of order . The fundamental theorem of cyclic groups says it is the one that involves the one-element partitions , i.e. the cyclic groups of order for each .
Remark
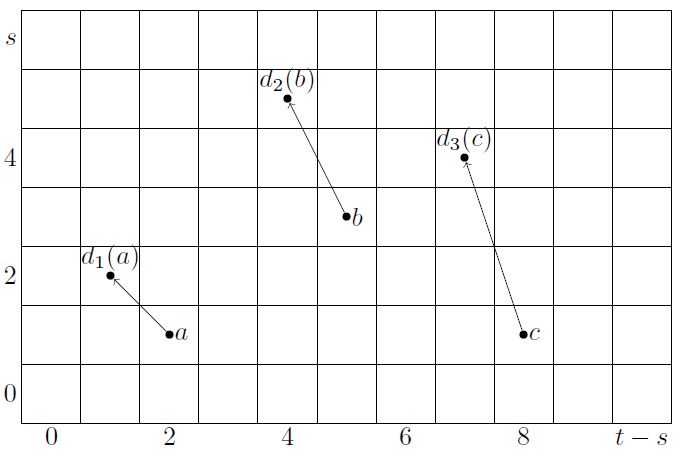
(graphical representation of -primary decomposition)
Theorem says that for any prime number , the p-primary part of any finitely generated abelian group is determined uniquely up to isomorphism by
-
a total number of powers of ;
-
a partition .
The corresponding p-primary group is
In the context of Adams spectral sequences it is conventional to depict this information graphically by
-
dots;
-
of which sequences of length are connected by vertical lines, for .
For example the graphical representation of the -primary group
is
This notation comes from the convention of drawing stable pages of multiplicative Adams spectral sequences and reading them as encoding the extension problem for computing the homotopy groups that the spectral sequence converges to:
-
a dot at the top of a vertical sequence of dots denotes the group ;
-
inductively, a dot vetically below a sequence of dots denotes a group extension of by the group represented by the sequence of dots above;
-
a vertical line between two dots means that the generator of the group corresponding to the upper dot is, regarded after inclusion into the group extension, the product by of the generator of the group corresponding to the lower dot, regarded as represented by the generator of the group extension.
So for instance
stands for an abelian group which forms a group extension of the form
such that multiplication by takes the generator of the bottom copy of , regarded as represented by the generator of , to the generator of the image of the top copy of .
This means that of the two possible choices of extensions (by example ) corresponds to the non-trivial extension . Because then in
the image of the generator 1 of the first group in the middle group is .
Conversely, the notation
stands for an abelian group which forms a group extension of the form
such that multiplication by of the generator of the top group in the middle group does not yield the generator of the bottom group.
This means that of the two possible choices (by example ) corresponds to the trivial extension . Because then in
the generator 1 of the top group maps to the element in the middle group, and multiplication of that by is instead of , where the latter is the generator of the bottom group.
Similarly
is to be read as the result of appending to the previous case a dot below, so that this now indicates a group extension of the form
such that -times the generator of the bottom group, regarded as represented by the generator of the middle group, is the image of the generator of the top group. This is again the case for the unique non-trivial extension, and hence in this case the diagram stands for .
And so on.
For example the stable page of the -classical Adams spectral sequence for computation of the 2-primary part of the stable homotopy groups of spheres has in (“internal”) degree the following non-trivial entries:
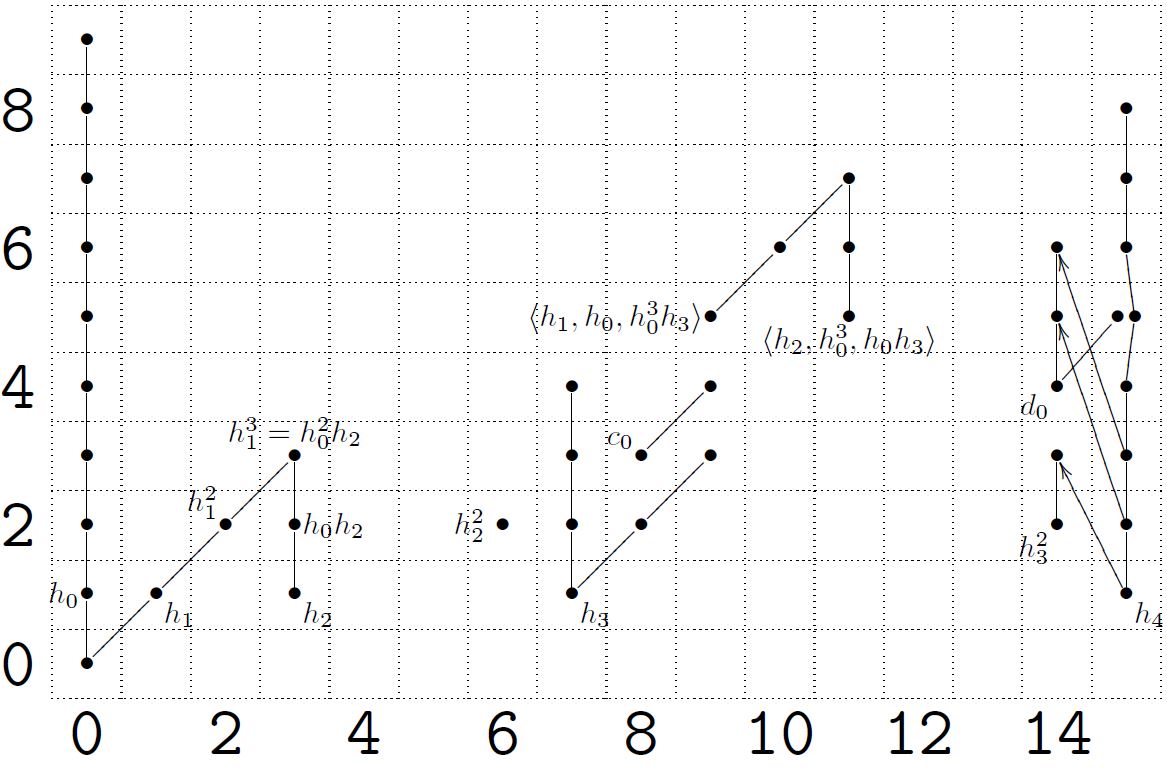
(graphics taken from (Schwede 12))
Ignoring here the diagonal lines (which denote multiplication by the element that encodes the additional ring structure on which here we are not concerned with) and applying the above prescription, we read off for instance that (because all three dots are connected) while (because here the two dots are not connected). In total
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Here the only entry that needs further explanation is the one for . We discuss the relevant concepts for this below in the section Localization and adic completion of abelian groups, but for completeness, here is the quick idea:
The symbol refers to the 2-adic integers (def. ), i.e. for the limit of abelian groups
This is not 2-primary, but it does arise when applying 2-adic completion of abelian groups (def. ) to finitely generated abelian groups as in theorem . The 2-adic integers is the abelian group associated to the diagram
as in the above figure. Namely by the above prescrption, this infinite sequence should encode an abelian group such that it is an extension of by itself of the form
(Because it is supposed to encode an extension of by the group corresponding to the result of chopping off the lowest dot, which however in this case does not change the figure.)
Localization and adic completion of abelian groups
Remark
Recall that Ext-groups between abelian groups Ab are concentrated in degrees 0 and 1 (prop.). Since
is the plain hom-functor, this means that there is only one possibly non-vanishing Ext-group , therefore often abbreviated to just “”:
Definition
Let be an abelian group.
Then an abelian group is called -local if all the Ext-groups from to vanish:
hence equivalently (remark ) if
A homomorphism of abelian groups is called -local if for all -local groups the function
is a bijection.
(Beware that here it would seem more natural to use instead of , but we do use . See (Neisendorfer 08, remark 3.2).
A homomorphism of abelian groups
is called a -localization if
-
is -local;
-
is a -local morphism.
We now discuss two classes of examples of localization of abelian groups
Classical localization at/away from primes
For , write for the cyclic group of order .
Lemma
For and any abelian group, then
-
the hom-group out of into is the -torsion subgroup of
-
the first Ext-group out of into is
Proof
Regarding the first item: Since is generated by its element 1 a morphism is fixed by the image of this element, and the only relation on 1 in is that .
Regarding the second item:
Consider the canonical free resolution
By the general discusson of derived functors in homological algebra this exhibits the Ext-group in degree 1 as part of the following short exact sequence
where the morphism on the left is equivalently .
Example
An abelian group is -local precisely if the operation
of multiplication by is an isomorphism, hence if “ is invertible in ”.
Proof
By the first item of lemma we have
By the second item of lemma we have
Hence by def. is -local precisely if
and if
Both these conditions are equivalent to multiplication by being invertible.
Definition
For a set of prime numbers, consider the direct sum of cyclic groups of order .
The operation of -localization of abelian groups according to def. is called inverting the primes in .
Specifically
-
for a single prime then -localization is called localization away from ;
-
for the set of all primes except then -localization is called localization at ;
-
for the set of all primes, then -localizaton is called rationalization..
Definition
For a set of prime numbers, then
denotes the subgroup of the rational numbers on those elements which have an expression as a fraction of natural numbers with denominator a product of elements in .
This is the abelian group underlying the localization of a commutative ring of the ring of integers at the set of primes.
If is the set of all primes except one also writes
Notice the parenthesis, to distinguish from the notation for the p-adic integers (def. below).
Remark
The terminology in def. is motivated by the following perspective of arithmetic geometry:
Generally for a commutative ring, then an -module is equivalently a quasicoherent sheaf on the spectrum of the ring .
In the present case is the integers and abelian groups are identified with -modules. Hence we may think of an abelian group equivalently as a quasicoherent sheaf on Spec(Z).
The “ring of functions” on Spec(Z) is the integers, and a point in is labeled by a prime number , thought of as generating the ideal of functions on Spec(Z) which vanish at that point. The residue field at that point is .
Inverting a prime means forcing to become invertible, which, by this characterization, it is precisely away from that point which it labels. The localization of an abelian group at hence corresponds to the restriction of the corresponding quasicoherent sheaf over to the complement of the point labeled by .
Similarly localization at is localization away from all points except .
See also at function field analogy for more on this.
Proposition
For a set of prime numbers, a homomorphism of abelian groups is local (def. ) with respect to (def. ) if under tensor product of abelian groups with (def. ) it becomes an isomorphism
Moreover, for any abelian group then its -localization exists and is given by the canonical projection morphism
(e.g. Neisendorfer 08, theorem 4.2)
Formal completion at primes
We have seen above in remark that classical localization of abelian groups at a prime number is geometrically interpreted as restricting a quasicoherent sheaf over Spec(Z) to a single point, the point that is labeled by that prime number.
Alternatively one may restrict to the “infinitesimal neighbourhood” of such a point. Technically this is called the formal neighbourhood, because its ring of functions is, by definition, the ring of formal power series (regarded as an adic ring or pro-ring). The corresponding operation on abelian groups is accordingly called formal completion or adic completion or just completion, for short, of abelian groups.
It turns out that if the abelian group is finitely generated then the operation of p-completion coincides with an operation of localization in the sense of def. , namely localization at the p-primary component of the group (def. below). On the one hand this equivalence is useful for deducing some key properties of p-completion, this we discuss below. On the other hand this situation is a shadow of the relation between localization of spectra and nilpotent completion of spectra, which is important for characterizing the convergence properties of Adams spectral sequences.
Definition
For a prime number, then the p-adic completion of an abelian group is the abelian group given by the limit
where the morphisms are the evident quotient morphisms. With these understood we often write
for short. Notice that here the indexing starts at .
Example
The p-adic completion (def. ) of the integers is called the p-adic integers, often written
which is the original example that gives the general concept its name.
With respect to the canonical ring-structure on the integers, of course is a prime ideal.
Compare this to the ring of holomorphic functions on the complex plane. For any point, it contains the prime ideal generated by (for the canonical coordinate function on ). The formal power series ring is the adic completion of at this ideal. It has the interpretation of functions defined on a formal neighbourhood of in .
Analogously, the p-adic integers may be thought of as the functions defined on a formal neighbourhood of the point labeled by in Spec(Z).
Lemma
There is a short exact sequence
Proof
Consider the following commuting diagram
Each horizontal sequence is exact. Taking the limit over the vertical sequences yields the sequence in question. Since limits commute over limits, the result follows.
We now consider a concept of -completion that is in general different from def. , but turns out to coincide with it in finitely generated abelian groups.
Definition
For a prime number, write
for the colimit (in Ab) over iterative applications of multiplication by on the integers.
This is the abelian group generated by formal expressions for , subject to the relations
Equivalently it is the abelian group underlying the ring localization .
Definition
For a prime number, then localization of abelian groups (def. ) at (def. ) is called -completion of abelian groups.
Lemma
An abelian group is -complete according to def. precisely if both the limit as well as the lim^1 of the sequence
vanishes:
and
Proof
By def. the group is -local precisely if
Now use the colimit definition (def. ) and the fact that the hom-functor sends colimits in the first argument to limits to deduce that
This yields the first statement. For the second, use that for every cotower over abelian groups there is a short exact sequence of the form
(by this lemma).
In the present case all , which is a free abelian group, hence a projective object, so that all the Ext-groups out of it vannish. Hence by exactness there is an isomorphism
This gives the second statement.
Example
For a prime number, the p-primary cyclic groups of the form are -complete (def. ).
Proof
By lemma we need to check that
and
For the first statement observe that consecutive stages of the tower compose to the zero morphism. First of all this directly implies that the limit vanishes, secondly it means that the tower satisfies the Mittag-Leffler condition (def.) and this implies that the also vanishes (prop.).
Definition
For a prime number, write
(the p-primary part of ), where from def. .
Since colimits commute over each other, this is equivalently
Theorem
For a prime number, the -localization
of an abelian group (def. , def. ), hence the -completion of according to def. , is given by the morphism
into the first Ext-group into out of (def. ), which appears as the first connecting homomorphism in the long exact sequence of Ext-groups
that is induced (via this prop.) from the defining short exact sequence
e.g. (Neisendorfer 08, p. 16)
Proposition
If is a finitely generated abelian group, then its -completion (def. , for any prime number ) is equivalently its p-adic completion (def. )
Proof
By theorem the -completion is . By def. there is a colimit
Together this implies, by this lemma, that there is a short exact sequence of the form
By lemma the lim^1 on the left is over the -torsion subgroups of , as ranges. By the assumption that is finitely generated, there is a maximum such that all torsion elements in are annihilated by . This means that the Mittag-Leffler condition (def.) is satisfied by the tower of -torsion subgroups, and hence the lim^1-term vanishes (prop.).
Therefore by exactness of the above sequence there is an isomorphism
Proposition
If is a -divisible group in that is an isomorphism, then its -completion (def. ) vanishes.
Proof
By theorem the localization morphism sits in a long exact sequence of the form
Here by def. and since the hom-functor takes colimits in the first argument to limits, the second term is equivalently the limit
But by assumption all these morphisms that the limit is over are isomorphisms, so that the limit collapses to its first term, which means that the morphism in the above sequence is an isomorphism. But by exactness of the sequence this means that .
Corollary
Let be a prime number. If is a finite abelian group, then its -completion (def. ) is equivalently its p-primary part.
Proof
By the fundamental theorem of finite abelian groups, is a finite direct sum
of cyclic groups of ordr for prime numbers and (thm.).
Since finite direct sums are equivalently products (biproducts: Ab is an additive category) this means that
By theorem the th factor here is the -completion of , and since is an isomorphism on if (because its kernel evidently vanishes), prop. says that in this case the factor vanishes, so that only the factors with remain. On these however is the identity by example .
Localization and nilpotent completion of spectra
We discuss
which are the analogs in stable homotopy theory of the construction of localization of abelian groups discussed above.
Literature: (Bousfield 79)
Localization of spectra
Definition
Let be be a spectrum. Say that
-
a spectrum is -acyclic if the smash product with is zero, ;
-
a morphism of spectra is an -equivalence if is an isomorphism in , hence if is an isomorphism in -generalized homology;
-
a spectrum is -local if the following equivalent conditions hold
(Bousfield 79, §1) see also for instance (Lurie, Lecture 20, example 4)
Proof
Notice that being -acyclic means equivalently that the unique morphism is an -equivalence.
Hence one direction of the claim is trivial. For the other direction we need to show that for to give an isomorphism on all -equivalences , it is sufficient that it gives an isomorphism on all -equivalences of the form .
Given a morphism , write for its homotopy cofiber. Then since is a triangulated category (prop.) the defining axioms of triangulated categories (def., lemma) give that there is a commuting diagram of the form
where both the top as well as the bottom are homotopy cofiber sequences. Hence applying to this diagram in yields a diagram of graded abelian groups of the form
where now both horizontal sequences are long exact sequences (prop.).
Hence if is an isomorphism, then all four outer vertical morphisms in this diagram are isomorphisms, and then the five-lemma implies that also is an isomorphism.
Hence it is now sufficient to observe that with an -equivalence, then its homotopy cofiber is -acyclic.
To see this, notice that by the tensor triangulated structure on (prop.) the smash product with preserves homotopy cofiber sequences, so that there is a homotopy cofiber sequence
But if the first morphism here is an isomorphism, then the axioms of a triangulated category (def.) imply that . In detail: by the axioms we may form the morphism of homotopy cofiber sequences
Then since two of the three vertical morphisms on the left are isomorphisms, so is the third (lemma).
Definition
Given , then an -Bousfield localization of spectra of is
-
an -local spectrum
-
an -equivalence .
We discuss now that -Localizations always exist. The key to this is the following lemma , which asserts that a spectrum being -local is equivalent to it being -null, for some “small” spectrum :
Lemma
For every spectrum there exists a spectrum such that any spectrum is -local (def. ) precisely if it is -null, i.e.
and such that
-
there exists an infinite cardinal number such that is a -CW spectrum (hence a CW spectrum (def.) with at most many cells);
-
the class of -acyclic spectra (def. ) is the class generated by under
-
the relation that if in a homotopy cofiber sequence two of the spectra are in the class, then so is the third.
(Bousfield 79, lemma 1.13 with lemma 1.14) review includes (Bauer 11, p.2,3, VanKoughnett 13, p. 8)
Proposition
For any spectrum, every spectrum sits in a homotopy cofiber sequence of the form
and natural in , such that
-
is -acyclic,
-
is -local,
(Bousfield 79, theorem 1.1) see also for instance (Lurie, Lecture 20, example 4)
Proof
Consider the -CW-spectrum spectrum whose existence is asserted by lemma . Let
denote the set containing as its single element the canonical morphism (of sequential spectra) from into the standard cone of , i.e. the cofiber
of the inclusion of into its standard cylinder spectrum (def.).
Since the standard cylinder spectrum on a CW-spectrum is a good cylinder object (prop.) this means (lemma) that for any fibrant sequential spectrum, and for any morphism, then an extension along the cone inclusion
equivalently exhibits a null-homotopy of the top morphism. Hence the -injective objects in are precisely those spectra for which .
Moreover, due to the degreewise nature of the smash tensoring (def), the inclusion morphism is degreewise the inclusion of a CW-complex into its standard cone, which is a relative cell complex inclusion (prop.).
By this lemma the -cell spectrum is -small object (def.) with respect to morphisms of spectra which are degreewise relative cell complex inclusion small object argument .
Hence the small object argument applies (prop.) and gives for every a factorization of the terminal morphism as an -relative cell complex (def.) followed by an -injective morphism (def.)
By the above, this means that , hence by lemma that is -local.
It remains to see that the homotopy fiber of is -acyclic: By the tensor triangulated structure on (prop.) it is sufficient to show that the homotopy cofiber is -acyclic (since it differs from the homotopy fiber only by suspension). By the pasting law, the homotopy cofiber of a transfinite composition is the transfinite composition of a sequence of homotopy pushouts. By lemma and applying the pasting law again, all these homotopy pushouts produce -acyclic objects. Hence we conclude by observing that the transfinite composition of the morphisms between these -acyclic objects is -acyclic. Since by construction all these morphisms are relative cell complex inclusions, this follows again with the compactness of the -spheres (lemma).
Proof
It only remains to show that is an -equivalence. By the tensor triangulated structure on (prop.) the smash product with preserves homotopy cofiber sequences, so that
is also a homotopy cofiber sequence. But now by prop. , and so the axioms (def.) of the triangulated structure on (prop.) imply that is an isomorphism.
Nilpotent completion of spectra
Definition
Let be a homotopy commutative ring spectrum (def.) and any spectrum. Write for the homotopy fiber of the unit as in def. such that the -Adams filtration of (def. ) reads (according to lemma )
For , write
for the homotopy cofiber. Here . By the tensor triangulated structure of (prop.), this homotopy cofiber is preserved by forming smash product with , and so also
Now let
be the morphism implied by the octahedral axiom of the triangulated category (def., prop.):
By the commuting square in the middle and using again the tensor triangulated structure, this yields an inverse sequence under :
The E-nilpotent completion of is the homotopy limit over the resulting inverse sequence
or rather the canonical morphism into it
Concretely, if
is presented by a tower of fibrations between fibrant spectra in the model structure on topological sequential spectra, then is represented by the ordinary sequential limit over this tower.
(Bousfield 79, top, middle and bottom of page 272)
Remark
In (Bousfield 79) the -nilpotent completion of (def. ) is denoted “”. The notation “” which we use here is more common among modern authors. It emphasizes the conceptual relation to p-adic completion of abelian groups (def. ) and is less likely to lead to confusion with the smash product of with .
Remark
The nilpotent completion is -local. This induces a universal morphism
from the -Bousfield localization of spectra of into the -nilmpotent completion
(Bousfield 79, top of page 273)
We consider now conditions for this morphism to be an equivalence.
Proposition
Let be a connective ring spectrum such that the core of , def. , is either of
-
the localization of the integers at a set of primes, ;
-
a ring of integers modulo n , for .
(Bousfield 79, theorem 6.5, theorem 6.6).
Convergence theorems
We state the two main versions of Bousfield‘s convergence theorems for the -Adams spectral sequence, below as theorem and theorem .
First we need to define the concepts that enter the convergence statement:
Broadly the statement will be that typically
-
the -Adams spectral sequence computes the stable homotopy groups of maps from into the E-nilpotent completion of ;
-
these groups are localizations of the full groups depending on the core of .
Literature: (Bousfield 79)
Definition
Let be a homotopy commutative ring spectrum (def.) and two spectra with associated -Adams spectral sequence (def. ).
Observe that
since the differential on the th page has bidegree , and since , so that for the image of in vanishes.
Thus define the bigraded abelian group
called the “infinity page” of the -Adams spectral sequence.
Definition
Let be a homotopy commutative ring spectrum (def.) and two spectra with associated -Adams spectral sequence (def. ) and E-nilpotent completion (def. ).
Define a filtration
on the graded abelian group by
Definition
Let be a homotopy commutative ring spectrum (def.) and two spectra with associated -Adams spectral sequence (def. ) and E-nilpotent completion (def. ).
Say that the -Adams spectral sequence converges completely to the E-nilpotent completion if the following two canonical morphisms are isomorphisms
-
(where on the right we have the limit over the tower of quotients by the stages of the filtration from def. )
-
(where is the filtration stage from def. and is the infinity-page from def. ).
Notice that the first morphism is always surjective, while the second is necessarily injective, hence the condition is equivalently that the first is also injective, and the second also surjective.
Now we state sufficient conditions for complete convergence of the -Adams spectral sequence. It turns out that convergence is controled by the core (def. ) of the ring . By prop. these cores are either localizations of the integers at a set of primes (def. ) or are rings of integers modulo n, or cores of products of these. We discuss the first two cases.
Theorem
Let be a homotopy commutative ring spectrum (def.) and let be two spectra such that
-
the core (def. ) of the 0-th stable homotopy group ring of (prop.) is the localization of the integers at a set of primes (def. )
-
is a CW-spectrum (def.) with a finite number of cells (rmk.);
then the -Adams spectral sequence for (def. ) converges completely (def. ) to the localization
of .
Theorem
Let be a homotopy commutative ring spectrum (def.) and let be two spectra such that
-
the core (def. ) of the 0-th stable homotopy group ring of (prop.) is a prime field
for some prime number ;
-
is a connective spectrum in that its stable homotopy groups vanish in negative degree;
-
is a CW-spectrum (def.) with a finite number of cells (rmk.);
-
is degreewise a finitely generated group
then the -Adams spectral sequence for (def. ) converges completely (def. ) to the -adic completion (def. )
of .
Examples
Example
Examples of commutative ring spectra for which the dual -Steenrod algebra over of def. where the left and right action of are not just isomorphic (via prop. ) but actually equal according to remark , includes the case H.
Example
Examples of commutative ring spectra that are flat according to def. include
-
– the sphere spectrum;
-
MO, MU, MSp – Thom spectra;
-
KO, KU – topological K-theory spectra.
(Adams 69, lecture 1, lemma 28 (p. 45))
Proof of the first two items
For we have , since the sphere spectrum is the tensor unit for the derived smash product of spectra (cor.). Hence the statement follows since every ring is, clearly, flat over itself.
For we have that (prop.), hence a field (a prime field). Every module over a field is a projective module (prop.) and every projective module is flat (prop.).
Example
-
the Eilenberg-MacLane spectrum of a prime field. For a connective spectrum, its -nilpotent completion is its p-completion
(where denotes the Moore spectrum of the abelian group ).
-
MU. Every spectrum is alreay -nilpotently complete
-
BP at prime . For every spectrum its -nilpotent completion is its p-localization
(where is the result of inverting all primes different from ).
For more discussion of E-infinity (derived) formal completions via totalizations of Amitsur complexes, see (Carlsson 07).
Classical Adams spectral sequence (, )
We consider now the example of the -Adams spectral sequence (def. ) for the case that
-
is the Eilenberg-MacLane spectrum (def.) with coefficients in a prime field, regarded in with its canonical struture of a homotopy commutative ring spectrum induced (via this corollary) from its canonical structure of an orthogonal ring spectrum (from this def.);
-
are both the sphere spectrum.
This example is called the classical Adams spectral sequence.
The -dual Steenrod algebra according to the general definition turns out to be the classical dual Steenrod algebra recalled below .
Notice that satisfies the two assumptions needed to identify the second page of the -Adams spectral sequence according to theorem :
Lemma
The Eilenberg-MacLane spectrum is flat according to , and is a projective module over .
Proof
The stable homotopy groups of is the prime field itself, regarded as a graded commutative ring concentrated in degree 0 (prop.)
Since this is a field, all modules over it are projective modules (prop.), hence in particular flat modules (prop.).
Corollary
The classical Adams spectral sequence, i.e. the -Adams spectral sequence (def. ) for (def.) and , has on its second page the Ext-groups of classical dual Steenrod algebra comodules from to itself, and converges completely (def. ) to the p-adic completion (def. ) of the stable homotopy groups of spheres, hence in degree 0 to the p-adic integers and in all other degrees to the -primary part (theorem )
Proof
By lemma the conditions of theorem are satisfied, which implies the form of the second page.
For the convergence statement, we check the assumptions in theorem :
-
By prop. and prop. the ring coincides with its core: ;
-
is clearly a connective spectrum;
-
is clearly a finite CW-spectrum;
-
the groups are degreewise finitely generated, by Serre's finiteness theorem?.
Hence theorem applies and gives the convergence as stated.
Finally, by prop. the dual -Steenrod algebra in the present case is the classical dual Steenrod algebra.
We now use the classical Adams spectral sequence from corollary to compute the first dozen stable homotopy groups of spheres.
The dual Steenrod algebra
Definition
Let be a prime number. Write for the corresponding prime field.
The mod -Steenrod algebra is the graded co-commutative Hopf algebra over which is
-
for generated by elements denoted for , ;
-
for generated by elements denoted and for ,
(called the Serre-Cartan basis elements)
whose product is subject to the following relations (called the Ádem relations):
for :
for the
for :
for then
and if then
and whose coproduct is subject to the following relations:
for :
for :
and
e.g. (Kochmann 96, p. 52)
Definition
The -linear dual of the mod -Steenrod algebra (def. ) is itself naturally a graded commutative Hopf algebra (with coproduct the linear dual of the original product, and vice versa), called the dual Steenrod algebra .
Proposition
There is an isomorphism
(e.g. Ravenel 86, p. 49, Rognes 12, remark 7.24)
We now give the generators-and-relations description of the dual Steenrod algebra from def. , in terms of linear duals of the generators for itself, according to def. .
Theorem
(Milnor’s theorem)
The dual mod -Steenrod algebra (def. ) is, as an associative algebra, the free graded commutative algebra
on generators:
-
, being the linear dual to ,
of degree .
The dual mod -Steenrod algebra (def. ) is, as an associative algebra, the free graded commutative algebra
on generators:
-
, being the linear dual to ,
of degree .
-
being linear dual to .
Moreover, the coproduct on is given on generators by
and
where we set .
(This defines the coproduct on the full algbra by it being an algebra homomorphism.)
This is due to (Milnor 58). See for instance (Kochmann 96, theorem 2.5.1, Ravenel 86, chapter III, theorem 3.1.1)
The cobar complex
In order to compute the second page of the classical -Adams spectral sequence (cor. ) we consider a suitable cochain complex whose cochain cohomology gives the relevant Ext-groups.
Definition
Let be a graded commutative Hopf algebra, hence a commutative Hopf algebroid for which the left and right units coincide (remark ).
Then the unit coideal of is the cokernel
Remark
By co-unitality of graded commutative Hopf algebras (def. ) the defining projection of the unit coideal (def. )
forms a split exact sequence which exhibits a direct sum decomposition
Lemma
Let be a commutative Hopf algebra, hence a commutative Hopf algebroid for which the left and right units coincide .
Then the unit coideal (def. ) carries the structure of an -bimodule such that the projection morphism
is an -bimodule homomorphism. Moreover, the coproduct descends to a morphism such that the projection intertwines the two coproducts.
Proof
For the first statement, consider the commuting diagram
where the left commuting square exhibits the fact that is a homomorphism of left -modules.
Since the tensor product of abelian groups is a right exact functor it preserves cokernels, hence is the cokernel of and hence the right vertical morphisms exists by the universal property of cokernels. This is the compatible left module structure on . Similarly the right -module structure is obtained.
For the second statement, consider the commuting diagram
Here the left square commutes by one of the co-unitality conditions on , equivalently this is the co-action property of regarded canonically as a -comodule.
Since also the bottom morphism factors through zero, the universal property of the cokernel implies the existence of the right vertical morphism as shown.
Definition
(cobar complex)
Let be a commutative Hopf algebra, hence a commutative Hopf algebroid for which the left and right units coincide . Let be a left -comodule.
The cobar complex is the cochain complex of abelian groups with terms
(for the unit coideal of def. , with its -bimodule structure via lemma )
and with differentials given by the alternating sum of the coproducts via lemma .
Proposition
Let be a commutative Hopf algebra, hence a commutative Hopf algebroid for which the left and right units coincide . Let be a left -comodule.
Then the cochain cohomology of the cobar complex (def. ) is the Ext-groups of comodules from (regarded as a left comodule via def. ) into
(Ravenel 86, cor. A1.2.12, Kochman 96, prop. 5.2.1)
Proof idea
One first shows that there is a resolution of by co-free comodules given by the complex
with differentials given by the alternating sum of the coproducts. This is called the cobar resolution of .
To see that this is indeed a resolution, one observes that a contracting homotopy is given by
for and
Now from lemma , in view of remark , and since is trivially projective over itself, it follows that this is an -acyclic resolution for .
This means that the resolution serves to compute the Ext-functor in question and we get
where the second-but-last equivalence is the isomorphism of the co-free/forgetful adjunction
from prop. , while the last equivalence is the isomorphism of the free/forgetful adjunction
The May spectral sequence
The cobar complex (def. ) realizes the second page of the classical Adams spectral sequence (cor. ) as the cochain cohomology of a cochain complex. This is still hard to compute directly, but we now discuss that this cochain complex admits a filtration so that the induced spectral sequence of a filtered complex is computable and has trivial extension problem (rmk.). This is called the May spectral sequence.
We obtain this spectral sequence in prop. below. First we need to consider some prerequisites.
Lemma
Let be a graded commutative Hopf algebra, i.e. a graded commutative Hopf algebroid with left and right unit coinciding for which the underlying -algebra of is a free graded commutative -algebra on a set of generators
such that
-
all generators are primitive elements;
-
is in degree 0;
-
;
-
there are only finitely many in a given degree,
then the Ext of -comodules from to itself is the free graded commutative algebra on these generators
(Ravenel 86, lemma 3.1.9, Kochman 96, prop. 3.7.5)
Proof
Consider the co-free left -comodule (prop.)
and regard it as a chain complex of left comodules by defining a differential via
and extending as a graded derivation.
We claim that is a homomorphism of left comodules: Due to the assumption that all the are primitive we have on generators that
and
Since is a graded derivation on a free graded commutative algbra, and is an algebra homomorphism, this implies the statement for all other elements.
Now observe that the canonical chain map
(which projects out the generators and and is the identity on ), is a quasi-isomorphism, by construction. Therefore it constitutes a co-free resolution of in left -comodules.
Since the counit is assumed to be flat, and since is degreewise a free module over , hence in particular a projective module, prop. says that the above is an acyclic resolution with respect to the functor . Therefore it computes the Ext-functor. Using that forming co-free comodules is right adjoint to forgetting -comodule structure over (prop. ), this yields:
Lemma
If as above is equipped with a filtering, then there is a spectral sequence
converging to the Ext over from to itself, whose first page is the over the associated graded Hopf algebra .
(Ravenel 86, lemma 3.1.9, Kochman 96, prop. 3.7.5)
Proof
The filtering induces a filtering on the cobar complex (def. ) which computes (prop. ). The spectral sequence in question is the corresponding spectral sequence of a filtered complex. Its first page is the homology of the associated graded complex (by this prop.), which hence is the homology of the cobar complex (def. ) of the associated graded Hopf algebra . By prop. this is the Ext-groups as shown.
Let now , be the mod 2 dual Steenrod algebra. By Milnor's theorem (prop. ), as an -algebra this is
and the coproduct is given by
where we set .
Definition
Introduce new generators
Remark
By binary expansion of powers, there is a unique way to express every monomial in as a product of the new generators in def. such that each such element appears at most once in the product. E.g.
Proposition
In terms of the generators from def. , the coproduct on the dual Steenrod algebra takes the following simple form
Proof
Using that the coproduct of a bialgebra is a homomorphism for the algebra structure and using freshman's dream arithmetic over , one computes:
Proposition
There exists a converging spectral sequence of graded -vector spaces of the form
called the May spectral sequence (where and are from the bigrading of the spectral sequence itself, while the index is that of the graded -vector spaces), with
-
first differential given by
-
higher differentials of the form
where the filtration is by maximal degree.
Notice that since everything is -linear, the extension problem of this spectral sequence is trivial.
Proof
Define a grading on the dual Steenrod algebra (theorem ) by taking the degree of the generators from def. to be (this idea is due to (Ravenel 86, p.69))
and extending this additively to monomials, via the unique decomposition of remark .
For example
Consider the corresponding increasing filtration
with filtering stage containing all elements of total degree .
This means that after projection to the associated graded Hopf algebra
all the generators become primitive elements:
Hence lemma applies and says that the from to itself over the associated graded Hopf algebra is the polynomial algebra in these generators:
Moreover, lemma says that this is the first page of a spectral sequence that converges to the over the original Hopf algebra:
Moreover, again by lemma , the differentials on any -page are the restriction of the differentials of the bar complex to the -almost cycles (prop.). Now the differential of the cobar complex is the alternating sum of the coproduct on , hence by prop. this is:
The second page
Now we use the May spectral sequence (prop. ) to compute the second page and in fact the stable page of the classical Adams spectral sequence (cor. ) in low internal degrees .
Lemma
(terms on the second page of May spectral sequence)
In the range , the second page of the May spectral sequence for has as generators all the
as well as the element
subject to the relations
-
.
e.g. (Ravenel 86, lemma 3.2.8 and lemma 3.2.10, Kochman 96, lemma 5.3.2)
Proof
Remember that the differential in the cobar complex (def. ) lands not in itself, but in the unit coideal where the generator disappears.
Using this we find for the differential of the generators in low degree on the first page of the May spectral sequence (prop. ) via the formula for the differential from prop. , the following expressions:
and hence all the elements are cocycles on the first page of the May spectral sequence.
Also, since is a derivation (by definition of the cobar complex, def. ) and since the product of the image of the cobar complex in the first page of the May spectral sequence is graded commutative, we have for all that
(since ).
Similarly we compute on the other generators. These terms do not vanish, but so they impose relations on products in the cobar complex:
This shows that in the given range.
The remaining statements follow similarly.
Remark
With lemma , so far we see the following picture in low degrees.
Here the relation
removes a vertical tower of elements above .
So far there are two different terms in degree . The next lemma shows that these become identified on the next page.
Lemma
(differentials on the second page of the May spectral sequence)
The differentials on the second page of the May spectral sequence (prop. ) relevant for internal degrees are
Proof
The first point follows as before in lemma , in fact the are infinite cycles in the May spectral sequence.
We spell out the computation for the second item:
We may represent by plus terms of lower degree. Choose the representative
Then we compute , using the definition of the cobar complex (def. ), the value of the coproduct on dual generators (theorem ), remembering that the coproduct on a Hopf algebra is a homomorphism for the underlying commutative ring, and using freshman's dream arithmetic to evaluate prime-2 powers of sums. For the three summands we obtain
and
and
The labeled summands appear twice in hence vanish (mod 2). The remaining terms are
and these indeed represent the claimed elements.
Remark
With lemma the picture from remark is further refined:
For the differentia means that on the third page of the May spectral sequence there is an identification
Hence where on page two we saw two distinct elements in bidegree , on the next page these merge:
Proceeding in this fashion, one keeps going until the 4-page of the May spectral sequence (Kochman 96, lemma 5.3.5). Inspection of degrees shows that this is sufficient, and one obtains:
Theorem
(stable page of classical Adams spectral sequence)
In internal degree the infinity page (def. ) of the classical Adams spectral sequence (cor. ) is spanned by the items in the following table

Here every dot is a generator for a copy of . Vertical edges denote multiplication with and diagonal edges denotes multiplication with .
e.g. (Ravenel 86, theorem 3.2.11, Kochman 96, prop. 5.3.6), graphics taken from (Schwede 12))
The first dozen stable stems
Theorem gives the stable page of the classical Adams spectral sequence in low degree. By corollary and def. we have that a vertical sequence of dots encodes an 2-primary part of the stable homotopy groups of spheres according to the graphical calculus of remark (the rules for determining group extensions there is just the solution to the extension problem (rmk.) in view of def. ):
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
The full answer in this range turns out to be this:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
And expanding the range yields this :

(graphics taken from Hatcher’s website)
-injective resolutions
A streamlined discussion of -Adams resolutions in close analogy to injective resolutions in homological algebra was given in (Miller 81), advertized in (Hopkins 99) and worked out in more detail in (Aramian).
Notice that the standard concept of exact sequences and injective objects makes sense in abelian categories, but not in the stable homotopy category of spectra, as the latter is only an additive category. Of course this is because the stable homotopy theoretic analog of what are exact sequences in abelian categories are homotopy fiber sequences of spectra. But for computational purposes it turns out useful to consider a blend between these two concepts (due to Miller 81), where a sequence of spectra is regarded as exact if the homotopical functor to the abelian category of abelian groups that it represents takes values in exact sequences. With respect to this hybrid concept, -Adams resolutions in the stable homotopy category are the direct analog of injective resolutions in an abelian category.
Definition
For a spectrum, we say that the homotopical functor that it co-represents is the functor of stable homotopy groups of the mapping spectrum-construction out of , regarded as a functor on the stable homotopy category:
(Regarded as an (∞,1)-functor on the stable (∞,1)-category of spectra this is also called the homological functor co-represented by .)
Example
For the sphere spectrum then the homotopical functor that it co-represents according to def.
is the stable homotopy group-functor.
Throughout, is a ring spectrum.
Definition
Say that
-
a sequence of spectra
is
-
a (long) exact sequence if the induced sequence of homotopy functors according to def. , is a long exact sequence in ;
-
(for ) a short exact sequence if
is (long) exact in the above sense;
-
-
a morphism is
-
a monomorphism if is an exact sequence in the above sense;
-
an epimorphism if is an exact sequence in the above sense.
-
For a ring spectrum, then a sequence of spectra is called (long/short) -exact and a morphism is epi/mono, respectively, if becomes long/short exact or epi/mono, respectively, after taking smash product with .
Example
Every homotopy cofiber sequence of spectra is exact in the sense of def. .
Example
The suspension functor preserves exact sequences in the sense of def. .
Proof
By the suspension/looping adjunction-isomorphism (prop.) and so the statement follows from the assumption that is long exact.
Example
If a morphism, has a retraction in Ho(Spectra) then it is a monomorphism in the sense of def. .
Proof
We need to check that for every the morphism is surjective. By retraction, given , then is a preimage.
Proof
We need to check that is a monomorphism in the sense of def. . Observe that this morphism has a retraction given by . Therefore it is a monomorphism by example .
Remark/Warning
Consecutive morphisms in an -exact sequence according to def. in general need not compose up to homotopy, to the zero morphism. But this does become true (lemma below) for sequences of -injective objects, defined below in def. .
Lemma
-
If is a monomorphism in the sense of def. , then there exists a morphism such that the wedge sum morphism is a weak homotopy equivalence
In particular, every morphism in Ho(Spectra) has an extension along a monomorphism in this sense.
-
If is an epimorpimsm in the sense of def. , then there exists a homotopy section , i.e. , together with a morphism such that the wedge sum morphism is a weak homotopy equivalence
Proof
Given a monomorphism , consider the correspondiing homotopy cofiber sequence
We first observe that the connecting homomorphism is equivalent to the zero morphism . This follows because by example the sequence
is an exact sequence (of homotopy groups) for every , while by example the morphism on the right is epi, so that .
Now since is also a homotopy fiber sequence, the pasting law identifies :
Definition
For a ring spectrum, say that a spectrum is -injective if for each morphism and each -monomorphism in the sense of def. , there is a diagram in HoSpectra of the form
Lemma
A spectrum is -injective in the sense of def. , precisely if it is a retract in HoSpectra of a free -modules, hence of for some spectrum .
Proof
In one direction, assume that is -injective and consider the diagram
By example here the vertical morphism is an -monomorphism, and so by assumption there is a lift
which exhibits as a retract of .
In the other direction, given a retraction we show that there exist extensions in
whenever the vertical morphism is an -monomorphism. To see this, complete the extension problem to the following commuting diagram
Now, since is assumed to be an -monomorphism, the morphism on the right is a monomorphism in the sense of def. , and so by lemma there exists an extension in
By composition and commutativity, this gives the required extension of along .
Definition
For a ring spectrum, then an -Adams resolution of an spectrum is a long exact sequence, in the sense of def. , of the form
Lemma
Any two consecutive maps in an -Adams resolution, def. , compose to the zero morphism.
The following lemma says that -Adams resolutions may be extended along morphisms.
Lemma
For an -Adams resolution, def. , and for any morphism, then there exists an -Adams resolution and a commuting diagram
There are two -Adams resolutions that we will consider. Following (Hopkins 99) we call them the “normalized resolution” and the “standard resolution”. But beware that what all the traditional literature (Adams 74, Bousfield 79, Ravenel 86, …) considers (and somewhat implicitly) is the “normalized” resolution, not the standard resolution. The standard resolution is standard only from the more recent perspective of E-∞ geometry: it is the Amitsur complex of the -algebra , exhibiting the formal dual of the Cech nerve of .
Example
(normalized -Adams resolution)
Let denote the homotopy fiber of the unit of the ring spectrum , fitting into a homotopy fiber sequence
For a spectrum, its normalized -Adams resolution is the top row of
(e.g. Hopkins 99, corollary 5.3).
Remark
The notation for in def. follows (Bousfield 79, section 5). In (Hopkins 99, proof of corollary 5.3) the same notation is used not for the homotopy fiber of but for its homotopy cofiber. While our notation makes plenty of “”s appear in the above resolution, the advantage is that in the induced inverse sequence of a normalized resolution below in example these all drop out and we are left with the original form of the expressions as considered by (Adams 74) and followed in most of the literature.
Example
(standard -Adams resolution)
Any ring spectrum gives rise to an augmented cosimplicial spectrum (its bar construction)
whose
-
coface maps are given by inserting the unit
-
codegeneracy maps are given by the product operation
The corresponding Amitsur complex is given by forming alternating sums of the coface maps
Given any spectrum , then forming the smash product with this sequence yields a sequence of the form
This is called the standard -Adams resolution of .
(e.g. Hopkins 99, def. 5.4).
Proposition
The standard resolution of example is indeed an -Adams resolution of in the sense of def. .
Proof
As generally for bar resolutions, one checks that the alternating sum of the codegeneracy maps constitute homotopy operators that give contracting homotopies when commuted with the alternating sum of the coface maps. This gives that the sequence is -exact. Moreover, the terms in the sequence are all -injective by lemma .
-Adams towers
Definition
An -Adams tower of a spectrum is a commuting diagram in the stable homotopy category of the form
such that
-
each hook is a homotopy fiber sequence;
-
the composition of the -adjuncts of with
Call this the associated -Adams resolution of the -Adams tower.
The following is the main statement of the above little theory of -injective spectra.
Proposition
Every -Adams resolution (def. ) induces an -Adams tower, def. of which it is the associated -Adams resolution.
Proof idea
Given an -Adams resolution
consider the induced diagram
constructed inductively as follows:
To start with, is the homotopy cofiber of , and is the morphism universally induced from this by the fact that , by lemma . Observe that is an -monomorphism and is an -epimorphism in the sense of def. .
Then assume that an -epi/mono factorization
has been constructed. Let now be its homotopy cofiber. Since is -epi, the equivalence from lemma implies that already . With this, the universal property of the homotopy cofiber induces a morphism . As before, is -epi and is -mono, and so the induction proceeds.
Using this, we now construct an -Adams tower as follows (…).
There is another tower associated with an -Adams resolutions:
Example
Let be a normalized -Adams resolution according to example . Then its associated inverse sequence according to def. is the sequence from def.
This is the tower of spectra considered in the original texts (Adams 74, p. 318) and (Bousfield 79, p. 271).
Remark
In (Ravenel 84, p. 356) it is the associated inverse sequence as in example that is called the “Adams tower”, while in (Ravenel 86, def. 2.21) this is called an “-Adams resolution”. We instead follow (Hopkins 99) in using “-Adams resolution” for “-injective resolution” as in def. , “-Adams tower” for def. and follow (Aramian) in saying “associated inverse sequence” for the above.
-Adams spectral sequences
Definition
Given spectra and , and given an -Adams resolution of , def. , or equivalently (by prop. ) an -Adams tower over , def. ,
then the corresponding -Adams spectral sequence for the mapping spectrum is the associated spectral sequence of a tower of fibrations of the image of that tower of fibrations under the mapping spectrum operation :
More in detail, the associated exact couple of the tower is
with
and
The -Adams spectral sequence of the -Adams tower is the spectral sequence induced by this exact couple.
Proposition
Given two -Adams towers, def. , for some , then the corresponding two -Adams spectral sequences, def. , are isomorphic from the -page on.
Proposition
Given an -Adams resolution (def. ), there is an isomorphism of spectral sequences between
-
the tower spectral sequence of its associated -Adams tower (def. ), i.e. the spectral sequence of def. ;
-
the tower spectral sequence of its associated inverse sequence (def. ).
Remark
Hence both of these construction are to be called the -Adams spectral sequence. It is in fact the second construction – for the case of the normalized resolution as in example – that is considered in the original sources (Adams 74, p. 318, Bousfield 79, p. 271).
As derived descent in -geometry
It turns out that the E-nilpotent completion according to Bousfield‘s original definition – to which the -Adams spectrum seequence converges under good conditions (theorem , theorem ) – is equivalently the homotopy limit over the tower of totalizations of the canonical cosimplicial spectrum (prop.).
This means that the -Adams spectral sequence may equivalently be regarded as computing descent of quasicoherent infinity-stacks in E-infinity geometry along the canonical morphisms Spec(S).
This perspective seems to originate in (Hopkins 99, remark 5.5 (ii)) and is greatly expanded on in (Lurie 10, lectures 8, 9). Exposition of the basic idea is in Mathew 12 and with more details in (Wilson 13). The first published proof of the equivalence of this new perspective to the Adams-Bousfield theory is (Mathew-Naumann-Noel 15, prop. 2.14).
We give a survey here.
under construction
First we recall
for the general case of filtered objects in suitable stable (∞,1)-categories. Then we consider the specialization of that to the
Finally we consider specifically the examples of such given by
In conclusion this yields for each suitable E-∞ algebra over and -∞-module a spectral sequence converging to the homotopy groups of the -localization of , and this is
The quick idea is this: Given an -module , regard it as a quasicoherent sheaf on . Choose a map . This is a cover of its 1-image , which is the derived formal completion of at the image of . Restrict attention then to the restriction of to that formal completion . (So if was already an atlas, hence was already complete, we stick with the original ). Then pull back to the Cech nerve of the cover . The realization of this Cech nerve reproduces the completed image, and hence the canonical filtration on the Cech nerve gives a filtration spectral sequence for .
Spectral sequences computing homotopy groups of filtered objects
Let thoughout be a stable (∞,1)-category equipped with a t-structure such that its heart is an abelian category.
Definition
A generalized filtered object in is simply a sequential diagram
Or rather, the object being filtered is the homotopy limit
and the sequential diagram exhibits the filtering.
This appears as (Higher Algebra, def. 1.2.2.9).
Definition
For a generalized filtered object , def. , write
for the homotopy fiber of the th structure map, for all , and define an exact couple
where the maps are given by the long exact sequences of homotopy groups
We now have the spectral sequence of a filtered stable homotopy type.
Proposition
Let be a stable (∞,1)-category equipped with a t-structure such that its heart is an abelian category.
If has sequential limits and if for all then the spectral sequence induced by the exact couple of def. converges to the homotopy groups of the homotopy limit of the generalized filtered object:
This is due to (Higher Algebra, prop. 1.2.2.14). Review is in (Wilson 13, theorem 1.2.1).
For the traditional statement in the category of chain complexes see at spectral sequence of a filtered complex.
Homotopy groups of cosimplicial totalizations filtered by coskeleta
Definition
Given an cosimplicial object
its totalization is filtered, def. , by the totalizations of its coskeleta
Proposition
The filtration spectral sequence, prop. , applied to the filtration of a totalization by coskeleta as in def. , has as -term the cohomology groups of the Moore complex associated with the cosimplicial object
This is (Higher Algebra, remark 1.2.4.4). Review is around (Wilson 13, theorem 1.2.4).
Canonical cosimplicial resolution of -algebras
We discuss now the special case of coskeletally filtered totalizations coming from the canonical cosimplicial objects induced from E-∞ algebras (“Amitsur complexes”, “Sweedler corings”).
In this form this appears as (Lurie 10, theorem 2). A review is in (Wilson 13, 1.3). For the analog of this in the traditional formulation see (Ravenel 86, ch. 3, prop. 3.1.2).
Definition
Let be an E-∞ ring and let be an E-∞ algebra over , hence an E-∞ ring equipped with a homomorphism
The canonical cosimplicial object associated to this (the “-Sweedler coring” or “Amitsur complex”) is that given by the iterated smash product/tensor product over :
More generally, for an -∞-module, the canonical cosimplicial object is
Proposition
If is such that the self-generalized homology (the dual -Steenrod operations) is such that as a module over it is a flat module, then there is a natural equivalence
Remark
This makes be the Hopf algebroid formed by the -Steenrod algebra. See there for more on this.
Example
The condition in prop. is satisfied for
-
an Eilenberg-MacLane spectrum with coefficients;
It is NOT satisfied for
-
.
Remark
Under good conditions (…), of the canonical cosimplicial object provides a resolution of comodule tensor product and hence computes the Ext-groups over the Hopf algebroid:
(…)
Here the homotopy groups are expressed by Ext-groups using a universal coefficient theorem for generalized cohomology (Adams 74, III.13).
(e.g. Wilson 13, theorem 1.3.5, based on Bousfield 79)
Remark
There is a canonical map
from the -Bousfield localization of spectra of into the totalization.
The -Adams-Novikov spectral sequence
Summing this up yields the general -Adams(-Novikov) spectral sequence
Corollary
Let a connective E-∞ ring that satisfies the conditions of prop. . Then by prop. and prop. there is a strongly convergent multiplicative spectral sequence
converging to the homotopy groups of the -localization of . If moreover the dual -Steenrod algebra is flat as a module over , then, by prop. and remark , the -term of this spectral sequence is given by the Ext-groups over the -Steenrod Hopf algebroid.
Related concepts
References
General
The original sources are
-
Frank Adams, On the structure and applications of the Steenrod algebra, Comm. Math. Helv. 32 (1958), 180–214.
-
Sergei Novikov, The methods of algebraic topology from the viewpoint of cobordism theories, Izv. Akad. Nauk. SSSR. Ser. Mat. 31 (1967), 855–951 (Russian). (Novikov67)
-
John Frank Adams, Stable homotopy and generalized homology, Chicago Lectures in mathematics, 1974
based in parts on
- John Frank Adams, Lectures on generalised cohomology, in Peter Hilton (ed.) Category Theory, Homology Theory and Their Applications III, volume 99 of Lecture Notes in Mathematics (1969), Springer-Verlag Berlin-Heidelberg-New York.
The spectrum-level discussion of the Adams spectral sequence goes back to around
- R. M. F. Moss, On the composition pairing of Adams spectral sequences, Proceedings of the London Mathematical Society 3.1 (1968): 179-192.
The general convergence theorems are due to
-
Aldridge Bousfield, The localization of spectra with respect to homology, Topology 18 (1979), no. 4, 257–281. (pdf)
-
Douglas Ravenel, Localization with respect to certain periodic homology theories, American Journal of Mathematics, Vol. 106, No. 2, (Apr., 1984), pp. 351-414 (pdf)
based on
- Aldridge Bousfield, Daniel Kan, The core of a ring, Journal of Pure and Applied Algebra, Volume 2, Issue 1, April 1972, Pages 73-81
A streamlined presentation of Adams resolutions and their invariance properties, close in spirit to the theory of injective resolutions in homological algebra was given in
- Haynes Miller, On relations between Adams spectral sequences, with an application to the stable homotopy of a Moore space, J. Pure Appl. Algebra 20 (1981) (pdf)
further highlighted in
- Mike Hopkins, section 5 of Complex oriented cohomology theories and the language of stacks, course notes 1999 (pdf)
and worked out in some more detail in
- Nersés Aramian, The Adams spectral sequence (pdf)
For full details of some of the steps involved see also (Schwede 12).
Reviews of the traditional theory:
-
Douglas Ravenel, A Novice’s guide to the Adams-Novikov spectral sequence, in: Michael Barratt, Mark Mahowald (eds.) Geometric Applications of Homotopy Theory II. Lecture Notes in Mathematics, vol 658, Springer 1978 (doi:10.1007/BFb0068728, pdf)
-
Doug Ravenel, Complex cobordism and stable homotopy groups of spheres, 1986 onwards
-
Stanley Kochman, section 3.6 of: Bordism, Stable Homotopy and Adams Spectral Sequences, AMS 1996
-
John McCleary, chapter 9 of: A user’s guide to spectral sequences, Cambridge University Press, 2001
-
Paul Goerss, The Adams-Novikov spectral sequence and the Homotopy Groups of Spheres, lecture notes 2007 (pdf)
-
Alan Hatcher, Spectral sequences in algebraic topology II: The Adams spectral sequence (pdf)
-
Robert Bruner, An Adams spectral sequence primer, 2009 (pdf)
-
Stefan Schwede, chapter II, section 10.3 of Symmetric spectra, 2012
-
John Rognes, The Adams spectral sequence (following Bruner 09), 2012 (pdf)
-
Agnès Beaudry, Jonathan A. Campbell, §4 in: A Guide for Computing Stable Homotopy Groups, in Topology and Quantum Theory in Interaction, Contemporary Mathematics 718, Amer. Math. Soc. (2018) [arXiv:1801.07530, ams:conm/718]
(with an eye towards functorial quantum field theory)
The modern point of view in terms of derived -descent is hinted at in (Hopkins 99, remark 5.5 (ii)) and is consistently adopted in
-
Jacob Lurie, Chromatic Homotopy Theory (2010)
based on
This is nicely surveyed in
-
Akhil Mathew, The Adams spectral sequence as derived descent, and chromotopy, 2012
-
Dylan Wilson, Spectral Sequences from Sequences of Spectra: Towards the Spectrum of the Category of Spectra, lecture at 2013 Pre-Talbot Seminar, March 2013 (pdf)
The actual proof that this new perspecive is equivalent the original Adams-Bousfield theory appears as prop. 2.14 in
- Akhil Mathew, Niko Naumann, Justin Noel, Nilpotence and descent in equivariant stable homotopy theory, Advances in Mathematics Volume 305, 10 January 2017, Pages 994-1084 (arXiv:1507.06869, doi:10.1016/j.aim.2016.09.027)
Hopf algebroid -structure on
-
appendix A.1 of Ravenel 86
-
Andrew Baker, Brave new Hopf algebroids and the Adams spectral sequence for -modules (pdf)
-
Andrew Baker, Andrey Lazarev, On the Adams Spectral Sequence for -modules, Algebr. Geom. Topol. 1 (2001) 173-199 (arXiv:math/0105079)
-
Andrew Baker and Alain Jeanneret, Brave new Hopf algebroids and extensions of -algebras, Homology Homotopy Appl. Volume 4, Number 1 (2002), 163-173. (Euclid)
-
Mark Hovey, Homotopy theory of comodules over a Hopf algebroid (arXiv:math/0301229)
Further examples with more general coefficients
For tmf:
-
Mark Behrens, The Adams spectral sequence for (pdf)
-
Michael Hill, The 3-local -homology of , Proceedings of the AMS, 2007 (pdf)
Last revised on June 3, 2025 at 14:17:43. See the history of this page for a list of all contributions to it.