nLab adjunction

This page is about adjunctions in general 2-categories. Specifically for the common case of adjunctions in Cat see at adjoint functors. For the notion of “adjunction of a set to a field” in field theory, see field extension.

Idea

A pair of 1-morphisms in a 2-category form an adjunction if they are dual to each other (Lambek (1982), cf. here) in a precise sense.

There are two archetypical classes of examples:

• If $A$ is a monoidal category and $\mathbf{B}A$ denotes the one-object 2-category whose single hom-category is $A$ (the delooping of $A$), then the notion of adjoint morphisms in $\mathbf{B}A$ coincides precisely with the notion of dual objects in $A$, subsuming, in turn, classical examples such as dual vector spaces in the case that $A =$ FinDimVect.

• Adjunctions in the 2-category Cat of categories are adjoint functors.

  • Notice that essentially everything that makes category theory nontrivial and interesting, beyond groupoid-theory, is governed by the concept of adjoint functors. In particular universal constructions such as limits and colimits, Kan extensions, (co)ends are examples of adjunctions in Cat.

  • Similarly, for $V$ any cosmos for enrichment, adjunctions in the 2-category VCat of $V$-enriched categories are equivalently enriched adjoint functors. Already in simple cases such $V =$ truth values this subsumes classical concepts such as that of Galois connections.

  • Remarkably, even adjunctions in the homotopy 2-category of $(\infty,1)$-categories are equivalent to adjoint $\infty$-functors, see the examples below.

  These classes of examples make adjunctions a key notion in formal category theory.

Finally, the notion of adjunction may usefully be thought of as a generalization of the notion of equivalence in a 2-category: an adjoint 1-morphism need not be invertible (even up to 2-isomorphism) but it does have, in a precise sense, a left inverse from below or a right inverse from above.

If an adjoint 1-morphisms happens to be a genuine equivalence in a 2-category, then the adjunction is called an adjoint equivalence.

Definition

Definition

An adjunction in a 2-category is

• a pair of objects $C$ and $D$

• a pair of 1-morphisms

  $L \colon C \longrightarrow D$ (the left adjoint)

  $R \colon D \longrightarrow C$ (the right adjoint)

• a pair of 2-morphisms

  $\eta \colon 1_C \longrightarrow R \circ L$ (the adjunction unit)

  $\epsilon \colon L \circ R \longrightarrow 1_D$ (the adjunction counit)

such that the following equivalent conditions hold:

• triangle identity the following diagrams commute in the hom-categories (where “$\cdot$” denotes whiskering):

• zig-zag law the following equality of 2-morphisms:

In terms of string diagrams the above data entering the definition looks like

                          

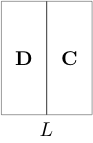
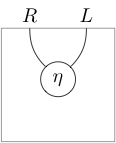
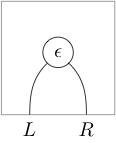
(where 1-cells read from right to left and 2-cells from bottom to top), and the zig-zag identities appear as moves “pulling zigzags straight” (hence the name):

        

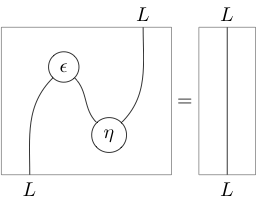
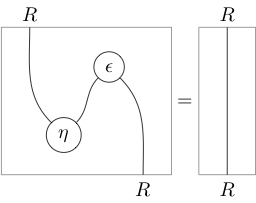
Often, arrows on strings are used to distinguish $L$ and $R$, and most or all other labels are left implicit; so the zigzag identities, for instance, become:

        

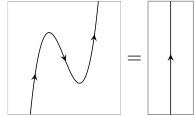
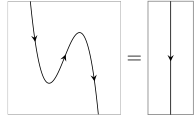
Properties

Relation to monads

See at monad – Relation between adjunctions and monads.

Examples

Adjoint functors

Proposition

An adjunction in the 2-category Cat of categories, functors and natural transformations is equivalently a pair of adjoint functors.

See also the proof here at adjoint functor.

Proof

Suppose given functors $L \,\colon\, C \to D$, $R: D \to C$ and the structure of a pair of adjoint functors in the form of a natural isomorphism of hom-sets (here)

$$\Psi_{c, d} \;\colon\; \hom_D(L(c), d) \cong \hom_C(c, R(d))$$

Now the idea is that, in the spirit of the (proof of the) Yoneda lemma, we would like $\Psi$ to be determined by what it does to identity morphisms. With that in mind, define the adjunction unit $\eta \colon 1_C \to R L$ by the formula $\eta_c = \Psi_{c, L(c)}(1_{L(c)})$. Dually, define the counit $\varepsilon \,\colon\, L R \to 1_D$ by the formula

$$\varepsilon_d \,\coloneqq\, \Psi^{-1}_{R(d), d}(1_{R(d)}) \,.$$

Then given $g \,\colon\, L(c) \to d$, the claim is that

$$\Psi_{c, d}(g) \,=\, (c \stackrel{\eta_c}{\to} R(L(c)) \stackrel{R(g)}{\to} R(d)) \,.$$

This may be left as an exercise in the yoga of the Yoneda lemma, applied to $\hom_D(L(c), -) \to \hom_C(c, R(-))$. By formal duality, given $f \,\colon\, c \to R(d)$,

$$\Psi^{-1}_{c, d}(f) = (L(c) \stackrel{L(f)}{\to} L(R(d)) \stackrel{\varepsilon_d}{\to} d) \,.$$

(We spell out the Yoneda-lemma proof of this dual form below.)

Finally, these operations should obviously be mutually inverse, but that can again be entirely encapsulated Yoneda-wise in terms of the effect on identity maps. Thus, if $\eta_c \coloneqq \Psi_{c, L(c)}(1_{L(c)})$, via the recipe just given for $\Psi^{-1}$ we recover

$$1_{L(c)} = (L(c) \stackrel{L(\eta_c)}{\to} L R L(c) \stackrel{\varepsilon_{L(c)}}{\to} L(c))$$

and this is one of the famous triangle identities: $1_L = (L \stackrel{L \eta}{\to} L R L \stackrel{\varepsilon L}{\to} L)$. Here, juxtaposition of functors and natural transformations denotes neither functor application, nor vertical composition, nor horizontal composition, but whiskering. By duality, we have the other triangle identity $1_R = (R \stackrel{\eta R}{\to} R L R \stackrel{R \varepsilon}{\to} R)$. These two triangular equations are enough to guarantee that the recipes for $\Psi$ and $\Psi^{-1}$ indeed yield mutual inverses.

In conclusion it is perfectly sufficient to define an adjoint pair of functors in $Cat$ as given by unit and counit transformations $\eta: 1_C \to R L$, $\varepsilon: L R \to 1_D$, satisfying the triangle identities above.

Remark

The definition of adjunctions via units and counits is an “elementary” definition (so that by implication, the formulation in terms of hom-isomorphismsunctor#InTermsOfHomIsomorphism) is not elementary) in the sense that while the hom-functor formulation relies on some notion of hom-*set*, the formulation in terms of units and counits is purely in the first-order language of categories and makes no reference to a model of set theory. The definition via (co)units therefore gives us a definition of adjunctions even if an assumption of local smallness is not made.

Proof

(Yoneda-lemma argument)
We claim that $\Psi^{-1}_{c, d} \,\colon\, \hom_C(c, R(d)) \to \hom_D(L(c), d)$ can be defined by the formula

$$\Psi^{-1}_{c, d}(f: c \to R(d)) = (L(c) \stackrel{L(f)}{\to} L(R(d)) \stackrel{\varepsilon_d}{\to} d)$$

where $\varepsilon_d \coloneqq \Psi^{-1}_{R(d), d}(1_{R(d)})$. This is by appeal to the proof of the Yoneda lemma applied to the transformation

$$\Psi^{-1}_{-, d}: \hom_C(-, R(d)) \to \hom_D(L(-), d)$$

For the naturality of $\Psi^{-1}$ in the argument $(-)$ would imply that given $f: c \to R(d)$, we have a commutative square

$$\array{ \hom_C(R(d), R(d)) & \stackrel{\Psi^{-1}_{R(d), d}}{\to} & \hom_D(L(R(d)), d) \\ \hom_C(f, R(d)) \big\downarrow & & \big\downarrow \hom_D(L(f), d) \\ \hom_C(c, R(d)) & \underset{\Psi^{-1}_{c, d}}{\to} & \hom_D(L(c), d) }$$

Chasing the element $1_{R(d)}$ down and then across, we get $f: c \to R(d)$ and then $\Psi^{-1}_{c, d}(f)$. Chasing across and then down, we get $\varepsilon_d$ and then $\varepsilon_d \circ L(f)$. This completes the verification of the claim.

Corollary

An adjunction in its core 2-groupoid $Core(Cat)$ is an adjoint equivalence.

Enriched adjoint functors

Similarly one sees:

Example

For $V$ a cosmos for enrichment, an adjunction in the 2-category VCat of $V$-enriched categories is equivalently a pair $V$-enriched functors.

Example

Let $U \,\colon\, Grp \to Set$ from Grp to Set denote the usual forgetful functor from Grp to Set. When we say “$F(X)$ is the free group generated by a set $X$”, we mean there is a function $\eta_X \,\colon\, X \to U(F(X))$ which is universal among functions from $X$ to the underlying set of a group, which means in turn that given a function $f: X \to U(G)$, there is a unique group homomorphism $g \colon F(X) \to G$ such that

$$f = (X \stackrel{\eta_X}{\to} U(F(X)) \stackrel{U(g)}{\to} U(G))$$

Here $\eta_X$ is a component of what we call the unit of the adjunction $F \dashv U$, and the equation above is a recipe for the relationship between the map $g: F(X) \to G$ and the map $f: X \to U(G)$ in terms of the unit.

Adjoint $(\infty,1)$-functors

Proposition

An adjunction in the homotopy 2-category of $(\infty,1)$-categories is equivalently a pair of adjoint $(\infty,1)$-functors.

(Riehl & Verity 2015, Rem. 4.4.5; Riehl & Verity 2022, Prop. F.5.6; see there for more).

Remark

In view of Prop. , the remarkable aspect of Prop. is that the homotopy 2-category of $\infty$-categories is sufficient to detect adjointness of $\infty$-functors, which would, a priori, be defined as a kind of higher homotopy-coherent adjointness in the full $(\infty,2)$-category $Cat_{(\infty,1)}$. For more on this reduction of homotopy-coherent adjunctions to plain adjunctions see Riehl & Verity 2016, Thm. 4.3.11, 4.4.11.

Related concepts

• adjoint functor, adjoint (∞,1)-functor

• left adjoint, right adjoint

• duality

• adjunct

• dual adjunction, Galois connection

• monoidal adjunction

• enriched adjunction

• derived adjunction

• adjoint monad

• heteromorphism

• adjoint string

  • adjoint triple, adjoint quadruple

• ambidextrous adjunction

• adjoint cylinder

• adjoint logic

References

Adjunctions in 2-categories were introduced (together with the notion of strict 2-categories itself) in:

• Jean-Marie Maranda, pp. 762 in: Formal categories, Canadian Journal of Mathematics 17 (1965) 758-801 [doi:10.4153/CJM-1965-076-0, pdf]

Though see also the following, which uses more modern terminology:

• Max Kelly, §2 in: Adjunction for enriched categories, in: Reports of the Midwest Category Seminar III, Lecture Notes in Mathematics 106, Springer (1969) [doi:10.1007/BFb0059145]

A thorough 2-categorical account is contained in:

• Claude Auderset: Adjonctions et monades au niveau des $2$-catégories, Cahiers de topologie et géométrie différentielle 15 1 (1974) 3-20.

• Stephen Schanuel, Ross Street: The free adjunction, Cahiers de topologie et géométrie différentielle catégoriques 27 1 (1986) 81-8

Review:

• Saunders MacLane, §XII.4 of: Categories for the Working Mathematician, Graduate Texts in Mathematics 5 Springer (second ed. 1997) [doi:10.1007/978-1-4757-4721-8]

• Steve Lack, §2.1 in: A 2-categories companion, in: Towards Higher Categories, The IMA Volumes in Mathematics and its Applications 152 Springer (2010) [arXiv:math.CT/0702535, doi:10.1007/978-1-4419-1524-5_4]

• Niles Johnson, Donald Yau, Chapter 6 of: 2-Dimensional Categories, Oxford University Press 2021 (arXiv:2002.06055, doi:10.1093/oso/9780198871378.001.0001)

Fr the special case of adjoint functors see any text on category theory (and see the references at adjoint functor), for instance:

• Francis Borceux, Vol 1, Section 3 of Handbook of Categorical Algebra

• geometry of physics – categories and toposes – Adjunctions

For some early history and illustrative examples see

• Joachim Lambek, The Influence of Heraclitus on Modern Mathematics, In Scientific Philosophy Today: Essays in Honor of Mario Bunge, edited by Joseph Agassi and Robert S Cohen, 111–21. Boston: D. Reidel Publishing Co. (1982) (doi:10.1007/978-94-009-8462-2_6)

  (more along these lines at objective logic).

The fundamental role of adjoint functors in logic/type theory originates with the observaiton that substitution forms an adjoint triple with existential quantification and universal quantification:

• William Lawvere, Adjointness in Foundations, (tac:16), Dialectica 23 (1969), 281-296

• William Lawvere, Quantifiers and sheaves, Actes, Congrès intern, math., 1970. Tome 1, p. 329 à 334 (pdf)

Adjunctions in programming languages (though mainly again just adjoint functors):

• Ralf Hinze, Generic Programming with Adjunctions, In: J. Gibbons (ed.) Generic and Indexed Programming Lecture Notes in Computer Science, vol 7470. Springer 2012 (pdf, slides doi:10.1007/978-3-642-32202-0_2)

• Jeremy Gibbons, Fritz Henglein, Ralf Hinze, Nicolas Wu, Relational Algebra by Way of Adjunctions, Proceedings of the ACM on Programming Languages archive Volume 2 Issue ICFP, September 2018 Article No. 86 (pdf, doi:10.1145/3236781)

See also

• Wikipedia, Adjoint Functors

• Catsters, Adjunctions (YouTube)

---