nLab geometry of physics -- categories and toposes
This entry is one chapter of geometry of physics,
prepared for lectures given at:
Modern Mathematics Methods in Physics, Diffeology, Categories and Toposes and Non-commutative Geometry Summer School, Nesin Mathematics Village — Şirince, Turkey (2018)
download this entry: pdf (418 pages)
next chapters: smooth sets, supergeometry
Context
Category theory
Concepts
Universal constructions
Theorems
Extensions
Applications
Topos Theory
Background
Toposes
Internal Logic
Topos morphisms
Extra stuff, structure, properties
Cohomology and homotopy
In higher category theory
Theorems
Category theory and topos theory concern the general abstract structure underlying algebra, geometry and logic. They are ubiquituous in and indispensible for organizing conceptual mathematical frameworks.
We give here an introduction to the basic concepts and results, aimed at providing background for the synthetic higher supergeometry of relevance in formulations of fundamental physics, such as used in the chapters on perturbative quantum field theory and on fundamental super p-branes. For quick informal survey see Introduction to Higher Supergeometry.
This makes use of the following curious dictionary between category theory/topos theory and the geometry of generalized spaces, which we will explain in detail (following Grothendieck 65, Lawvere 86, p. 17, Lawvere 91):
The perspective is that of functorial geometry (Grothendieck 65). (For more exposition of this point see also at motivation for sheaves, cohomology and higher stacks.) This dictionary implies a wealth of useful tools for handling and reasoning about geometry:
We discuss below that sheaf toposes, regarded as categories of generalized spaces via the above disctionary, are “convenient contexts” for geometry (Prop. below), in the technical sense that they provide just the right kind of generalization that makes all desireable constructions on spaces actually exist:
| sheaf topos | as category of generalized spaces |
|---|---|
| Yoneda embedding: | contains and generalizes ordinary spaces |
| has all limits: | contains all Cartesian products and intersections |
| has all colimits: | contains all disjoint unions and quotients |
| cartesian closure: | contains all mapping spaces |
| local cartesian closure: | contains all fiber-wise mapping spaces |
Notably mapping spaces play a pivotal role in physics, in the guise of spaces of field histories, but fall outside the applicability of traditional formulations of geometry based on just manifolds. Topos theory provides their existence (Prop. below) and the relevant infrastructure, for example for the construction of transgression of differential forms to mapping spaces of smooth sets, that is the basis for sigma-model-field theories. This is discussed in the following chapters on smooth sets and on supergeometry.
In conclusion, one motivation for category theory and topos theory is a posteriori: As a matter of experience, there is just no other toolbox that allows to deeply understand and handle the geometry of physics. Similar comments apply to a wealth of other topics of mathematics.
But we may offer also an a priori motivation:
Category theory is the theory of duality.

Duality is of course an ancient notion in philosophy. At least as a term, it makes a curious re-appearance in the conjectural theory of fundamental physics formerly known as string theory, in the guise of duality in string theory. In both cases, the literature left some room in delineating what precisely is meant. But the philosophically inclined mathematician could notice (see Lambek 82) that an excellent candidate to make precise the idea of duality is the mathematical concept of adjunction, from category theory. This is particularly pronounced for adjoint triples (Remark below) and their induced adjoint modalities (Lawvere 91, see Def. below), which exhibit a given “mode of being” of any object as intermediate between two dual opposite extremes (Prop. below):
For example, cohesive geometric structure on generalized spaces is captured, this way, as modality in between the discrete and the codiscrete (Example , and Def. below).
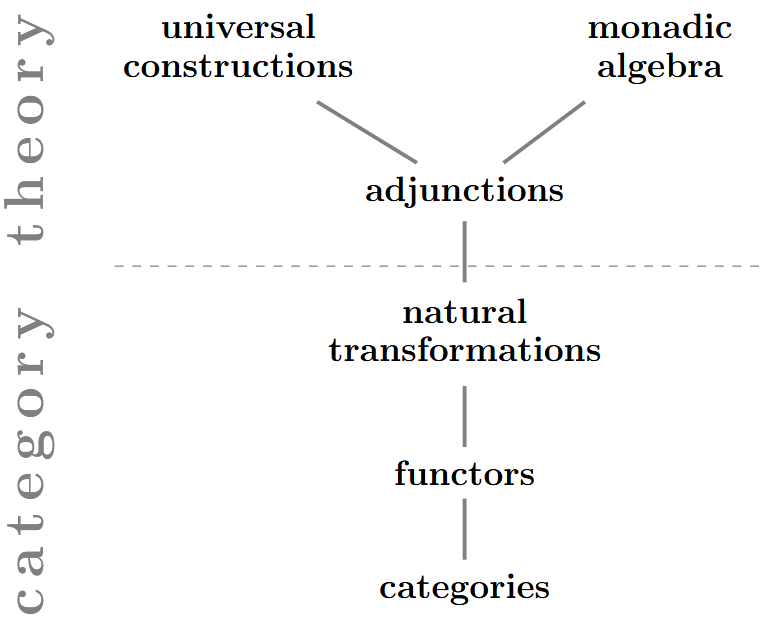
Historically, category theory was introduced in order to make precise the concept of natural transformation: The concept of functors was introduced just so as to support that of natural transformations, and the concept of categories only served that of functors (see Freyd 1964,, p 1).
But natural transformations are, in turn, exactly the basis for the concept of adjoint functors (Def. below), equivalently adjunctions between categories (Prop. below).
Shown below is the “Yin-Yang identity” (the triangle identity, cf. Prop. below) characterizing adjunctions.
All universal constructions — the heart of category theory — are special cases of adjoint functors, hence of dualities, if we follow Lambek 82: This includes the concepts of limits and colimits (Def. below), ends and coends (Def. below) Kan extensions (Prop. below), and the behaviour of these constructions, such as for instance the free co-completion nature of the Yoneda embedding (Prop. below).
Therefore it makes sense to regard category theory as the theory of adjunctions,
hence the theory of duality:
| hierarchy of concepts | category theory | enriched | homotopical |
|---|---|---|---|
| adjunction of adjunctions duality of dualities | Def. | Def. | |
| adjoint equivalence dual equivalence | Def. | Def. | Def. |
| adjunction duality | Def. | Def. | Def. |
| natural transformation | Def. | Def. | |
| functor | Def. | Def. | |
| category | Def. | Def. | Def. |
The pivotal role of adjunctions in category theory (Lawvere 08) and in the foundations of mathematics (Lawvere 69, Lawvere 94 ) was particularly amplified by F. W. Lawvere1. Moreover, Lawvere saw the future of category theory (Lawvere 91) as concerned with adjunctions expressing systems of archetypical dualities that reveal foundations for geometry (Lawvere 07) and physics (Lawvere 97, see Def. and Def. below). He suggested (Lawvere 94) this as a precise formulation of core aspects of the theory of everything of early 19th century philosophy: Hegel‘s Science of Logic.
These days, of course, theories of everything, such as string theory, are understood less ambitiously than Hegel’s ontological process, as mathematical formulations of fundamental theories of physics, that could conceptually unify the hodge-podge of currently available “standard models” of particle physics and of cosmology to a more coherent whole.
The idea of duality in string theory refers to different perspectives on physics that appear dual to each other while being equivalent. But one of the basic results of category theory (Prop. , below) is that equivalence is indeed a special case of adjunction. This allows to explore the possibility that there is more than a coincidence of terms.
Of course the usage of the term duality in string theory is too loose for one to expect to be able to refine each occurrence of the term in the literature to a mathematical adjunction. However, we will see mathematical formalizations of core aspects of key string-theoretic dualities, such as topological T-duality and the duality between M-theory and type IIA string theory, in terms of adjunctions. Indeed, at the heart of these dualities in string theory is the phenomenon of double dimensional reduction, which turns out to be formalized by one of the most fundamental adjunctions in (higher) category theory: base change along the point inclusion into a classifying space. All this is discussed in the chapter on fundamental super p-branes.
This suggests that there may be a deeper relation here between the superficially alien uses of the word “duality”, that is worth exploring.
In this respect it is worth noticing that core structure of string/M-theory arises via universal constructions from the superpoint (as explained in the chapter on fundamental super p-branes), while the superpoint itself arises, in a sense made precise by category theory, “from nothing”, by a system of twelve adjunctions (explained in the chapter on supergeometry).
Here we introduce the requisites for understanding these statements.
Contents
- Basic notions of Category theory
- Basic notions of Categorical algebra
- Universal constructions
- Basic notions of Topos theory
- Gros toposes
- Basic notions of homotopy theory
- Factorization systems
- Homotopy
- The homotopy category
- Derived functors
- Quillen adjunctions
- Mapping cones
- Categories of fibrant objects
- Homotopy fibers
- Homotopy pullbacks
- Long fiber sequences
- -Groupoids I): Topological homotopy theory
- Universal constructions
- Homotopy
- Cell complexes
- Fibrations
- The classical model structure on topological spaces
- The classical homotopy category
- Model structure on pointed spaces
- Model structure on compactly generated spaces
- Topological enrichment
- Model structure on topological functors
- -Groupoids II): Simplicial homotopy theory
- Simplicial sets
- Simplicial homotopy
- Kan complexes
- Geometric realization
- The classical model structure on simplicial sets
- Basic notions of higher topos theory
- Gros -Toposes
Basic notions of Category theory
We introduce here the basic notions of category theory, along with examples and motivation from geometry:
This constitutes what is sometimes called the language of categories. While we state and prove some basic facts here, notably the notorious Yoneda lemma (Prop. below), what makes category theory be a mathematical theory in the sense of a coherent collection of non-trivial theorems is all concerned with the topic of universal constructions, which may be formulated (only) in this language. This we turn to further below.
Categories and Functors
The notion of a category (Def. below) embodies the idea of structuralism applied to concepts in mathematics: it collects, on top of the set (or generally: class) of mathematical objects that belong to it, also all the structure-preserving maps between them, hence the homomorphisms in the case of Bourbaki-style mathematical structures.
The first achievement of the notion of a category is to abstract away from such manifestly concrete categories (Examples , below) to more indirectly defined mathematical objects whose “structure” is only defined, after the fact, by which maps, now just called morphisms, there are between them.
This structuralism-principle bootstraps itself to life by considering morphisms between categories themselves to be those “maps” that respect their structuralism, namely the connectivity and composition of the morphisms between their objects: These are the functors (Def. below).
For the purpose of geometry, a key class of examples of functors are the assignments of algebras of functions to spaces, this is Example below.
Definition
(category)
A category is
-
for each pair of objects, a set , called the set of morphisms from to , or the hom-set, for short.
We denote the elements of this set by arrows like this:
-
for each object a morphism
called the identity morphism on ;
-
for each triple of objects, a function
called composition;
such that:
-
for all pairs of objects unitality holds: given
then
-
for all quadruples of objects composition satifies associativity: given
then
The archetypical example of a category is the category of sets:
Example
The class of all sets with functions between them is a category (Def. ), to be denoted Set:
-
;
-
;
-
identity function on set ;
-
.
More generally all kind of sets with structure, in the sense going back to Bourbaki, form categories, where the morphisms are the homomorphisms (whence the name “morphism”!). These are called concrete categories (we characterize them precisely in Example , further below):
Example
(basic examples of concrete categories)
For a kind of mathematical structure, there is the category (Def. ) whose objects are the corresponding structured sets, and whose morphisms are the corresponding structure homomorphisms, hence the functions of underlying sets which respect the given structure.
Basic examples of concrete categories include the following:
This is the motivation for the terminology “categories”, as the examples in Example are literally categories of mathematical structures. But not all categories are “concrete” in this way.
Some terminology:
Definition
Let be a category (Def. ), then a directed graph with edges labeled by morphisms of the category is called a commuting diagram if for any two vertices any two ways of passing along edges from one to the other yields the same composition of the corresponding morphisms.
For example, a commuting triangle is
while a commuting square is
Definition
If a category (Def. ) happens to have as class of objects an actual set (i.e. a small set instead of a proper class), then is called a small category.
As usual, there are some trivial examples, that are however usefully made explicit for the development of the theory:
Example
(initial category and terminal category)
-
The terminal category is the category (Def. ) whose class of objects is the singleton set, and which has a single morphism on this object, necessarily the identity morphism.
-
The initial category or empty category is the category (Def. ) whose class of objects is the empty set, and which, hence, has no morphism whatsoever.
Clearly, these are small categories (Def. ).
Example
(preordered sets as thin categories)
Let be a preordered set. Then this induces a small category whose set of objects is , and which has precisely one morphism whenever , and no such morphism otherwise:
Conversely, every small category with at most one morphism from any object to any other, called a thin category, induces on its set of objects the structure of a partially ordered set via (1).
Here the axioms for preordered sets and for categories match as follows:
| reflexivity | transitivity | |
|---|---|---|
| partially ordered sets | ||
| thin categories | identity morphisms | composition |
Definition
For a category (Def. ), a morphism
is called an isomorphism if there exists an inverse morphism
namely a morphism such that the compositions with are equal to the identity morphisms on and , respectively
Definition
(groupoid)
If is a category in which every morphism is an isomorphism (Def. ), then is called a groupoid.
Example
For a group, there is a groupoid (Def. ) with a single object, whose single hom-set is , with identity morphism the neutral element and composition the group operation in :
In fact every groupoid with precisely one object is of the form.
Remark
(groupoids and homotopy theory)
Even though groupoids (Def. ) are special cases of categories (Def. ), the theory of groupoids in itself has a rather different flavour than that of category theory: Part of the homotopy hypothesis-theorem is that the theory of groupoids is really homotopy theory for the special case of homotopy 1-types.
(In applications in homotopy theory, groupoids are considered mostly in the case that the class of objects is in fact a set: small groupoids, Def. ).
For this reason we will not have more to say about groupoids here, and instead relegate their discussion to the section on homotopy theory, further below.
There is a range of constructions that provide new categories from given ones:
Example
(opposite category and formal duality)
Let be a category. Then its opposite category has the same objects as , but the direction of the morphisms is reversed. Accordingly, composition in the opposite category is that in , but with the order of the arguments reversed:
-
;
-
.
Hence for every statementa about some category there is a corresponding “dual” statement about its opposite category, which is “the same but with the direction of all morphisms reversed”. This relation is known as formal duality.
Example
Let and be two categories (Def. ). Then their product category has as objects pairs with and , and as morphisms pairs , , and composition is defined by composition in each entry:
-
;
Definition
(functor)
Let and be two categories (Def. ). A functor from to , to be denoted
is
such that
-
For each object the identity morphism is respected:
-
for each triple of objects, composition is respected: given
we have
Example
(categories of small categories and of small groupoids)
It is clear that functors (Def. ) have a composition operation given componentwise by the composition of their component functions. Accordingly, this composition is unital and associative. This means that there is
Example
Let be a category (Def. ). Then its hom-functor
is the functor (Def. ) out of the product category (Def. ) of with its opposite category to the category of sets, which sends a pair of objects to the hom-set between them, and which sends a pair of morphisms, with one of them into and the other out of , to the operation of composition with these morphisms:
Definition
(monomorphism and epimorphism)
Let be a category (Def. ). Then a morphism in is called
-
a monomorphism if for every object the hom-functor (Example ) out of takes to an injective function of hom-sets:
-
an epimorphism if for every object the hom-functor (Example ) into takes to an injective function:
Definition
(full, faithful and fully faithful functors)
A functor (Def. ) is called
-
a full functor if all its hom-functions are surjective functions
-
a faithful functor if all its hom-functions are injective functions
-
a fully faithful functor if all its hom-functions are bijective functions
A fully faithful functor is also called a full subcategory-inclusion. We will denote this situation by
Example
(full subcategory on a sub-class of objects)
Let be a category (Def. ) and let be a sub-class of its class of objects. The there is a category whose class of objects is , and whose morphisms are precisely the morphisms of , between these given objects:
with identity morphisms and composition defined as in . Then there is a fully faithful functor (Def. )
which is the evident inclsuion on objects, and the identity function on all hom-sets.
This is called the full subcategory of on the objects in .
Beware that not every fully faithful functor is, in components, exactly of this form, but, assuming the axiom of choice, every fully faithful functor is so up to equivalence of categories (Def. ).
The concept of faithful functor from Def. allows to make precise the idea of concrete category from Example :
Example
(structured sets and faithful functors)
Let be a kind of mathematical structure and let be the category of -structured sets. Then there is the forgetful functor
which sends each structured set to the underlying set (“forgetting” the structure that it carries), and which sends functions of sets to themselves. That a homomorphism of structured sets is a function between the underlying sets satisfying a special condition implies that this is a faithful functor (Def. ).
Conversely, it makes sense to define structured sets in general to be the objects of a category which is equipped with a faithful functor to the category of sets. See at structure for more on this.
Example
(spaces seen via their algebras of functions)
In any given context of geometry, there is typically a functor which sends any space of the given kind to its algebra of functions, and which sends a map (i.e. homomorphism) between the given spaces to the algebra homomorphism given by precomposition with that map (a hom-functor, Def. ). Schematically:
Since the precomposition operation reverses the direction of morphisms, as shown, these are functors from the given category of spaces to the opposite (Example ) of the relevant category of algebras.
In broad generality, there is a duality (“Isbell duality”) between geometry/spaces and algebra/algebras of functions) (“space and quantity”, Lawvere 86).
We now mention some concrete examples of this general pattern:
topological spaces and C*-algebras
Consider
-
the category Top of compact topological Hausdorff spaces with continuous functions between them;
-
the category C*Alg of unital C*-algebras over the complex numbers
Then there is a functor (Def. )
from the former to the opposite category of the latter (Example ) which sends any compact topological space to its C*-algebra of continuous functions with values in the complex numbers, and which sends every continuous function between compact spaces to the C*-algebra-homomorphism that is given by precomposition:
Part of the statement of Gelfand duality is that this is a fully faithful functor, hence exhibiting a full subcategory-inclusion (Def. ), namely that of commutative C*-algebras:
affine schemes and commutative algebras
The starting point of algebraic geometry is to consider affine schemes as the formal duals (Example ) of finitely generated commutative algebras over some algebraically closed ground field :
Beware that the immediate identification (2) is often obscured by the definition of affine schemes as locally ringed spaces. While the latter is much more complicated, at face value, in the end it yields an equivalent category (Def. below) to the simple formal dualization (Example ) in (2), see here. Already in 1973 Alexander Grothendieck had urged to abandon, as a foundational concept, the more complicated definition in favor of the simpler one in (2), see Lawvere 03.
smooth manifolds and real associative algebras
Consider
-
the category SmthMfd of smooth manifolds with smooth functions between them;
-
the category Alg of associative algebras over the real numbers
Then there is a functor (Def. )
from the former to the opposite category of the latter (Def. ), which sends any smooth manifold to its associative algebra of continuous functions to the real numbers, and which sends every smooth function between smooth manifolds to the algebra homomorphism that is given by precomposition:
The statement of Milnor's exercise is that this this is a fully faithful functor, hence exhibiting a full subcategory-inclusion (Def. ):
These two statements, expressing categories of spaces as full subcategories of opposite categories of categories of algebras, are the starting point for many developments in geometry, such as algebraic geometry, supergeometry, noncommutative geometry and noncommutative topology.
Since a fully faithful functor/full subcategory-embedding exhibits the objects of as a consistent generalization of the objects of , one may turn these examples around and define more general kinds of spaces as formal duals (Example ) to certain algebras:
infinitesimally thickened points and formal Cartesian spaces
The category of infinitesimally thickened points is, by definition, the full subcategory (Example ) of the opposite category (Example ) of that of commutative algebras (Example ) over the real numbers
on those with a unique maximal ideal which is a finite-dimensional as an -vector space and a nilradical: for each there exists such that .
The category of formal Cartesian spaces is, by definition, the full subcategory (Example ) of the opposite category (Example ) of that of commutative algebras (Example ) over the real numbers
on those which are tensor products of algebras, of an algebra of smooth functions on a Cartesian space , for some , and the algebra of functions on an infinitesimally thickened point.
Notice that the formal Cartesian spaces are fully defined by this assignment.
super points and super Cartesian spaces
The category of super points is by definition, the full subcategory (Example ) of the opposite category (Example ) of that of supercommutative algebras (Example ) over the real numbers
on the Grassmann algebras:
More generally, the category of super Cartesian spaces is by definition, the full subcategory
on the tensor product of algebras, over of the algebra of smooth functions on a Cartesian space, and a Grassmann algebra, as above.
Notice that the super Cartesian spaces are fully defined by this assignment. We discuss this in more detail in the chapter on supergeometry.
Natural transformations and presheaves
Given a system of (homo-)morphisms (“transformations”) in some category (Def. )
between objects that depend on some variable , hence that are values of functors of (Def. ), one says that this is natural, hence a natural transformation (Def. below) if it is compatible with (homo-)morphisms of the variable itself.
These natural transformations are the evident homomorphisms between functors
and hence there is a category of functors between any two categories (Example below).
A key class of such functor categories are those between an opposite category and the base category of sets, these are also called categories of presheaves (Example below). It makes good sense (Remark below) to think of these as categories of “generalized objects of ”, a perspective which is made precise by the statement of the Yoneda lemma (Prop. below) and the resulting Yoneda embedding (Prop. below). This innocent-looking lemma is the heart that makes category theory tick.
Definition
(natural transformation and natural isomorphism)
Given two categories and (Def. ) and given two functors and from to (Def. ), then a natural transformation from to
is
such that
-
for each morphism we have a commuting square (Def. ) of the form
(4)(sometimes called the naturality square of the natural transformation).
If all the component morphisms are isomorphisms (Def. ), then the natural transformation is called a natural isomorphism.
For
two natural transformations as shown, their composition is the natural transformation
whose components (3) are the compositions of the components of and :
Example
(reduction of formal Cartesian spaces)
On the category FormalCartSp of formal Cartesian spaces Example , consider the endofunctor
which sends each formal Cartesian space to the underlying ordinary Cartesian space, forgetting the infinitesimally thickened point-factor. Moreover, on morphisms this functor is defined via the retraction
as
This is indeed functorial due to the fact that any algebra homomorphism needs to send nilpotent elements to nilpotent elements, so that the following identity holds:
Then there is a natural transformation (Def. ) from this functor to the identity functor
whose components inject the underlying Cartesian space along the unit point inclusion of the infinitesimally thickened point:
The commutativity of this naturality square is again the identity (6).
Example
Let and be categories (Def. ). Then the category of functors between them, to be denoted , is the category whose objects are the functors (Def. ) and whose morphisms are the natural transformations between functors (Def. ) and whose composition operation is the composition of natural transformations (5).
Example
Given a category (Def. ), a functor (Def. ) of the form
hence out of the opposite category of (Def. ), into the category of sets (Example ) is also called a presheaf (for reasons discussed below) on or over .
The corresponding functor category (Example )
is hence called the category of presheaves over .
Example
Given a category (Def. ), the hom-functor (Example ) induces the following functor (Def. ) from to its category of presheaves (Def. ):
The presheaves in the image of this functor are called the representable presheaves and is called their representing object.
The functor (7) is also called the Yoneda embedding, due to Prop. below.
Remark
(presheaves as generalized spaces)
If a given category (Def. ) is thought of as a category of spaces of sorts, as those in Example , then it will be most useful to think of the corresponding category of presheaves (Def. ) as a category of generalized spaces probe-able by the test spaces in (Lawvere 86, p. 17).
Namely, imagine a generalized space which is at least probe-able by spaces in . This should mean that for each object there is some set of geometric maps “”. Here the quotation marks are to warn us that, at this point, is not defined yet; and even if it were, it is not expected to be an object of , so that, at this point, an actual morphism from to is not definable. But we may anyway consider some abstract set
whose elements we do want to think of maps (homomorphisms of spaces) from to .
That this is indeed consistent, in that we may actually remove the quotation remarks on the right of (8), is the statement of the Yoneda lemma, which we discuss as Prop. below.
A minimum consistency condition for this to make sense (we will consider further conditions later on when we discuss sheaves) is that we may consistently pre-compose the would-be maps from to with actual morphisms in . This means that for every such morphism there should be a function between these sets of would-be maps
which respects composition and identity morphisms. But in summary, this says that what we have defined thereby is actually a presheaf on (Def. ), namely a functor
For consistency of regarding this presheaf as a presheaf of sets of plots of a generalized space, it ought to be true that every “ordinary space”, hence every object , is also an example of a “generalized space probe-able by” object of , since, after all, these are the spaces which may manifestly be probed by objects , in that morphisms are already defined.
Hence the incarnation of as a generalized space probe-able by objects of should be the presheaf , hence the presheaf represented by (Example ), via the Yoneda functor (7).
At this point, however, a serious consistency condition arises: The “ordinary spaces” now exist as objects of two different categories: on the one hand there is the original , on the other hand there is its Yoneda image in the category of generalized spaces. Hence we need to know that these two perspectives are compatible, notably that maps between ordinary spaces are the same whether viewed in or in the more general context of .
That this, too, holds true, is the statement of the Yoneda embedding, which we discuss as Prop. below.
Eventually one will want to impose one more consistency condition, namely that plots are determined by their local behaviour. This is the sheaf condition (Def. below) and is what leads over from category theory to topos theory below.
Proposition
Let be a category (Def. ), any object, and a presheaf over (Def. ).
Then there is a bijection
between the hom-set of the category of presheaves from the presheaf represented by (7) to , and the set which is assigned by to .
Proof
By Example , an element in the set on the left is a natural transformation (Def. ) of the form
hence given by component functions (3)
for each . In particular there is the component at
and the identity morphism on is a canonical element in the set on the left. The statement to be proven is hence equivalently that for every element in there is precisely one such that this element equals .
Now the condition to be satisfied by is that it makes its naturality squares (4) commute (Def. ). This includes those of the form
for any morphism
As the diagram chase of elements on the right shows, this commutativity (Def. ) fixes for all and all uniquely in terms of the element .
It remains only to see that there is no condition on the element , hence that with defined this way, the commutativity of all the remaining naturality squares is implies: The general naturality square for a morphism is of the form
As shown on the right, the commutativity of this diagram now follows from the functoriality of the presheaf .
As a direct corollary, we obtain the statement of the Yoneda embedding:
Proposition
The assignment (7) of represented presheaves (Example ) is a fully faithful functor (Def. ), hence exhibits a full subcategory inclusion
of the given category into its category of presheaves.
Proof
We need to show that for all the function
is a bijection. But the Yoneda lemma (Prop. ) states a bijection the other way around
and hence it is sufficient to see that this is a left inverse to (9). This follows by inspection, as shown in the third line above.
As a direct corollary we obtain the following alternative characterization of isomorphisms, to be compared with the definition of epimorphisms/monomorphisms in Def. :
Example
(isomorphism via bijection of hom-sets)
Let be a category (Def. ), let be a pair of objects, and let be a morphism between them. Then the following are equivalent:
-
is an isomorphism (Def. ),
-
the hom-functors into and out of take values in bijections of hom-sets: i.e. for all objects , we have
and
Adjunctions
The concepts of categories, functors and natural transformations constitute the “language of categories”. This language now allows to formulate the concept of adjoint functors (Def. ) and more generally that of adjunctions (Def. below. This is concept that category theory, as a theory, is all about.
Part of the data involved in an adjunction is its adjunction unit and adjunction counit (Def. below) and depending on their behaviour special cases of adjunctions are identified (Prop. below), which we discuss in detail in following sections:
| adjunction Def. , Def. | unit is iso: | |
| coreflection Def. | ||
| counit is iso: | reflection Def. | adjoint equivalence Def. |
We now discuss four equivalent definitions of adjoint functors:
-
via adjunction unit and -counit satisfying triangle identities (Prop. );
-
via representing objects (Prop. );
-
via universal morphisms (Prop. below).
Then we discuss some key properties:
Definition
Let and be two categories (Def. ), and let
be a pair of functors between them (Def. ), as shown. Then this is called a pair of adjoint functors (or an adjoint pair of functors) with left adjoint and right adjoint, denoted
if there exists a natural isomorphism (Def. ) between the hom-functors (Example ) of the following form:
This means that for all objects and there is a bijection of hom-sets
which is natural in and . This isomorphism is called the adjunction hom-isomorphism and the image of a morphism under this bijections is called the adjunct of . Conversely, is called the adjunct of .
Naturality here means that for every pair of morphisms in and in , the resulting square
commutes (Def. ), where the vertical morphisms are given by the hom-functor (Example ).
Explicitly, this commutativity, in turn, means that for every morphism with adjunct , the adjunct of the composition is
Definition
(adjunction unit and counit)
Given a pair of adjoint functors
according to Def. , one says that
-
for any the adjunct of the identity morphism on is the unit morphism of the adjunction at that object, denoted
-
for any the adjunct of the identity morphism on is the counit morphism of the adjunction at that object, denoted
Remark
It happens that there are sequences of adjoint functors:
If two functors are adjoint to each other as in Def. , we also say that we have an adjoint pair:
It may happen that one functor participates on the right and on the left of two such adjoint pairs and (not the same “” and “” as before!) in which case one may speak of an adjoint triple:
Below in Example we identify adjoint triples as adjunctions of adjunctions.
Similarly there are adjoint quadruples, etc.
Notice that in the case of an adjoint triple (12), the adjunction unit of and the adjunction counit of (Def. ) provide, for each object in the domain of , a diagram
which is usefully thought of as exhibiting the nature of as being in between two opposite extreme aspects and of . This is illustrated by the following examples, and formalized by the concept of modalities that we turn to in Def. below.
Example
(floor and ceiling as adjoint functors)
Consider the canonical inclusion
of the integers into the real numbers, both regarded as preorders in the standard way (“lower or equal”). Regarded as full subcategory-inclusion (Def. ) of the corresponding thin categories, via Example , this inclusion functor has both a left and right adjoint functor (Def. ):
-
the left adjoint to is the ceiling function;
-
the right adjoint to is the floor function;
forming an adjoint triple (Def. )
The adjunction unit and adjunction counit express that each real number is in between its “opposite extreme integer aspects” (13) given by floor and ceiling
Proof
First of all, observe that we indeed have functors (Def. )
since floor and ceiling preserve the ordering relation.
Now in view of the identification of preorders with thin categories in Example , the hom-isomorphism (10) defining adjoint functors of the form says for all and , that we have
This is clearly already the defining condition on the floor function .
Similarly, the hom-isomorphism defining adjoint functors of the form says that for all and , we have
This is evidently already the defining condition on the floor function .
Notice that in both cases the condition of a natural isomorphism in both variables, as required for an adjunction, is automatically satisfied: For let and , then naturality as in (11) means, again in view of the identifications in Example , that
Here the logical implications are equivalently functions between sets that are either empty or singletons. But Functions between such sets are unique, when they exist.
Example
(discrete and codiscrete topological spaces)
Consider the “forgetful functor” from the category Top of topological spaces (Example ) to the category of sets (Def. ) which sends every topological space to its underlying set.
This has
-
a left adjoint (Def. ) which equips a set with its discrete topology,
-
a right adjoint which equips a set with the codiscrete topology.
These hence form an adjoint triple (Remark )
Hence the adjunction counit of and the adjunction unit of exhibit every topology on a given set as “in between the opposite extremes” (13) of the discrete and the co-discrete
Lemma
(pre/post-composition with (co-)unit followed by adjunct is adjoint functor)
If a functor is the right adjoint
in a pair of adjoint functors (Def. ), then its application to any morphism is equal to the joint operation of pre-composition with the -adjunction counit (Def. ), followed by passing to the -adjunct:
Dually, if is a left adjoint
then its action on any morphism equals the joint operation of post-composition with the -adjunction unit (Def. ), followed by passing to the -adjunct:
In particular, if is the middle functor in an adjoint triple (Remark )
then these two operations coincide:
Proof
For the first equality, consider the following naturality square (4) for the adjunction hom-isomorphism (10):
Chasing the identity morphism through this diagram yields the claimed equality, as shown on the right. Here we use that the left adjunct? of the identity morphism is the adjunction counit, as shown.
The second equality is fomally dual:
We now turn to a sequence of equivalent reformulations of the condition of adjointness.
Proposition
(general adjuncts in terms of unit/counit)
Consider a pair of adjoint functors
according to Def. , with adjunction units and adjunction counits according to Def. .
Then
-
The adjunct of any morphism is obtained from and as the composite
(16)Conversely, the adjunct of any morphism is obtained from and as
(17) -
The adjunction units and adjunction counits are components of natural transformations of the form
and
-
The adjunction unit and adjunction counit satisfy the triangle identities, saying that
(18)and
Proof
For the first statement, consider the naturality square (11) in the form
and consider the element in the top left entry. Its image under going down and then right in the diagram is , by Def. . On the other hand, its image under going right and then down is , by Def. . Commutativity of the diagram means that these two morphisms agree, which is the statement to be shown, for the adjunct of .
The converse formula follows analogously.
The third statement follows directly from this by applying these formulas for the adjuncts twice and using that the result must be the original morphism:
For the second statement, we have to show that for every moprhism the following square commutes:
To see this, consider the naturality square (11) in the form
The image of the element in the top left along the right and down is , by Def. , while its image down and then to the right is , by the previous statement. Commutativity of the diagram means that these two morphisms agree, which is the statement to be shown.
The argument for the naturality of is directly analogous.
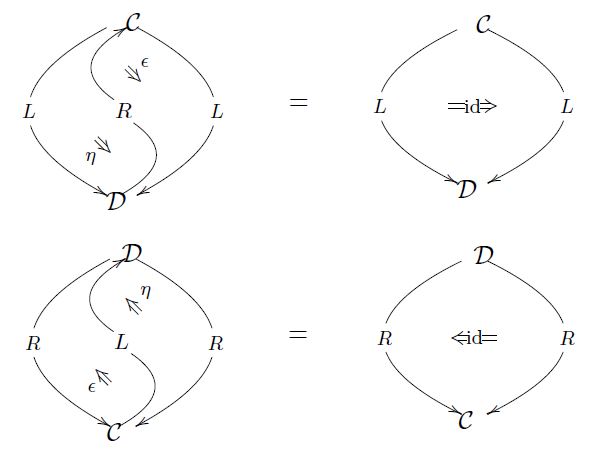
Proposition
(adjoint functors equivalent to adjunction in Cat)
Two functors
are an adjoint pair in the sense that there is a natural isomorphism (10) according to Def. , precisely if they participate in an adjunction in the 2-category Cat, meaning that

-
there exist natural transformations
and
-
which satisfy the triangle identities
and
Proof
That a hom-isomorphism (10) implies units/counits satisfying the triangle identities is the statement of the second two items of Prop. .
Hence it remains to show the converse. But the argument is along the same lines as the proof of Prop. : We now define forming of adjuncts by the formula (16). That the resulting assignment is an isomorphism follows from the computation
where, after expanding out the definition, we used naturality of and then the triangle identity.
Finally, that this construction satisfies the naturality condition (11) follows from the functoriality of the functors involved, and the naturality of the unit/counit:
The condition (10) on adjoint functors in Def. implies in particular that for every object the functor is a representable functor with representing object . The following Prop. observes that the existence of such representing objects for all is, in fact, already sufficient to imply that there is a right adjoint functor.
This equivalent perspective on adjoint functors makes manifest that adjoint functors are, if they exist, unique up to natural isomorphism, this is Prop. below.
Proposition
(adjoint functor from objectwise representing objects)
A functor has a right adjoint , according to Def. , already if for all objects there is an object such that there is a natural isomorphism
hence for each object a bijection
such that for each morphism , the following diagram commutes
(This is as in (11), except that only naturality in the first variable is required.)
In this case there is a unique way to extend from a function on objects to a function on morphisms such as to make it a functor which is right adjoint to . , and hence the statement is that with this, naturality in the second variable is already implied.
Proof
Notice that
-
in the language of presheaves (Example ) the assumption is that for each the presheaf
is represented (7) by the object , and naturally so.
-
In terms of the Yoneda embedding (Prop. )
we have
(20)
The condition (11) says equivalently that has to be such that for all morphisms the following diagram in the category of presheaves commutes
This manifestly has a unique solution
for every morphism under (20). But the Yoneda embedding is a fully faithful functor (Prop. ), which means that thereby also is uniquely fixed.
We consider one more equivalent characterization of adjunctions:
Definition
Let be two categories (Def. ) and let be a functor (Def. )
Then for an object, a universal morphism from to is
such that for any , any morphism factors through this unit as
for a unique morphism , to be called the adjunct of .
Proposition
(collection of universal morphisms equivalent to adjoint functor)
Let be a functor (Def. ). Then the following are equivalent:
-
has a left adjoint functor according to Def. .
-
For every object there is a universal morphism , according to Def. .
Proof
In one direction, assume a left adjoint is given. Define the would-be universal arrow at to be the unit of the adjunction via Def. . Then the statement that this really is a universal arrow is implied by Prop. .
In the other direction, assume that universal arrows are given. The uniqueness clause in Def. immediately implies bijections
Hence to satisfy (10) it remains to show that these are natural in both variables. In fact, by Prop. it is sufficient to show naturality in the variable . But this is immediate from the functoriality of applied in (21): For any morphism, we have
The following equivalent formulation (Prop. ) of universal morphisms is often useful:
Example
Let be a category, let be any object, and let be a functor.
-
The comma category is the category whose objects are pairs consisting of an object and morphisms in , and whose morphisms are the morphisms in that make a commuting triangle (Def. ):
There is a canonical functor
-
The comma category is the category whose objects are pairs consisting of an object and a morphism in , and whose morphisms are the morphisms in that make a commuting triangle (Def. ):
Again, there is a canonical functor
(22)
With this definition, the following is evident:
Proposition
(universal morphisms are initial objects in the comma category)
Let be a functor and an object. Then the following are equivalent:
-
is a universal morphism into (Def. );
-
is the initial object (Def. ) in the comma category (Example ).
After these equivalent characterizations of adjoint functors, we now consider some of their main properties:
Proposition
(adjoint functors are unique up to natural isomorphism)
The left adjoint or right adjoint to a functor (Def. ), if it exists, is unique up to natural isomorphism (Def. ).
Proof
Suppose the functor is given, and we are asking for uniqueness of its right adjoint, if it exists. The other case is directly analogous.
Suppose that are two functors which both are right adjoint to . Then for each the corresponding two hom-isomorphisms (10) combine to say that there is a natural isomorphism/
As in the proof of Prop. , the Yoneda lemma implies that
for some isomorphism
But then the uniqueness statement of Prop. implies that the collection of these isomorphisms for each object constitues a natural isomorphism between the functors (Def. ).
Proposition
(characterization of epi/mono/iso (co-)unit of adjunction)
Let
be a pair of adjoint functors (Def. ).
Recall the definition of
-
adjunction unit/counit, from Def. )
-
faithful/fully faithful functor from Def.
-
mono/epi/isomorphism from Def. and Def. .
The following holds:
-
is faithful precisely if all components of the counit are epimorphisms ;
-
is faithful precisely if all components of the unit are monomorphisms
-
is full and faithful (exhibits a reflective subcategory, Def. ) precisely if all components of the counit are isomorphisms
-
is full and faithful (exhibits a coreflective subcategory, def. ) precisely if all component of the unit are isomorphisms .
Proof
This follows directly by Lemma , using the definition of epi/monomorphism (Def. ) and the characterization of isomorphism from Example .
To complete this pattern, we will see below in Prop. that following are equivalent:
-
the unit and counit are both natural isomorphism, hence and are both fully faithful;
-
is an equivalence (Def. );
-
is an equivalence (Def. )
-
is an adjoint equivalence (Def. ).
Proposition
(right/left adjoint functors preserve monomorphism/epimorphisms and terminal/initial objects)
Every right adjoint functor (Def. ) preserves
-
terminal objects (Def. ),
-
monomorphisms (Def. )
Every left adjoint functor (Def. ) preserves
-
initial objects (Def. ),
-
epimorphisms (Def. ).
Proof
This is immediate from the adjunction hom-isomorphism (10), but we spell it out:
We consider the first case, the second is formally dual (Example ). So let be a right adjoint functor with left adjoint .
Let be a terminal object (Def. ). We need to show that for every object the hom-set is a singleton. But by the hom-isomorphism (10) we have a bijection
where in the last step we used that is a terminal object, by assumption.
Next let be a monomorphism. We need to show that for any object, the hom-functor out of yields a monomorphism
Now consider the following naturality square (11) of the adjunction hom-isomorphism (10):
Here the right vertical function is an injective function, by assumption on and the definition of monomorphism. Since the two horizontal functions are bijections, this implies that also is an injection.
But the main preservation property of adjoint functors is that adjoints preserve (co-)limits. This we discuss as Prop. below, after introducing limits and colimits in Def. below.
Prop. says that adjoint functors are equivalenty “adjunctions in Cat”, as defined there. This is a special case of a general more abstract concept of adjunction, that is useful:
Definition
A strict category is
-
for each pair of objects, a small category (Def. ), called the hom-category from to .
We denote the objects of this hom-category by arrows like this:
and call them the 1-morphisms of ,
and we denote the morphisms in the hom-category by double arrows, like this:
and call these the 2-morphisms of ;
-
for each object a 1-morphism
called the identity morphism on ;
-
for each triple of objects, a functor (Def. )
from the product category (Example ) of hom-categories, called composition;
such that:
-
for all pairs of objects unitality holds:
the functors of composition with identity morphisms are identity functors
-
for all quadruples of objects composition satifies associativity, in that the following two composite functors are equal:
The archetypical example of a strict 2-category is the category of categories:
Example
There is a strict 2-category (Def. ) Cat whose
-
objects are small categories (Def. );
-
1-morphisms are functors (Def. );
-
2-morphisms are natural transformations (Def. )
with the evident composition operations.
With a concept of 2-category in hand, we may phrase Prop. more abstractly:
Definition
(adjunction in a 2-category)
Let be a strict 2-category (Def. ). Then an adjunction in is
-
called the left adjoint and right adjoint ;
-
, called the adjunction unit
, called the adjunction counit
such that the following triangle identities hold:

We denote this situation by
Hence via Example , Prop. says that an adjoint pair of functors is equivalente an adjunction in the general sense of Def. , realized in the very large strict 2-category Cat of categories.
This more abstract perspecive on adjunctions allow us now to understand “duality of dualities” as adjunction in a 2-category of adjunctions:
Example
(strict 2-category of categories with adjoint functors between them)
Let be the strict 2-category which is defined just as Cat (Def. ) but with the 1-morphisms being functors that are required to be left adjoints (Def. ).
Since adjoints are unique up to natural isomorphism (Prop. ), this may be thought of as a 2-category whose 1-morphisms are adjoint pairs of functors.
Example
(adjunctions of adjoint pairs are adjoint triples)
An adjunction (Def. ) in the 2-category of categories with adjoint functors between them (Example ) is equivalently an adjoint triple of functors (Remark ):
The adjunction says that two left adjoint functors and , which, hence each participate in an adjoint pair
form themselves an adjoint pair
By essentiall uniqueness of adjoints (Prop. ) this implies a natural isomorphism and hence an adjoint triple:
Example suggest to consider a slight variant of the concept of strict 2-categories which allows to make the duality between left adjoints and right adjoints explicit:
Definition
A double category is
-
a pair of categories , (Def. ) which share the same class of objects: , to be called the class of objects of
where the morphisms of are to be called the horizontal morphisms of ,
while the morphisms of are to be called the vertical morphisms of ,
-
for each quadruple of objects and pairs of pairs of horizontal/vertical morphisms of the form
a set , to be called the set of 2-morphisms of between the given 1-morphisms, whose elements we denote by
-
a horizontal and a vertical composition operation of 2-morphisms which is unitality and associative in both directions in the evident way, which respects composition in and , and such that horizontal and vertical composition commute over each other in the evident way.
Example
(double category of squares of a strict 2-category)
Let be a strict 2-category (Def. ). Then its double category of squares is the double category (Def. ) whose
-
objects are those of ;
-
horizontal morphisms and vertical morphisms are both the 1-morphisms of ;
-
are the 2-morphisms of between the evident composites of 1-morphisms:
and composition is given by the evident compositions in .
Remark
(strict and weak 2-functors)
Given two strict 2-categories (Def. ) or double categories (Def. ), , there is an evident notion of 2-functor or double functor
between them, namely functions on objects, 1-morphisms and 2-morphisms which respect all the composition operations and identity morphisms.
These are also called strict 2-functors.
This is in contrast to a more flexible concept of weak 2-functors, often called pseudofunctors, which respect composition of 1-morphisms only up to invertible 2-morphisms (which themselves are required to satisfy some coherence condition):
We will see an important example of a weak double functor in the construction of derived functors of Quillen functors, below in Prop. .
Equivalences
We have seen functors (Def. ) as the homomorphisms between categories (Def. ). But functors themselves are identified only up to natural isomorphism (Def. ), reflective the fact that they are the 1-morphisms in a 2-category of categories (Example ). This means that in identifying two categories, we should not just ask for isomorphisms between them, hence for a functor between them that has a strict inverse morphism, but just for an inverse up to natural isomorphism.
This is called an equivalence of categories (Def. below). A particularly well-behaved equivalence of categories is an equivalence exhibited by an adjoint pair of functors, called an adjoint equivalence of categories (Def. below). In fact every equivalence of categories may be improved to an adjoint equivalence (Prop. ).
Definition
(adjoint equivalence of categories)
Let , be two categories (Def. ). Then an adjoint equivalence of categories between them is a pair adjoint functors (Def. )
such that their unit and counit (Def. ) are natural isomorphisms (as opposed to just being natural transformations)
There is also the following, seemingly weaker, notion:
Definition
Let , be two categories (Def. ). Then an equivalence of categories
is a pair of functors back and forth, as shown (Def. ), together with natural isomorphisms (Def. ) between their composition and the identity functors:
If a functor participates in an equivalence of categories, that functor alone is usually already called an equivalence of categories. If there is any equivalence of categories between two categories, these categories are called equivalent.
Proposition
(every equivalence of categories comes from an adjoint equivalence of categories)
Let and be two categories (Def. ). Then the they are equivalent (Def. ) precisely if there exists an adjoint equivalence of categories between them (Def. ).
Moreover, let be a functor (Def. ) which participates in an equivalence of categories (Def. ). Then for every functor equipped with a natural isomorphism
there exists a natural isomorphism
which completes this to an adjoint equivalence of categories (Def. ).
Inside every adjunction sits its maximal adjoint equivalence:
Proposition
(fixed point equivalence of an adjunction)
Let
be a pair of adjoint functors (Def. ). Say that
-
an object is a fixed point of the adjunction if its adjunction unit (Def. ) is an isomorphism (Def. )
and write
for the full subcategory on these fixed objects (Example )
-
an object is a fixed point of the adjunction if its adjunction counit (Def. ) is an isomorphism (Def. )
and write
for the full subcategory on these fixed objects (Example )
Then the adjunction (co-)restrics to an adjoint equivalence (Def. ) on these full subcategories of fixed points
Proof
It is sufficient to see that the functors (co-)restrict as claimed, for then the restricted adjunction unit/counit are isomorphisms by definition, and hence exhibit an adjoint equivalence.
Hence we need to show that
-
for we have that is an isomorphism;
-
for we have that is an isomorphism.
For the first case we claim that provides an inverse: by the triangle identity (18) it is a right inverse, but by assumption it is itself an invertible morphism, which implies that is an isomorphism.
The second claim is formally dual.
Modalities
Generally, a full subcategory-inclusion (Def. ) may be thought of as a consistent proposition about objects in a category: The objects in the full subcategory are those that have the given property.
This basic situation becomes particularly interesting when the inclusion functor has a left adjoint or a right adjoint (Def. ), in which case one speaks of a reflective subcategory, or a coreflective subcategory, respectively (Def. below). The adjunction now implies that each object is reflected or coreflected into the subcategory, and equipped with a comparison morphism to or from its (co-)reflection (the adjunction (co-)unit, Def. ). This comparison morphism turns out to always be an idempotent (co-)projection, in a sense made precise by Prop. below.
This means that, while any object may not fully enjoy the property that defines the subcategory, one may ask for the “aspect” of it that does, which is what is (co-)projected out. Regarding objects only via these aspects of them hence means to regard them only locally (where they exhibit that aspect) or only in the mode of focus on this aspect. Therefore one also calls the (co-)reflection operation into the given subcategory a (co-)localization or (co-)modal operator, or modality, for short (Def. below).
One finds that (co-)modalities are a fully equivalent perspective on the (co-)reflective subcategories of their fully (co-)modal objects (Def. below), this is the statement of Prop. below.
Another alternative perspective on this situation is given by the concept of localization of categories (Def. below), which is about universally forcing a given collection of morphisms (“weak equivalences”, Def. below) to become invertible. A reflective localization is equivalently a reflective subcategory-inclusion (Prop. below), and this exhibits the modal objects (Def. below) as equivalently forming the full subcategory of local objects (Def. below).
Conversely, every reflection onto full subcategories of -local objects (Def. below) satisfies the universal property of a localization at with respect to left adjoint functors (Prop. below).
In conclusion, we have the following three equivalent perspectives on modalities.
| reflective subcategory | modal operator | reflective localization |
|---|---|---|
| object in reflective full subcategory | modal object | local object |
Definition
(reflective subcategory and coreflective subcategory)
Let be a category (Def. ) and
a full subcategory-inclusion (hence a fully faithful functor Def. ). This is called:
-
a reflective subcategory inclusion if the inclusion functor has a left adjoint def. )
then called the reflector;
-
a coreflective subcategory-inclusion if the inclusion functor has a right adjoint (def. )
then called the coreflector.
Example
(reflective subcategory inclusion of sets into small groupoids)
There is a reflective subcategory-inclusion (Def. )
of the category of sets (Example ) into the category Grpd (Example ) of small groupoids (Example ) where
-
the right adjoint full subcategory inclusion (Def. ) sends a set to the groupoid with set of objects being , and the only morphisms being the identity morphisms on these objects (also called the discrete groupoid on , but this terminology is ambiguous)
-
the left adjoint reflector sends a small groupoid to its set of connected components, namely to the set of equivalence classes under the equivalence relation on the set of objects, which regards two objects as equivalent, if there is any morphism between them.
We now re-consider the concept of reflective subcategories from the point of view of modalities:
Definition
(modality)
Let be a category (Def. ). Then
-
a modal operator on is
-
an endofunctor
whose full essential image we denote by
-
a natural transformation (Def. )
(23)for all objects , to be called the unit morphism;
such that:
-
for every object in the essential image of , every morphism into factors uniquely through the unit (23)
which equivalently means that if the operation of precomposition with the unit yields a bijection of hom-sets
(24)
-
-
a comodal operator on is
-
an endofunctor
whose full essential image we denote by
-
a natural transformation (Def. )
(25)for all objects , to be called the counit morphism;
such that:
-
for every object in the essential image of , every morphism out of factors uniquely through the counit (23)
which equivalently means that if the operation of postcomposition with the counit yields a bijection of hom-sets
(26)
-
Proposition
(modal operators equivalent to reflective subcategories)
If
is a reflective subcategory-inclusion (Def. ). Then the composite
equipped with the adjunction unit natural transformation (Def. )
is a modal operator on (Def. ).
Dually, if
is a coreflective subcategory-inclusion (Def. ). Then the composite
equipped with the adjunction counit natural transformation (Def. )
is a comodal operator on (Def. ).
Conversely:
If an endofunctor with natural transformation is a modal operator on a category (Def. ), then the inclusion of its full essential image is a reflective subcategory inclusion (Def. ) with reflector given by the corestriction of to its image:
Dually, if an endofunctor with natural transformation is a comodal operator (Def. ), then the inclusion of its full essential image is a coreflective subcategory inclusion (Def. ) with coreflector given by the corestriction of to its image
Proof
The first two statements are immedialy a special case of the characterization of adjunctions via universal morphisms in Prop. : Using that is here assumed to be fully faithful, the uniqueness of in the universal morphism-factorization condition (21)
implies that also is the unique morphism making that triangle commute.
Similarly for the converse: The assumption on a modal operator is just so as to make its unit be a universal morphism (Def. ) into the inclusion functor of its essential image.
Proposition
(modal operator is idempotent)
Let be a category (Def. ).
For a modal operator on , with unit (Def. ), it is idempotent, in that it is naturally isomorphic (Def. ) to the composition with itself:
In fact, the image under of its unit is such an isomorphism
as is its unit on its image
Formally dually, for a comodal operator on , with counit (Def. ), it is idempotent, in that it is naturally isomorphic (Def. ) to the composition with itsef:
In fact, the image under of its counit is such an isomorphism
as is its counit on its image
Proof
We discuss the first case, the second is formally dual (Example ).
By Prop. , the modal operator is equivalent to the composite obtained from the reflective subcategory-inclusion (Def. ) of its essential image of modal objects:
and its unit is the corresponding adjunction unit (Def. )
Hence it is sufficient to show that the morphisms and and are isomorphisms.
Now, the triangle identities (18) for the adjunction , which hold by Prop. , say that their composition with the adjunction counit is the identity morphism
But by Prop. , the counit is a natural isomorphism, since is fully faithful. Hence we may cancel it on both sides of the triangle identities and find that and are indeed isomorphisms.
Definition
Let be a category (Def. ).
For a modal operator on (Def. ), we say:
-
a -modal object is an object such that the following conditions hold (which are all equivalent, by Prop. ):
-
it is in the -essential image: ,
-
it is isomorphic to its own -image: ,
-
specifically its -unit is an isomorphism .
-
-
a -submodal object is an object , such that
- its -unit is a monomorphism (Def. ): .
Dually (Example ):
For a comodal operator on (Def. ), we say:
-
a -comodal object is an object such that the following conditions hold (which are all equivalent, by Prop. ):
-
it is in the -essential image: ,
-
it is isomorphic to its own -image: ,
-
specifically its -counit is an isomorphism
-
-
a -supcomodal object is an object , such that
- its -counit is an epimorphism (Def. ): .
Definition
Let
be an adjoint triple (Remark ) such that and are fully faithful functors (necessarily both, by Prop. ). By Prop. , there are induced modal operators
which themselves form am adjoint pair
hence called an adjoint modality. The adjunction unit and adjunction counit as in (13) may now be read as exhibiting each object in the domain of as “in between the opposite extremes of its -modal aspect and its -modal aspect”
A formally dual situation (Example ) arises when is fully faithful.
with
and canonical natural transformation between opposite extreme aspects given by
Proposition
(fully faithful adjoint triple)
Let be an adjoint triple (Remark ). Then the following are equivalent:
-
is a fully faithful functor;
-
is a fully faithful functor,
-
is an adjoint modality (Def. ).
For proof see this prop..
In order to analyze (in Prop. below) the comparison morphism of opposite extreme aspects (27) induced by an adjoint modality (Def. ), we need the following technical Lemma:
Lemma
Let
be an adjoint triple with induced adjoint modality (Def. ) to be denoted
Denoting the adjunction units/counits (Def. ) as
| adjunction | unit | counit |
|---|---|---|
we have that the following composites of unit/counit components are equal:
Proof
We claim that the following diagram commutes (Def. ):
This commutes, because:
-
the left square is the image under of naturality (4) for on ;
-
the top square is naturality (4) for on ;
-
the right square is naturality (4) for on ;
-
the bottom commuting triangle is the image under of the triangle identity (18) for on .
Moreover, notice that
-
the total bottom composite is the identity morphism , due to the triangle identity (18) for ;
-
also the other two morphisms in the bottom triangle are isomorphisms, as shown, due to the idempoency of the -adjunction (Prop. .)
Therefore the total composite from along the bottom part of the diagram equals the left hand side of (28), while the composite along the top part of the diagram clearly equals the right hand side of (28).
Proposition
(comparison transformation between opposite extremes of adjoint modality)
Consider an adjoint triple of the form
with induced adjoint modality (Def. ) to be denoted
Denoting the adjunction units/counits (Def. ) as
| adjunction | unit | counit |
|---|---|---|
Then for all the following two natural transformations, constructed from the adjunction units/counits (Def. ) and their inverse morphisms (using idempotency, Prop. ), are equal:
Moreover, the image of these morphisms under equals the following composite:
hence
Proof
The first statement follows directly from Lemma .
For the second statement, notice that the -adjunct (Prop. ) of
is
where under the braces we uses the triangle identity (Prop. ).
(As a side remark, for later usage, we observe that the morphisms on the left in (32) are isomorphisms, as shown, by idempotency of the adjunctions.)
From this we obtain the following commuting diagram:
Here:
-
on the left we identified by applying the formula (Prop. ) for -adjuncts to (32);
-
on the right we used the triangle identity (Prop. ) for .
This proves the second statement.
Definition
(preorder on modalities)
Let and be two modal operators on a category . By Prop. these are equivalently characterized by their reflective full subcategories of modal objects.
There is an evident preorder on full subcategories of , given by full inclusions of full subcategories into each other. We write if the full subcategory on the left is contained, as a full subcategory of , in that on the right. Via prop. there is the induced preorder on modal operators, and we write
There is an analogous preorder on comodal operators (Def. ).
If we have two adjoint modalities (Def. ) of the same type (both modal left adjoint or both comodal left adjoint) such that both the modalities and the comodalities are compatibly ordered in this way, we denote this situation as follows:
etc.
Example
(bottom and top adjoint modality)
Let be a category with both an initial object and a terminal object (Def. ). Then, by Example there is an adjoint triple between and the terminal category (Example ) of the form
The induced adjoint modality (Def. ) is
By slight abuse of notation, we will also write this as
On the other extreme, for any category whatsoever, the identity functor on it is adjoint functor to itself, and constitutes an adjoint modality (Def. )
Here
in the preorder on adjoint modalities according to Def. , in that for every adjoint modality of the form we have the following:
Definition
On some category , consider an inclusion of adjoint modalities, according to Def. :
We say:
Remark
For a progression of adjoint modalities of the form
the analog of Aufhebung (Def. ) is automatic, since, by Prop. , in this situation the full subcategories modal objects at each stage coincide already.
For emphasis we may denote this situation by
Example
(top adjoint modality provides Aufhebung of all oppositions)
For any category, the top adjoint modality (Def. ) provides Aufhebung (Def. ) of every other adjoint modality.
But already Aufhebung of the bottom adjoint modality is a non-trivial and interesting condition. We consider this below in Prop. .
We now re-consider the concept of reflective subcategories from the point of view of localization of categories:
Definition
(category with weak equivalences)
A category with weak equivalences is
-
a category (Def. )
-
a subcategory (i.e. sub-class of objects and morphisms that inherits the structure of a category)
such that the morphisms in
-
include all the isomorphisms of ,
-
satisfy two-out-of-three:
If for , any two composable morphisms in , two out of the set are in , then so is the third.
Definition
Let be a category with weak equivalences (Def. ). Then the localization of at is, if it exsists
such that
-
sends all morphisms in to isomorphisms (Def. ),
-
is universal with this property: If is any functor with this property, then it factors through , up to natural isomorphism (Def. ):
and any two such factorizations and are related by a unique natural isomorphism compatible with and :
Such a localization is called a reflective localization if the localization functor has a fully faithful right adjoint, exhibiting it as the reflection functor of a reflective subcategory-inclusion (Def. )
Proposition
(reflective subcategories are localizations)
Every reflective subcategory-inclusion (Def. )
is the reflective localization (Def. ) at the class of morphisms that are sent to isomorphisms by the reflector .
Proof
Let be a functor which inverts morphisms that are inverted by .
First we need to show that it factors through , up to natural isomorphism. But consider the following whiskering of the adjunction unit (Def. ) with :
By idempotency (Prop. ), the components of the adjunction unit are inverted by , and hence by assumption they are also inverted by , so that on the right the natural transformation is indeed a natural isomorphism.
It remains to show that this factorization is unique up to unique natural isomorphism. So consider any other factorization via a natural isomorphism . Pasting this now with the adjunction counit
exhibits a natural isomorphism between . Moreover, this is compatible with according to (35), due to the triangle identity (Prop. ):
Finally, since is essentially surjective functor, by idempotency (Prop. ), it is clear that this is the unique such natural isomorphism.
Definition
Let be a category (Def. ) and let be a set of morphisms. Then an object is called an -local object if for all the hom-functor (Def. ) from into yields a bijection
hence if every morphism extends uniquely along to :
We write
for the full subcategory (Example ) of -local objects.
Definition
(reflection onto full subcategory of local objects)
Let be a category and set be a sub-class of its morphisms. Then the reflection onto local -objects (often just called “localization at the collection ” is, if it exists, a left adjoint (Def. ) to the full subcategory-inclusion of the -local objects (36):
A class of examples is the following, which comes to its full nature (only) after passage to homotopy theory (Example below):
Definition
(homotopy localization of 1-categories)
Let be a category, let be an object, and consider the class of morphisms given by projection out of the Cartesian product with , of all objects :
If the corresponding reflection onto the full subcategory of local objects (Def. ) exists, we say this is homotopy localization at that object , and denote the modal operator corresponding to this (via Prop. ) by
Proposition
(reflective localization reflects onto full subcategory of local objects)
Let be a category with weak equivalences (Def. ). If its reflective localization (Def. ) exists
then is equivalently the inclusion of the full subcategory (Example ) on the -local objects (Def. ), and hence is equivalently reflection onto the -local objects, according to Def. .
Proof
We need to show that
-
every is -local,
-
every is -local precisely if it is isomorphic to an object in .
The first statement follows directly with the adjunction isomorphism (10):
and the fact that the hom-functor takes isomorphisms to bijections (Example ).
For the second statement, consider the case that is -local. Observe that then is also local with respect to the class
of all morphisms that are inverted by (the “saturated class of morphisms”): For consider the hom-functor to the opposite of the category of sets. By assumption on this takes elements in to isomorphisms. Hence, by the defining universal property of the localization-functor , it factors through , up to natural isomorphism.
Since, by idempotency (Prop. ), the adjunction unit is in , this implies that we have a bijection of the form
In particular the identity morphism has a preimage under this function, hence a left inverse to :
But by 2-out-of-3 this implies that . Since the first item above shows that is -local, this allows to apply this same kind of argument again,
to deduce that also has a left inverse . But since a left inverse that itself has a left inverse is in fact an inverse morphisms (this Lemma), this means that is an inverse morphism to , hence that is an isomorphism and hence that is isomorphic to an object in .
Conversely, if there is an isomorphism from to a morphism in the image of hence, by the first item, to a -local object, it follows immediatly that also is -local, since the hom-functor takes isomorphisms to bijections and since bijections satisfy 2-out-of-3.
Proposition
(reflection onto local objects is localization with respect to left adjoints)
Let be a category (Def. ) and let be a class of morphisms in . Then the reflection onto the -local objects (Def. ) satisfies, if it exists, the universal property of a localization of categories (Def. ) with respect to left adjoint functors inverting .
Proof
Write
for the reflective subcategory-inclusion of the -local objects.
Say that a morphism in is an -local morphism if for every -local object the hom-functor (Example ) from to yields a bijection . Notice that, by the Yoneda embedding for (Prop. ), the -local morphisms are precisely the morphisms that are taken to isomorphisms by the reflector (via Example ).
Now let
be a pair of adjoint functors, such that the left adjoint inverts the morphisms in . By the adjunction hom-isomorphism (10) it follows that takes values in -local objects. This in turn implies, now via the Yoneda embedding for , that inverts all -local morphisms, and hence all morphisms that are inverted by .
Thus the essentially unique factorization of through now follows by Prop. .
Basic notions of Categorical algebra
We have seen that the existence of Cartesian products in a category equips is with a functor of the form
which is directly analogous to the operation of multiplication in an associative algebra or even just in a semigroup (or monoid), just “categorified” (Example below). This is made precise by the concept of a monoidal category (Def. below).
This relation between category theory and algebra leads to the fields of categorical algebra and of universal algebra.
Here we are mainly interested in monoidal categories as a foundations for enriched category theory, to which we turn below.
Monoidal categories
Definition
An_monoidal category_ is a category (Def. ) equipped with
-
a functor (Def. )
out of the product category of with itself (Example ), called the tensor product,
-
an object
called the unit object or tensor unit,
-
a natural isomorphism (Def. )
called the associator,
-
called the left unitor, and a natural isomorphism
called the right unitor,
such that the following two kinds of diagrams commute, for all objects involved:
-
triangle identity:
-
the pentagon identity:
Example
Let be a category in which all finite products exist. Then becomes a monoidal category (Def. ) by
-
taking the tensor product to be the Cartesian product
-
taking the unit object to be the terminal object (Def. )
Monoidal categories of this form are called cartesian monoidal categories.
Lemma
(Kelly 64)
Let be a monoidal category, def. . Then the left and right unitors and satisfy the following conditions:
-
;
-
for all objects the following diagrams commutes:
and
For proof see at monoidal category this lemma and this lemma.
Remark
Just as for an associative algebra it is sufficient to demand and and in order to have that expressions of arbitrary length may be re-bracketed at will, so there is a coherence theorem for monoidal categories which states that all ways of freely composing the unitors and associators in a monoidal category (def. ) to go from one expression to another will coincide. Accordingly, much as one may drop the notation for the bracketing in an associative algebra altogether, so one may, with due care, reason about monoidal categories without always making all unitors and associators explicit.
(Here the qualifier “freely” means informally that we must not use any non-formal identification between objects, and formally it means that the diagram in question must be in the image of a strong monoidal functor from a free monoidal category. For example if in a particular monoidal category it so happens that the object is actually equal to , then the various ways of going from one expression to another using only associators and this equality no longer need to coincide.)
Definition
A braided monoidal category, is a monoidal category (def. ) equipped with a natural isomorphism (Def. )
called the braiding, such that the following two kinds of diagrams commute for all objects involved (“hexagon identities”):
and
where denotes the components of the associator of .
Definition
A symmetric monoidal category is a braided monoidal category (def. ) for which the braiding
satisfies the condition:
for all objects
Remark
In analogy to the coherence theorem for monoidal categories (remark ) there is a coherence theorem for symmetric monoidal categories (def. ), saying that every diagram built freely (see remark ) from associators, unitors and braidings such that both sides of the diagram correspond to the same permutation of objects, coincide.
Definition
(symmetric closed monoidal category)
Given a symmetric monoidal category with tensor product (def. ) it is called a closed monoidal category if for each the functor has a right adjoint, denoted
hence if there are natural bijections
for all objects .
Since for the case that is the tensor unit of this means that
the object is an enhancement of the ordinary hom-set to an object in . Accordingly, it is also called the internal hom between and .
The adjunction counit (Def. ) in this case is called the evaluation morphism
Example
(Set is a cartesian closed category)
The category Set of all sets (Example ) equipped with its cartesian monoidal category-structure (Example ) is a closed monoidal category (Def. ), hence a cartesian closed category. The Cartesian product is the original Cartesian product of sets, and the internal hom is the function set of functions from to
Example
(tensor product of abelian groups is closed monoidal category symmetric monoidal category-structure)
The category Ab of abelian groups (as in Example ) becomes a symmetric monoidal category (Def. ) with tensor product the actual tensor product of abelian groups and with tensor unit the additive group of integers. Again the associator, unitor and braiding isomorphism are the evident ones coming from the underlying sets.
This is a closed monoidal category with internal hom being the set of homomorphisms equipped with the pointwise group structure for then .
This is the archetypical case that motivates the notation “” for the pairing operation in a monoidal category.
Example
(Cat and Grpd are cartesian closed categories)
The category Cat (Example ) of all small categories (Example ) is a cartesian monoidal category-structure (Example ) with Cartesian product given by forming product categories (Example ).
Inside this, the full subcategory (Example ) Grpd (Example ) of all small groupoids (Example ) is itself a cartesian monoidal category-structure (Example ) with Cartesian product given by forming product categories (Example ).
In both cases this yields a closed monoidal category (Def. ), hence a cartesian closed category: the internal hom is given by the functor category construction (Example ).
Example
(categories of presheaves are cartesian closed)
Let be a category and write for its category of presheaves (Example ).
This is
-
a cartesian monoidal category (Example ), whose Cartesian product is given objectwise in by the Cartesian product in Set:
for , their Cartesian product exists and is given by
-
a cartesian closed category (Def. ), whose internal hom is given for by
Here denotes the Yoneda embedding and is the hom-functor on the category of presheaves.
Proof
The first statement is a special case of the general fact that limits of presheaves are computed objectwise (Example ).
For the second statement, first assume that does exist. Then by the adjunction hom-isomorphism (10) we have for any other presheaf a natural isomorphism of the form
This holds in particular for a representable presheaf (Example ) and so the Yoneda lemma (Prop. ) implies that if it exists, then must have the claimed form:
Hence it remains to show that this formula does make (40) hold generally.
For this we use the equivalent characterization of adjoint functors from Prop. , in terms of the adjunction counit providing a system of universal arrows (Def. ).
Define a would-be adjunction counit, hence a would-be evaluation morphism (39), by
Then it remains to show that for every morphism of presheaves of the form there is a unique morphism such that
The commutativity of this diagram means in components at that, that for all and we have
Hence this fixes the component when its first argument is the identity morphism . But let be any morphism and chase through the naturality diagram for :
This shows that is fixed to be given by
at least on those pairs such that is in the image of .
But, finally, is also natural in
which implies that (42) must hold generally. Hence naturality implies that (41) indeed has a unique solution.
The internal hom (Def. ) turns out to share all the abstract properties of the ordinary (external) hom-functor (Def. ), even though this is not completely manifest from its definition. We make this explicit by the following three propositions.
Proposition
For a closed monoidal category (Def. ), there is a unique functor (Def. ) out of the product category (Def. ) of with its opposite category (Def. )
such that for each it coincides with the internal hom (38) as a functor in the second variable, and such that there is a natural isomorphism
which is natural not only in and , but also in .
Proof
We have a natural isomorphism for each fixed , and hence in particular for fixed and fixed by (38). With this the statement follows by Prop. .
In fact the 3-variable adjunction from Prop. even holds internally:
Proposition
(internal tensor/hom-adjunction)
In a symmetric closed monoidal category (def. ) there are natural isomorphisms
whose image under (see also Example below) are the defining natural bijections of Prop. .
Proof
Let be any object. By applying the natural bijections from Prop. , there are composite natural bijections
Since this holds for all , the fully faithfulness of the Yoneda embedding (Prop. ) says that there is an isomorphism . Moreover, by taking in the above and using the left unitor isomorphisms and we get a commuting diagram
Also the key respect of the hom-functor for limits is inherited by internal hom-functors
Proposition
(internal hom preserves limits)
Let be a symmetric closed monoidal category with internal hom-bifunctor (Prop. ). Then this bifunctor preserves limits in the second variable, and sends colimits in the first variable to limits:
and
Proof
For any object, is a right adjoint by definition, and hence preserves limits by Prop. .
For the other case, let be a diagram in , and let be any object. Then there are isomorphisms
which are natural in , where we used that the ordinary hom-functor preserves limits (Prop. ), and that the left adjoint preserves colimits, since left adjoints preserve colimits (Prop. ).
Hence by the fully faithfulness of the Yoneda embedding, there is an isomorphism
Now that we have seen monoidal categories with various extra properties, we next look at functors which preserve these:
Definition
Let and be two monoidal categories (def. ). A lax monoidal functor between them is
-
a functor (Def. )
-
a morphism
(43) -
a natural transformation (Def. )
(44)for all
satisfying the following conditions:
-
(associativity) For all objects the following diagram commutes
where and denote the associators of the monoidal categories;
-
(unitality) For all the following diagrams commutes
and
where , , , denote the left and right unitors of the two monoidal categories, respectively.
If and alll are isomorphisms, then is called a strong monoidal functor.
If moreover and are equipped with the structure of braided monoidal categories (def. ) with braidings and , respectively, then the lax monoidal functor is called a braided monoidal functor if in addition the following diagram commutes for all objects
A homomorphism between two (braided) lax monoidal functors is a monoidal natural transformation, in that it is a natural transformation of the underlying functors
compatible with the product and the unit in that the following diagrams commute for all objects :
and
We write for the resulting category of lax monoidal functors between monoidal categories and , similarly for the category of braided monoidal functors between braided monoidal categories, and for the category of braided monoidal functors between symmetric monoidal categories.
Remark
In the literature the term “monoidal functor” often refers by default to what in def. is called a strong monoidal functor. But for the purpose of the discussion of functors with smash product below, it is crucial to admit the generality of lax monoidal functors.
If and are symmetric monoidal categories (def. ) then a braided monoidal functor (def. ) between them is often called a symmetric monoidal functor.
Proposition
For two composable lax monoidal functors (def. ) between monoidal categories, then their composite becomes a lax monoidal functor with structure morphisms
and
Algebras and modules
Definition
Given a monoidal category (Def. ), then a monoid internal to is
such that
-
(associativity) the following diagram commutes
where is the associator isomorphism of ;
-
(unitality) the following diagram commutes:
where and are the left and right unitor isomorphisms of .
Moreover, if has the structure of a symmetric monoidal category (def. ) with symmetric braiding , then a monoid as above is called a commutative monoid in if in addition
-
(commutativity) the following diagram commutes
A homomorphism of monoids is a morphism
in , such that the following two diagrams commute
and
Write for the category of monoids in , and for its full subcategory of commutative monoids.
Example
Given a monoidal category (Def. ), the tensor unit is a monoid in (def. ) with product given by either the left or right unitor
By lemma , these two morphisms coincide and define an associative product with unit the identity .
If is a symmetric monoidal category (def. ), then this monoid is a commutative monoid.
Example
Given a symmetric monoidal category (def. ), and given two commutative monoids (def. ), then the tensor product becomes itself a commutative monoid with unit morphism
(where the first isomorphism is, (lemma )) and with product morphism given by
(where we are notationally suppressing the associators and where denotes the braiding of ).
That this definition indeed satisfies associativity and commutativity follows from the corresponding properties of , and from the hexagon identities for the braiding (def. ) and from symmetry of the braiding.
Similarly one checks that for then the unit maps
and the product map
and the braiding
are monoid homomorphisms, with equipped with the above monoid structure.
Definition
Given a monoidal category (def. ), and given a monoid in (def. ), then a left module object in over is
such that
-
(unitality) the following diagram commutes:
where is the left unitor isomorphism of .
-
(action property) the following diagram commutes
A homomorphism of left -module objects
is a morphism
in , such that the following diagram commutes:
For the resulting category of modules of left -modules in with -module homomorphisms between them, we write
Example
Given a monoidal category (def. ) with the tensor unit regarded as a monoid in a monoidal category via example , then the left unitor
makes every object into a left module, according to def. , over . The action property holds due to lemma . This gives an equivalence of categories
of with the category of modules over its tensor unit.
Example
The archetypical case in which all these abstract concepts reduce to the basic familiar ones is the symmetric monoidal category Ab of abelian groups from example .
-
A commutative monoid in in (def. ) is equivalently a commutative ring .
-
An -module object in (def. ) is equivalently an -module;
-
The tensor product of -module objects (def. ) is the standard tensor product of modules.
-
The category of module objects (def. ) is the standard category of modules .
Example
Closely related to the example , but closer to the structure we will see below for spectra, are monoids in the category of chain complexes from example . These monoids are equivalently differential graded algebras.
Proposition
In the situation of def. , the monoid canonically becomes a left module over itself by setting . More generally, for any object, then naturally becomes a left -module by setting:
The -modules of this form are called free modules.
The free functor constructing free -modules is left adjoint to the forgetful functor which sends a module to the underlying object .
Proof
A homomorphism out of a free -module is a morphism in of the form
fitting into the diagram (where we are notationally suppressing the associator)
Consider the composite
i.e. the restriction of to the unit “in” . By definition, this fits into a commuting square of the form (where we are now notationally suppressing the associator and the unitor)
Pasting this square onto the top of the previous one yields
where now the left vertical composite is the identity, by the unit law in . This shows that is uniquely determined by via the relation
This natural bijection between and establishes the adjunction.
Definition
Given a closed symmetric monoidal category (def. , def. ), given a commutative monoid in (def. ), and given and two left -module objects (def.), then
-
the tensor product of modules is, if it exists, the coequalizer
and if preserves these coequalizers, then this is equipped with the left -action induced from the left -action on
-
the function module is, if it exists, the equalizer
equipped with the left -action that is induced by the left -action on via
(e.g. Hovey-Shipley-Smith 00, lemma 2.2.2 and lemma 2.2.8)
Proposition
Given a closed symmetric monoidal category (def. , def. ), and given a commutative monoid in (def. ). If all coequalizers exist in , then the tensor product of modules from def. makes the category of modules into a symmetric monoidal category, with tensor unit the object itself, regarded as an -module via prop. .
If moreover all equalizers exist, then this is a closed monoidal category (def. ) with internal hom given by the function modules of def. .
(e.g. Hovey-Shipley-Smith 00, lemma 2.2.2, lemma 2.2.8)
Proof sketch
The associators and braiding for are induced directly from those of and the universal property of coequalizers. That is the tensor unit for follows with the same kind of argument that we give in the proof of example below.
Example
For a monoid (def. ) in a symmetric monoidal category (def. ), the tensor product of modules (def. ) of two free modules (def. ) and always exists and is the free module over the tensor product in of the two generators:
Hence if has all coequalizers, so that the category of modules is a monoidal category (prop. ) then the free module functor (def. ) is a strong monoidal functor (def. )
Proof
It is sufficient to show that the diagram
is a coequalizer diagram (we are notationally suppressing the associators), hence that , hence that the claim holds for and .
To that end, we check the universal property of the coequalizer:
First observe that indeed coequalizes with , since this is just the associativity clause in def. . So for any other morphism with this property, we need to show that there is a unique morphism which makes this diagram commute:
We claim that
where the first morphism is the inverse of the right unitor of .
First to see that this does make the required triangle commute, consider the following pasting composite of commuting diagrams
Here the the top square is the naturality of the right unitor, the middle square commutes by the functoriality of the tensor product and the definition of the product category (Example ), while the commutativity of the bottom square is the assumption that coequalizes with .
Here the right vertical composite is , while, by unitality of , the left vertical composite is the identity on , Hence the diagram says that , which we needed to show.
It remains to see that is the unique morphism with this property for given . For that let be any other morphism with . Then consider the commuting diagram
where the top left triangle is the unitality condition and the two isomorphisms are the right unitor and its inverse. The commutativity of this diagram says that .
Definition
Given a monoidal category of modules as in prop. , then a monoid in (def. ) is called an -algebra.
Proposition
Given a monoidal category of modules in a monoidal category as in prop. , and an -algebra (def. ), then there is an equivalence of categories
between the category of commutative monoids in and the coslice category of commutative monoids in under , hence between commutative -algebras in and commutative monoids in that are equipped with a homomorphism of monoids .
(e.g. EKMM 97, VII lemma 1.3)
Proof
In one direction, consider a -algebra with unit and product . There is the underlying product
By considering a diagram of such coequalizer diagrams with middle vertical morphism , one find that this is a unit for and that is a commutative monoid in .
Then consider the two conditions on the unit . First of all this is an -module homomorphism, which means that
commutes. Moreover it satisfies the unit property
By forgetting the tensor product over , the latter gives
where the top vertical morphisms on the left the canonical coequalizers, which identifies the vertical composites on the right as shown. Hence this may be pasted to the square above, to yield a commuting square
This shows that the unit is a homomorphism of monoids .
Now for the converse direction, assume that and are two commutative monoids in with a monoid homomorphism. Then inherits a left -module structure by
By commutativity and associativity it follows that coequalizes the two induced morphisms . Hence the universal property of the coequalizer gives a factorization through some . This shows that is a commutative -algebra.
Finally one checks that these two constructions are inverses to each other, up to isomorphism.
Definition
Let and be two monoidal categories (def. ). A lax monoidal functor between them is
satisfying the following conditions:
-
(associativity) For all objects the following diagram commutes
where and denote the associators of the monoidal categories;
-
(unitality) For all the following diagrams commutes
and
where , , , denote the left and right unitors of the two monoidal categories, respectively.
If and alll are isomorphisms, then is called a strong monoidal functor.
If moreover and are equipped with the structure of braided monoidal categories (def. ) with braidings and , respectively, then the lax monoidal functor is called a braided monoidal functor if in addition the following diagram commutes for all objects
A homomorphism between two (braided) lax monoidal functors is a monoidal natural transformation, in that it is a natural transformation of the underlying functors
compatible with the product and the unit in that the following diagrams commute for all objects :
and
We write for the resulting category of lax monoidal functors between monoidal categories and , similarly for the category of braided monoidal functors between braided monoidal categories, and for the category of braided monoidal functors between symmetric monoidal categories.
Remark
In the literature the term “monoidal functor” often refers by default to what in def. is called a strong monoidal functor. But for the purpose of the discussion of functors with smash product below, it is crucial to admit the generality of lax monoidal functors.
If and are symmetric monoidal categories (def. ) then a braided monoidal functor (def. ) between them is often called a symmetric monoidal functor.
Proposition
For two composable lax monoidal functors (def. ) between monoidal categories, then their composite becomes a lax monoidal functor with structure morphisms
and
Proposition
(lax monoidal functors preserve monoids)
Let and be two monoidal categories (def. ) and let be a lax monoidal functor (def. ) between them.
Then for a monoid in (def. ), its image becomes a monoid by setting
(where the first morphism is the structure morphism of ) and setting
(where again the first morphism is the corresponding structure morphism of ).
This construction extends to a functor
from the category of monoids of (def. ) to that of .
Moreover, if and are symmetric monoidal categories (def. ) and is a braided monoidal functor (def. ) and is a commutative monoid (def. ) then so is , and this construction extends to a functor between categories of commutative monoids:
Proof
This follows immediately from combining the associativity and unitality (and symmetry) constraints of with those of .
Enriched categories
The plain definition of categories in Def. is phrased in terms of sets. Via Example this assigns a special role to the category Set of all sets, as the “base” on top, or the “cosmos” inside which category theory takes place. For instance, the fact that hom-sets in a plain category are indeed sets, is what makes the hom-functor (Example ) take values in Set, and this, in turn, governs the form of the all-important Yoneda lemma (Prop. ) and Yoneda embedding (Prop. ) as statements about presheaves of sets (Example ).
At the same time, category theory witnesses the utility of abstracting away from concrete choices to their abstract properties that are actually used in constructions. This makes it natural to ask if one could replace the category Set by some other category which could similarly serve as a “cosmos” inside which category theory may be developed.
Indeed, such -enriched category theory (see Example below for the terminology) exists, beginning with the concept of -enriched categories (Def. below) and from there directly paralleling, hence generalizing, plain category theory, as long as one assumes the “cosmos” category to share a minimum of abstract properties with Set (Def. below).
This turns out to be most useful. In fact, the perspective of enriched categories is helpful already when Set, in which case it reproduces plain category theory (Example below), for instance in that it puts the (co)limits of the special form of (co)ends (Def. below) to the forefront (discussed below).
Definition
(cosmos)
A Bénabou cosmos for enriched category theory, or just cosmos, for short, is a symmetric (Def. ) closed monoidal category (Def. ) which has all limits and colimits.
Example
(examples of cosmoi for enriched category theory)
The following are examples of cosmoi (Def. ):
-
the sheaf topos (Def. ) over any site (Def. ) – by Prop. below.
In particular:
-
Set (Def. ) equipped with its cartesian closed category-structure (Example )
-
sSet (Def. , Prop. )
-
-
Grpd (Def. ) equipped with its cartesian closed category-structure (Example ).
-
Cat (Def. ) equipped with its cartesian closed category-structure (Example ).
Example
underlying set of an object in a cosmos
Let be a cosmos (Def. ), with its tensor unit (Def. ). Then the hom-functor (Def. ) out of
admits the structure of a lax monoidal functor (Def. ) to Set, with the latter regarded with its cartesian monoidal structure from Example .
Given , we call
also the underlying set of .
Proof
Take the monoidal transformations (eq“MonoidalComponentsOfMonoidalFunctor) to be
and take the unit transformation (43)
to pick .
Example
(underlying set of internal hom is hom-set)*
For a cosmos (Def. ), let be two objects. Then the underlying set (Def. ) of their internal hom (Def. ) is the hom-set (Def. ):
This identification is the adjunction isomorphism (10) for the internal hom adjunction (38) followed composed with a unitor (Def. ).
Definition
For a cosmos (Def. ), a -enriched category is:
-
for each , an object
called the -object of morphisms between and ;
-
for each a morphism in
out of the tensor product of hom-objects, called the composition operation;
-
for each a morphism , called the identity morphism on
such that the composition is associative and unital.
If the class happens to be a set (hence a small set instead of a proper class) then we say the -enriched category is small, as in Def. .
Example
(Set-enriched categories are plain categories)
An enriched category (Def. ) over the cosmos Set, as in Example , is the same as a plain category (Def. ).
Example
(Cat-enriched categories are strict 2-categories)
An enriched category (Def. ) over the cosmos Cat, as in Example , is the same as a strict 2-category (Def. ).
Example
(underlying category of an enriched category)
Let be a -enriched category (Def. ).
Using the lax monoidal structure (Def. ) on the hom functor (Example )
out of the tensor unit this induces a Set-enriched category with hence an ordinary category (Example ), with
-
;
-
.
It is in this sense that is a plain category equipped with extra structure, and hence an “enriched category”.
The archetypical example is itself:
Example
( as a -enriched category)
Evert cosmos (Def. ) canonically obtains the structure of a -enriched category, def. :
the hom-objects are the internal homs
and with composition
given by the adjunct under the (Cartesian product internal hom)-adjunction of the evaluation morphisms
The usual construction on categories, such as that of opposite categories (Def. ) and product categories (Def. ) have evident enriched analogs
Definition
(enriched opposite category and product category)
For a cosmos, let be -enriched categories (Def. ).
-
The opposite enriched category is the enriched category with the same objects as , with hom-objects
and with composition given by braiding (37) followed by the composition in :
-
the enriched product category is the enriched category whose objects are pairs of objects with and , whose hom-spaces are the tensor product of the separate hom objects
and whose composition operation is the braiding (37) followed by the tensor product of the separate composition operations:
Definition
For a cosmos (Def. ), let and be two -enriched categories (Def. ).
A -enriched functor from to
is
-
a function
of objects;
-
for each a morphism in
between hom-objects
such that this preserves composition and identity morphisms in the evident sense.
Example
For a cosmos (Def. ), let be a -enriched category (Def. ). Then there is a -enriched functor out of the enriched product category of with its enriched opposite category (Def. )
to , regarded as a -enriched category (Example ), which sends a pair of objects to the hom-object , and which acts on morphisms by composition in the evident way.
Example
For a cosmos (Def. ), let be a -enriched category (Def. ). Then a -enriched functor (Def. )
to the archetypical -enriched category from Example is:
-
an object for each object ;
-
a morphism in of the form
for all pairs of objects
(this is the adjunct of under the adjunction (38) on )
such that composition is respected, in the evident sense.
For every object , there is an enriched representable functor, denoted
(where on the right we have the enriched hom-functor from Example )
which sends objects to
and whose action on morphisms is, under the above identification, just the composition operation in .
More generally, the following situation will be of interest:
Example
(enriched functor on enriched product category with opposite category)
An -enriched functor (Def. ) into (Example ) out of an enriched product category (Def. )
(an “enriched bifunctor”) has component morphisms of the form
By functoriality and under passing to adjuncts (Def. ) under (38) this is equivalent to two commuting actions
and
In the special case of a functor out of the enriched product category of some -enriched category with its enriched opposite category (def. )
then this takes the form of a “pullback action” in the first variable
and a “pushforward action” in the second variable
Definition
(enriched natural transformation)
For a cosmos (Def. ), let and be two -enriched categories (Def. ) and let
be two -enriched functors (Def. ) from to .
Then a -enriched natural transformation
is
and
agree.
Example
(functor category of enriched functors)
For a cosmos (Def. ) let , be two -enriched categories (Def. ). Then there is a category (Def. ) of enriched functors (Def. ), to be denoted
whose objects are the enriched functors and whose morphisms are the enriched natural transformations between these (Def. ).
In the case that Set, via Def. , with -enriched categories identified with plain categories via Example , this coincides with the functor category from Example .
Notice that, at this point, is a plain category, not itself a -enriched category, unless Set. But it may be enhanced to one, this is Def. below.
There is now the following evident generalization of the concept of adjoint functors (Def. ) from plain category theory to enriched category theory:
Definition
For a cosmos (Def. ), let , be two -enriched categories (Def. ). Then an adjoint pair of -enriched functors or enriched adjunction
is a pair of -enriched functors (Def. ), as shown, such that there is a -enriched natural isomorphism (Def. ) between enriched hom-functors (Def. ) of the form
Definition
(enriched equivalence of categories)
For a cosmos (Def. ), let , be two -enriched categories (Def. ). Then an equivalence of enriched categories
is a pair of -enriched functors back and forth, as shown (Def. ), together with -enriched natural isomorphisms (Def. ) between their composition and the identity functors:
Universal constructions
What makes category theory be theory, as opposed to just a language, is the concept of universal constructions. This refers to the idea of objects with a prescribed property which are universal with this property, in that they “know about” or “subsume” every other object with that same kind of property. Category theory allows to make precise what this means, and then to discover and prove theorems about it.
Universal constructions are all over the place in mathematics. Iteratively finding the universal constructions in a prescribed situation essentially amounts to systematically following the unravelling of the given situation or problem or theory that one is studying.
There are several different formulations of the concept of universal constructions, discussed below:
But these three kinds of constructions all turn out to be special cases of each other, hence they really reflect different perspectives on a single topic of universal constructions. In fact, all three are also special cases of the concept of adjunction (Def. ), thus re-amplifying that category theory is really the theory of adjunctions and hence, if we follow (Lambek 82), of duality.
Limits and colimits
Maybe the most hands-on version of universal constructions are limits (Def. below), which is short for limiting cones (Remark below). The formally dual concept (Example ) is called colimits (which are hence limits in an opposite category). Other terminology is in use, too:
| limit | colimit |
| inverse limit | direct limit |
There is a variety of different kinds of limits/colimits, depending on the diagram shape that they are limiting (co-)cones over. This includes universal constructions known as equalizers, products, fiber products/pullbacks, filtered limits and various others, all of which are basic tools frequently used whenever category theory applies.
A key fact of category theory, regarding limits, is that right adjoints preserve limits and left adjoints preserve colimits (Prop. below). This will be used all the time. A partial converse to this statement is that if a functor preserves limits/colimits, then its adjoint functor is, if it exists, objectwise given by a limit/colimit over a comma category under/over the given functor (Prop. below). Since these comma categories are in general not small, this involves set-theoretic size subtleties that are dealt with by the adjoint functor theorem (Remark below). We discuss in detail a very special but also very useful special case of this in Prop. , further below.
Definition
Let be a small category (Def. ), and let be any category (Def. ). In this case one also says that a functor
is a diagram of shape in .
Recalling the functor category (Example ) , there is the constant diagram-functor
which sends an object to the functor that sends every to , and every morphism in to the identity morphism on . Accordingly, every morphism in is sent by to the natural transformation (Def. ) all whose components are equal to that morphism.
Now:
-
if has a right adjoint (Def. ), this is called the construction of forming the limiting cone of -shaped diagrams in , or just limit (or inverse limit) for short, and denoted
-
if has a left adjoint (Def. ), this is called the construction of forming the colimiting cocone of -shaped diagrams in , or just colimit (or direct limit) for short, and denoted
If () exists for a given , one says that has all limits (_has all colimits_) of shape _ or that all limits (colimits) of shape exist in . If this is the case for all small diagrams , one says that has all limits (_has all colimits_) or that all limits exist in , (_all colimits exist in .)
Remark
Unwinding Definition of limits and colimits, it says the following.
First of all, for any object and any functor, a natural transformation (Def. ) of the form
has component morphisms
in , for each , and the naturality condition (4) says that these form a commuting diagram (Def. ) of the form
for each morphism in . Due to the look of this diagram, one also calls such a natural transformation a cone over the functor .
Now the counit (Def. ) of the -adjunction (48) is a natural transformation of the form
and hence is, in components, a cone (50) over :
to be called the limiting cone over
But the universal property of adjunctions says that this is a very special cone: By Prop. the defining property of the limit is equivalently that for every natural transformation of the form (49), hence for every cone of the form (50), there is a unique natural transformation
which, due to constancy of the two functors applied in the naturality condition (4), has a constant component morphism
such that
hence such that (52) factors the given cone (50) through the special cone (51):
In this case one also says that is a morphism of cones.
Hence a limit cone is a cone over , such that every other cone factors through it in a unique way.
Of course this concept of (co)limiting cone over a functor makes sense also when
-
is not small,
-
and/or when a (co-)limiting cone exists only for some but not for all functors of this form.
Example
(terminal/initial object is empty limit/colimit)
Let be a category, and let be an object. The following are equivalent:
-
is a terminal object of (Def. );
And formally dual (example ): Let be an object. The following are equivalent:
-
is an initial object of (Def. );
Proof
We discuss the case of the terminal object, the other case is formally dual (Example ).
It suffices to observe that a cone over the empty diagram (Remark ) is clearly just a plain object of . Hence a morphism of such cones is just a plain morphism of . This way the condition on a limiting cone is now manifestly the same as the condition on a terminal object.
Example
(initial object is limit over identity functor)
Let be a category, and let be an object. The following are equivalent:
-
is an initial object of (Def. );
-
is the tip of a limit cone (Remark ) over the identity functor on .
Proof
First let be an initial object. Then, by definition, it is the tip of a unique cone over the identity functor
We need to show that that every other cone
factors uniquely through .
First of all, since the cones are over the identity functor, there is the component , and it is a morphism of cones.
To see that this is the unique morphism of cones, consider any morphism of cones , hence a morphism in such that for all . Taking here yields
where under the brace we used that is initial. This proves that is the limiting cone.
For the converse, assume now that is a limiting cone over the identity functor, with labels as in (53). We need to show that its tip is an initial object.
Now the cone condition applied for any object over the morphims says that
which means that constitutes a morphism of cones from to itself. But since is assumed to be a limiting cone, and since the identity morphism on is of course also a morphism of cones from to itsely, we deduce that
Now consider any morphism of the form . Since we already have the morphism , to show initiality of we need to show that .
Indeed, the cone condition of applied to now yields
where under the brace we used (54).
Example
(limits of presheaves are computed objectwise)
Let be a category and write for its category of presheaves (Example ). Let moreover be a small category and consider any functor
hence a -shaped diagram in the category of presheaves.
Then
Proof
We discuss the case of limits, the other case is formally dual (Example ).
Observe that there is a canonical equivalence (Def. )
where is the product category.
This makes manifest that a functor is equivalently a diagram of the form
Then observe that taking the limit of each “horizontal row” in such a diagram indead does yield a presheaf on , in that the construction extends from objects to morphisms, and uniquely so: This is because for any morphism in , a cone over (Remark ) induces a cone over , by vertical composition with
From this, the universal property of limits of sets (as in Remark ) implies that there is a unique morphism between the pointwise limits which constitutes a presheaf over
and that is the tip of a cone over the diagram in presheaves.
Hence it remains to see that this cone of presheaves is indeed universal.
Now if is any other cone over in the category of presheaves, then by the universal property of the pointswise limits, there is for each a unique morphism of cones in sets
Hence there is at most one morphisms of cones of presheaves, namely if these components make all their naturality squares commute.
But since everything else commutes, the two ways of going around this diagram constitute two morphisms from a cone over to the limit cone over , and hence they must be equal, by the universal property of limits.
Proposition
(hom-functor preserves limits)
Let be a category and write
for its hom-functor. This preserves limits (Def. ) in both its arguments (recalling that a limit in the opposite category is a colimit in ).
More in detail, let be a diagram. Then:
-
If the limit exists in then for all there is a natural isomorphism
where on the right we have the limit over the diagram of hom-sets given by
-
If the colimit exists in then for all there is a natural isomorphism
where on the right we have the limit over the diagram of hom-sets given by
Proof
We give the proof of the first statement, the proof of the second statement is formally dual (Example ).
First observe that, by the very definition of limiting cones, maps out of some into them are in natural bijection with the set of cones over the diagram with tip :
Hence it remains to show that there is also a natural bijection like so:
Now, again by the very definition of limiting cones, a single element in the limit on the right is equivalently a cone of the form
This is equivalently for each object a choice of morphism , such that for each pair of objects and each we have . And indeed, this is precisely the characterization of an element in the set .
Example
(initial and terminal object in terms of adjunction)
Let be a category (Def. ).
-
The following are equivalent:
-
has a terminal object (Def. );
-
the unique functor (Def. ) to the terminal category (Example ) has a right adjoint (Def. )
Under this equivalence, the terminal object is identified with the image under the right adjoint of the unique object of the terminal category.
-
-
Dually, the following are equivalent:
-
has an initial object (Def. );
-
the unique functor to the terminal category has a left adjoint
Under this equivalence, the initial object is identified with the image under the left adjoint of the unique object of the terminal category.
-
Proof
Since the unique hom-set in the terminal category is the singleton, the hom-isomorphism (10) characterizing the adjoint functors is directly the universal property of an initial object in
or of a terminal object
respectively.
Proposition
(left adjoints preserve colimits and right adjoints preserve limits)
Let be a pair of adjoint functors (Def. ). Then
Proof
Let be a diagram whose limit exists. Then we have a sequence of natural isomorphisms, natural in
where we used the hom-isomorphism (10) and the fact that any hom-functor preserves limits (Def. ). Because this is natural in the Yoneda lemma implies that we have an isomorphism
The argument that shows the preservation of colimits by is analogous.
Proposition
Let and be small categories (Def. ) and let be a category (Def. ) which admits limits (Def. ) of shape as well as limits of shape . Then these limits “commute” with each other, in that for a functor (hence a diagram of shape the product category), with corresponding adjunct functors (via Example )
we have that the canonical comparison morphism
is an isomorphism.
Proof
Since the limit-construction is the right adjoint functor to the constant diagram-functor, this is a special case of right adjoints preserve limits (Prop. ).
See limits and colimits by example for what formula (55) says for instance for the special case Set.
Remark
(general non-commutativity of limits with colimits)
In general limits do not commute with colimits. But under a number of special conditions of interest they do. Special cases and concrete examples are discussed at commutativity of limits and colimits.
Proposition
(pointwise expression of left adjoints in terms of limits over comma categories)
A functor (Def. ) has a left adjoint (Def. ) precisely if
-
for each object , the limit (Def. ) of the canonical functor (22) out of the comma category (Example )
exists.
In this case the value of the left adjoint on is given by that limit:
Proof
First assume that the left adjoint exist. Then
-
is a right adjoint and hence preserves limits since all right adjoints preserve limits (Prop. );
-
by Prop. the adjunction unit provides a universal morphism into , and hence, by Prop. , exhibits as the initial object of the comma category . The limit over any category with an initial object exists, as it is given by that initial object.
Conversely, assume that the two conditions are satisfied and let be given by (56). We need to show that this yields a left adjoint.
By the assumption that preserves all limits that exist, we have
Since the constitute a cone over the diagram of the , there is universal morphism
By Prop. it is now sufficient to show that is a universal morphism into , hence that for all and there is a unique morphism such that
By Prop. , this is equivalent to being the initial object in the comma category , which in turn is equivalent to it being the limit of the identity functor on (by Example ). But this follows directly from the limit formulas (56) and (57).
Remark
Beware the subtle point in Prop. , that the comma category is in general not a small category (Def. ): It has typically “as many” objects as has, and is not assumed to be small (while of course it may happen to be). But typical categories, such as notably the category of sets (Example ) are generally guaranteed only to admit limits over small categories. For this reason, Prop. is rarely useful for finding an adjoint functor which is not already established to exist by other means.
But there are good sufficient conditions known, on top of the condition that preserves limits, which guarantee the existence of an adjoint functor, after all. This is the topic of the adjoint functor theorem (one of the rare instances of useful and non-trivial theorems in mathematics for which issues of set theoretic size play a crucial role for their statement and proof).
A very special but also very useful case of the adjoint functor theorem is the existence of adjoints of base change functors between categories of (enriched) presheaves via Kan extension. This we discuss as Prop. below. Since this is most conveniently phrased in terms of special limits/colimits called ends/coends (Def. below) we first discuss these.
Ends and coends
For working with enriched categories (Def. ) , a certain shape of limits/colimits (Def. ) is particularly relevant: these are called ends and coends (Def. below). We here introduce these and then derive some of their basic properties, such as notably the expression for Kan extension in terms of (co-)ends (prop. below).
Definition
((co)end)
Let be a small -enriched category (Def. ). Let
be an enriched functor (Def. ) out of the enriched product category of with its opposite category (Def. ). Then:
Example
For a cosmos, let be a group object. There is the n the one-object -enriched category as in Example .
Then a -enriched functor
is an object equipped with a morphism
satisfying the action property. Hence this is equivalently an action of on .
The opposite category (def. ) comes from the opposite group-object
(The isomorphism induces a canonical euqivalence of enriched categories .)
So an enriched functor
is equivalently a right action of .
Therefore the coend of two such functors (def. ) coequalizes the relation
(where juxtaposition denotes left/right action) and is the quotient of the plain tensor product by the diagonal action of the group :
Example
(enriched natural transformations as ends)
Let be a small enriched category (Def. ). For two enriched presheaves (Example ), the end (def. ) of the internal-hom-functor
is an object of whose underlying set (Example ) is the set of enriched natural transformations (Def. )
Proof
The underlying pointed set functor preserves all limits, since hom-functors preserve limits (Prop. ). Therefore there is an equalizer diagram in Set of the form
where we used Example to identify underlying sets of internal homs with hom-sets.
Here the object in the middle is just the set of indexed sets of component morphisms . The two parallel maps in the equalizer diagram take such a collection to the indexed set of composites (45) and (46). Hence that these two are equalized is precisely the condition that the indexed set of components constitutes an enriched natural transformation.
Conversely, example says that ends over bifunctors of the form constitute hom-spaces between pointed topologically enriched functors:
Definition
For a cosmos (Def. ), let be a small -enriched category (Def. ).
Then the -enriched presheaf category is -enriched functor category from to , hence is the following -enriched category (Def. )
-
the objects are the -enriched functors (Def. );
-
the hom-objects are the ends
(58) -
the composition operation on these is defined to be the one induced by the composite maps
where the first morphism is degreewise given by projection out of the limits that defined the ends. This composite evidently equalizes the two relevant adjunct actions (as in the proof of example ) and hence defines a map into the end
By Example , the underlying plain category (Example ) of this enriched functor category is the plain functor category of enriched functors from Example .
Proposition
For a cosmos (Def. ) let be a small enriched category (Def. ). For an enriched presheaf (Example ) and for an object, there is a natural isomorphism
between the hom-object of the enriched functor category (Def. ), from the functor represented by to , and the value of on .
In terms of the ends (def. ) defining these hom-objects (58), this means that
In this form the statement is also known as Yoneda reduction.
Now that natural transformations are expressed in terms of ends (example ), as is the enriched Yoneda lemma (prop. ), it is natural to consider the dual statement (Example ) involving coends:
Proposition
For a cosmos (Def. ), let be a small -enriched category (Def. ). For an enriched presheaf (Def. ) and for an object, there is a natural isomorphism
Moreover, the morphism that hence exhibits as the coequalizer of the two morphisms in def. is componentwise the canonical action
which is adjunct to the component map of the enriched functor .
(e.g. MMSS 00, lemma 1.6)
Proof
By the definition of coends and the universal property of colimits, enriched natural transformations of the form
are in natural bijection with systems of component morphisms
which satisfy some compatibility conditions in their dependence on and (natural in and “extranatural” in ). By the internal hom adjunction, these are in natural bijection to systems of morphisms of the form
satisfying the analogous compatibility conditions. By Example these are in natural bijection with systems of morphisms
natural in
By the enriched Yoneda lemma (Prop. ), these, finally, are in natural bijection with systems of morphisms
natural in . Moreover, all these identifications are also natural in . Therefore, in summary, this shows that there is a natural isomorphism
With this, the ordinary Yoneda lemma (Prop. ) in the form of the Yoneda embedding of implies the required isomorphism.
Example
(co-Yoneda lemma over Set)
Consider the co-Yoneda lemma (Prop. ) in the special case Set (Example ).
In this case the coequalizer in question is the set of equivalence classes of pairs
where two such pairs
are regarded as equivalent if there exists
such that
(Because then the two pairs are the two images of the pair under the two morphisms being coequalized.)
But now considering the case that and , so that shows that any pair
is identified, in the coequalizer, with the pair
hence with .
As a conceptually important corollary we obtain:
Proposition
(category of presheaves is free co-completion)
For a small category (Def. ), its Yoneda embedding (Prop. ) exhibits the category of presheaves (Example ) as the free co-completion of under forming colimits (Def. ), in that it is a universal morphism, as in Def. but “up to natural isomorphism”, into a category with all colimits (by Example ) in the following sense:
there is a functor , unique up to natural isomorphism such that
-
extends through the Yoneda embedding, in that the following diagram commutes, up to natural isomorphism (Def. ):
Hence when interpreting presheaves as generalized spaces, this says that “generalized spaces are precisely what is obtained from allowing arbitrary gluings of ordinary spaces”, see also Remark below.
Proof
The last condition says that is fixed on representable presheaves by
and in fact naturally so:
But the co-Yoneda lemma (Prop. ) expresses every presheaf as a colimit of representable presheaves (in the special case of enrichment over , Example )
Since is required to preserve any colimit and hence these particular colimits, (59) implies that is fixed to act, up to isomorphism, as
(where the colimit on the right is computed in !).
Remark
The statement of the co-Yoneda lemma in prop. is a kind of categorification of the following statement in analysis (whence the notation with the integral signs):
For a topological space, a continuous function and denoting the Dirac distribution, then
It is this analogy that gives the name to the following statement:
Proposition
(Fubini theorem for (co)-ends)
For a cosmos (Def. ), let be two -enriched categories (Def. ) and
a -enriched functor (Def. ) from the product category with opposite categories (Def. ), as shown.
Then its end and coend (def. ) is equivalently formed consecutively over each variable, in either order:
and
Remark
(internal hom preserves ends)
Let be a cosmos (Def. ). Since the internal hom-functor in (Def. ) preserves limits in both variables (Prop. ), in particular it preserves ends (Def. ) in the second variable, and sends coends in the second variable to ends:
For all small -enriched categories, -enriched functors (Def. ) and all objects we have natural isomorphisms
and
With this coend calculus in hand, there is an elegant proof of the defining universal property of the smash tensoring and powering enriched presheaves
Definition
(tensoring and powering of enriched presheaves)
Let be a -enriched category, def. , with its functor category of enriched functors (Example ).
-
Define a functor
by forming objectwise tensor products
This is called the tensoring of over .
-
Define a functor
by forming objectwise internal homs (Def. )
This is called the powering of over .
Proposition
(universal property of tensoring and powering of enriched presheaves)
For a cosmos (Def. ), let be a small -enriched category (Def. ), with the corresponding enriched presheaf category.
Then there are natural isomorphisms
and
for all and all , where is the powering and the tensoring from Def. .
In particular there is the composite natural isomorphism
exhibiting a pair of adjoint functors
Proof
Via the end-expression for from Example , and the fact (remark ) that the internal hom-functor ends in the second variable, this reduces to the fact that is the internal hom in the closed monoidal category (Example ) and hence satisfies the internal tensor/hom-adjunction isomorphism (prop. ):
and
Tensoring and cotensoring
We make explicit the general concept of which Prpp. provides a key class of examples:
Definition
(tensoring and cotensoring)
For a cosmos (Def. ) let be a -enriched category (Def. ). Recall the enriched hom-functors (Example )
-
A powering (or cotensoring) of over is
-
a functor (Def. )
-
for each a natural isomorphism (Def. ) of the form
(61)
-
-
A copowering (or tensoring) of over is
-
a functor (Def. )
-
for each a natural isomorphism (Def. ) of the form
(62)
-
If is equipped with a (co-)powering it is called (co-)powered over .
Proposition
(tensoring left adjoint to cotensoring)
For a cosmos (Def. ) let be a -enriched category (Def. ).
If is both tensored and cotensored over (Def. ), then for fixed the operations of tensoring with and of cotensoring with form a pair of adjoint functors (Def. )
Proof
The hom-isomorphism (10) characterizing the pair of adjoint functors is provided by the composition of the natural isomorphisms (61) and (62):
Proposition
(in tensored and cotensored categories initial/terminal objects are enriched initial/terminal)
For a cosmos (Def. ) let be a -enriched category (Def. ).
If is both tensored and cotensored over (Def. ) then
-
an initial object (Def. ) of the underlying category of (Example ) is also enriched initial, in that the hom-object out of it is the terminal object of
-
a terminal object (Def. ) of the underlying category of (Example ) is also enriched terminal, in that the hom-object into it is the terminal object of :
Proof
We discuss the first claim, the second is formally dual.
By prop. , tensoring is a left adjoint. Since left adjoints preserve colimits (Prop. ), and since an initial object is the colimit over the empty diagram (Example ), it follows that
for all , in particular for . Therefore the natural isomorphism (62) implies for all that
where in the last step we used that the internal hom in sends colimits in its first argument to limits (Prop. ) and used that a terminal object is the limit over the empty diagram (Example ).
Kan extensions
Proposition
For a cosmos (Def. ), let be small -enriched categories (Def. ) and let
be a -enriched functor (Def. ). Then precomposition with constitutes a functor between the corresponding -enriched presheaf categories (Def. )
-
This enriched functor (63) has an enriched left adjoint (Def. ), called left Kan extension along
which is given objectwise by the coend (def. ):
(64) -
The enriched functor (63) has an enriched right adjoint (Def. ), called right Kan extension along
which is given objectwise by the end (def. ):
(65)
In summary, this means that the enriched functor
induces, via Kan extension, an adjoint triple (Remark ) of enriched functors
Proof
Use the expression of enriched natural transformations in terms of coends (example and def. ), then use the respect of for ends/coends (remark ), use the internal-hom adjunction (38), use the Fubini theorem (prop. ) and finally use Yoneda reduction (prop. ) to obtain a sequence of natural isomorphisms as follows:
and similarly:
Example
(coend formula for left Kan extension of ordinary presheaves)
Consider the cosmos to be Set, via Example , so that small -enriched categories (Def. ) are just a plain small category (Def. ) by Example , and -enriched presheaves (Example ) are just plain presheaves (Example ).
Then for any plain functor (Def. )
the general formula (64) for left Kan extension
is
Using here the Yoneda lemma (Prop. ) to rewrite , this is
Hence this coend-set consists of equivalence classes of pairs of morphisms
where two such are regarded as equivalent whenever there is such that
This is particularly suggestive when is a full subcategory inclusion (Def. ). For in that case we may imagine that a representative pair is a stand-in for the actual pullback of elements of along the would-be composite “”, only that this composite need not be defined. But the above equivalence relation is precisely that under which this composite would be invariant.
Further properties
We collect here further key properties of the various universal constructions considered above.
Proposition
(left Kan extension preserves representable functors)
For a cosmos (Def. ), let
be a -enriched functor (Def. ) between small -enriched categories (Def. ).
Then the left Kan extension (Prop. ) takes representable enriched presheaves to their image under :
for all .
Proof
By the coend formula (64) we have, naturally in , the expression
where the last step is the co-Yoneda lemma (Prop. ).
Example
(Kan extension of adjoint pair is adjoint quadruple)
For a cosmos (Def. ), let , be two small -enriched categories (Def. ) and let
be a -enriched adjunction (Def. ). Then there are -enriched natural isomorphisms (Def. )
between the precomposition on enriched presheaves with one functor and the left/right Kan extension of the other (Def. ).
By essential uniqueness of adjoint functors, this means that the two adjoint triples (Remark ) given by Kan extension (66) of and
merge into an adjoint quadruple (Remark )
Proof
For every enriched presheaf we have a sequence of -enriched natural isomorphism as follows
Here the first step is the coend-formula for left Kan extension (Prop. ), the second step if the enriched adjunction-isomorphism (47) for and the third step is the co-Yoneda lemma.
This shows the first statement, which, by essential uniqueness of adjoints, implies the following statements.
Proposition
(left Kan extension along fully faithful functor is fully faithful)
For a cosmos (Def. ), let
be a fully faithful -enriched functor (Def. ) between small -enriched categories (Def. ).
Then for all
and in fact the -unit of an adjunction is a natural isomorphism
is a fully faithful functor.
Proof
By the coend formula (64) we have, naturally in , the left Kan extension of any on the image of is
where in the second step we used the assumption of fully faithfulness of and in the last step we used the co-Yoneda lemma (Prop. ).
Lemma
(colimit of representable is singleton)
Let be a small category (Def. ). Then the colimit of a representable presheaf (Def. ), regarded as a functor
Proof
One way to see this is to regard the colimit as the left Kan extension (Prop. ) along the unique functor to the terminal category (Def. ). By the formula (64) this is
where we made explicit the constant functor , constant on the singleton set , and then applied the co-Yoneda lemma (Prop. ).
Proposition
(categories with finite products are cosifted
Let be a small category (Def. ) which has finite products. Then is a cosifted category, equivalently its opposite category is a sifted category, equivalently colimits over with values in Set are sifted colimits, equivalently colimits over with values in Set commute with finite products, as follows:
For to functors on the opposite category of (hence two presheaves on , Example ) we have a natural isomorphism (Def. )
between the colimit of their Cartesian product and the Cartesian product of their separate colimits.
Proof
First observe that for two presheaves, their Cartesian product is a colimit over presheaves represented by Cartesian products in . Explicity, using coend-notation, we have:
where denotes the Yoneda embedding.
This is due to the following sequence of natural isomorphisms:
where the first step expands out both presheaves as colimits of representables separately, via the co-Yoneda lemma (Prop. ), the second step uses that the Cartesian product of presheaves is a two-variable left adjoint (by the symmetric closed monoidal structure on presheaves) and as such preserves colimits (in particular coends) in each variable separately (Prop. ), and under the brace we use the defining universal property of the Cartesian products, assumed to exist in .
With this, we have the following sequence of natural isomorphisms:
Here the first step is (68), the second uses that colimits commute with colimits (Prop. ), the third uses again that the Cartesian product respects colimits in each variable separately, the fourth is by Lemma , the last step is again the respect for colimits of the Cartesian product in each variable separately.
Basic notions of Topos theory
We have explained in Remark how presheaves on a category may be thought of as generalized spaces probe-able by the objects of , and that two consistency conditions on this interpretation are provided by the Yoneda lemma (Prop. ) and the resulting Yoneda embedding (Prop. ). Here we turn to a third consistency condition that one will want to impose, namely a locality or gluing condition (Remark below), to be called the sheaf condition (Def. below).
More in detail, we had seen that any category of presheaves is the free cocompletion of the given small category (Prop. ) and hence exhibits generalized spaces as being glued or generated form the “ordinary spaces” . Further conditions to be imposed now will impose relations among these generators, such as the locality relation embodied by the sheaf-condition.
It turns out that these relations are reflected by special properties of an adjunction (Def. ) that relates generalized spaces to ordinary spaces:
generalized spaces via generators and relations:
| free cocompletion presheaves | loc. presentable category | sheaf topos |
|---|---|---|
| Prop. | Def. | Prop. |
| simplicial presheaves | combinatorial model category | model topos |
| Example | Def. | Def. |
Remark
(sheaf condition as local-to-global principle for generalized spaces)
If the objects of are thought of as spaces of sorts, as in Remark , then there is typically a notion of locality in these spaces, reflected by a notion of what it means to cover a given space by (“smaller”) spaces (a coverage, Def. below).
But if a space is covered, say by two other spaces , via morphisms
then this must be reflected in the behaviour of the probes of any generalized space (in the sense of Remark ) by these test spaces:
For ease of discussion, suppose that there is a sense in which these two patches above intersect in to form a space . Then locality of probes should imply that the ways of mapping and into such that these maps agree on the intersection , should be equivalent to the ways of mapping all of into .
One could call this the condition of locality of probes of generalized spaces probeable by objects of . But the established terminology is that this is the sheaf condition (74) on presheaves over . Those presheaves which satisfy this condition are called the sheaves (Def. below).
Remark
Warning
Most (if not all) introductions to sheaf theory insist on motivating the concept from the special case of sheaves on topological spaces (Example below). This is good motivation for what Grothendieck called “petit topos”-theory. The motivation above, instead, naturally leads to the “gros topos”-perspective, as in Example below, which is more useful for discussing the synthetic higher supergeometry of physics. In fact, this is the perspective of functorial geometry that has been highlighted since Grothendieck 65, but which has maybe remained underappreciated.
We now first introduce the sheaf-condition (Def. ) below in its traditional form via “matching families” (Def. below). Then we show (Prop. below) how this is equivalently expressed in terms of Cech groupoids (Example below). This second formulation is convenient for understanding and handling various constructions in ordinary topos theory (for instance the definition of cohesive sites) and it makes immediate the generalization to higher topos theory.
Descent
Here we introduce the sheaf-condition (Def. below) in its component-description via matching families (Def. below). Then we consider some of the general key properties of the resulting categories of sheaves, such as notably their “convenience”, in the technical sense of Prop. below.
Definition
Let be a small category (Def. ). Then a coverage on is
-
for each object a set of indexed sets of morphisms into
called the coverings of ,
such that
-
for every covering of and every morphism there exists a refining covering of , meaning that for each there exists and a morphism such that
(69)
A small category equipped with a coverage is called a site.
Example
(canonical coverage on topological spaces)
The category Top of (small) topological spaces (Example ) carries a coverage (Def. ) whose coverings are the usal open covers of topological spaces.
The condition (69) on a coverage is met, since the preimages of open subsets under a continuous function are again open subsets, so that the preimages of an open cover consistitute an open cover of the domain, such that the commuting diagram-condition (69) is immediage.
Similarly, for a fixed topological space, there is the site whose underlying category is the category of opens of , which is the thin category (Example ) of open subsets of and subset inclusions, and whose coverings are again the open covers.
Example
(differentiably good open covers of smooth manifolds)
The category SmthMfd of smooth manifold (Example ) carries a coverage (Def. ), where for any smooth manifold of dimension , its coverings are collections of smooth functions from the Cartesian space to whose image is the inclusion of an open ball.
Hence these are the usual open covers of , but with the extra condition that every patch is diffeomorphic to a Cartesian space (hence to a smooth open ball).
One may further constrain this and ask that also all the non-empty finite intersections of these open balls are diffeomorphic to open balls. These are the differentiably good open covers.
To see that these coverings satisfy the condition (69): The plain pullback of an open cover along any continuous function is again an open cover, just not necessarily by patches diffeomorphic to open balls. But every open cover may be refined by one that is (see at good open cover), and this is sufficient for (69).
Example is further developed in the chapters smooth sets and on smooth homotopy types.
Definition
(matching family – descent object)
Let be a small category equipped with a coverage, hence a site (Def. ) and consider a presheaf (Example ) over .
Given an object and a covering of it (Def. ) we say that a matching family (of probes of ) is a tuple such that for all and pairs of morphisms satisfying
we have
We write
for the set of matching families for the given presheaf and covering.
This is also called the descent object of for descent along the covering .
Example
(matching families that glue)
Let be a small category equipped with a coverage, hence a site (Def. ) and consider a presheaf (Example ) over .
Given an object and a covering of it (Def. ), then every element
induces a matching family (Def. ) by
(That this indeed satisfies the matching condition follows immediately by the functoriality of .)
This construction provides a function of the form
The matching families in the image of this function are hence those tuples of probes of by the patches of which glue to a global probe out of .
Definition
(sheaves and sheaf toposes)
Let be a small category equipped with a coverage, hence a site (Def. ) and consider a presheaf (Example ) over .
The presheaf is called a sheaf if for every object and every covering of all matching families glue uniquely, hence if the comparison morphism (73) is a bijection
The full subcategory (Example ) of the category of presheaves over a given site , on those that are sheaves is the category of sheaves, denoted
A category which is equivalent (Def. ) to a category of sheaves is called a sheaf topos, or often just topos, for short.
For and two such sheaf toposes, a homomorphism between them, called a geometric morphism is an adjoint pair of functors (Def. )
such that
- the left adjoint , called the inverse image, preserves finite products.
Hence there is a category Topos, whose objects are sheaf toposes and whose morphisms are geometric morphisms.
Example
(global sections geometric morphism)
Let be a sheaf topos (Def. ). Then there is a geometric morphism (76) to the category of sets (Example ), unique up to natural isomorphism (Def. ):
Here is called the global sections-functor.
Proof
Notice that every set is the coproduct, indexed by itself, of the terminal object (the singleton):
Since is a left adjoint, it preserves this coproduct (Prop. ). Moreover, since is assumed to preserve finite products, and since the terminal object is the empty product (Example ), it also preserves the terminal object. Therefore is fixed, up to natural isomorphism, to act as
This shows that exists and uniquely so, up to natural isomorphism. This implies the essential uniqueness of by uniqueness of adjoints (Prop. ).
Example
For a small category (Def. ), the trivial coverage on it is the coverage (Def. ) with no covering families at all, meaning that the sheaf condition (Def. ) over the resulting site is empty, in that every presheaf is a sheaf for this coverage.
Hence the category of presheaves (Example ) over a site with trivial coverage is already the corresponding category of sheaves, hence the corresponding sheaf topos:
Example
(sheaves on the terminal category are plain sets)
Consider the terminal category (Example ) equipped with its trivial coverage (Example ). Then there is a canonical equivalence of categories (Def. ) between the category of sheaves on this site (Def. ) and the category of sets (Example ):
Hence the category of sets is a sheaf topos.
Example
(sheaves on a topological space – spatial petit toposes)
In the literature, the concept of (pre-)sheaf (Def. ) is sometimes not defined relative to a site, but relative to a topological space. But the latter is a special case: For a topological space, consider its category of open subsets from Example , with coverage given by the usual open covers. Then a “sheaf on this topological space” is a sheaf, in the sense of Def. , on this site of opens. One writes
for short. The sheaf toposes arising this way are also called spatial toposes.
Proposition
The construction of categories of sheaves on a topological space (Example ) extends to a functor from the category Top of topological spaces and continuous functions between them (Example ) to the category Topos of sheaf toposes and geometric morphisms between them (Example ).
Moreover, when restricted to sober topological spaces, this becomes a fully faithful functor, hence a full subcategory-inclusion (Def. )
More generally, this holds for locales (i.e. for “sober topological spaces not necessarily supported on points”), in which case it becomes a reflective subcategory-inclusion (Def. )
This says that categories of sheaves on topological spaces are but a reflection of soper topological spaces (generally: locales) and nothing more, whence they are also called petit toposes.
Example
In the literature, sometimes sheaves are understood by default as taking values not in the category of sets, but in the category of abelian groups. Combined with Example this means that some authors really mean “sheaf of abelian groups of the site of opens of a topological space”, when they write just “sheaf”.
But for any mathematical structure, a sheaf of -structured sets is equivalently an -structure internal to the category of sheaves according to Def. . In particular sheaves of abelian groups are equivalently abelian group objects in the category of sheaves of sets as discussed here.
Example
Consider the site SmthMfd of all smooth manifolds, from Example . The category of sheaves over this (Def. ) is equivalent to the category of smooth sets, discussed in the chapter geometry of physics – smooth sets:
This is a gros topos, in a sense made precise by Def. below (a cohesive topos).
Remark
(ordinary spaces and their coverings are generators and relations for generalized spaces)
Given a site (Def. ), then its presheaf topos (Example ) is the free cocompletion of the category (Prop. ), hence the category obtained by freely forming colimits (“gluing”) of objects of .
In contrast, the full subcategory inclusion enforces relations between these free colimits.
Therefore in total we may think of a sheaf topos as obtained by generators and relations from the objects of its site :
-
the objects of are the generators;
-
the coverings of are the relations.
Proposition
(sheafification and plus construction)
Let be a site (Def. ). Then the full subcategory-inclusion (75) of the category of sheaves over (Def. ) into the category of presheaves (Example ) has a left adjoint (Def. ) called sheafification
An explicit formula for sheafification is given by applying the following “plus construction” twice:
Here the plus construction
is given by forming equivalence classes of sets of matching families (Def. ) for all possible covers (Def. )
under the equivalence relation which identifies two such pairs if the two covers have a joint refinement such that the restriction of the two matching families to that joint refinement coincide.
Example
Let be a site (Def. ). Then a full subcategory (Def. )
becomes a site itself, whose coverage consists of those coverings in that happen to be in .
Definition
Let and be sites (Def. ) with a a full subcategory-inclusion (Def. )
and regard as equipped with the induced coverage (Def. ).
This is called a dense subsite-inclusion if every object has a covering such that for all the patches are in the subcategory:
Proposition
Let be a dense subsite inclusion (def. ). Then precomposition with induces an equivalence of categories (Def. ) between their categories of sheaves (Def. ):
Proposition
(recognition of epi-/mono-/isomorphisms of sheaves)
Let be a site (Def. ) with its category of sheaves (Def. ).
Then a morphisms in is
-
a monomorphism (Def. ) or isomorphism (Def. ) precisely if it is so globally in that for each object in the site, then the component is an injection or bijection of sets, respectively.
-
an epimorphism (Def. ) precisely if it is so locally, in that: for all there is a covering such that for all and every element the element is in the image of .
Proposition
(epi/mono-factorization through image)
Let be a category of sheaves (Def. ). Then every morphism factors as an epimorphism followed by a monomorphism (Def. ) uniquely up to unique isomorphism:
Theobject , as a subobject of , is called the image of .
In fact this is an orthogonal factorization system, in that for every commuting square where the left morphism is an epimorphism, and the right one a monomorphism, there exists a unique lift:
This implies that this is a functorial factorization, in that for every commuting square
there is an induced morphism of images such that the resulting rectangular diagram commutes:
We discuss some of the key properties of sheaf toposes:
Proposition
(sheaf toposes are cosmoi)
Let be a site (Def. ) and its sheaf topos (Def. ). Then:
-
All limits exist in (Def. ), and they are computed as limits of presheaves, via Example :
-
All colimits exist in (Def. ) and they are given by the sheafification (Def. ) of the same colimits computed in the category of presheaves, via Example :
-
The cartesian (Example ) closed monoidal category-structure (Def. ) on the category of presheaves from Example restricts to sheaves:
In particular, for two sheaves, their internal hom is a sheaf given by
where is the presheaf represented by (Example ).
This may be summarized by saying that every sheaf topos (in particular every category of presheaves, by Example ) is a cosmos for enriched category theory (Def. ).
Definition
Let be a site (Def. ). Then a morphism of presheaves over (Example )
is called a local epimorphism if for every object , every morphism out of its represented presheaf (Example ) has the local lifting property through in that there is a covering (Def. ) and a commuting diagram of the form
Codescent
In order to understand the sheaf condition (74) better, it is useful to consider Cech groupoids (Def. below). These are really presheaves of groupoids (Def. below), a special case of the general concept of enriched presheaves. The key property of the Cech groupoid is that it co-represents the sheaf condition (Prop. below). It is in this incarnation that the concept of sheaf seamlessly generalizes to homotopy theory via “higher stacks”.
Definition
For a small category (Def. ) consider the functor category (Example ) from the opposite category of (Example ) to the category Grpd of small groupoids (Example )
By Example we may regard Grpd as a cosmos for enriched category theory. Since the inclusion (Example ) is a strong monoidal functor (Def. ) of cosmoi (Example ), the plain category may be thought of as a Grpd-enriched category (Def. ) and hence a functor is equivalently a Grpd-enriched functor (Def. ).
This means that the plain category of functors enriches to Grpd-enriched category of Grpd-enriched presheaves (Example ).
Hence we may speak of presheaves of groupoids.
Remark
(presheaves of groupoids as internal groupoids in presheaves)
From every presheaf of groupoids (Def. ), we obtain two ordinary presheaves of sets (Def. ) called the
-
presheaf of objects
-
the presheaf of morphisms
In more abstract language this assignment constitutes an equivalence of categories
from presheaves of groupoids to internal groupoids- in the category of presheaves over (Def. ).
Example
(presheaves of sets form reflective subcategory of presheaves of groupoids)
Let be a small category (Def. ). There is the reflective subcategory-inclusion (Def. ) of the category of presheaves over (Example ) into the category of presheaves of groupoids over (Def. )
which is given over each object of by the reflective inclusion of sets into groupoids (Example ).
Example
Let be a site (Def. ), and an object of that site. For each covering family of in the given coverage, the Cech groupoid is the presheaf of groupoids (Def. )
which, regarded as an internal groupoid in the category of presheaves over , via (78), has as presheaf of objects the coproduct
of the presheaves represented (under the Yoneda embedding, Prop. ) by the covering objects , and as presheaf of morphisms the coproduct over all fiber products of these:
This means equivalently that for any the groupoid assigned by has as set of objects pairs consisting of an index and a morphism in , and there is a unique morphism between two such objects
precisely if
Condition (79) for morphisms in the Cech groupoid to be well-defined is verbatim the condition (70) in the definition of matching families. Indeed, Cech groupoids serve to conveniently summarize (and then generalize) the sheaf condition (Def. ):
Proposition
(Cech groupoid co-represents matching families – codescent)
For Grpd regarded as a cosmos (Example ), and a site (Def. ), let
be a presheaf on (Example ), regarded as a Grpd-enriched presheaf via Example , let be any object and a covering family (Def. ) with induced Cech groupoid (Example ).
Then there is an isomorphism
between the hom-groupoid of Grpd-enriched presheaves (Def. ) and the set of matching families (Def. ).
Since hence the Cech-groupoid co-represents the descent object, it is sometimes called the codescent object along the given covering.
Moreover, under this identification the canonical morphism
induces the comparison morphism (73)
In conclusion, this means that the presheaf is a sheaf (Def. ) precisely if homming Cech groupoid projections into it produces an isomorphism:
One also says in this case that is a local object with respect to Cech covers/
Proof
By (58) the hom-groupoid is computed as the end
where, by Example , the “integrand” is the functor category (here: a groupoid) from the Cech groupoid at a given to the set (regarded as a groupoid) assigned by to .
Since is just a set, that functor groupoid, too, is just a set, regarded as a groupoid. Its elements are the functors , which are equivalently those functions on sets of objects
which respect the equivalence relation induced by the morphisms in the Cech groupoid at .
Hence the hom-groupoid is a subset of the end of these function sets:
Here we used: first that the internal hom-functor turns colimits in its first argument into limits (Prop. ), then that limits commute with limits (Prop. ), hence that in particular ends commute with products , and finally the enriched Yoneda lemma (Prop. ), which here is, via Example , just the plain Yoneda lemma (Prop. ). The end result is hence the same Cartesian product set that also the set of matching families is defined to be a subset of, in (72).
This shows that an element in is a tuple , subject to some condition. This condition is that for each the assignment
constitutes a functor of groupoids.
By definition of the Cech groupoid, and since the codomain is a just set regarded as a groupoid, this is the case precisely if
which is exactly the condition (71) that makes a matching family.
Local presentation
We now discuss a more abstract characterization of sheaf toposes, in terms of properties enjoyed by the adjunction that relates them to the corresponding categories of presheaves.
Definition
(locally presentable category)
A category (Def. ) is called locally presentable if there exists a small category (Def. ) and a reflective subcategory-inclusion of into its category of presheaves (Example )
such that the inclusion functor is an accessible functor in that it preserves -filtered colimits for some regular cardinal .
Proposition
A sheaf topos (Def. ) is equivalently a locally presentable category (Def. ) with
Proposition
(sheaf toposes are equivalently the left exact reflective subcategories of presheaf toposes)
Let be a site (Def. ). Then the full subcategory inclusion of its sheaf topos (Def. ) into its category of presheaves is a reflective subcategory inclusion (Def. )
such that:
-
the inclusion is an accessible functor, thus exhibiting as a locally presentable category (Def. )
-
the reflector (which is sheafification, Prop. ) is left exact (“lex”) in that it preserves finite limits.
Conversely, every sheaf topos arises this way. Hence sheaf toposes are equivalently the left exact-reflectively full subcategories of presheaf toposes over some small category :
(e.g. Borceux 94, prop. 3.5.4, cor. 3.5.5, Johnstone, C.2.1.11)
Remark
(left exact reflections of categories of presheaves are locally presentable categories)
In the characterization of sheaf toposes as left exact reflections of categories of presheaves in Prop. , the accessibility of the inclusion, equivalently the local presentability (Def. ) is automatically implied (using the adjoint functor theorem), as indicated in (82).
Gros toposes
We have seen roughly two different kinds of sheaf toposes:
-
categories of sheaves on a given space (Example ), which, by localic reflection (Prop. ), really are just a reflection of the space in the category of toposes,
these are called petit toposes;
-
categories of sheaves whose objects are generalized spaces (Example )
these are called gros toposes.
Remark
(cohesive generalized spaces as foundations of geometry)
If we aim to lay foundations for geometry, then we are interested in isolating those kinds of generalized spaces which have foundational a priori meaning, independent of an otherwise pre-configured notion of space. Hence we would like to first characterize suitable gros toposes, extract concepts of space from these, and only then, possibly, consider the petit topos-reflections of these (Prop. below).
The gros toposes of such foundational generalized spaces ought to have an internal logic that knows about modalities of geometry such as discreteness or concreteness. Via the formalization of modalities in Def. this leads to the definiton of cohesive toposes (Def. , Prop. below, due to Lawvere 91, Lawvere 07).
| gros topos | generalized spaces obey… | example: | |
|---|---|---|---|
| cohesion | Def. | principles of differential topology | SmoothSet |
| elasticity | Def. | principles of differential geometry | FormallSmoothset |
| solidity | Def. | principles of supergeometry | SuperFormalSmoothSet |
Cohesive toposes
Definition
A sheaf topos (Def. ) is called a cohesive topos if there is a quadruple (Remark ) of adjoint functors (Def. ) to the category of sets (Example )
such that:
-
and are full and faithful functors (Def. )
Example
(adjoint quadruple of presheaves over site with finite products)
Let be a small category (Def. ) with finite products (hence with a terminal object and for any two objects their Cartesian product ).
Then there is an adjoint quadruple (Remark ) of functors between the category of presheaves over (Example ), and the category of sets (Example )
such that:
-
the functor sends a presheaf to its set of global sections, which here is its value on the terminal object:
(85) -
and are full and faithful functors (Def. ).
-
preserves finite products:
for , we have a natural bijection
Hence the category of presheaves over a small category with finite products, hence the category of sheaves for the trivial coverage (Example ) is a cohesive topos (Def. ).
Proof
The existence of the terminal object in means equivalently (by Example ) that there is an adjoint pair of functors between and the terminal category (Example ):
whose right adjoint takes the unique object of the terminal category to that terminal object.
From this it follows, by Example , that Kan extension produces an adjoint quadruple (Remark ) of functors between the category of presheaves and , as shown, where
-
is the operation of pre-composition with the terminal object inclusion
-
is the left Kan extension along the inclusion of the terminal object.
The former is manifestly the operation of evaluating on the terminal object. Moreover, since the terminal object inclusion is manifestly a fully faithful functor (Def. ), it follows that also its left Kan extension is fully faithful (Prop. ). This implies that also is fully faithful, by (Prop. ).
Equivalently, is the constant diagram-assigning functor. By uniqueness of adjoints (Prop. ) implies that is the functor that sends a presheaf, regarded as a functor , to its colimit
The fact that this indeed preserves products follows from the assumption that has finite products, since categories with finite products are cosifted (Prop. )
Example suggests to ask for coverages on categories with finite products which are such that the adjoint quadruple (107) on the category of presheaves (co-)restricts to the corresponding category of sheaves. The following Definition states a sufficient condition for this to be the case:
Definition
We call a site (Def. ) cohesive if the following conditions are satisfied:
-
The category has finite products (as in Example ).
-
For every covering family in the given coverage on the induced Cech groupoid (Def. ) satisfies the following two conditions:
-
the set of connected components of the groupoid obtained as the colimit over the Cech groupoid is the singleton:
-
the set of connected components of the groupoid obtained as the limit of the Cech groupoid is equivalent to the set of points of , regarded as a groupoid:
-
This definition is designed to make the following true:
Proposition
(category of sheaves on a cohesive site is a cohesive topos)
Let be a cohesive site (Def. ). Then the adjoint quadruple on the category of presheaves over , from Example (given that a cohesive site by definition has finite products) (co-)restricts from the category of presheaves over , to the category of sheaves (Def. ) and hence exhibits as a cohesive topos (Def. ):
Proof
By example we alreaday have the analogous statement for the categories of presheaves. Hence it is sufficient to show that the functors and from Example factor through the definition inclusion of the category of sheaves, hence that for each set the presheaves and are indeed sheaves (Def. ).
By the formulaton of the sheaf condition via the Cech groupoid (Prop. ), and using the adjunction hom-isomorphisms (here) this is readily seen to be equivalent to the two further conditions on a cohesive site (Def. ):
Let be a covering family.
The sheaf condition (81) for says that
is an isomorphism of groupoids, which by adjunction and using (86) means equivalently that
is an isomorphism of groupoids, where we used that colimits of representables are singletons (Lemma ) to replace .
But now in this internal hom of groupoids, the set is really a groupoid in the image of the reflective embedding of sets into groupoids, whose left adjoint is the connected components-functor (Example ). Hence by another adjunction isomoprhism this is equivalent to
being an isomorphism (a bijection of sets, now). This is true for all precisely if (by the Yoneda lemma, if you wish) the morphism
is already an isomorphism (here: bijection) itself.
Similarly, the sheaf condition (81) for says that
is an isomorphism, and hence by adjunction and using (85), this is equivalent to
being an isomorphism. This holds for all if (by the Yoneda lemma, if you wish)
is an isomorphism.
Definition
(adjoint triple of adjoint modal operators on cohesive topos)
Given a cohesive topos (Def. ), its adjoint quadruple (Remark ) of functors to and from Set
induce, by composition of functors, an adjoint triple (Remark ) of adjoint modalities (Def. ):
Since and are fully faithful functors by assumption, these are (co-)modal operators (Def. ) on the cohesive topos, by (Prop. ).
We pronounce these as follows:
| shape modality | flat modality | sharp modality |
|---|---|---|
and we refer to the corresponding modal objects (Def. ) as follows:
-
is called a discrete object;
-
is called a codiscrete object;
-
is a concrete object.
Proposition
(pieces have points discrete objects are concrete Aufhebung of bottom adjoint modality)
Let be a cohesive topos (Def. ). Then the following conditions are equivalent:
-
pieces have points: For every object , comparison of extremes-transformation (27) for the -adjoint modality (27), hence the -counit of an adjunction composed with the ʃ-unit
is an epimorphism (Def. )
-
discrete objects are concrete: For every object , we have that its discrete object is a concrete object (Def. ).
-
Aufhebung of bottom adjoint modality
The adjoint modality exhibits Aufhebung (Def. ) of the bottom adjoint modality (Example ), i.e. the initial object (Def. ) is codiscrete (Def. ):
Proof
The comparison morphism is a special case of that discussed in Prop. . First observe, in the notation there, that
In one direction, assume that is an epimorphism. By (31) we have , but is a left adjoint and left adjoints preserve monomorphisms (Prop. ).
In the other direction, assume that is an epimorphism. By (29) and (32) we see that is re-obtained from this by applying and then composition with isomorphisms. But is again a left adjoint, and hence preserves epimorphism by Prop. , as does composition with isomorphisms.
By applying (29) again, we find in particular that pieces have points is also equivalent to being an epimorphism, for all . But this is equivalent to
being a monomorphism for all (by adjunction isomorphism (10) and definition of epimorphism, Def. ).
Now by Lemma , this is equivalent to
being an injection for all , which, by Def. , is equivalent to being a monomorphism, hence to discrete objects are concrete.
This establishes the equivalence between the first two items.
Proposition
(cohesive site such that pieces have points/discrete objects are concrete)
Let be a cohesive site (Def. ), such that
- for every object , there is at least one morphism from the terminal object to , hence such that the hom set is non-empty.
Then the cohesive topos , according to Prop. , satisfies the equivalent conditions from Prop. :
Proof
By Prop. it is sufficient to show the second condition, hence to check that for each set , the canonical morphism
is a monomorphism. By Prop. this means equivalently that for each object in the site, the component function
is an injective function.
Now, by the proof of Prop. , this is the diagonal function
This function is injective precisely if is non-empty, which is true by assumption.
Proposition
(quasitopos of concrete objects in a cohesive topos)
For a cohesive topos (Def. ), write
for its full subcategory (Example ) of concrete objects (Def. ).
Then there is a sequence of reflective subcategory-inclusions (Def. ) that factor the -adjunction as
If in addition discrete objects are concrete (Prop. ), then the full adjoint quadruple factors through the concrete objects:
Proof
For the adjunction on the right, we just need to observe that for every set , the codiscrete object is concrete, which is immediate by idempotency of (Prop. ) and the fact that every isomorphism is also a monomorphism. Similarly, the assumption that discrete objects are concrete says exactly that also factors through .
For the adjunction on the left we claim that the left adjoint , (to be called concretification), is given by sending each object to the image (Def. ) of its adjunction unit :
hence to the object which exhibits the epi/mono-factorization (Prop. ) of
First we need to show that , thus defined, is indeed concrete, hence that is a monomorphism (Def. ). For this, consider the following naturality square (11) of the -adjunction hom-isomorphism
By chasing the identity morphism on through this diagram, as shown by the diagram on the right, we obtain the equality displayed in the bottom right entry, where we used the general formula for adjuncts (Prop. ) and the definition (Def. ).
But observe that , and hence also , is an isomorphism (Def. ), as indicated above: Since is both a left adjoint as well as a right adjoint, it preserves both epimorphisms as well as monomorphisms (Prop. ), hence it preserves image factorizations (Prop. ). This implies that is the epimorphism onto the image of . But by idempotency of , the latter is an isomorphism, and hence so is the epimorphism in its image factorization.
Therefore the equality in (90) says that
where in the second line we remembered that is, by definition, the epimorphism in the epi/mono-factorization of .
Now the defining property of epimorphisms (Def. ) allows to cancel this commmon factor on both sides, which yields
This shows that is indeed concret.
It remains to show that this construction is left adjoint to the inclusion. We claim that the adjunction unit (Def. ) of is provided by (89).
To see this, first notice that, since the epi/mono-factorization (Prop. ) is orthogonal and hence functorial, we have commuting diagrams of the form
Now to demonstrate the adjunction it is sufficient, by Prop. , to show that is a universal morphism in the sense of Def. . Hence consider any morphism with . Then we need to show that there is a unique diagonal morphism as below, that makes the following top left triangle commute:
Now, from (91), we have a commuting square as shown. Here the left morphism is an epimorphism by construction, while the right morphism is a monomorphism by assumption on . With this, the epi/mono-factorization in Prop. says that there is a diagonal lift which makes both triangles commute.
It remains to see that the lift is unique with just the property of making the top left triangle commute. But this is equivalently the statement that the left morphism is an epimorphism, by Def. .
The equivalence of the first two follows with (Johnstone, lemma 2.1, corollary 2.2). The equivalence of the first and the last is due to Lawvere-Menni 15, lemma 4.1, lemma 4.2.
Elastic toposes
Definition
Let be a cohesive topos (Def. ). Then an elastic topos or differentially cohesive topos over is a sheaf topos which is
-
a cohesive topos over Set,
-
equipped with a quadruple of adjoint functors (Def. ) to of the form
Lemma
(progression of (co-)reflective subcategories of elastic topos)
Let be an elastic topos (Def. ) over a cohesive topos (Def. ):
and write
for the adjoint quadruple exhibiting the cohesion of itself. Then these adjoint functors arrange and decompose as in the following diagram

Proof
The identification
follows from the essential uniqueness of the global section-geometric morphism (Example ). This implies the identifications by essential uniqueness of adjoints (Prop. ).
Definition
(adjoint modalities on elastic topos)
Given an elastic topos (differentially cohesive topos) over (Def. ), composition of the functors in Lemma yields, via Prop. , the following adjoint modalities (Def. )
Since and are fully faithful functors by assumption, these are (co-)modal operators (Def. ) on the cohesive topos, by (Prop. ).
We pronounce these as follows:
| reduction modality | infinitesimal shape modality | infinitesimal flat modality |
|---|---|---|
and we refer to the corresponding modal objects (Def. ) as follows:
-
is called a reduced object;
-
an infinitesimal shape-modal object
is called a coreduced object.
Proposition
(progression of adjoint modalities on elastic topos)
Let be an elastic topos (Def. ) and consider the corresponding adjoint modalities which it inherits
-
for being a cohesive topos, from Def. ,
-
for being an elastic topos, from Def. :
| shape modality | flat modality | sharp modality |
|---|---|---|
| reduction modality | infinitesimal shape modality | infinitesimal flat modality |
Then these arrange into the following progression, via the preorder on modalities from Def.
where we display also the bottom adjoint modality (Example ), for completeness.
Proof
We need to show, for all , that
-
is an -modal object (Def. ), hence that
-
is an -modal object (Def. ), hence that
After unwinding the definitions of the modal operators Def. and Def. , and using their re-identification from Lemma , this comes down to the fact that
which holds by Prop. , since is a fully faithful functor and , are (co-)reflectors for it, respectively:
and
Solid toposes
Definition
Let be an elastic topos (Def. ) over a cohesive topos (Def. ). Then a solid topos or super-differentially cohesive topos over is a sheaf topos , which is
-
a cohesive topos over Set (Def. ),
-
an elastic topos over ,
-
equipped with a quadruple of adjoint functors (Def. ) to of the form
hence with and being fully faithful functors (Def. ).
Lemma
(progression of (co-)reflective subcategories of solid topos)
Let be a solid topos (Def. ) over an elastic topos (Def. ):
Then these adjoint functors arrange and decompose as shown in the following diagram:
Here the composite adjoint quadruple
exhibits the cohesion of over Set, and the composite adjoint quadruple
exhibits the elasticity of over .
Proof
As in the proof of Prop. , this is immediate by the essential uniqueness of adjoints (Prop. ) and of the global section-geometric morphism (Example ).
Definition
(adjoint modalities on solid topos)
Given a solid topos over (Def. ), composition of the functors in Lemma yields, via Prop. , the following adjoint modalities (Def. )
Since and are fully faithful functors by assumption, these are (co-)modal operators (Def. ) on the cohesive topos, by (Prop. ).
We pronounce these as follows:
| fermionic modality | bosonic modality | rheonomy modality |
|---|---|---|
and we refer to the corresponding modal objects (Def. ) as follows:
-
is called a bosonic object;
-
a -modal object
is called a rheonomic object;
Proposition
(progression of adjoint modalities on solid topos)
Let be a solid topos (Def. ) and consider the adjoint modalities which it inherits
-
for being a cohesive topos, from Def. ,
-
for being an elastic topos, from Def. ,
-
for being a solid topos, from Def. :
| shape modality | flat modality | sharp modality |
|---|---|---|
| reduction modality | infinitesimal shape modality | infinitesimal flat modality |
| fermionic modality | bosonic modality | rheonomy modality |
Then these arrange into the following progression, via the preorder on modalities from Def. :
where we are displaying, for completeness, also the adjoint modalities at the bottom and the top (Example ).
Proof
By Prop. , it just remains to show that for all objects
-
is an -modal object, hence ,
-
is a bosonic object, hence .
The proof is directly analogous to that of Prop. , now using the decompositions from Lemma :
and
(…)
Basic notions of homotopy theory
Traditionally, mathematics and physics have been founded on set theory, whose concept of sets is that of “bags of distinguishable points”.
But fundamental physics is governed by the gauge principle. This says that given any two “things”, such as two field histories and , it is in general wrong to ask whether they are equal or not, instead one has to ask where there is a gauge transformation
between them. In mathematics this is called a homotopy.
This principle applies also to gauge transformations/homotopies themselves, and thus leads to gauge-of-gauge transformations or homotopies of homotopies
and so on to ever higher gauge transformations or higher homotopies:
This shows that what an here are elements of is not really a set in the sense of set theory. Instead, such a collection of elements with higher gauge transformations/higher homotopies between them is called a homotopy type.
Hence the theory of homotopy types – homotopy theory – is much like set theory, but with the concept of gauge transformation/homotopy built right into its foundations. Homotopy theory is gauged mathematics.
A classical model for homotopy types are simply topological spaces: Their points represent the elements, the continuous paths between points represent the gauge transformations, and continuous deformations of paths represent higher gauge transformations. A central result of homotopy theory is the proof of the homotopy hypothesis, which says that under this identification homotopy types are equivalent to topological spaces viewed, in turn, up to “weak homotopy equivalence”.
In the special case of a homotopy type with a single element , the gauge transformations necessarily go from to itself and hence form a group of symmetries of .
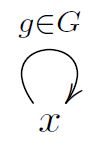
This way homotopy theory subsumes group theory.
If there are higher order gauge-of-gauge transformations/homotopies of homotopies between these symmetry group-elements, then one speaks of 2-groups, 3-groups, … n-groups, and eventually of ∞-groups. When homotopy types are represented by topological spaces, then ∞-groups are represented by topological groups.
This way homotopy theory subsumes parts of topological group theory.
Since, generally, there is more than one element in a homotopy type, these are like “groups with several elements”, and as such they are called groupoids (Def. ).
If there are higher order gauge-of-gauge transformations/homotopies of homotopies between the transformations in such a groupoid, one speaks of 2-groupoids, 3-groupoids, … n-groupoids, and eventually of ∞-groupoids. The plain sets are recovered as the special case of 0-groupoids.
Due to the higher orders appearing here, mathematical structures based not on sets but on homotopy types are also called higher structures.
Hence homotopy types are equivalently ∞-groupoids. This perspective makes explicit that homotopy types are the unification of plain sets with the concept of gauge-symmetry groups.
An efficient way of handling ∞-groupoids is in their explicit guise as Kan complexes (Def. below); these are the non-abelian generalization of the chain complexes used in homological algebra. Indeed, chain homotopy is a special case of the general concept of homotopy, and hence homological algebra forms but a special abelian corner within homotopy theory. Conversely, homotopy theory may be understood as the non-abelian generalization of homological algebra.
Hence, in a self-reflective manner, there are many different but equivalent incarnations of homotopy theory. Below we discuss in turn:
-
∞-groupoids modeled by topological spaces. This is the classical model of homotopy theory familiar from traditional point-set topology, such as covering space-theory.
-
∞-groupoids modeled on simplicial sets, whose fibrant objects are the Kan complexes. This simplicial homotopy theory is Quillen equivalent to topological homotopy theory (the “homotopy hypothesis”), which makes explicit that homotopy theory is not really about topological spaces, but about the ∞-groupoids that these represent.
Ideally, abstract homotopy theory would simply be a complete replacement of set theory, obtained by removing the assumption of strict equality, relaxing it to gauge equivalence/homotopy. As such, abstract homotopy theory would be part and parcel of the foundations of mathematics themselves, not requiring any further discussion. This ideal perspective is the promise of homotopy type theory and may become full practical reality in the next decades.
Until then, abstract homotopy theory has to be formulated on top of the traditional foundations of mathematics provided by set theory, much like one may have to run a Linux emulator on a Windows machine, if one does happen to be stuck with the latter.
A very convenient and powerful such emulator for homotopy theory within set theory is model category theory, originally due to Quillen 67 and highly developed since. This we introduce here.
The idea is to consider ordinary categories (Def. ) but with the understanding that some of their morphisms
should be homotopy equivalences (Def. ), namely similar to isomorphisms (Def. ), but not necessarily satisfying the two equations defining an actual isomorphism
but intended to satisfy this only with equality relaxed to gauge transformation/homotopy:
Such would-be homotopy equivalences are called weak equivalences (Def. below).
In principle, this information already defines a homotopy theory by a construction called simplicial localization, which turns weak equivalences into actual homotopy equivalences in a suitable way.
However, without further tools this construction is unwieldy. The extra structure of a model category (Def. below) on top of a category with weak equivalences provides a set of tools.
The idea here is to abstract (in Def. below) from the evident concepts in topological homotopy theory of left homotopy (Def. ) and right homotopy (Def. ) between continuous functions: These are provided by continuous functions out of a cylinder space or into a path space , respectively, where in both cases the interval space serves to parameterize the relevant gauge transformation/homotopy.
Now a little reflection shows (this was the seminal insight of Quillen 67) that what really matters in this construction of homotopies is that the path space factors the diagonal morphism from a space to its Cartesian product as
while the cylinder serves to factor the codiagonal morphism as
where in both cases “fibration” means something like well behaved surjection, while “cofibration” means something like satisfying the lifting property (Def. below) against fibrations that are also weak equivalences.
Such factorizations subject to lifting properties is what the definition of model category axiomatizes, in some generality. That this indeed provides a good toolbox for handling homotopy equivalences is shown by the Whitehead theorem in model categories (Lemma below), which exhibits all weak equivalences as actual homotopy equivalences after passage to “good representatives” of objects (fibrant/cofibrant resolutions, Def. below). Accordingly, the first theorem of model category theory (Quillen 67, I.1 theorem 1, reproduced as Theorem below), provides a tractable expression for the hom-sets modulo homotopy equivalence of the underlying category with weak equivalences in terms of actual morphisms out of cofibrant resolutions into fibrant resolutions (Lemma below).
This is then generally how model category-theory serves as a model for homotopy theory: All homotopy-theoretic constructions, such as that of long homotopy fiber sequences (Prop. below), are reflected via constructions of ordinary category theory but applied to suitably resolved objects.
Literature (Dwyer-Spalinski 95)
Definition
A model category is
such that
-
the class makes into a category with weak equivalences, def. ;
-
The pairs and are both weak factorization systems, def. .
One says:
-
elements in are weak equivalences,
-
elements in are cofibrations,
-
elements in are fibrations,
-
elements in are acyclic cofibrations,
-
elements in are acyclic fibrations.
The form of def. is due to (Joyal, def. E.1.2). It implies various other conditions that (Quillen 67) demands explicitly, see prop. and prop. below.
We now dicuss the concept of weak factorization systems (Def. below) appearing in def. .
Factorization systems
Definition
Let be any category. Given a diagram in of the form
then an extension of the morphism along the morphism is a completion to a commuting diagram of the form
Dually, given a diagram of the form
then a lift of through is a completion to a commuting diagram of the form
Combining these cases: given a commuting square
then a lifting in the diagram is a completion to a commuting diagram of the form
Given a sub-class of morphisms , then
- a morphism as above is said to have the right lifting property against or to be a -injective morphism if in all square diagrams with on the right and any on the left a lift exists.
dually:
- a morphism is said to have the left lifting property against or to be a -projective morphism if in all square diagrams with on the left and any on the left a lift exists.
Definition
A weak factorization system (WFS) on a category is a pair of classes of morphisms of such that
-
Every morphism of may be factored as the composition of a morphism in followed by one in
-
The classes are closed under having the lifting property, def. , against each other:
-
is precisely the class of morphisms having the left lifting property against every morphisms in ;
-
is precisely the class of morphisms having the right lifting property against every morphisms in .
-
Definition
For a category, a functorial factorization of the morphisms in is a functor
which is a section of the composition functor .
Remark
In def. we are using the following standard notation, see at simplex category and at nerve of a category:
Write and for the ordinal numbers, regarded as posets and hence as categories. The arrow category is equivalently the functor category , while has as objects pairs of composable morphisms in . There are three injective functors , where omits the index in its image. By precomposition, this induces functors . Here
-
sends a pair of composable morphisms to their composition;
-
sends a pair of composable morphisms to the first morphisms;
-
sends a pair of composable morphisms to the second morphisms.
Definition
A weak factorization system, def. , is called a functorial weak factorization system if the factorization of morphisms may be chosen to be a functorial factorization , def. , i.e. such that lands in and in .
Remark
Not all weak factorization systems are functorial, def. , although most (including those produced by the small object argument (prop. below), with due care) are.
Proposition
Let be a category and let be a class of morphisms. Write and , respectively, for the sub-classes of -projective morphisms and of -injective morphisms, def. . Then:
-
Both classes contain the class of isomorphism of .
-
Both classes are closed under composition in .
is also closed under transfinite composition.
-
Both classes are closed under forming retracts in the arrow category (see remark ).
-
is closed under forming pushouts of morphisms in (“cobase change”).
is closed under forming pullback of morphisms in (“base change”).
-
is closed under forming coproducts in .
is closed under forming products in .
Proof
We go through each item in turn.
containing isomorphisms
Given a commuting square
with the left morphism an isomorphism, then a lift is given by using the inverse of this isomorphism . Hence in particular there is a lift when and so . The other case is formally dual.
closure under composition
Given a commuting square of the form
consider its pasting decomposition as
Now the bottom commuting square has a lift, by assumption. This yields another pasting decomposition
and now the top commuting square has a lift by assumption. This is now equivalently a lift in the total diagram, showing that has the right lifting property against and is hence in . The case of composing two morphisms in is formally dual. From this the closure of under transfinite composition follows since the latter is given by colimits of sequential composition and successive lifts against the underlying sequence as above constitutes a cocone, whence the extension of the lift to the colimit follows by its universal property.
closure under retracts
Let be the retract of an , i.e. let there be a commuting diagram of the form.
Then for
a commuting square, it is equivalent to its pasting composite with that retract diagram
Here the pasting composite of the two squares on the right has a lift, by assumption:
By composition, this is also a lift in the total outer rectangle, hence in the original square. Hence has the left lifting property against all and hence is in . The other case is formally dual.
closure under pushout and pullback
Let and and let
be a pullback diagram in . We need to show that has the right lifting property with respect to all . So let
be a commuting square. We need to construct a diagonal lift of that square. To that end, first consider the pasting composite with the pullback square from above to obtain the commuting diagram
By the right lifting property of , there is a diagonal lift of the total outer diagram
By the universal property of the pullback this gives rise to the lift in
In order for to qualify as the intended lift of the total diagram, it remains to show that
commutes. To do so we notice that we obtain two cones with tip :
-
one is given by the morphisms
with universal morphism into the pullback being
-
the other by
- .
with universal morphism into the pullback being
- .
The commutativity of the diagrams that we have established so far shows that the first and second morphisms here equal each other, respectively. By the fact that the universal morphism into a pullback diagram is unique this implies the required identity of morphisms.
The other case is formally dual.
closure under (co-)products
Let be a set of elements of . Since colimits in the presheaf category are computed componentwise, their coproduct in this arrow category is the universal morphism out of the coproduct of objects induced via its universal property by the set of morphisms :
Now let
be a commuting square. This is in particular a cocone under the coproduct of objects, hence by the universal property of the coproduct, this is equivalent to a set of commuting diagrams
By assumption, each of these has a lift . The collection of these lifts
is now itself a compatible cocone, and so once more by the universal property of the coproduct, this is equivalent to a lift in the original square
This shows that the coproduct of the has the left lifting property against all and is hence in . The other case is formally dual.
An immediate consequence of prop. is this:
Corollary
Let be a category with all small colimits, and let be a sub-class of its morphisms. Then every -injective morphism, def. , has the right lifting property, def. , against all -relative cell complexes, def. and their retracts, remark .
Remark
By a retract of a morphism in some category we mean a retract of as an object in the arrow category , hence a morphism such that in there is a factorization of the identity on through
This means equivalently that in there is a commuting diagram of the form
Lemma
In every category the class of isomorphisms is preserved under retracts in the sense of remark .
Proof
For
a retract diagram and an isomorphism, the inverse to is given by the composite
More generally:
Proposition
Given a model category in the sense of def. , then its class of weak equivalences is closed under forming retracts (in the arrow category, see remark ).
Proof
Let
be a commuting diagram in the given model category, with a weak equivalence. We need to show that then also .
First consider the case that .
In this case, factor as a cofibration followed by an acyclic fibration. Since and by two-out-of-three (def. ) this is even a factorization through an acyclic cofibration followed by an acyclic fibration. Hence we obtain a commuting diagram of the following form:
where is uniquely defined and where is any lift of the top middle vertical acyclic cofibration against . This now exhibits as a retract of an acyclic fibration. These are closed under retract by prop. .
Now consider the general case. Factor as an acyclic cofibration followed by a fibration and form the pushout in the top left square of the following diagram
where the other three squares are induced by the universal property of the pushout, as is the identification of the middle horizontal composite as the identity on . Since acyclic cofibrations are closed under forming pushouts by prop. , the top middle vertical morphism is now an acyclic fibration, and hence by assumption and by two-out-of-three so is the middle bottom vertical morphism.
Thus the previous case now gives that the bottom left vertical morphism is a weak equivalence, and hence the total left vertical composite is.
Lemma
Consider a composite morphism
-
If has the left lifting property against , then is a retract of .
-
If has the right lifting property against , then is a retract of .
Proof
We discuss the first statement, the second is formally dual.
Write the factorization of as a commuting square of the form
By the assumed lifting property of against there exists a diagonal filler making a commuting diagram of the form
By rearranging this diagram a little, it is equivalent to
Completing this to the right, this yields a diagram exhibiting the required retract according to remark :
Small object argument
Given a set of morphisms in some category , a natural question is how to factor any given morphism through a relative -cell complex, def. , followed by a -injective morphism, def.
A first approximation to such a factorization turns out to be given simply by forming by attaching all possible -cells to . Namely let
be the set of all ways to find a -cell attachment in , and consider the pushout of the coproduct of morphisms in over all these:
This gets already close to producing the intended factorization:
First of all the resulting map is a -relative cell complex, by construction.
Second, by the fact that the coproduct is over all commuting squres to , the morphism itself makes a commuting diagram
and hence the universal property of the colimit means that is indeed factored through that -cell complex ; we may suggestively arrange that factorizing diagram like so:
This shows that, finally, the colimiting co-cone map – the one that now appears diagonally – almost exhibits the desired right lifting of against the . The failure of that to hold on the nose is only the fact that a horizontal map in the middle of the above diagram is missing: the diagonal map obtained above lifts not all commuting diagrams of into , but only those where the top morphism factors through .
The idea of the small object argument now is to fix this only remaining problem by iterating the construction: next factor in the same way into
and so forth. Since relative -cell complexes are closed under composition, at stage the resulting is still a -cell complex, getting bigger and bigger. But accordingly, the failure of the accompanying to be a -injective morphism becomes smaller and smaller, for it now lifts against all diagrams where factors through , which intuitively is less and less of a condition as the grow larger and larger.
The concept of small object is just what makes this intuition precise and finishes the small object argument. For the present purpose we just need the following simple version:
Definition
For a category and a sub-set of its morphisms, say that these have small domains if there is an ordinal (def. ) such that for every and for every -relative cell complex given by a transfinite composition (def. )
every morphism factors through a stage of order :
The above discussion proves the following:
Proposition
(small object argument)
Let be a locally small category with all small colimits. If a set of morphisms has all small domains in the sense of def. , then every morphism in factors through a -relative cell complex, def. , followed by a -injective morphism, def.
Homotopy
We discuss how the concept of homotopy is abstractly realized in model categories, def. .
Definition
Let be a model category, def. , and an object.
- A path space object for is a factorization of the diagonal as
where is a weak equivalence and is a fibration.
- A cylinder object for is a factorization of the codiagonal (or “fold map”) as
where is a weak equivalence. and is a cofibration.
Remark
For every object in a model category, a cylinder object and a path space object according to def. exist: the factorization axioms guarantee that there exists
-
a factorization of the codiagonal as
-
a factorization of the diagonal as
The cylinder and path space objects obtained this way are actually better than required by def. : in addition to being just a weak equivalence, for these this is actually an acyclic fibration, and dually in addition to being a weak equivalence, for these it is actually an acyclic cofibrations.
Some authors call cylinder/path-space objects with this extra property “very good” cylinder/path-space objects, respectively.
One may also consider dropping a condition in def. : what mainly matters is the weak equivalence, hence some authors take cylinder/path-space objects to be defined as in def. but without the condition that is a cofibration and without the condition that is a fibration. Such authors would then refer to the concept in def. as “good” cylinder/path-space objects.
The terminology in def. follows the original (Quillen 67, I.1 def. 4). With the induced concept of left/right homotopy below in def. , this admits a quick derivation of the key facts in the following, as we spell out below.
Lemma
Let be a model category. If is cofibrant, then for every cylinder object of , def. , not only is a cofibration, but each
is an acyclic cofibration separately.
Dually, if is fibrant, then for every path space object of , def. , not only is a cofibration, but each
is an acyclic fibration separately.
Proof
We discuss the case of the path space object. The other case is formally dual.
First, that the component maps are weak equivalences follows generally: by definition they have a right inverse and so this follows by two-out-of-three (def. ).
But if is fibrant, then also the two projection maps out of the product are fibrations, because they are both pullbacks of the fibration
hence is the composite of two fibrations, and hence itself a fibration, by prop. .
Path space objects are very non-unique as objects up to isomorphism:
Example
If is a fibrant object in a model category, def. , and for and two path space objects for , def. , then the fiber product is another path space object for : the pullback square
gives that the induced projection is again a fibration. Moreover, using lemma and two-out-of-three (def. ) gives that is a weak equivalence.
For the case of the canonical topological path space objects of def , with then this new path space object is , the mapping space out of the standard interval of length 2 instead of length 1.
Definition
(abstract left homotopy and abstract right homotopy
Let be two parallel morphisms in a model category.
- A left homotopy is a morphism from a cylinder object of , def. , such that it makes this diagram commute:
- A right homotopy is a morphism to some path space object of , def. , such that this diagram commutes:
Lemma
Let be two parallel morphisms in a model category.
-
Let be cofibrant. If there is a left homotopy then there is also a right homotopy (def. ) with respect to any chosen path space object.
-
Let be fibrant. If there is a right homotopy then there is also a left homotopy with respect to any chosen cylinder object.
In particular if is cofibrant and is fibrant, then by going back and forth it follows that every left homotopy is exhibited by every cylinder object, and every right homotopy is exhibited by every path space object.
Proof
We discuss the first case, the second is formally dual. Let be the given left homotopy. Lemma implies that we have a lift in the following commuting diagram
where on the right we have the chosen path space object. Now the composite is a right homotopy as required:
Proposition
For a cofibrant object in a model category and a fibrant object, then the relations of left homotopy and of right homotopy (def. ) on the hom set coincide and are both equivalence relations.
Proof
That both relations coincide under the (co-)fibrancy assumption follows directly from lemma .
The symmetry and reflexivity of the relation is obvious.
That right homotopy (hence also left homotopy) with domain is a transitive relation follows from using example to compose path space objects.
The homotopy category
We discuss the construction that takes a model category, def. , and then universally forces all its weak equivalences into actual isomorphisms.
Definition
(homotopy category of a model category)
Let be a model category, def. . Write for the category whose
-
objects are those objects of which are both fibrant and cofibrant;
-
morphisms are the homotopy classes of morphisms of , hence the equivalence classes of morphism under the equivalence relation of prop. ;
and whose composition operation is given on representatives by composition in .
This is, up to equivalence of categories, the homotopy category of the model category .
Proposition
Def. is well defined, in that composition of morphisms between fibrant-cofibrant objects in indeed passes to homotopy classes.
Proof
Fix any morphism between fibrant-cofibrant objects. Then for precomposition
to be well defined, we need that with also . But by prop we may take the homotopy to be exhibited by a right homotopy , for which case the statement is evident from this diagram:
For postcomposition we may choose to exhibit homotopy by left homotopy and argue dually.
We now spell out that def. indeed satisfies the universal property that defines the localization of a category with weak equivalences at its weak equivalences.
Lemma
(Whitehead theorem in model categories)
Let be a model category. A weak equivalence between two objects which are both fibrant and cofibrant is a homotopy equivalence (92).
Proof
By the factorization axioms in the model category and by two-out-of-three (def. ), every weak equivalence factors through an object as an acyclic cofibration followed by an acyclic fibration. In particular it follows that with and both fibrant and cofibrant, so is , and hence it is sufficient to prove that acyclic (co-)fibrations between such objects are homotopy equivalences.
So let be an acyclic fibration between fibrant-cofibrant objects, the case of acyclic cofibrations is formally dual. Then in fact it has a genuine right inverse given by a lift in the diagram
To see that is also a left inverse up to left homotopy, let be any cylinder object on (def. ), hence a factorization of the codiagonal on as a cofibration followed by a an acyclic fibration
and consider the commuting square
which commutes due to being a genuine right inverse of . By construction, this commuting square now admits a lift , and that constitutes a left homotopy .
Definition
(fibrant resolution and cofibrant resolution)
Given a model category , consider a choice for each object of
-
a factorization
of the initial morphism (Def. ), such that when is already cofibrant then ;
-
a factorization
of the terminal morphism (Def. ), such that when is already fibrant then .
Write then
for the functor to the homotopy category, def. , which sends an object to the object and sends a morphism to the homotopy class of the result of first lifting in
and then lifting (here: extending) in
Proof
First of all, the object is indeed both fibrant and cofibrant (as well as related by a zig-zag of weak equivalences to ):
Now to see that the image on morphisms is well defined. First observe that any two choices of the first lift in the definition are left homotopic to each other, exhibited by lifting in
Hence also the composites are left homotopic to each other, and since their domain is cofibrant, then by lemma they are also right homotopic by a right homotopy . This implies finally, by lifting in
that also and are right homotopic, hence that indeed represents a well-defined homotopy class.
Finally to see that the assignment is indeed functorial, observe that the commutativity of the lifting diagrams for and imply that also the following diagram commutes
Now from the pasting composite
one sees that is a lift of and hence the same argument as above gives that it is homotopic to the chosen .
For the following, recall the concept of natural isomorphism between functors: for two functors, then a natural transformation is for each object a morphism in , such that for each morphism in the following is a commuting square:
Such is called a natural isomorphism if its are isomorphisms for all objects .
Definition
(localization of a category category with weak equivalences)
For a category with weak equivalences, its localization at the weak equivalences is, if it exists,
such that
-
sends weak equivalences to isomorphisms;
-
is universal with this property, in that:
for any functor out of into any category , such that takes weak equivalences to isomorphisms, it factors through up to a natural isomorphism
and this factorization is unique up to unique isomorphism, in that for and two such factorizations, then there is a unique natural isomorphism making the evident diagram of natural isomorphisms commute.
Theorem
(convenient localization of model categories)
For a model category, the functor in def. (for any choice of and ) exhibits as indeed being the localization of the underlying category with weak equivalences at its weak equivalences, in the sense of def. :
Proof
First, to see that that indeed takes weak equivalences to isomorphisms: By two-out-of-three (def. ) applied to the commuting diagrams shown in the proof of lemma , the morphism is a weak equivalence if is:
With this the “Whitehead theorem for model categories”, lemma , implies that represents an isomorphism in .
Now let be any functor that sends weak equivalences to isomorphisms. We need to show that it factors as
uniquely up to unique natural isomorphism. Now by construction of and in def. , is the identity on the full subcategory of fibrant-cofibrant objects. It follows that if exists at all, it must satisfy for all with and both fibrant and cofibrant that
(hence in particular ).
But by def. that already fixes on all of , up to unique natural isomorphism. Hence it only remains to check that with this definition of there exists any natural isomorphism filling the diagram above.
To that end, apply to the above commuting diagram to obtain
Here now all horizontal morphisms are isomorphisms, by assumption on . It follows that defining makes the required natural isomorphism:
Remark
Due to theorem we may suppress the choices of cofibrant and fibrant replacement in def. and just speak of the localization functor
up to natural isomorphism.
In general, the localization of a category with weak equivalences (def. ) may invert more morphisms than just those in . However, if the category admits the structure of a model category , then its localization precisely only inverts the weak equivalences:
Proposition
(localization of model categories inverts precisely the weak equivalences)
Let be a model category (def. ) and let be its localization functor (def. , theorem ). Then a morphism in is a weak equivalence precisely if is an isomorphism in .
(e.g. Goerss-Jardine 96, II, prop 1.14)
While the construction of the homotopy category in def. combines the restriction to good (fibrant/cofibrant) objects with the passage to homotopy classes of morphisms, it is often useful to consider intermediate stages:
Definition
Given a model category , write
for the system of full subcategory inclusions of:
-
the category of fibrant-cofibrant objects ,
all regarded a categories with weak equivalences (def. ), via the weak equivalences inherited from , which we write , and .
Remark
(categories of fibrant objects and cofibration categories)
Of course the subcategories in def. inherit more structure than just that of categories with weak equivalences from . and each inherit “half” of the factorization axioms. One says that has the structure of a “fibration category” called a “Brown-category of fibrant objects”, while has the structure of a “cofibration category”.
We discuss properties of these categories of (co-)fibrant objects below in Homotopy fiber sequences.
The proof of theorem immediately implies the following:
Corollary
For a model category, the restriction of the localization functor from def. (using remark ) to any of the sub-categories with weak equivalences of def.
exhibits equivalently as the localization also of these subcategories with weak equivalences, at their weak equivalences. In particular there are equivalences of categories
The following says that for computing the hom-sets in the homotopy category, even a mixed variant of the above will do; it is sufficient that the domain is cofibrant and the codomain is fibrant:
Lemma
(hom-sets of homotopy category via mapping cofibrant resolutions into fibrant resolutions)
For with cofibrant and fibrant, and for fibrant/cofibrant replacement functors as in def. , then the morphism
(on homotopy classes of morphisms, well defined by prop. ) is a natural bijection.
Proof
We may factor the morphism in question as the composite
This shows that it is sufficient to see that for cofibrant and fibrant, then
is an isomorphism, and dually that
is an isomorphism. We discuss this for the former; the second is formally dual:
First, that is surjective is the lifting property in
which says that any morphism comes from a morphism under postcomposition with .
Second, that is injective is the lifting property in
which says that if two morphisms become homotopic after postcomposition with , then they were already homotopic before.
We record the following fact which will be used in part 1.1 (here):
Lemma
Let be a model category (def. ). Then every commuting square in its homotopy category (def. ) is, up to isomorphism of squares, in the image of the localization functor of a commuting square in (i.e.: not just commuting up to homotopy).
Proof
Let
be a commuting square in the homotopy category. Writing the same symbols for fibrant-cofibrant objects in and for morphisms in representing these, then this means that in there is a left homotopy of the form
Consider the factorization of the top square here through the mapping cylinder of
This exhibits the composite as an alternative representative of in , and as an alternative representative for , and the commuting square
as an alternative representative of the given commuting square in .
Derived functors
Definition
For and two categories with weak equivalences, def. , then a functor is called a homotopical functor if it sends weak equivalences to weak equivalences.
Definition
Given a homotopical functor (def. ) between categories with weak equivalences whose homotopy categories and exist (def. ), then its (“total”) derived functor is the functor between these homotopy categories which is induced uniquely, up to unique isomorphism, by their universal property (def. ):
Remark
While many functors of interest between model categories are not homotopical in the sense of def. , many become homotopical after restriction to the full subcategories of fibrant objects or of cofibrant objects, def. . By corollary this is just as good for the purpose of homotopy theory.
Therefore one considers the following generalization of def. :
Definition
(left and right derived functors)
Consider a functor out of a model category (def. ) into a category with weak equivalences (def. ).
-
If the restriction of to the full subcategory of fibrant object becomes a homotopical functor (def. ), then the derived functor of that restriction, according to def. , is called the right derived functor of and denoted by :
-
If the restriction of to the full subcategory of cofibrant object becomes a homotopical functor (def. ), then the derived functor of that restriction, according to def. , is called the left derived functor of and denoted by :
The key fact that makes def. practically relevant is the following:
Proposition
Let be a model category with full subcategories of fibrant objects and of cofibrant objects respectively (def. ). Let be a category with weak equivalences.
-
A functor out of the category of fibrant objects
is a homotopical functor, def. , already if it sends acyclic fibrations to weak equivalences.
-
A functor out of the category of cofibrant objects
is a homotopical functor, def. , already if it sends acyclic cofibrations to weak equivalences.
The following proof refers to the factorization lemma, whose full statement and proof we postpone to further below (lemma ).
Proof
We discuss the case of a functor on a category of fibrant objects , def. . The other case is formally dual.
Let be a weak equivalence in . Choose a path space object (def. ) and consider the diagram
where the square is a pullback and on the top left is our notation for the universal cone object. (Below we discuss this in more detail, it is the mapping cocone of , def. ).
Here:
-
is an acyclic fibration because it is the pullback of .
-
is a weak equivalence, because the factorization lemma states that the composite vertical morphism factors through a weak equivalence, hence if is a weak equivalence, then is by two-out-of-three (def. ).
Now apply the functor to this diagram and use the assumption that it sends acyclic fibrations to weak equivalences to obtain
But the factorization lemma , in addition says that the vertical composite is a fibration, hence an acyclic fibration by the above. Therefore also is a weak equivalence. Now the claim that also is a weak equivalence follows with applying two-out-of-three (def. ) twice.
Corollary
Let be model categories and consider a functor. Then:
-
If preserves cofibrant objects and acyclic cofibrations between these, then its left derived functor (def. ) exists, fitting into a diagram
-
If preserves fibrant objects and acyclic fibrants between these, then its right derived functor (def. ) exists, fitting into a diagram
Proposition
(construction of left/right derived functors)
Let be a functor between two model categories (def. ).
-
If preserves fibrant objects and weak equivalences between fibrant objects, then the total right derived functor (def. ) in
is given, up to isomorphism, on any object by appying to a fibrant replacement of and then forming a cofibrant replacement of the result:
-
If preserves cofibrant objects and weak equivalences between cofibrant objects, then the total left derived functor (def. ) in
is given, up to isomorphism, on any object by appying to a cofibrant replacement of and then forming a fibrant replacement of the result:
Proof
We discuss the first case, the second is formally dual. By the proof of theorem we have
But since is a homotopical functor on fibrant objects, the cofibrant replacement morphism is a weak equivalence in , hence becomes an isomorphism under . Therefore
Now since is assumed to preserve fibrant objects, is fibrant in , and hence acts on it (only) by cofibrant replacement.
Quillen adjunctions
In practice it turns out to be useful to arrange for the assumptions in corollary to be satisfied by pairs of adjoint functors (Def. ). Recall that this is a pair of functors and going back and forth between two categories
such that there is a natural bijection between hom-sets with on the left and those with on the right (10):
for all objects and . This being natural (Def. ) means that is a natural transformation, hence that for all morphisms and the following is a commuting square:
We write to indicate such an adjunction and call the left adjoint and the right adjoint of the adjoint pair.
The archetypical example of a pair of adjoint functors is that consisting of forming Cartesian products and forming mapping spaces , as in the category of compactly generated topological spaces of def. .
If is any morphism, then the image is called its adjunct, and conversely. The fact that adjuncts are in bijection is also expressed by the notation
For an object , the adjunct of the identity on is called the adjunction unit .
For an object , the adjunct of the identity on is called the adjunction counit .
Adjunction units and counits turn out to encode the adjuncts of all other morphisms by the formulas
-
.
Definition
Let be model categories. A pair of adjoint functors (Def. ) between them
is called a Quillen adjunction, to be denoted
and , are called left/right Quillen functors, respectively, if the following equivalent conditions are satisfied:
-
preserves cofibrations and preserves fibrations;
-
preserves acyclic cofibrations and preserves acyclic fibrations;
-
preserves cofibrations and acyclic cofibrations;
-
preserves fibrations and acyclic fibrations.
Proof
First observe that
-
(i) A left adjoint between model categories preserves acyclic cofibrations precisely if its right adjoint preserves fibrations.
-
(ii) A left adjoint between model categories preserves cofibrations precisely if its right adjoint preserves acyclic fibrations.
We discuss statement (i), statement (ii) is formally dual. So let be an acyclic cofibration in and a fibration in . Then for every commuting diagram as on the left of the following, its -adjunct is a commuting diagram as on the right here:
If preserves acyclic cofibrations, then the diagram on the right has a lift, and so the -adjunct of that lift is a lift of the left diagram. This shows that has the right lifting property against all acylic cofibrations and hence is a fibration. Conversely, if preserves fibrations, the same argument run from right to left gives that preserves acyclic fibrations.
Now by repeatedly applying (i) and (ii), all four conditions in question are seen to be equivalent.
The following is the analog of adjunction unit and adjunction counit (Def. ):
Definition
Let and be model categories (Def. ), and let
be a Quillen adjunction (Def. ). Then
-
a derived adjunction unit at an object is a composition of the form
where
-
is the ordinary adjunction unit (Def. );
-
is a cofibrant resolution in (Def. );
-
is a fibrant resolution in (Def. );
-
-
a derived adjunction counit at an object is a composition of the form
where
-
is the ordinary adjunction counit (Def. );
-
is a fibrant resolution in (Def. );
-
is a cofibrant resolution in (Def. ).
-
We will see that Quillen adjunctions induce ordinary adjoint pairs of derived functors on homotopy categories (Prop. ). For this we first consider the following technical observation:
Lemma
(right Quillen functors preserve path space objects)
Let be a Quillen adjunction, def. .
-
For a fibrant object and a path space object (def. ), then is a path space object for .
-
For a cofibrant object and a cylinder object (def. ), then is a cylinder object for .
Proof
Consider the second case, the first is formally dual.
First Observe that because is left adjoint and hence preserves colimits, hence in particular coproducts.
Hence
is a cofibration.
Second, with cofibrant then also is a cofibrantion, since is a cofibration (lemma ). Therefore by Ken Brown's lemma (prop. ) preserves the weak equivalence .
Proposition
For a Quillen adjunction, def. , also the corresponding left and right derived functors (Def. , via cor. ) form a pair of adjoint functors
Moreover, the adjunction unit and adjunction counit of this derived adjunction are the images of the derived adjunction unit and derived adjunction counit (Def. ) under the localization functors (Theorem ).
Proof
For the first statement, by def. and lemma it is sufficient to see that for with cofibrant and fibrant, then there is a natural bijection
Since by the adjunction isomorphism for such a natural bijection exists before passing to homotopy classes , it is sufficient to see that this respects homotopy classes. To that end, use from lemma that with a cylinder object for , def. , then is a cylinder object for . This implies that left homotopies
given by
are in bijection to left homotopies
given by
This establishes the adjunction. Now regarding the (co-)units: We show this for the adjunction unit, the case of the adjunction counit is formally dual.
First observe that for , then the defining commuting square for the left derived functor from def.
(using fibrant and fibrant/cofibrant replacement functors , from def. with their universal property from theorem , corollary ) gives that
where the second isomorphism holds because the left Quillen functor sends the acyclic cofibration to a weak equivalence.
The adjunction unit of on is the image of the identity under
By the above and the proof of prop. , that adjunction isomorphism is equivalently that of under the isomorphism
of lemma . Hence the derived adjunction unit (Def. ) is the -adjunct of
which indeed (by the formula for adjuncts, Prop. ) is the derived adjunction unit
This suggests to regard passage to homotopy categories and derived functors as itself being a suitable functor from a category of model categories to the category of categories. Due to the role played by the distinction between left Quillen functors and right Quillen functors, this is usefully formulated as a double functor:
Definition
(double category of model categories)
The (very large) double category of model categories is the double category (Def. ) that has
-
as objects: model categories (Def. );
-
as vertical morphisms: left Quillen functors (Def. );
-
as horizontal morphisms: right Quillen functors (Def. );
-
as 2-morphisms natural transformations between the composites of underlying functors:
and composition is given by ordinary composition of functors, horizontally and vertically, and by whiskering-composition of natural transformations.
There is hence a forgetful double functor (Remark )
to the double category of squares (Example ) in the 2-category of categories (Example ), which forgets the model category-structure and the Quillen functor-property.
The following records the 2-functoriality of sending Quillen adjunctions to adjoint pairs of derived functors (Prop. ):
Proposition
(homotopy double pseudofunctor on the double category of model categories)
There is a double pseudofunctor (Remark )
from the double category of model categories (Def. ) to the double category of squares (Example ) in the 2-category Cat (Example ), which sends
-
a model category to its homotopy category of a model category (Def. );
-
a left Quillen functor (Def. ) to its left derived functor (Def. );
-
a right Quillen functor (Def. ) to its right derived functor (Def. );
-
to the “derived natural transformation”
given by the zig-zag
(94)where the unlabeled morphisms are induced by fibrant resolution and cofibrant resolution , respectively (Def. ).
Lemma
(recognizing derived natural isomorphisms)
For the derived natural transformation in (94) to be invertible in the homotopy category, it is sufficient that for every object which is both fibrant and cofibrant the following composite natural transformation
(of with images of fibrant resolution/cofibrant resolution, Def. ) is invertible in the homotopy category, hence that the composite is a weak equivalence (by Prop. ).
Example
(derived functor of left-right Quillen functor)
Let , be model categories (Def. ), and let
be a functor that is both a left Quillen functor as well as a right Quillen functor (Def. ). This means equivalently that there is a 2-morphism in the double category of model categories (Def. ) of the form
It follows that the left derived functor and right derived functor of (Def. ) are naturally isomorphic:
Proof
To see the natural isomorphism : By Prop. this is implied once the derived natural transformation of (95) is a natural isomorphism. By Prop. this is the case, in the present situation, if the composition of
is a weak equivalence. But this is immediate, since the two factors are weak equivalences, by definition of fibrant/cofibrant resolution (Def. ).
The following is the analog of co-reflective subcategories (Def. ) for model categories:
Definition
Let and be model categories (Def. ), and let
be a Quillen adjunction between them (Def. ). Then this may be called
-
a Quillen reflection if the derived adjunction counit (Def. ) is componentwise a weak equivalence;
-
a Quillen co-reflection if the derived adjunction unit (Def. ) is componentwise a weak equivalence.
The main class of examples of Quillen reflections are left Bousfield localizations, discussed as Prop. below.
Proposition
(characterization of Quillen reflections)
Let
be a Quillen adjunction (Def. ) and write
for the induced adjoint pair of derived functors on the homotopy categories, from Prop. .
Then
-
is a Quillen reflection (Def. ) precisely if is a reflective subcategory-inclusion (Def. );
-
is a Quillen co-reflection] (Def. ) precisely if is a co-reflective subcategory-inclusion (Def. );
Proof
By Prop. the components of the adjunction unit/counit of are precisely the images under localization of the derived adjunction unit/counit of . Moreover, by Prop. the localization functor of a model category inverts precisely the weak equivalences. Hence the adjunction (co-)unit of is an isomorphism if and only if the derived (co-)unit of is a weak equivalence, respectively.
With this the statement reduces to the characterization of (co-)reflections via invertible units/counits, respectively, from Prop. .
The following is the analog of adjoint equivalence of categories (Def. ) for model categories:
Definition
For two model categories (Def. ), a Quillen adjunction (def. )
is called a Quillen equivalence, to be denoted
if the following equivalent conditions hold:
-
The right derived functor of (via prop. , corollary ) is an equivalence of categories
-
The left derived functor of (via prop. , corollary ) is an equivalence of categories
-
For every cofibrant object , the derived adjunction unit (Def. )
is a weak equivalence;
and for every fibrant object , the derived adjunction counit (Def. )
is a weak equivalence.
-
For every cofibrant object and every fibrant object , a morphism is a weak equivalence precisely if its adjunct morphism is:
Proof
That follows from prop. (if in an adjoint pair one is an equivalence, then so is the other).
To see the equivalence , notice (prop.) that a pair of adjoint functors is an equivalence of categories precisely if both the adjunction unit and the adjunction counit are natural isomorphisms. Hence it is sufficient to see that the derived adjunction unit/derived adjunction counit (Def. ) indeed represent the adjunction (co-)unit of in the homotopy category. But this is the statement of Prop. .
To see that :
Consider the weak equivalence . Its -adjunct is
by assumption 4) this is again a weak equivalence, which is the requirement for the derived adjunction unit in 3). Dually for derived adjunction counit.
To see :
Consider any a weak equivalence for cofibrant , firbant . Its adjunct sits in a commuting diagram
where is any lift constructed as in def. .
This exhibits the bottom left morphism as the derived adjunction unit (Def. ), hence a weak equivalence by assumption. But since was a weak equivalence, so is (by two-out-of-three). Thereby also and , are weak equivalences by Ken Brown's lemma and the assumed fibrancy of . Therefore by two-out-of-three (def. ) also the adjunct is a weak equivalence.
Example
(trivial Quillen equivalence)
Let be a model category (Def. ). Then the identity functor on constitutes a Quillen equivalence (Def. ) from to itself:
Proof
From prop. it is clear that in this case the derived functors and both are themselves the identity functor on the homotopy category of a model category, hence in particular are an equivalence of categories.
In certain situations the conditions on a Quillen equivalence simplify. For instance:
Proposition
(recognition of Quillen equivalences)
If in a Quillen adjunction (def. ) the right adjoint “creates weak equivalences” (in that a morphism in is a weak equivalence precisly if is) then is a Quillen equivalence (def. ) precisely already if for all cofibrant objects the plain adjunction unit
is a weak equivalence.
Proof
By prop. , generally, is a Quillen equivalence precisely if
-
for every cofibrant object , the derived adjunction unit (Def. )
is a weak equivalence;
-
for every fibrant object , the derived adjunction counit (Def. )
is a weak equivalence.
Consider the first condition: Since preserves the weak equivalence , then by two-out-of-three (def. ) the composite in the first item is a weak equivalence precisely if is.
Hence it is now sufficient to show that in this case the second condition above is automatic.
Since also reflects weak equivalences, the composite in item two is a weak equivalence precisely if its image
under is.
Moreover, assuming, by the above, that on the cofibrant object is a weak equivalence, then by two-out-of-three this composite is a weak equivalence precisely if the further composite with is
By the formula for adjuncts, this composite is the -adjunct of the original composite, which is just
But is a weak equivalence by definition of cofibrant replacement.
The following is the analog of adjoint triples, adjoint quadruples (Remark ), etc. for model categories:
Definition
Let be model categories (Def. ), where and share the same underlying category , and such that the identity functor on constitutes a Quillen equivalence (Def. ):
Then
-
a Quillen adjoint triple of the form
is diagrams in the double category of model categories (Def. ) of the form
such that is the unit of an adjunction and the counit of an adjunction, thus exhibiting Quillen adjunctions
and such that the derived natural transformation of the bottom right square (94) is invertible (a natural isomorphism);
-
a Quillen adjoint triple of the form
is diagram in the double category of model categories (Def. ) of the form
such that is the unit of an adjunction and the counit of an adjunction, thus exhibiting Quillen adjunctions
and such that the derived natural transformation of the top left square square (here) is invertible (a natural isomorphism).
If a Quillen adjoint triple of the first kind overlaps with one of the second kind
we speak of a Quillen adjoint quadruple, and so forth.
Proposition
(Quillen adjoint triple induces adjoint triple of derived functors on homotopy categories)
Given a Quillen adjoint triple (Def. ), the induced derived functors (Def. ) on the homotopy categories form an ordinary adjoint triple (Remark ):
Proof
This follows immediately from the fact that passing to homotopy categories of model categories is a double pseudofunctor from the double category of model categories to the double category of squares in Cat (Prop. ).
Mapping cones
In the context of homotopy theory, a pullback diagram, such as in the definition of the fiber in example
ought to commute only up to a (left/right) homotopy (def. ) between the outer composite morphisms. Moreover, it should satisfy its universal property up to such homotopies.
Instead of going through the full theory of what this means, we observe that this is plausibly modeled by the following construction, and then we check (below) that this indeed has the relevant abstract homotopy theoretic properties.
Definition
Let be a model category, def. with its model structure on pointed objects, prop. . For a morphism between cofibrant objects (hence a morphism in , def. ), its reduced mapping cone is the object
in the colimiting diagram
where is a cylinder object for , def. .
Dually, for a morphism between fibrant objects (hence a morphism in , def. ), its mapping cocone is the object
in the following limit diagram
where is a path space object for , def. .
Remark
When we write homotopies (def. ) as double arrows between morphisms, then the limit diagram in def. looks just like the square in the definition of fibers in example , except that it is filled by the right homotopy given by the component map denoted :
Dually, the colimiting diagram for the mapping cone turns to look just like the square for the cofiber, except that it is filled with a left homotopy
Proposition
The colimit appearing in the definition of the reduced mapping cone in def. is equivalent to three consecutive pushouts:
The two intermediate objects appearing here are called
-
the plain reduced cone ;
-
the reduced mapping cylinder .
Dually, the limit appearing in the definition of the mapping cocone in def. is equivalent to three consecutive pullbacks:
The two intermediate objects appearing here are called
-
the based path space object ;
-
the mapping path space or mapping co-cylinder .
Definition
Let be any pointed object.
-
The mapping cone, def. , of is called the reduced suspension of , denoted
Via prop. this is equivalently the coproduct of two copies of the cone on over their base:
This is also equivalently the cofiber, example of , hence (example ) of the wedge sum inclusion:
-
The mapping cocone, def. , of is called the loop space object of , denoted
Via prop. this is equivalently
This is also equivalently the fiber, example of :
Proposition
In pointed topological spaces ,
-
the reduced suspension objects (def. ) induced from the standard reduced cylinder of example are isomorphic to the smash product (def. ) with the 1-sphere, for later purposes we choose to smash on the left and write
Dually:
-
the loop space objects (def. ) induced from the standard pointed path space object are isomorphic to the pointed mapping space (example ) with the 1-sphere
Proof
By immediate inspection: For instance the fiber of is clearly the subspace of the unpointed mapping space on elements that take the endpoints of to the basepoint of .
Example
For Top with the standard cyclinder object, def. , then by example , the mapping cone, def. , of a continuous function is obtained by
-
forming the cylinder over ;
-
attaching to one end of that cylinder the space as specified by the map .
-
shrinking the other end of the cylinder to the point.
Accordingly the suspension of a topological space is the result of shrinking both ends of the cylinder on the object two the point. This is homeomoprhic to attaching two copies of the cone on the space at the base of the cone.
(graphics taken from Muro 2010)
Below in example we find the homotopy-theoretic interpretation of this standard topological mapping cone as a model for the homotopy cofiber.
Remark
The formula for the mapping cone in prop. (as opposed to that of the mapping co-cone) does not require the presence of the basepoint: for a morphism in (as opposed to in ) we may still define
where the prime denotes the unreduced cone, formed from a cylinder object in .
Proposition
For a morphism in Top, then its unreduced mapping cone, remark , with respect to the standard cylinder object def. , is isomorphic to the reduced mapping cone, def. , of the morphism (with a basepoint adjoined, def. ) with respect to the standard reduced cylinder (example ):
Proof
By prop. and example , is given by the colimit in over the following diagram:
We may factor the vertical maps to give
This way the top part of the diagram (using the pasting law to compute the colimit in two stages) is manifestly a cocone under the result of applying to the diagram for the unreduced cone. Since is itself given by a colimit, it preserves colimits, and hence gives the partial colimit as shown. The remaining pushout then contracts the remaining copy of the point away.
Example makes it clear that every cycle in that happens to be in the image of can be continuously translated in the cylinder-direction, keeping it constant in , to the other end of the cylinder, where it shrinks away to the point. This means that every homotopy group of , def. , in the image of vanishes in the mapping cone. Hence in the mapping cone the image of under in is removed up to homotopy. This makes it intuitively clear how is a homotopy-version of the cokernel of . We now discuss this formally.
Lemma
Let be a category of cofibrant objects, def. . Then for every morphism the mapping cylinder-construction in def. provides a cofibration resolution of , in that
-
the composite morphism is a cofibration;
-
factors through this morphism by a weak equivalence left inverse to an acyclic cofibration
Dually:
Let be a category of fibrant objects, def. . Then for every morphism the mapping cocylinder-construction in def. provides a fibration resolution of , in that
-
the composite morphism is a fibration;
-
factors through this morphism by a weak equivalence right inverse to an acyclic fibration:
Proof
We discuss the second case. The first case is formally dual.
So consider the mapping cocylinder-construction from prop.
To see that the vertical composite is indeed a fibration, notice that, by the pasting law, the above pullback diagram may be decomposed as a pasting of two pullback diagram as follows
Both squares are pullback squares. Since pullbacks of fibrations are fibrations by prop. , the morphism is a fibration. Similarly, since is fibrant, also the projection map is a fibration (being the pullback of along ).
Since the vertical composite is thereby exhibited as the composite of two fibrations
it is itself a fibration.
Then to see that there is a weak equivalence as claimed:
The universal property of the pullback induces a right inverse of fitting into this diagram
which is a weak equivalence, as indicated, by two-out-of-three (def. ).
This establishes the claim.
Categories of fibrant objects
Below we discuss the homotopy-theoretic properties of the mapping cone- and mapping cocone-constructions from above. Before we do so, we here establish a collection of general facts that hold in categories of fibrant objects and dually in categories of cofibrant objects, def. .
Literature (Brown 73, section 4).
Lemma
Let be a morphism in a category of fibrant objects, def. . Then given any choice of path space objects and , def. , there is a replacement of by a path space object along an acylic fibration, such that has a morphism to which is compatible with the structure maps, in that the following diagram commutes
(Brown 73, section 2, lemma 2)
Proof
Consider the commuting square
Then consider its factorization through the pullback of the right morphism along the bottom morphism,
Finally use the factorization lemma to factor the morphism through a weak equivalence followed by a fibration, the object this factors through serves as the desired path space resolution
Lemma
In a category of fibrant objects , def. , let
be a morphism over some object in and let be any morphism in . Let
be the corresponding morphism pulled back along .
Then
-
if is a fibration then also is a fibration;
-
if is a weak equivalence then also is a weak equivalence.
(Brown 73, section 4, lemma 1)
Proof
For the statement follows from the pasting law which says that if in
the bottom and the total square are pullback squares, then so is the top square. The same reasoning applies for .
Now to see the case that :
Consider the full subcategory of the slice category (def. ) on its fibrant objects, i.e. the full subcategory of the slice category on the fibrations
into . By factorizing for every such fibration the diagonal morphisms into the fiber product through a weak equivalence followed by a fibration, we obtain path space objects relative to :
With these, the factorization lemma (lemma ) applies in .
(Notice that for this we do need the restriction of to the fibrations, because this ensures that the projections are still fibrations, which is used in the proof of the factorization lemma (here).)
So now given any
apply the factorization lemma in to factor it as
By the previous discussion it is sufficient now to show that the base change of to is still a weak equivalence. But by the factorization lemma in , the morphism is right inverse to another acyclic fibration over :
(Notice that if we had applied the factorization lemma of in instead of in then the corresponding triangle on the right here would not commute.)
Now we may reason as before: the base change of the top morphism here is exhibited by the following pasting composite of pullbacks:
The acyclic fibration is preserved by this pullback, as is the identity . Hence the weak equivalence is preserved by two-out-of-three (def. ).
Lemma
In a category of fibrant objects, def. , the pullback of a weak equivalence along a fibration is again a weak equivalence.
(Brown 73, section 4, lemma 2)
Proof
Let be a weak equivalence and be a fibration. We want to show that the left vertical morphism in the pullback
is a weak equivalence.
First of all, using the factorization lemma we may factor as
with the first morphism a weak equivalence that is a right inverse to an acyclic fibration and the right one an acyclic fibration.
Then the pullback diagram in question may be decomposed into two consecutive pullback diagrams
where the morphisms are indicated as fibrations and acyclic fibrations using the stability of these under arbitrary pullback.
This means that the proof reduces to proving that weak equivalences that are right inverse to some acyclic fibration map to a weak equivalence under pullback along a fibration.
Given such with right inverse , consider the pullback diagram
Notice that the indicated universal morphism into the pullback is a weak equivalence by two-out-of-three (def. ).
The previous lemma says that weak equivalences between fibrations over are themselves preserved by base extension along . In total this yields the following diagram
so that with a weak equivalence also is a weak equivalence, as indicated.
Notice that is the morphism that we want to show is a weak equivalence. By two-out-of-three (def. ) for that it is now sufficient to show that is a weak equivalence.
That finally follows now since, by assumption, the total bottom horizontal morphism is the identity. Hence so is the top horizontal morphism. Therefore is right inverse to a weak equivalence, hence is a weak equivalence.
Lemma
Let be a category of fibrant objects, def. in a model structure on pointed objects (prop. ). Given any commuting diagram in of the form
(meaning: both squares commute and equalizes with ) then the localization functor (def. , cor ) takes the morphisms induced by and on fibers (example ) to the same morphism, in the homotopy category.
(Brown 73, section 4, lemma 4)
Proof
First consider the pullback of along : this forms the same kind of diagram but with the bottom morphism an identity. Hence it is sufficient to consider this special case.
Consider the full subcategory of the slice category (def. ) on its fibrant objects, i.e. the full subcategory of the slice category on the fibrations
into . By factorizing for every such fibration the diagonal morphisms into the fiber product through a weak equivalence followed by a fibration, we obtain path space objects relative to :
With these, the factorization lemma (lemma ) applies in .
Let then be a path space object for in the slice over and consider the following commuting square
By factoring this through the pullback and then applying the factorization lemma and then two-out-of-three (def. ) to the factoring morphisms, this may be replaced by a commuting square of the same form, where however the left morphism is an acyclic fibration
This makes also the morphism be a fibration, so that the whole diagram may now be regarded as a diagram in the category of fibrant objects of the slice category over .
As such, the top horizontal morphism now exhibits a right homotopy which under localization (def. ) of the slice model structure (prop. ) we have
The result then follows by observing that we have a commuting square of functors
because, by lemma , the top and right composite sends weak equivalences to isomorphisms, and hence the bottom filler exists by theorem . This implies the claim.
Homotopy fibers
We now discuss the homotopy-theoretic properties of the mapping cone- and mapping cocone-constructions from above.
Literature (Brown 73, section 4).
Remark
The factorization lemma with prop. says that the mapping cocone of a morphism , def. , is equivalently the plain fiber, example , of a fibrant resolution of :
The following prop. says that, up to equivalence, this situation is independent of the specific fibration resolution provided by the factorization lemma (hence by the prescription for the mapping cocone), but only depends on it being some fibration resolution.
Proposition
In the category of fibrant objects , def. , of a model structure on pointed objects (prop. ) consider a morphism of fiber-diagrams, hence a commuting diagram of the form
If and weak equivalences, then so is .
Proof
Factor the diagram in question through the pullback of along
and observe that
-
;
-
is a weak equivalence by assumption and by two-out-of-three (def. );
Moreover, this diagram exhibits as the base change, along , of . Therefore the claim now follows with lemma .
Hence we say:
Definition
Let be a model category and its model category of pointed objects, prop. . For any morphism in its category of fibrant objects , def. , then its homotopy fiber
is the morphism in the homotopy category , def. , which is represented by the fiber, example , of any fibration resolution of (hence any fibration such that factors through a weak equivalence followed by ).
Dually:
For any morphism in its category of cofibrant objects , def. , then its homotopy cofiber
is the morphism in the homotopy category , def. , which is represented by the cofiber, example , of any cofibration resolution of (hence any cofibration such that factors as followed by a weak equivalence).
Proposition
The homotopy fiber in def. is indeed well defined, in that for and two fibration replacements of any morphisms in , then their fibers are isomorphic in .
Proof
It is sufficient to exhibit an isomorphism in from the fiber of the fibration replacement given by the factorization lemma (for any choice of path space object) to the fiber of any other fibration resolution.
Hence given a morphism and a factorization
consider, for any choice of path space object (def. ), the diagram
as in the proof of lemma . Now by repeatedly using prop. :
-
the bottom square gives a weak equivalence from the fiber of to the fiber of ;
-
The square
gives a weak equivalence from the fiber of to the fiber of .
-
Similarly the total vertical composite gives a weak equivalence via
from the fiber of to the fiber of .
Together this is a zig-zag of weak equivalences of the form
between the fiber of and the fiber of . This gives an isomorphism in the homotopy category.
Example
(fibers of Serre fibrations)
In showing that Serre fibrations are abstract fibrations in the sense of model category theory, theorem implies that the fiber (example ) of a Serre fibration, def.
over any point is actually a homotopy fiber in the sense of def. . With prop. this implies that the weak homotopy type of the fiber only depends on the Serre fibration up to weak homotopy equivalence in that if is another Serre fibration fitting into a commuting diagram of the form
then .
In particular this gives that the weak homotopy type of the fiber of a Serre fibration does not change as the basepoint is moved in the same connected component. For let be a path between two points
Then since all objects in are fibrant, and since the endpoint inclusions are weak equivalences, lemma gives the zig-zag of top horizontal weak equivalences in the following diagram:
and hence an isomorphism in the classical homotopy category (def. ).
The same kind of argument applied to maps from the square gives that if are two homotopic paths with coinciding endpoints, then the isomorphisms between fibers over endpoints which they induce are equal. (But in general the isomorphism between the fibers does depend on the choice of homotopy class of paths connecting the basepoints!)
The same kind of argument also shows that if has the structure of a cell complex (def. ) then the restriction of the Serre fibration to one cell may be identified in the homotopy category with , and may be canonically identified so if the fundamental group of is trivial. This is used when deriving the Serre-Atiyah-Hirzebruch spectral sequence for (prop.).
Example
For every continuous function between CW-complexes, def. , then the standard topological mapping cone is the attaching space (example )
of with the standard cone given by collapsing one end of the standard topological cyclinder (def. ) as shown in example .
Equipped with the canonical continuous function
this represents the homotopy cofiber, def. , of with respect to the classical model structure on topological spaces from theorem .
Proof
By prop. , for a CW-complex then the standard topological cylinder object is indeed a cyclinder object in . Therefore by prop. and the factorization lemma , the mapping cone construction indeed produces first a cofibrant replacement of and then the ordinary cofiber of that, hence a model for the homotopy cofiber.
Example
The homotopy fiber of the inclusion of classifying spaces is the n-sphere . See this prop. at Classifying spaces and G-structure.
Example
Suppose a morphism already happens to be a fibration between fibrant objects. The factorization lemma replaces it by a fibration out of the mapping cocylinder , but such that the comparison morphism is a weak equivalence:
Hence by prop. in this case the ordinary fiber of is weakly equivalent to the mapping cocone, def. .
We may now state the abstract version of the statement of prop. :
Proposition
Let be a model category. For any morphism of pointed objects, and for a pointed object, def. , then the sequence
is exact as a sequence of pointed sets.
(Where the sequence here is the image of the homotopy fiber sequence of def. under the hom-functor from example .)
Proof
Let , and denote fibrant-cofibrant objects in representing the given objects of the same name in . Moreover, let be a fibration in representing the given morphism of the same name in .
Then by def. and prop. there is a representative of the homotopy fiber which fits into a pullback diagram of the form
With this the hom-sets in question are represented by genuine morphisms in , modulo homotopy. From this it follows immediately that includes into . Hence it remains to show the converse: that every element in indeed comes from .
But an element in is represented by a morphism such that there is a left homotopy as in the following diagram
Now by lemma the square here has a lift , as shown. This means that is left homotopic to . But by the universal property of the fiber, factors through .
With prop. it also follows notably that the loop space construction becomes well-defined on the homotopy category:
Remark
Given an object , and picking any path space object , def. with induced loop space object , def. , write for the path space object given by the fiber product of with itself, via example . From the pullback diagram there, the fiber inclusion induces a morphism
In the case where and is induced, via def. , from the standard path space object (def. ), i.e. in the case that
then this is the operation of concatenating two loops parameterized by to a single loop parameterized by .
Proposition
Let be a model category, def. . Then the construction of forming loop space objects , def. (which on depends on a choice of path space objects, def. ) becomes unique up to isomorphism in the homotopy category (def. ) of the model structure on pointed objects (prop. ) and extends to a functor:
Dually, the reduced suspension operation, def. , which on depends on a choice of cylinder object, becomes a functor on the homotopy category
Moreover, the pairing operation induced on the objects in the image of this functor via remark (concatenation of loops) gives the objects in the image of group object structure, and makes this functor lift as
(Brown 73, section 4, theorem 3)
Proof
Given an object and given two choices of path space objects and , we need to produce an isomorphism in between and .
To that end, first lemma implies that any two choices of path space objects are connected via a third path space by a span of morphisms compatible with the structure maps. By two-out-of-three (def. ) every morphism of path space objects compatible with the inclusion of the base object is a weak equivalence. With this, lemma implies that these morphisms induce weak equivalences on the corresponding loop space objects. This shows that all choices of loop space objects become isomorphic in the homotopy category.
Moreover, all the isomorphisms produced this way are actually equal: this follows from lemma applied to
This way we obtain a functor
By prop. (and using that Cartesian product preserves weak equivalences) this functor sends weak equivalences to isomorphisms. Therefore the functor on homotopy categories now follows with theorem .
It is immediate to see that the operation of loop concatenation from remark gives the objects the structure of monoids. It is now sufficient to see that these are in fact groups:
We claim that the inverse-assigning operation is given by the left map in the following pasting composite
(where , thus defined, is the path space object obtained from by “reversing the notion of source and target of a path”).
To see that this is indeed an inverse, it is sufficient to see that the two morphisms
induced from
coincide in the homotopy category. This follows with lemma applied to the following commuting diagram:
Homotopy pullbacks
The concept of homotopy fibers of def. is a special case of the more general concept of homotopy pullbacks.
Definition
A model category (def. ) is called
-
a right proper model category if pullback along fibrations preserves weak equivalences;
-
a left proper model category if pushout along cofibrations preserves weak equivalences;
-
a proper model category if it is both left and right proper.
Example
By lemma , a model category (def. ) in which all objects are fibrant is a right proper model category (def. ).
Definition
Let be a right proper model category (def. ). Then a commuting square
in is called a homotopy pullback (of along and equivalently of along ) if the following equivalent conditions hold:
-
for some factorization of the form
the universally induced morphism from into the pullback of along is a weak equivalence:
-
for some factorization of the form
the universally induced morphism from into the pullback of along is a weak equivalence:
-
the above two conditions hold for every such factorization.
(e.g. Goerss-Jardine 96, II (8.14))
Proof
First assume that the first condition holds, in that
Then let
be any factorization of and consider the pasting diagram (using the pasting law for pullbacks)
where the inner morphisms are fibrations and weak equivalences, as shown, by the pullback stability of fibrations (prop. ) and then since pullback along fibrations preserves weak equivalences by assumption of right properness (def. ). Hence it follows by two-out-of-three (def. ) that also the comparison morphism is a weak equivalence.
In conclusion, if the homotopy pullback condition is satisfied for one factorization of , then it is satisfied for all factorizations of . Since the argument is symmetric in and , this proves the claim.
Remark
In particular, an ordinary pullback square of fibrant objects, one of whose edges is a fibration, is a homotopy pullback square according to def. .
Proposition
Let be a right proper model category (def. ). Given a diagram in of the form
then the induced morphism on pullbacks is a weak equivalence
Proof
(The reader should draw the 3-dimensional cube diagram which we describe in words now.)
First consider the universal morphism and observe that it is a weak equivalence by right properness (def. ) and two-out-of-three (def. ).
Then consider the universal morphism and observe that this is also a weak equivalence, since is the limiting cone of a homotopy pullback square by remark , and since the morphism is the comparison morphism to the pullback of the factorization constructed in the first step.
Now by using the pasting law, then the commutativity of the “left” face of the cube, then the pasting law again, one finds that . Again by right properness this implies that is a weak equivalence.
With this the claim follows by two-out-of-three.
Homotopy pullbacks satisfy the usual abstract properties of pullbacks:
Proposition
Let be a right proper model category (def. ). If in a commuting square in one edge is a weak equivalence, then the square is a homotopy pullback square precisely if the opposite edge is a weak equivalence, too.
Proof
Consider a commuting square of the form
To detect whether this is a homotopy pullback, by def. and prop. , we are to choose any factorization of the right vertical morphism to obtain the pasting composite
Here the morphism in the middle is a weak equivalence by right properness (def. ). Hence it follows by two-out-of-three that the top left comparison morphism is a weak equivalence (and so the original square is a homotopy pullback) precisely if the top morphism is a weak equivalence.
Proposition
Let be a right proper model category (def. ).
-
(pasting law) If in a commuting diagram
the square on the right is a homotoy pullback (def. ) then the left square is, too, precisely if the total rectangle is;
-
in the presence of functorial factorization (def. ) through weak equivalences followed by fibrations:
every retract of a homotopy pullback square (in the category of commuting squares in ) is itself a homotopy pullback square.
Proof
For the first statement: choose a factorization of , pull it back to a factorization and assume that is a weak equivalence, i.e. that the right square is a homotopy pullback. Now use the ordinary pasting law to conclude.
For the second statement: functorially choose a factorization of the two right vertical morphisms of the squares and factor the squares through the pullbacks of the corresponding fibrations along the bottom morphisms, respectively. Now the statement that the squares are homotopy pullbacks is equivalent to their top left vertical morphisms being weak equivalences. Factor these top left morphisms functorially as cofibrations followed by acyclic fibrations. Then the statement that the squares are homotopy pullbacks is equivalent to those top left cofibrations being acyclic. Now the claim follows using that the retract of an acyclic cofibration is an acyclic cofibration (prop. ).
Long fiber sequences
The ordinary fiber, example , of a morphism has the property that taking it twice is always trivial:
This is crucially different for the homotopy fiber, def. . Here we discuss how this comes about and what the consequences are.
Proposition
Let be a category of fibrant objects of a model category, def. and let be a morphism in its category of pointed objects, def. . Then the homotopy fiber of its homotopy fiber, def. , is isomorphic, in , to the loop space object of (def. , prop. ):
Proof
Assume without restriction that is already a fibration between fibrant objects in (otherwise replace and rename). Then its homotopy fiber is its ordinary fiber, sitting in a pullback square
In order to compute , i.e. , we need to replace the fiber inclusion by a fibration. Using the factorization lemma for this purpose yields, after a choice of path space object (def. ), a replacement of the form
Hence is the ordinary fiber of this map:
Notice that
because of the pasting law:
Hence
Now we claim that there is a choice of path space objects and such that this model for the homotopy fiber (as an object in ) sits in a pullback diagram of the following form:
By the pasting law and the pullback stability of acyclic fibrations, this will prove the claim.
To see that the bottom square here is indeed a pullback, check the universal property: A morphism out of any into is a morphism and a morphism such that , and . Hence it is equivalently just a morphism such that and . This is the defining universal property of .
Now to construct the right vertical morphism in the top square (Quillen 67, page 3.1): Let be any path space object for and let be given by a factorization
and regarded as a path space object of by further comoposing with
We need to show that is an acyclic fibration.
It is a fibration because is a fibration, this being the pullback of the fibration .
To see that it is also a weak equivalence, first observe that , this being the pullback of the acyclic fibration of lemma . Hence we have a factorization of the identity as
and so finally the claim follows by two-out-of-three (def. ).
Remark
There is a conceptual way to understand prop. as follows: If we draw double arrows to indicate homotopies, then a homotopy fiber (def. ) is depicted by the following filled square:
just like the ordinary fiber (example ) is given by a plain square
One may show that just like the fiber is the universal solution to making such a commuting square (a pullback limit cone def. ), so the homotopy fiber is the universal solution up to homotopy to make such a commuting square up to homotopy – a homotopy pullback homotopy limit cone.
Now just like ordinary pullbacks satisfy the pasting law saying that attaching two pullback squares gives a pullback rectangle, the analogue is true for homotopy pullbacks. This implies that if we take the homotopy fiber of a homotopy fiber, thereby producing this double homotopy pullback square
then the total outer rectangle here is itself a homotopy pullback. But the outer rectangle exhibits the homotopy fiber of the point inclusion, which, via def. and lemma , is the loop space object:
Proposition
(long homotopy fiber sequences)
Let be a model category and let be morphism in the pointed homotopy category (prop. ). Then:
-
There is a long sequence to the left in of the form
where each morphism is the homotopy fiber (def. ) of the following one: the homotopy fiber sequence of . Here denotes followed by forming inverses with respect to the group structure on from prop. .
Moreover, for any object, then there is a long exact sequence
of pointed sets, where denotes the pointed set valued hom-functor of example .
-
Dually, there is a long sequence to the right in of the form
where each morphism is the homotopy cofiber (def. ) of the previous one: the homotopy cofiber sequence of . Moreover, for any object, then there is a long exact sequence
of pointed sets, where denotes the pointed set valued hom-functor of example .
Proof
That there are long sequences of this form is the result of combining prop. and prop. .
It only remains to see that it is indeed the morphisms that appear, as indicated.
In order to see this, it is convenient to adopt the following notation: for a morphism, then we denote the collection of generalized element of its homotopy fiber as
indicating that these elements are pairs consisting of an element of and a “path” (an element of the given path space object) from to the basepoint.
This way the canonical map is . Hence in this notation the homotopy fiber of the homotopy fiber reads
This identifies with by forming the loops
where the overline denotes reversal and the dot denotes concatenation.
Then consider the next homotopy fiber
where on the right we have a path in from to the basepoint element. This is a path together with a path-of-paths which connects to .
By the above convention this is identified with the loop in which is
But the map to sends this data to , hence to the loop
hence to the reveral of the image under of the loop in .
Remark
In (Quillen 67, I.3, prop. 3, prop. 4) more is shown than stated in prop. : there the connecting homomorphism is not just shown to exist, but is described in detail via an action of on in . This takes a good bit more work. For our purposes here, however, it is sufficient to know that such a morphism exists at all, hence that .
Example
Let be the classical model structure on topological spaces (compactly generated) from theorem , theorem . Then using the standard pointed topological path space objects from def. and example as the abstract path space objects in def. , via prop. , this gives that
is the th homotopy group, def. , of at its basepoint.
Hence using in the first item of prop. , the long exact sequence this gives is of the form
This is called the long exact sequence of homotopy groups induced by .
Remark
As we pass to stable homotopy theory (in Part 1)), the long exact sequences in example become long not just to the left, but also to the right. Given then a tower of fibrations, there is an induced sequence of such long exact sequences of homotopy groups, which organizes into an exact couple. For more on this see at Interlude – Spectral sequences (this remark).
Example
Let again be the classical model structure on topological spaces (compactly generated) from theorem , theorem , as in example . For any pointed topological space and an inclusion of pointed topological spaces, the exactness of the sequence in the second item of prop.
gives that the functor
behaves like one degree in an additive reduced cohomology theory (def.). The Brown representability theorem (thm.) implies that all additive reduced cohomology theories are degreewise representable this way (prop.).
-Groupoids I): Topological homotopy theory
This section first recalls relevant concepts from actual topology (“point-set topology”) and highlights facts that motivate the axiomatics of model categories below. We prove two technical lemmas (lemma and lemma ) that serve to establish the abstract homotopy theory of topological spaces further below.
Then we discuss how the category Top of topological spaces satisfies the axioms of abstract homotopy theory (model category) theory, def. .
Literature (Hirschhorn 15)
Throughout, let Top denote the category whose objects are topological spaces and whose morphisms are continuous functions between them. Its isomorphisms are the homeomorphisms.
(Further below we restrict attention to the full subcategory of compactly generated topological spaces.)
Universal constructions
To begin with, we recall some basics on universal constructions in Top: limits and colimits of diagrams of topological spaces; exponential objects.
We now discuss limits and colimits (Def. ) in Top. The key for understanding these is the fact that there are initial and final topologies:
Definition
Let be a set of topological spaces, and let be a bare set. Then
-
For a set of functions out of , the initial topology is the topology on with the minimum collection of open subsets such that all are continuous.
-
For a set of functions into , the final topology is the topology on with the maximum collection of open subsets such that all are continuous.
Example
For a single topological space, and a subset of its underlying set, then the initial topology , def. , is the subspace topology, making
a topological subspace inclusion.
Example
Conversely, for an epimorphism, then the final topology on is the quotient topology.
Proposition
Let be a small category and let be an -diagram in Top (a functor from to ), with components denoted , where and a topology on . Then:
-
The limit of exists and is given by the topological space whose underlying set is the limit in Set of the underlying sets in the diagram, and whose topology is the initial topology, def. , for the functions which are the limiting cone components:
Hence
-
The colimit of exists and is the topological space whose underlying set is the colimit in Set of the underlying diagram of sets, and whose topology is the final topology, def. for the component maps of the colimiting cocone
Hence
(e.g. Bourbaki 71, section I.4)
Proof
The required universal property of (def. ) is immediate: for
any cone over the diagram, then by construction there is a unique function of underlying sets making the required diagrams commute, and so all that is required is that this unique function is always continuous. But this is precisely what the initial topology ensures.
The case of the colimit is formally dual.
Example
The limit over the empty diagram in is the point with its unique topology.
Example
For a set of topological spaces, their coproduct is their disjoint union.
In particular:
Example
For , the -indexed coproduct of the point, is the set itself equipped with the final topology, hence is the discrete topological space on .
Example
For a set of topological spaces, their product is the Cartesian product of the underlying sets equipped with the product topology, also called the Tychonoff product.
In the case that is a finite set, such as for binary product spaces , then a sub-basis for the product topology is given by the Cartesian products of the open subsets of (a basis for) each factor space.
Example
The equalizer of two continuous functions in is the equalizer of the underlying functions of sets
(hence the largets subset of on which both functions coincide) and equipped with the subspace topology, example .
Example
The coequalizer of two continuous functions in is the coequalizer of the underlying functions of sets
(hence the quotient set by the equivalence relation generated by for all ) and equipped with the quotient topology, example .
Example
For
two continuous functions out of the same domain, then the colimit under this diagram is also called the pushout, denoted
(Here is also called the pushout of , or the cobase change of along .)
This is equivalently the coequalizer of the two morphisms from to the coproduct of with (example ):
If is an inclusion, one also writes and calls this the attaching space.
By example the pushout/attaching space is the quotient topological space
of the disjoint union of and subject to the equivalence relation which identifies a point in with a point in if they have the same pre-image in .
(graphics from Aguilar-Gitler-Prieto 02)
Notice that the defining universal property of this colimit means that completing the span
to a commuting square
is equivalent to finding a morphism
Example
For a topological subspace inclusion, example , then the pushout
is the quotient space or cofiber, denoted .
Example
An important special case of example :
For write
-
for the standard topological n-disk (equipped with its subspace topology as a subset of Cartesian space);
Notice that and that .
Let
be the canonical inclusion of the standard (n-1)-sphere as the boundary of the standard n-disk (both regarded as topological spaces with their subspace topology as subspaces of the Cartesian space ).
Then the colimit in Top under the diagram
i.e. the pushout of along itself, is the n-sphere :
(graphics from Ueno-Shiga-Morita 95)
Another kind of colimit that will play a role for certain technical constructions is transfinite composition. First recall
Definition
A partial order is a set equipped with a relation such that for all elements
1) (reflexivity) ;
2) (transitivity) if and then ;
3) (antisymmetry) if and then .
This we may and will equivalently think of as a category with objects the elements of and a unique morphism precisely if . In particular an order-preserving function between partially ordered sets is equivalently a functor between their corresponding categories.
A bottom element in a partial order is one such that for all a. A top element is one for wich .
A partial order is a total order if in addition
4) (totality) either or .
A total order is a well order if in addition
5) (well-foundedness) every non-empty subset has a least element.
An ordinal is the equivalence class of a well-order.
The successor of an ordinal is the class of the well-order with a top element freely adjoined.
A limit ordinal is one that is not a successor.
Example
The finite ordinals are labeled by , corresponding to the well-orders . Here is the successor of . The first non-empty limit ordinal is .
Definition
Let be a category, and let be a class of its morphisms.
For an ordinal (regarded as a category), an -indexed transfinite sequence of elements in is a diagram
such that
-
takes all successor morphisms in to elements in
-
is continuous in that for every nonzero limit ordinal , restricted to the full-subdiagram is a colimiting cocone in for restricted to .
The corresponding transfinite composition is the induced morphism
into the colimit of the diagram, schematically:
We now turn to the discussion of mapping spaces/exponential objects.
Definition
For a topological space and a locally compact topological space (in that for every point, every neighbourhood contains a compact neighbourhood), the mapping space
is the topological space
-
whose underlying set is the set of continuous functions ,
-
whose open subsets are unions of finitary intersections of the following subbase elements of standard open subsets:
the standard open subset for
-
a compact topological space subset
-
an open subset
is the subset of all those continuous functions that fit into a commuting diagram of the form
-
Accordingly this is called the compact-open topology on the set of functions.
The construction extends to a functor
Proposition
For a topological space and a locally compact topological space (in that for each point, each open neighbourhood contains a compact neighbourhood), the topological mapping space from def. is an exponential object, i.e. the functor is right adjoint to the product functor : there is a natural bijection
between continuous functions out of any product topological space of with any and continuous functions from into the mapping space.
A proof is spelled out here (or see e.g. Aguilar-Gitler-Prieto 02, prop. 1.3.1).
Remark
In the context of prop. it is often assumed that is also a Hausdorff topological space. But this is not necessary. What assuming Hausdorffness only achieves is that all alternative definitions of “locally compact” become equivalent to the one that is needed for the proposition: for every point, every open neighbourhood contains a compact neighbourhood.
Remark
Proposition fails in general if is not locally compact. Therefore the plain category Top of all topological spaces is not a Cartesian closed category.
This is no problem for the construction of the homotopy theory of topological spaces as such, but it becomes a technical nuisance for various constructions that one would like to perform within that homotopy theory. For instance on general pointed topological spaces the smash product is in general not associative.
On the other hand, without changing any of the following discussion one may just pass to a more convenient category of topological spaces such as notably the full subcategory of compactly generated topological spaces (def. ) which is Cartesian closed. This we turn to below.
Homotopy
The fundamental concept of homotopy theory is clearly that of homotopy. In the context of topological spaces this is about contiunous deformations of continuous functions parameterized by the standard interval:
Definition
Write
for the standard topological interval, a compact connected topological subspace of the real line.
Equipped with the canonical inclusion of its two endpoints
this is the standard interval object in Top.
For , the product topological space , example , is called the standard cylinder object over . The endpoint inclusions of the interval make it factor the codiagonal on
Definition
For two continuous functions between topological spaces , then a left homotopy
is a continuous function
out of the standard cylinder object over , def. , such that this fits into a commuting diagram of the form
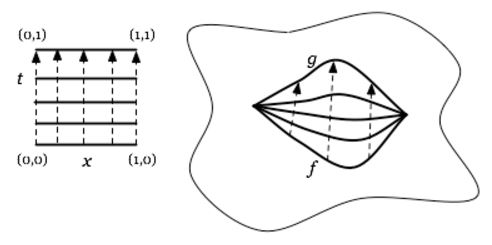
(graphics grabbed from J. Tauber here)
Example
Let be a topological space and let be two of its points, regarded as functions from the point to . Then a left homotopy, def. , between these two functions is a commuting diagram of the form
This is simply a continuous path in whose endpoints are and .
For instance:
Example
Let
be the continuous function from the standard interval to itself that is constant on the value 0. Then there is a left homotopy, def. , from the identity function
given by
A key application of the concept of left homotopy is to the definition of homotopy groups:
Definition
For a topological space, then its set of connected components, also called the 0-th homotopy set, is the set of left homotopy-equivalence classes (def. ) of points , hence the set of path-connected components of (example ). By composition this extends to a functor
For , and for any point, then the th homotopy group of at is the group
-
whose underlying set is the set of left homotopy-equivalence classes of maps that take the boundary of to and where the left homotopies are constrained to be constant on the boundary;
-
whose group product operation takes and to with
where the first map is a homeomorphism from the unit -cube to the -cube with one side twice the unit length (e.g. ).
By composition, this construction extends to a functor
from pointed topological spaces to graded groups.
Notice that often one writes the value of this functor on a morphism as .
Remark
At this point we don’t go further into the abstract reason why def. yields group structure above degree 0, which is that positive dimension spheres are H-cogroup objects. But this is important, for instance in the proof of the Brown representability theorem. See the section Brown representability theorem in Part S.
Definition
A continuous function is called a homotopy equivalence if there exists a continuous function the other way around, , and left homotopies, def. , from the two composites to the identity:
and
If here is constant along , is said to exhibit as a deformation retract of .
Example
For a topological space and its standard cylinder object of def. , then the projection and the inclusion are homotopy equivalences, def. , and in fact are homotopy inverses to each other:
The composition
is immediately the identity on (i.e. homotopic to the identity by a trivial homotopy), while the composite
is homotopic to the identity on by a homotopy that is pointwise in that of example .
Definition
A continuous function is called a weak homotopy equivalence if its image under all the homotopy group functors of def. is an isomorphism, hence if
and for all and all
Proposition
Every homotopy equivalence, def. , is a weak homotopy equivalence, def. .
In particular a deformation retraction, def. , is a weak homotopy equivalence.
Proof
First observe that for all Top the inclusion maps
into the standard cylinder object, def. , are weak homotopy equivalences: by postcomposition with the contracting homotopy of the interval from example all homotopy groups of have representatives that factor through this inclusion.
Then given a general homotopy equivalence, apply the homotopy groups functor to the corresponding homotopy diagrams (where for the moment we notationally suppress the choice of basepoint for readability) to get two commuting diagrams
By the previous observation, the vertical morphisms here are isomorphisms, and hence these diagrams exhibit as the inverse of , hence both as isomorphisms.
Remark
The converse of prop. is not true generally: not every weak homotopy equivalence between topological spaces is a homotopy equivalence. (For an example with full details spelled out see for instance Fritsch, Piccinini: “Cellular Structures in Topology”, p. 289-290).
However, as we will discuss below, it turns out that
-
every weak homotopy equivalence between CW-complexes is a homotopy equivalence (Whitehead's theorem, cor. );
-
every topological space is connected by a weak homotopy equivalence to a CW-complex (CW approximation, remark ).
Example
For , the projection from the cylinder object of , def. , is a weak homotopy equivalence, def. . This means that the factorization
of the codiagonal in def. , which in general is far from being a monomorphism, may be thought of as factoring it through a monomorphism after replacing , up to weak homotopy equivalence, by .
In fact, further below (prop. ) we see that has better properties than the generic monomorphism has, in particular better homotopy invariant properties: it has the left lifting property against all Serre fibrations that are also weak homotopy equivalences.
Of course the concept of left homotopy in def. is accompanied by a concept of right homotopy. This we turn to now.
Definition
For a topological space, its standard topological path space object is the topological path space, hence the mapping space , prop. , out of the standard interval of def. .
Example
The endpoint inclusion into the standard interval, def. , makes the path space of def. factor the diagonal on through the inclusion of constant paths and the endpoint evaluation of paths:
This is the formal dual to example . As in that example, below we will see (prop. ) that this factorization has good properties, in that
-
is a Serre fibration.
So while in general the diagonal is far from being an epimorphism or even just a Serre fibration, the factorization through the path space object may be thought of as replacing , up to weak homotopy equivalence, by its path space, such as to turn its diagonal into a Serre fibration after all.
Definition
For two continuous functions between topological spaces , then a right homotopy is a continuous function
into the path space object of , def. , such that this fits into a commuting diagram of the form
Cell complexes
We consider topological spaces that are built consecutively by attaching basic cells.
Definition
Write
for the set of canonical boundary inclusion maps of the standard n-disks, example . This going to be called the set of standard topological generating cofibrations.
Definition
For and for , an -cell attachment to is the pushout (“attaching space”, example ) of a generating cofibration, def.
along some continuous function .
A continuous function is called a topological relative cell complex if it is exhibited by a (possibly infinite) sequence of cell attachments to , in that it is a transfinite composition (def. ) of pushouts (example )
of coproducts (example ) of generating cofibrations (def. ).
A topological space is a cell complex if is a relative cell complex.
A relative cell complex is called a finite relative cell complex if it is obtained from a finite number of cell attachments.
A (relative) cell complex is called a (relative) CW-complex if the above transfinite composition is countable
and if is obtained from by attaching cells precisely only of dimension .
Remark
Strictly speaking a relative cell complex, def. , is a function , together with its cell structure, hence together with the information of the pushout diagrams and the transfinite composition of the pushout maps that exhibit it.
In many applications, however, all that matters is that there is some (relative) cell decomosition, and then one tends to speak loosely and mean by a (relative) cell complex only a (relative) topological space that admits some cell decomposition.
The following lemma , together with lemma below are the only two statements of the entire development here that involve the concrete particular nature of topological spaces (“point-set topology”), everything beyond that is general abstract homotopy theory.
Lemma
Assuming the axiom of choice and the law of excluded middle, every compact subspace of a topological cell complex, def. , intersects the interior of a finite number of cells.
(e.g. Hirschhorn 15, section 3.1)
Proof
So let be a topological cell complex and a compact subspace. Define a subset
by choosing one point in the interior of the intersection with of each cell of that intersects .
It is now sufficient to show that has no accumulation point. Because, by the compactness of , every non-finite subset of does have an accumulation point, and hence the lack of such shows that is a finite set and hence that intersects the interior of finitely many cells of .
To that end, let be any point. If is a 0-cell in , write . Otherwise write for the unique cell of that contains in its interior. By construction, there is exactly one point of in the interior of . Hence there is an open neighbourhood containing no further points of beyond possibly itself, if happens to be that single point of in .
It is now sufficient to show that may be enlarged to an open subset of containing no point of , except for possibly itself, for that means that is not an accumulation point of .
To that end, let be the ordinal that labels the stage of the transfinite composition in the cell complex-presentation of at which the cell above appears. Let be the ordinal of the full cell complex. Then define the set
and regard this as a partially ordered set by declaring a partial ordering via
This is set up such that every element of with the maximum value is an extension that we are after.
Observe then that for a chain in (a subset on which the relation restricts to a total order), it has an upper bound in given by the union . Therefore Zorn's lemma applies, saying that contains a maximal element .
Hence it is now sufficient to show that . We argue this by showing that assuming leads to a contradiction.
So assume . Then to construct an element of that is larger than , consider for each cell at stage its attaching map and the corresponding preimage open set . Enlarging all these preimages to open subsets of (such that their image back in does not contain ), then . This is a contradiction. Hence , and we are done.
It is immediate and useful to generalize the concept of topological cell complexes as follows.
Definition
For any category and for any sub-class of its morphisms, a relative -cell complexes is a morphism in which is a transfinite composition (def. ) of pushouts of coproducts of morphsims in .
Definition
Write
for the set of inclusions of the topological n-disks, def. , into their cylinder objects, def. , along (for definiteness) the left endpoint inclusion.
These inclusions are similar to the standard topological generating cofibrations of def. , but in contrast to these they are “acyclic” (meaning: trivial on homotopy classes of maps from “cycles” given by n-spheres) in that they are weak homotopy equivalences (by prop. ).
Accordingly, is to be called the set of standard topological generating acyclic cofibrations.
Lemma
For a CW-complex (def. ), then its inclusion into its standard cylinder (def. ) is a -relative cell complex (def. , def. ).
Proof
First erect a cylinder over all 0-cells
Assume then that the cylinder over all -cells of has been erected using attachment from . Then the union of any -cell of with the cylinder over its boundary is homeomorphic to and is like the cylinder over the cell “with end and interior removed”. Hence via attaching along the cylinder over is erected.
Lemma
The maps in def. are finite relative cell complexes, def. . In other words, the elements of are -relative cell complexes.
Proof
There is a homeomorphism
such that the map on the right is the inclusion of one hemisphere into the boundary n-sphere of . This inclusion is the result of attaching two cells:
Lemma
Every -relative cell complex (def. , def. ) is a weak homotopy equivalence, def. .
Proof
Let be a -relative cell complex.
First observe that with the elements of being homotopy equivalences for all (by example ), each of the stages in the relative cell complex is also a homotopy equivalence. We make this fully explicit:
By definition, such a stage is a pushout of the form
Then the fact that the projections are strict left inverses to the inclusions gives a commuting square of the form
and so the universal property of the colimit (pushout) gives a factorization of the identity morphism on the right through
which exhibits as a strict left inverse to . Hence it is now sufficient to show that this is also a homotopy right inverse.
To that end, let
be the left homotopy that exhibits as a homotopy right inverse to by example . For each consider the commuting square
Regarded as a cocone under the span in the top left, the universal property of the colimit (pushout) gives a continuous function
for each . For this construction reduces to the provious one in that is the composite which we need to homotope to the identity; while is the identity. Since is clearly also continuous in it constitutes a continuous function
which exhibits the required left homotopy.
So far this shows that each stage in the transfinite composition defining is a homotopy equivalence, hence, by prop. , a weak homotopy equivalence.
This means that all morphisms in the following diagram (notationally suppressing basepoints and showing only the finite stages)
are isomorphisms.
Moreover, lemma gives that every representative and every null homotopy of elements in already exists at some finite stage . This means that also the universally induced morphism
is an isomorphism. Hence the composite is an isomorphism.
Fibrations
Given a relative -cell complex , def. , it is typically interesting to study the extension problem along , i.e. to ask which topological spaces are such that every continuous function has an extension along
If such extensions exists, it means that is sufficiently “spread out” with respect to the maps in . More generally one considers this extension problem fiberwise, i.e. with both and (hence also ) equipped with a map to some base space :
Definition
Given a category and a sub-class of its morphisms, then a morphism in is said to have the right lifting property against the morphisms in if every commuting diagram in of the form
with , has a lift , in that it may be completed to a commuting diagram of the form
We will also say that is a -injective morphism if it satisfies the right lifting property against .
Definition
A continuous function is called a Serre fibration if it is a -injective morphism; i.e. if it has the right lifting property, def. , against all topological generating acylic cofibrations, def. ; hence if for every commuting diagram of continuous functions of the form
has a lift , in that it may be completed to a commuting diagram of the form
Remark
Def. says, in view of the definition of left homotopy, that a Serre fibration is a map with the property that given a left homotopy, def. , between two functions into its codomain, and given a lift of one the two functions through , then also the homotopy between the two lifts. Therefore the condition on a Serre fibration is also called the homotopy lifting property for maps whose domain is an n-disk.
More generally one may ask functions to have such homotopy lifting property for functions with arbitrary domain. These are called Hurewicz fibrations.
Remark
The precise shape of and in def. turns out not to actually matter much for the nature of Serre fibrations. We will eventually find below (prop. ) that what actually matters here is only that the inclusions are relative cell complexes (lemma ) and weak homotopy equivalences (prop. ) and that all of these may be generated from them in a suitable way.
But for simple special cases this is readily seen directly, too. Notably we could replace the n-disks in def. with any homeomorphic topological space. A choice important in the comparison to the classical model structure on simplicial sets (below) is to instead take the topological n-simplices . Hence a Serre fibration is equivalently characterized as having lifts in all diagrams of the form
Other deformations of the -disks are useful in computations, too. For instance there is a homeomorphism from the -disk to its “cylinder with interior and end removed”, formally:
and hence is a Serre fibration equivalently also if it admits lifts in all diagrams of the form
The following is a general fact about closure of morphisms defined by lifting properties which we prove in generality below as prop. .
Proposition
A Serre fibration, def. has the right lifting property against all retracts (see remark ) of -relative cell complexes (def. , def. ).
The following statement is foreshadowing the long exact sequences of homotopy groups (below) induced by any fiber sequence, the full version of which we come to below (example ) after having developed more of the abstract homotopy theory.
Proposition
Let be a Serre fibration, def. , let be any point and write
for the fiber inclusion over that point. Then for every choice of lift of the point through , the induced sequence of homotopy groups
is exact, in that the kernel of is canonically identified with the image of :
Proof
It is clear that the image of is in the kernel of (every sphere in becomes constant on , hence contractible, when sent forward to ).
For the converse, let be represented by some . Assume that is in the kernel of . This means equivalently that fits into a commuting diagram of the form
where is the contracting homotopy witnessing that .
Now since is a lift of , there exists a left homotopy
as follows:
(for instance: regard as embedded in such that is identified with the basepoint on the boundary of and set ).
The pasting of the top two squares that have appeared this way is equivalent to the following commuting square
Because is a Serre fibration and by lemma and prop. , this has a lift
Notice that is a basepoint preserving left homotopy from to some . Being homotopic, they represent the same element of :
But the new representative has the special property that its image in is not just trivializable, but trivialized: combining with the previous diagram shows that it sits in the following commuting diagram
The commutativity of the outer square says that is constant, hence that is entirely contained in the fiber . Said more abstractly, the universal property of fibers gives that factors through , hence that is in the image of .
The following lemma , together with lemma above, are the only two statements of the entire development here that crucially involve the concrete particular nature of topological spaces (“point-set topology”), everything beyond that is general abstract homotopy theory.
Lemma
The continuous functions with the right lifting property, def. against the set of topological generating cofibrations, def. , are precisely those which are both weak homotopy equivalences, def. as well as Serre fibrations, def. .
Proof
We break this up into three sub-statements:
A) -injective morphisms are in particular weak homotopy equivalences
Let have the right lifting property against
We check that the lifts in these diagrams exhibit as being an isomorphism on all homotopy groups, def. :
For the existence of these lifts says that every point of is in the image of , hence that is surjective. Let then be a map that hits two connected components, then the existence of the lift says that if they have the same image in then they were already the same connected component in . Hence is also injective and hence is a bijection.
Similarly, for , if represents an element in that becomes trivial in , then the existence of the lift says that it already represented the trivial element itself. Hence has trivial kernel and so is injective.
Finally, to see that is also surjective, hence bijective, observe that every elements in is equivalently represented by a commuting diagram of the form
and so here the lift gives a representative of a preimage in .
B) -injective morphisms are in particular Serre fibrations
By an immediate closure property of lifting problems (we spell this out in generality as prop. , cor. below) an -injective morphism has the right lifting property against all relative cell complexes, and hence, by lemma , it is also a -injective morphism, hence a Serre fibration.
C) Acyclic Serre fibrations are in particular -injective morphisms
Let be a Serre fibration that induces isomorphisms on homotopy groups. In degree 0 this means that is an isomorphism on connected components, and this means that there is a lift in every commuting square of the form
(this is being surjective) and in every commuting square of the form
(this is being injective). Hence we are reduced to showing that for every diagram of the form
has a lift.
To that end, pick a basepoint on and write and for its images in and , respectively
Then the diagram above expresses that and hence by assumption on it follows that , which in turn mean that there is making the upper triangle of our lifting problem commute:
It is now sufficient to show that any such may be deformed to a which keeps making this upper triangle commute but also makes the remaining lower triangle commute.
To that end, notice that by the commutativity of the original square, we already have at least this commuting square:
This induces the universal map from the pushout of its cospan in the top left, which is the n-sphere (see this example):
This universal morphism represents an element of the th homotopy group:
By assumption that is a weak homotopy equivalence, there is a with
hence on representatives there is a lift up to homotopy
Morever, we may always find of the form for some . (“Paste to the reverse of .”)
Consider then the map
and observe that this represents the trivial class:
This means equivalently that there is a homotopy
fixing the boundary of the -disk.
Hence if we denote homotopy by double arrows, then we have now achieved the following situation
and it now suffices to show that may be lifted to a homotopy of just , fixing the boundary, for then the resulting homotopic is the desired lift.
To that end, notice that the condition that fixes the boundary of the -disk means equivalently that it extends to a morphism
out of the pushout that identifies in the cylinder over all points lying over the boundary. Hence we are reduced to finding a lift in
But inspection of the left map reveals that it is homeomorphic again to , and hence the lift does indeed exist.
The classical model structure on topological spaces
Definition
Say that a continuous function, hence a morphism in Top, is
-
a classical weak equivalence if it is a weak homotopy equivalence, def. ;
-
a classical fibration if it is a Serre fibration, def. ;
-
a classical cofibration if it is a retract (rem. ) of a relative cell complex, def. .
and hence
-
a acyclic classical cofibration if it is a classical cofibration as well as a classical weak equivalence;
-
a acyclic classical fibration if it is a classical fibration as well as a classical weak equivalence.
Write
for the classes of these morphisms, respectively.
We first prove now that the classes of morphisms in def. satisfy the conditions for a model category structure, def. (after some lemmas, this is theorem below). Then we discuss the resulting classical homotopy category (below) and then a few variant model structures whose proof follows immediately along the line of the proof of :
-
The model structure on compactly generated topological spaces and ;
-
The model structure on topologically enriched functors and .
Proposition
The classical weak equivalences, def. , satify two-out-of-three (def. ).
Proof
Since isomorphisms (of homotopy groups) satisfy 2-out-of-3, this property is directly inherited via the very definition of weak homotopy equivalence, def. .
Lemma
Every morphism in Top factors as a classical cofibration followed by an acyclic classical fibration, def. :
Proof
By lemma the set of topological generating cofibrations, def. , has small domains, in the sense of def. (the n-spheres are compact). Hence by the small object argument, prop. , factors as an -relative cell complex, def. , hence just a plain relative cell complex, def. , followed by an -injective morphisms, def. :
By lemma the map is both a weak homotopy equivalence as well as a Serre fibration.
Lemma
Every morphism in Top factors as an acyclic classical cofibration followed by a fibration, def. :
Proof
By lemma the set of topological generating acyclic cofibrations, def. , has small domains, in the sense of def. (the n-disks are compact). Hence by the small object argument, prop. , factors as an -relative cell complex, def. , followed by a -injective morphisms, def. :
By definition this makes a Serre fibration, hence a fibration.
By lemma a relative -cell complex is in particular a relative -cell complex. Hence is a classical cofibration. By lemma it is also a weak homotopy equivalence, hence a clasical weak equivalence.
Lemma
Every commuting square in Top with the left morphism a classical cofibration and the right morphism a fibration, def.
admits a lift as soon as one of the two is also a classical weak equivalence.
Proof
A) If the fibration is also a weak equivalence, then lemma says that it has the right lifting property against the generating cofibrations , and cor. implies the claim.
B) If the cofibration on the left is also a weak equivalence, consider any factorization into a relative -cell complex, def. , def. , followed by a fibration,
as in the proof of lemma . By lemma the morphism is a weak homotopy equivalence, and so by two-out-of-three (prop. ) the factorizing fibration is actually an acyclic fibration. By case A), this acyclic fibration has the right lifting property against the cofibration itself, and so the retract argument, lemma gives that is a retract of a relative -cell complex. With this, finally cor. implies that has the right lifting property against .
Finally:
Proposition
The systems and from def. are weak factorization systems.
Proof
Since we have already seen the factorization property (lemma , lemma ) and the lifting properties (lemma ), it only remains to see that the given left/right classes exhaust the class of morphisms with the given lifting property.
For the classical fibrations this is by definition, for the the classical acyclic fibrations this is by lemma .
The remaining statement for and follows from a general argument (here) for cofibrantly generated model categories (def. ), which we spell out:
So let be in , we need to show that then is a retract (remark ) of a relative cell complex. To that end, apply the small object argument as in lemma to factor as
It follows that has the left lifting property against , and hence by the retract argument (lemma ) it is a retract of . This proves the claim for .
The analogous argument for , using the small object argument for , shows that every is a retract of a -cell complex. By lemma and lemma a -cell complex is both an -cell complex and a weak homotopy equivalence. Retracts of the former are cofibrations by definition, and retracts of the latter are still weak homotopy equivalences by lemma . Hence such is an acyclic cofibration.
In conclusion, prop. and prop. say that:
Theorem
The classes of morphisms in of def. ,
define a model category structure (def. ) , the classical model structure on topological spaces or Serre-Quillen model structure .
In particular
-
every object in is fibrant;
-
the cofibrant objects in are the retracts of cell complexes.
Hence in particular the following classical statement is an immediate corollary:
Corollary
(Whitehead theorem)
Every weak homotopy equivalence (def. ) between topological spaces that are homeomorphic to a retract of a cell complex, in particular to a CW-complex (def. ), is a homotopy equivalence (def. ).
In proving theorem we have in fact shown a bit more that stated. Looking back, all the structure of is entirely induced by the set (def. ) of generating cofibrations and the set (def. ) of generating acyclic cofibrations (whence the terminology). This situation is usefully summarized by the concept of cofibrantly generated model category (Def. ).
This phenomenon will keep recurring and will keep being useful as we construct further model categories, such as the classical model structure on pointed topological spaces (def. ), the projective model structure on topological functors (thm. ), and finally various model structures on spectra which we turn to in the section on stable homotopy theory.
The classical homotopy category
With the classical model structure on topological spaces in hand, we now have good control over the classical homotopy category:
Definition
The Serre-Quillen classical homotopy category is the homotopy category, def. , of the classical model structure on topological spaces from theorem : we write
Remark
From just theorem , the definition (def. ) gives that
is the category whose objects are retracts of cell complexes (def. ) and whose morphisms are homotopy classes of continuous functions. But in fact more is true:
Theorem in itself implies that every topological space is weakly equivalent to a retract of a cell complex, def. . But by the existence of CW approximations, this cell complex may even be taken to be a CW complex.
(Better yet, there is Quillen equivalence to the classical model structure on simplicial sets which implies a functorial CW approximation given by forming the geometric realization of the singular simplicial complex of .)
Hence the Serre-Quillen classical homotopy category is also equivalently the category of just the CW-complexes whith homotopy classes of continuous functions between them
It follows that the universal property of the homotopy category (theorem )
implies that there is a bijection, up to natural isomorphism, between
-
functors out of which agree on homotopy-equivalent maps;
-
functors out of all of which send weak homotopy equivalences to isomorphisms.
This statement in particular serves to show that two different axiomatizations of generalized (Eilenberg-Steenrod) cohomology theories are equivalent to each other. See at Introduction to Stable homotopy theory – S the section generalized cohomology functors (this prop.)
Beware that, by remark , what is not equivalent to is the category
obtained from all topological spaces with morphisms the homotopy classes of continuous functions. This category is “too large”, the correct homotopy category is just the genuine full subcategory
Beware also the ambiguity of terminology: “classical homotopy category” some literature refers to instead of . However, here we never have any use for and will not mention it again.
Proposition
Let be a CW-complex, def. . Then the standard topological cylinder of def.
(obtained by forming the product space with the standard topological interval ) is indeed a cylinder object in the abstract sense of def. .
Proof
We describe the proof informally. It is immediate how to turn this into a formal proof, but the notation becomes tedious. (One place where it is spelled out completely is Ottina 14, prop. 2.9.)
So let be a presentation of as a CW-complex. Proceed by induction on the cell dimension.
First observe that the cylinder over is a cell complex: First itself is a disjoint union of points. Adding a second copy for every point (i.e. attaching along ) yields , then attaching an inteval between any two corresponding points (along ) yields .
So assume that for it has been shown that has the structure of a CW-complex of dimension . Then for each cell of , attach it twice to , once at , and once at .
The result is with a hollow cylinder erected over each of its -cells. Now fill these hollow cylinders (along ) to obtain .
This completes the induction, hence the proof of the CW-structure on .
The construction also manifestly exhibits the inclusion as a relative cell complex.
Finally, it is clear (prop. ) that is a weak homotopy equivalence.
Conversely:
Proposition
Let be any topological space. Then the standard topological path space object (def. )
(obtained by forming the mapping space, def. , with the standard topological interval ) is indeed a path space object in the abstract sense of def. .
Proof
To see that is a weak homotopy equivalence it is sufficient, by prop. , to exhibit a homotopy equivalence. Let the homotopy inverse be . Then the composite
is already equal to the identity. The other we round, the rescaling of paths provides the required homotopy
To see that is a fibration, we need to show that every commuting square of the form
has a lift.
Now first use the adjunction from prop. to rewrite this equivalently as the following commuting square:
This square is equivalently (example ) a morphism out of the pushout
By the same reasoning, a lift in the original diagram is now equivalently a lifting in
Inspection of the component maps shows that the left vertical morphism here is the inclusion into the square times of three of its faces times . This is homeomorphic to the inclusion (as in remark ). Therefore a lift in this square exsists, and hence a lift in the original square exists.
Model structure on pointed spaces
A pointed object is of course an object equipped with a point , and a morphism of pointed objects is a morphism that takes to . Trivial as this is in itself, it is good to record some basic facts, which we do here.
Passing to pointed objects is also the first step in linearizing classical homotopy theory to stable homotopy theory. In particular, every category of pointed objects has a zero object, hence has zero morphisms. And crucially, if the original category had Cartesian products, then its pointed objects canonically inherit a non-cartesian tensor product: the smash product. These ingredients will be key below in the section on stable homotopy theory.
Definition
Let be a category and let be an object.
The slice category is the category whose
-
objects are morphisms in ;
-
morphisms are commuting triangles in .
Dually, the coslice category is the category whose
-
objects are morphisms in ;
-
morphisms are commuting triangles in .
There are the canonical forgetful functors
given by forgetting the morphisms to/from .
We here focus on this class of examples:
Definition
For a category with terminal object , the coslice category (def. ) is the corresponding category of pointed objects: its
-
objects are morphisms in of the form (hence an object equipped with a choice of point; i.e. a pointed object);
-
morphisms are commuting triangles of the form
(hence morphisms in which preserve the chosen points).
Remark
In a category of pointed objects , def. , the terminal object coincides with the initial object, both are given by itself, pointed in the unique way.
In this situation one says that is a zero object and that is a pointed category.
It follows that also all hom-sets of are canonically pointed sets, pointed by the zero morphism
Definition
Let be a category with terminal object and finite colimits. Then the forgetful functor from its category of pointed objects, def. , has a left adjoint
given by forming the disjoint union (coproduct) with a base point (“adjoining a base point”).
Proposition
Let be a category with all limits and colimits. Then also the category of pointed objects , def. , has all limits and colimits.
Moreover:
-
the limits are the limits of the underlying diagrams in , with the base point of the limit induced by its universal property in ;
-
the colimits are the limits in of the diagrams with the basepoint adjoined.
Proof
It is immediate to check the relevant universal property. For details see at slice category – limits and colimits.
Example
Given two pointed objects and , then:
-
their product in is simply ;
-
their coproduct in has to be computed using the second clause in prop. : since the point has to be adjoined to the diagram, it is given not by the coproduct in , but by the pushout in of the form:
This is called the wedge sum operation on pointed objects.
Generally for a set in
Example
For a CW-complex, def. then for every the quotient (example ) of its -skeleton by its -skeleton is the wedge sum, def. , of -spheres, one for each -cell of :
Definition
For a category of pointed objects with finite limits and finite colimits, the smash product is the functor
given by
hence by the pushout in
In terms of the wedge sum from def. , this may be written concisely as
Remark
For a general category in def. , the smash product need not be associative, namely it fails to be associative if the functor does not preserve the quotients involved in the definition.
In particular this may happen for Top.
A sufficient condition for to preserve quotients is that it is a left adjoint functor. This is the case in the smaller subcategory of compactly generated topological spaces, we come to this in prop. below.
These two operations are going to be ubiquituous in stable homotopy theory:
| symbol | name | category theory |
|---|---|---|
| wedge sum | coproduct in | |
| smash product | tensor product in |
Example
Let be pointed topological spaces. Then
denotes the standard interval object from def. , with a djoint basepoint adjoined, def. . Now for any pointed topological space, then
is the reduced cylinder over : the result of forming the ordinary cyclinder over as in def. , and then identifying the interval over the basepoint of with the point.
(Generally, any construction in properly adapted to pointed objects is called the “reduced” version of the unpointed construction. Notably so for “reduced suspension” which we come to below.)
Just like the ordinary cylinder receives a canonical injection from the coproduct formed in , so the reduced cyclinder receives a canonical injection from the coproduct formed in , which is the wedge sum from example :
Example
For pointed topological spaces with a locally compact topological space, then the pointed mapping space is the topological subspace of the mapping space of def.
on those maps which preserve the basepoints, and pointed by the map constant on the basepoint of .
In particular, the standard topological pointed path space object on some pointed (the pointed variant of def. ) is the pointed mapping space .
The pointed consequence of prop. then gives that there is a natural bijection
between basepoint-preserving continuous functions out of a smash product, def. , with pointed continuous functions of one variable into the pointed mapping space.
Example
Given a morphism in a category of pointed objects , def. , with finite limits and colimits,
Remark
In the situation of example , both the pullback as well as the pushout are equivalently computed in . For the pullback this is the first clause of prop. . The second clause says that for computing the pushout in , first the point is to be adjoined to the diagram, and then the colimit over the larger diagram
be computed. But one readily checks that in this special case this does not affect the result. (The technical jargon is that the inclusion of the smaller diagram into the larger one in this case happens to be a final functor.)
Proposition
Let be a model category and let be an object. Then both the slice category as well as the coslice category , def. , carry model structures themselves – the model structure on a (co-)slice category, where a morphism is a weak equivalence, fibration or cofibration iff its image under the forgetful functor is so in .
In particular the category of pointed objects, def. , in a model category becomes itself a model category this way.
The corresponding homotopy category of a model category, def. , we call the pointed homotopy category .
Proof
This is immediate:
By prop. the (co-)slice category has all limits and colimits. By definition of the weak equivalences in the (co-)slice, they satisfy two-out-of-three, def. , because the do in .
Similarly, the factorization and lifting is all induced by : Consider the coslice category , the case of the slice category is formally dual; then if
commutes in , and a factorization of exists in , it uniquely makes this diagram commute
Similarly, if
is a commuting diagram in , hence a commuting diagram in as shown, with all objects equipped with compatible morphisms from , then inspection shows that any lift in the diagram necessarily respects the maps from , too.
Example
For any model category, with its pointed model structure according to prop. , then the corresponding homotopy category (def. ) is, by remark , canonically enriched in pointed sets, in that its hom-functor is of the form
Definition
Write for the classical model structure on pointed topological spaces, obtained from the classical model structure on topological spaces (theorem ) via the induced coslice model structure of prop. .
Its homotopy category, def. ,
we call the classical pointed homotopy category.
Remark
The fibrant objects in the pointed model structure , prop. , are those that are fibrant as objects of . But the cofibrant objects in are now those for which the basepoint inclusion is a cofibration in .
For from def. , then the corresponding cofibrant pointed topological spaces are tyically referred to as spaces with non-degenerate basepoints or . Notice that the point itself is cofibrant in , so that cofibrant pointed topological spaces are in particular cofibrant topological spaces.
While the existence of the model structure on is immediate, via prop. , for the discussion of topologically enriched functors (below) it is useful to record that this, too, is a cofibrantly generated model category (def. ), as follows:
Definition
Write
and
respectively, for the sets of morphisms obtained from the classical generating cofibrations, def. , and the classical generating acyclic cofibrations, def. , under adjoining of basepoints (def. ).
Theorem
The sets and in def. exhibit the classical model structure on pointed topological spaces of def. as a cofibrantly generated model category, def. .
(This is also a special case of a general statement about cofibrant generation of coslice model structures, see this proposition.)
Proof
Due to the fact that in a basepoint is freely adjoined, lemma goes through verbatim for the pointed case, with replaced by , as do the other two lemmas above that depend on point-set topology, lemma and lemma . With this, the rest of the proof follows by the same general abstract reasoning as above in the proof of theorem .
Model structure on compactly generated spaces
The category Top has the technical inconvenience that mapping spaces (def. ) satisfying the exponential property (prop. ) exist in general only for a locally compact topological space, but fail to exist more generally. In other words: Top is not cartesian closed. But cartesian closure is necessary for some purposes of homotopy theory, for instance it ensures that
-
the smash product (def. ) on pointed topological spaces is associative (prop. below);
-
there is a concept of topologically enriched functors with values in topological spaces, to which we turn below;
-
geometric realization of simplicial sets preserves products.
The first two of these are crucial for the development of stable homotopy theory in the next section, the third is a great convenience in computations.
Now, since the homotopy theory of topological spaces only cares about the CW approximation to any topological space (remark ), it is plausible to ask for a full subcategory of Top which still contains all CW-complexes, still has all limits and colimits, still supports a model category structure constructed in the same way as above, but which in addition is cartesian closed, and preferably such that the model structure interacts well with the cartesian closure.
Such a full subcategory exists, the category of compactly generated topological spaces. This we briefly describe now.
Literature (Strickland 09)
Definition
Let be a topological space.
A subset is called compactly closed (or -closed) if for every continuous function out of a compact Hausdorff space , then the preimage is a closed subset of .
The space is called compactly generated if its closed subsets exhaust (hence coincide with) the -closed subsets.
Write
for the full subcategory of Top on the compactly generated topological spaces.
Definition
Write
for the functor which sends any topological space to the topological space with the same underlying set , but with open subsets the collection of all -open subsets with respect to .
Proof
We need to show that for a -closed subset, then the preimage is closed subset.
Let be any continuous function out of a compact Hausdorff space . Since is -closed by assumption, we have that is closed in . This means that is -closed in . But by the assumption that is compactly generated, it follows that is already closed.
Corollary
For there is a natural bijection
This means equivalently that the functor (def. ) together with the inclusion from def. forms an pair of adjoint functors
This in turn means equivalently that is a coreflective subcategory with coreflector . In particular is idemotent in that there are natural homeomorphisms
Hence colimits in exists and are computed as in Top. Also limits in exists, these are obtained by computing the limit in Top and then applying the functor to the result.
The following is a slight variant of def. , appropriate for the context of .
Definition
For (def. ) the compactly generated mapping space is the compactly generated topological space whose underlying set is the set of continuous functions , and for which a subbase for its topology has elements , for any open subset and a continuous function out of a compact Hausdorff space given by
Remark
If is (compactly generated and) a Hausdorff space, then the topology on the compactly generated mapping space in def. agrees with the compact-open topology of def. . Beware that it is common to say “compact-open topology” also for the topology of the compactly generated mapping space when is not Hausdorff. In that case, however, the two definitions in general disagree.
Proposition
The category of def. is cartesian closed:
for every then the operation of forming the Cartesian product in (which by cor. is applied to the usual product topological space) together with the operation of forming the compactly generated mapping space (def. ) forms a pair of adjoint functors
For proof see for instance (Strickland 09, prop. 2.12).
Corollary
For , the operation of forming the pointed mapping space (example ) inside the compactly generated mapping space of def.
is left adjoint to the smash product operation on pointed compactly generated topological spaces.
Corollary
For a small category and a diagram, then the compactly generated mapping space construction from def. preserves limits in its covariant argument and sends colimits in its contravariant argument to limits:
and
Proof
The first statement is an immediate implication of being a right adjoint, according to cor. .
For the second statement, we use that by def. a compactly generated topological space is uniquely determined if one knows all continuous functions out of compact Hausdorff spaces into it. Hence it is sufficient to show that there is a natural isomorphism
for any compact Hausdorff space.
With this, the statement follows by cor. and using that ordinary hom-sets take colimits in the first argument and limits in the second argument to limits:
Moreover, compact generation fixes the associativity of the smash product (remark ):
Proposition
On pointed (def. ) compactly generated topological spaces (def. ) the smash product (def. )
is associative and the 0-sphere is a tensor unit for it.
Proof
Since is a left adjoint by prop. , it presevers colimits and in particular quotient space projections. Therefore with then
The analogous reasoning applies to yield also .
Remark
Corollary together with prop. says that under the smash product the category of pointed compactly generated topological spaces is a closed symmetric monoidal category with tensor unit the 0-sphere.
Notice that by prop. also unpointed compactly generated spaces under Cartesian product form a closed symmetric monoidal category, hence a cartesian closed category
The fact that is still closed symmetric monoidal but no longer Cartesian exhibits as being “more linear” than . The “full linearization” of is the closed symmteric monoidal category of structured spectra under smash product of spectra which we discuss in section 1.
Due to the idempotency (cor. ) it is useful to know plenty of conditions under which a given topological space is already compactly generated, for then applying to it does not change it and one may continue working as in .
Example
Every CW-complex is compactly generated.
Proof
Since a CW-complex is a Hausdorff space, by prop. and prop. its -closed subsets are precisely those whose intersection with every compact subspace is closed.
Since a CW-complex is a colimit in Top over attachments of standard n-disks (its cells), by the characterization of colimits in (prop.) a subset of is open or closed precisely if its restriction to each cell is open or closed, respectively. Since the -disks are compact, this implies one direction: if a subset of intersected with all compact subsets is closed, then is closed.
For the converse direction, since a CW-complex is a Hausdorff space and since compact subspaces of Hausdorff spaces are closed, the intersection of a closed subset with a compact subset is closed.
For completeness we record further classes of examples:
Example
The category of compactly generated topological spaces includes
-
all first-countable topological spaces,
hence in particular
Recall that by corollary , all colimits of compactly generated spaces are again compactly generated.
Example
The product topological space of a CW-complex with a compact CW-complex, and more generally with a locally compact CW-complex, is compactly generated.
(Hatcher “Topology of cell complexes”, theorem A.6)
More generally:
Proposition
For a compactly generated space and a locally compact Hausdorff space, then the product topological space is compactly generated.
e.g. (Strickland 09, prop. 26)
Finally we check that the concept of homotopy and homotopy groups does not change under passing to compactly generated spaces:
Proposition
For every topological space , the canonical function (the adjunction unit) is a weak homotopy equivalence.
Proof
By example , example and lemma , continuous functions and their left homotopies are in bijection with functions and their homotopies .
Theorem
The restriction of the model category structure on from theorem along the inclusion of def. is still a model category structure, which is cofibrantly generated by the same sets (def. ) and (def. ) The coreflection of cor. is a Quillen equivalence (def. )
Proof
By example , the sets and are indeed in . By example all arguments above about left homotopies between maps out of these basic cells go through verbatim in . Hence the three technical lemmas above depending on actual point-set topology, topology, lemma , lemma and lemma , go through verbatim as before. Accordingly, since the remainder of the proof of theorem of follows by general abstract arguments from these, it also still goes through verbatim for (repeatedly use the small object argument and the retract argument to establish the two weak factorization systems).
Hence the (acyclic) cofibrations in are identified with those in , and so the inclusion is a part of a Quillen adjunction (def. ). To see that this is a Quillen equivalence (def. ), it is sufficient to check that for a compactly generated space then a continuous function is a weak homotopy equivalence (def. ) precisely if the adjunct is a weak homotopy equivalence. But, by lemma , is the same function as , just considered with different codomain. Hence the result follows with prop. .
Compactly generated weakly Hausdorff topological spaces
While the inclusion of def. does satisfy the requirement that it gives a cartesian closed category with all limits and colimits and containing all CW-complexes, one may ask for yet smaller subcategories that still share all these properties but potentially exhibit further convenient properties still.
A popular choice introduced in (McCord 69) is to add the further restriction to topopological spaces which are not only compactly generated but also weakly Hausdorff. This was motivated from (Steenrod 67) where compactly generated Hausdorff spaces were used by the observation ((McCord 69, section 2)) that Hausdorffness is not preserved my many colimit operations, notably not by forming quotient spaces.
On the other hand, in above we wouldn’t have imposed Hausdorffness in the first place. More intrinsic advantages of over are the following:
-
every pushout of a morphism in along a closed subspace inclusion in is again in
-
in quotient spaces are not only preserved by cartesian products (as is the case for all compactly generated spaces due to being a left adjoint, according to cor. ) but by all pullbacks
-
in the regular monomorphisms are the closed subspace inclusions
We will not need this here or in the following sections, but we briefly mention it for completenes:
Definition
A topological space is called weakly Hausdorff if for every continuous function
out of a compact Hausdorff space , its image is a closed subset of .
Proposition
Every Hausdorff space is a weakly Hausdorff space, def. .
Proof
Proposition
For a weakly Hausdorff topological space, def. , then a subset is -closed, def. , precisely if for every subset that is compact Hausdorff with respect to the subspace topology, then the intersection is a closed subset of .
e.g. (Strickland 09, lemma 1.4 (c))
Topological enrichment
So far the classical model structure on topological spaces which we established in theorem , as well as the projective model structures on topologically enriched functors induced from it in theorem , concern the hom-sets, but not the hom-spaces (def. ), i.e. the model structure so far has not been related to the topology on hom-spaces. The following statements say that in fact the model structure and the enrichment by topology on the hom-spaces are compatible in a suitable sense: we have an “enriched model category”. This implies in particular that the product/hom-adjunctions are Quillen adjunctions, which is crucial for a decent discusson of the derived functors of the suspension/looping adjunction below.
Definition
Let and be morphisms in , def. . Their pushout product
is the universal morphism in the following diagram
Example
If and are inclusions, then their pushout product from def. is the inclusion
For instance
is the inclusion of two adjacent edges of a square into the square.
Example
The pushout product with an initial morphism is just the ordinary Cartesian product functor
i.e.
Proof
The product topological space with the empty space is the empty space, hence the map is an isomorphism, and so the pushout in the pushout product is . From this one reads off the universal map in question to be :
Example
With
the generating cofibrations (def. ) and generating acyclic cofibrations (def. ) of (theorem ), then their pushout-products (def. ) are
Proof
To see this, it is profitable to model n-disks and n-spheres, up to homeomorphism, as -cubes and their boundaries . For the idea of the proof, consider the situation in low dimensions, where one readily sees pictorially that
and
Generally, may be represented as the space of -tuples of elements in , and as the suspace of tuples for which at least one of the coordinates is equal to 0 or to 1.
Accordingly, is the subspace of -tuples, such that at least one of the first coordinates is equal to 0 or 1, while is the subspace of -tuples such that east least one of the last coordinates is equal to 0 or to 1. Therefore
And of course it is clear that . This shows the first case.
For the second, use that is contractible to in , and that is a subspace of .
Definition
Let and be two morphisms in , def. . Their pullback powering is
being the universal morphism in
Proposition
Let be three morphisms in , def. . Then for their pushout-products (def. ) and pullback-powerings (def. ) the following lifting properties are equivalent (“Joyal-Tierney calculus”):
Proof
We claim that by the cartesian closure of , and carefully collecting terms, one finds a natural bijection between commuting squares and their lifts as follows:
where the tilde denotes product/hom-adjuncts, for instance
etc.
To see this in more detail, observe that both squares above each represent two squares from the two components into the fiber product and out of the pushout, respectively, as well as one more square exhibiting the compatibility condition on these components:
Proposition
The pushout-product in (def. ) of two classical cofibrations is a classical cofibration:
If one of them is acyclic, then so is the pushout-product:
Proof
Regarding the first point:
Hence
where all logical equivalences used are those of prop. and where all implications appearing are by the closure property of lifting problems, prop. .
Regarding the second point: By example we moreover have
and the conclusion follows by the same kind of reasoning.
Remark
In model category theory the property in proposition is referred to as saying that the model category from theorem
-
is a monoidal model category with respect to the Cartesian product on ;
-
is an enriched model category, over itself.
A key point of what this entails is the following:
Proposition
For cofibrant (a retract of a cell complex) then the product-hom-adjunction for (prop. ) is a Quillen adjunction
Proof
By example we have that the left adjoint functor is equivalently the pushout product functor with the initial morphism of :
By assumption is a cofibration, and hence prop. says that this is a left Quillen functor.
The statement and proof of prop. has a direct analogue in pointed topological spaces
Proposition
For cofibrant with respect to the classical model structure on pointed compactly generated topological spaces (theorem , prop. ) (hence a retract of a cell complex with non-degenerate basepoint, remark ) then the pointed product-hom-adjunction from corollary is a Quillen adjunction (def. ):
Proof
Let now denote the smash pushout product and the smash pullback powering defined as in def. and def. , but with Cartesian product replaced by smash product (def. ) and compactly generated mapping space replaced by pointed mapping spaces (def. ).
By theorem is cofibrantly generated by and . Example gives that for and then
and
Hence the pointed analog of prop. holds and therefore so does the pointed analog of the conclusion in prop. .
Model structure on topological functors
With classical topological homotopy theory in hand (theorem , theorem ), it is straightforward now to generalize this to a homotopy theory of topological diagrams. This is going to be the basis for the stable homotopy theory of spectra, because spectra may be identified with certain topological diagrams (prop.).
Technically, “topological diagram” here means “Top-enriched functor”. We now discuss what this means and then observe that as an immediate corollary of theorem we obtain a model category structure on topological diagrams.
As a by-product, we obtain the model category theory of homotopy colimits in topological spaces, which will be useful.
In the following we say Top-enriched category and Top-enriched functor etc. for what often is referred to as “topological category” and “topological functor” etc. As discussed there, these latter terms are ambiguous.
Literature (Riehl, chapter 3) for basics of enriched category theory; (Piacenza 91) for the projective model structure on topological functors.
Definition
A topologically enriched category is a -enriched category, hence:
-
for each a compactly generated topological space (def. )
called the space of morphisms or the hom-space between and ;
-
for each a continuous function
out of the cartesian product (by cor. : the image under of the product topological space), called the composition operation;
-
for each a point , called the identity morphism on
such that the composition is associative and unital.
Similarly a pointed topologically enriched category is such a structure with replaced by (def. ) and with the Cartesian product replaced by the smash product (def. ) of pointed topological spaces.
Remark
Given a (pointed) topologically enriched category as in def. , then forgetting the topology on the hom-spaces (along the forgetful functor ) yields an ordinary locally small category with
It is in this sense that is a category with extra structure, and hence “enriched”.
The archetypical example is itself:
Example
The category (def. ) canonically obtains the structure of a topologically enriched category, def. , with hom-spaces given by the compactly generated mapping spaces (def. )
and with composition
given by the adjunct under the (product mapping-space)-adjunction from prop. of the evaluation morphisms
Similarly, pointed compactly generated topological spaces form a pointed topologically enriched category, using the pointed mapping spaces from example :
Definition
A topologically enriched functor between two topologically enriched categories
is a -enriched functor, hence:
-
a function
of objects;
-
for each a continuous function
of hom-spaces,
such that this preserves composition and identity morphisms in the evident sense.
A homomorphism of topologically enriched functors
is a -enriched natural transformation: for each a choice of morphism such that for each pair of objects the two continuous functions
and
agree.
We write for the resulting category of topologically enriched functors.
Remark
The condition on an enriched natural transformation in def. is just that on an ordinary natural transformation on the underlying unenriched functors, saying that for every morphisms there is a commuting square
Example
For any topologically enriched category, def. then a topologically enriched functor (def. )
to the archetypical topologically enriched category from example may be thought of as a topologically enriched copresheaf, at least if is small (in that its class of objects is a proper set).
Hence the category of topologically enriched functors
according to def. may be thought of as the (co-)presheaf category over in the realm of topological enriched categories.
A functor is equivalently
-
a compactly generated topological space for each object ;
-
for all pairs of objects
such that composition is respected, in the evident sense.
For every object , there is a topologically enriched representable functor, denoted or which sends objects to
and whose action on morphisms is, under the above identification, just the composition operation in .
Proposition
For any small topologically enriched category, def. then the enriched functor category from example has all limits and colimits, and they are computed objectwise:
if
is a diagram of functors and is any object, then
and
Proof
First consider the underlying diagram of functors where the topology on the hom-spaces of and of has been forgotten. Then one finds
and
by the universal property of limits and colimits. (Given a morphism of diagrams then a unique compatible morphism between their limits or colimits, respectively, is induced as the universal factorization of the morphism of diagrams regarded as a cone or cocone, respectvely, over the codomain or domain diagram, respectively).
Hence it only remains to see that equipped with topology, these limits and colimits in become limits and colimits in . That is just the statement of prop. with corollary .
Definition
Let be a topologically enriched category, def. , with its category of topologically enriched copresheaves from example .
-
Define a functor
by forming objectwise cartesian products (hence of product topological spaces)
This is called the tensoring of over (Def. ).
-
Define a functor
by forming objectwise compactly generated mapping spaces (def. )
This is called the powering of over .
Analogously, for a pointed topologically enriched category, def. , with its category of pointed topologically enriched copresheaves from example , then:
-
Define a functor
by forming objectwise smash products (def. )
This is called the smash tensoring of over (Def. ).
-
Define a functor
by forming objectwise pointed mapping spaces (example )
This is called the pointed powering of over .
There is a full blown -enriched Yoneda lemma. The following records a slightly simplified version which is all that is needed here:
Proposition
(topologically enriched Yoneda-lemma)
Let be a topologically enriched category, def. , write for its category of topologically enriched (co-)presheaves, and for write for the topologically enriched functor that it represents, all according to example . Recall the tensoring operation from def. .
For , and , there is a natural bijection between
-
morphisms in ;
-
morphisms in .
In short:
Proof
Given a morphism consider its component
and restrict that to the identity morphism in the first argument
We claim that just this already uniquely determines all components
of , for all : By definition of the transformation (def. ), the two functions
and
agree. This means (remark ) that they may be thought of jointly as a function with values in commuting squares in of this form:
For any , consider the restriction of
to , hence restricting the above commuting squares to
This shows that is fixed to be the function
and this is a continuous function since all the operations it is built from are continuous.
Conversely, given a continuous function , define for each the function
Running the above analysis backwards shows that this determines a transformation .
Definition
For a small topologically enriched category, def. , write
and
for the sets of morphisms given by tensoring (def. ) the representable functors (example ) with the generating cofibrations (def.) and acyclic generating cofibrations (def. ), respectively, of (theorem ).
These are going to be called the generating cofibrations and acyclic generating cofibrations for the projective model structure on topologically enriched functors over .
Analgously, for a pointed topologically enriched category, write
and
for the analogous construction applied to the pointed generating (acyclic) cofibrations of def. .
Definition
Given a small (pointed) topologically enriched category , def. , say that a morphism in the category of (pointed) topologically enriched copresheaves (), example , hence a natural transformation between topologically enriched functors, is
-
a projective weak equivalence, if for all the component is a weak homotopy equivalence (def. );
-
a projective fibration if for all the component is a Serre fibration (def. );
-
a projective cofibration if it is a retract (rmk. ) of an -relative cell complex (def. , def. ).
Write
and
for the categories of topologically enriched functors equipped with these classes of morphisms.
Theorem
The classes of morphisms in def. constitute a model category structure on and , called the projective model structure on enriched functors
and
These are cofibrantly generated model category, def. , with set of generating (acyclic) cofibrations the sets , and , from def. , respectively.
Proof
By prop. the category has all limits and colimits, hence it remains to check the model structure
But via the enriched Yoneda lemma (prop. ) it follows that proving the model structure reduces objectwise to the proof of theorem , theorem . In particular, the technical lemmas , and generalize immediately to the present situation, with the evident small change of wording:
For instance, the fact that a morphism of topologically enriched functors that has the right lifting property against the elements of is a projective weak equivalence, follows by noticing that for fixed the enriched Yoneda lemma prop. gives a natural bijection of commuting diagrams (and their fillers) of the form
and hence the statement follows with part A) of the proof of lemma .
With these three lemmas in hand, the remaining formal part of the proof goes through verbatim as above: repeatedly use the small object argument (prop. ) and the retract argument (prop. ) to establish the two weak factorization systems. (While again the structure of a category with weak equivalences is evident.)
Example
Given examples and , the next evident example of a pointed topologically enriched category besides itself is the functor category
The only technical problem with this is that is not a small category (it has a proper class of objects), which means that the existence of all limits and colimits via prop. may (and does) fail.
But so we just restrict to a small topologically enriched subcategory. A good choice is the full subcategory
of topological spaces homoemorphic to finite CW-complexes. The resulting projective model category (via theorem )
is also also known as the strict model structure for excisive functors. (This terminology is the special case for of the terminology “n-excisive functors” as used in “Goodwillie calculus”, a homotopy-theoretic analog of differential calculus.) After enlarging its class of weak equivalences while keeping the cofibrations fixed, this will become Quillen equivalent to a model structure for spectra. This we discuss in part 1.2, in the section on pre-excisive functors.
One consequence of theorem is the model category theoretic incarnation of the theory of homotopy colimits.
Observe that ordinary limits and colimits (def. ) are equivalently characterized in terms of adjoint functors:
Let be any category and let be a small category. Write for the corresponding functor category. We may think of its objects as -shaped diagrams in , and of its morphisms as homomorphisms of these diagrams. There is a canonical functor
which sends each object of to the diagram that is constant on this object. Inspection of the definition of the universal properties of limits and colimits on one hand, and of left adjoint and right adjoint functors on the other hand, shows that
-
precisely when has all colimits of shape , then the functor has a left adjoint functor, which is the operation of forming these colimits:
-
precisely when has all limits of shape , then the functor has a right adjoint functor, which is the operation of forming these limits.
Proposition
Let be a small topologically enriched category (def. ). Then the -adjunction
is a Quillen adjunction (def. ) between the projective model structure on topological functors on , from theorem , and the classical model structure on topological spaces from theorem .
Similarly, if is enriched in pointed topological spaces, then for the classical model structure on pointed topological spaces (prop. , theorem ) the adjunction
is a Quillen adjunction.
Proof
Since the fibrations and weak equivalences in the projective model structure (def. ) on the functor category are objectwise those of and of , respectively, it is immediate that the functor preserves these. In particular it preserves fibrations and acyclic fibrations and so the claim follows (prop. ).
Definition
In the situation of prop. we say that the left derived functor (def. ) of the colimit functor is the homotopy colimit
and
Remark
Since every object in and in is fibrant, the homotopy colimit of any diagram , according to def. , is (up to weak homotopy equivalence) the result of forming the ordinary colimit of any projectively cofibrant replacement .
Example
Write for the poset (def. ) of natural numbers, hence for the small category (with at most one morphism from any given object to any other given object) that looks like
Regard this as a topologically enriched category with the, necessarily, discrete topology on its hom-sets.
Then a topologically enriched functor
is just a plain functor and is equivalently a sequence of continuous functions (morphisms in ) of the form (also called a cotower)
It is immediate to check that those sequences which are cofibrant in the projective model structure (theorem ) are precisely those for which
-
all component morphisms are cofibrations in or , respectively, hence retracts (remark ) of relative cell complex inclusions (def. );
-
the object , and hence all other objects, are cofibrant, hence are retracts of cell complexes (def. ).
By example it is immediate that the operation of forming colimits sends projective (acyclic) cofibrations between sequences of topological spaces to (acyclic) cofibrations in the classical model structure on pointed topological spaces. On those projectively cofibrant sequences where every map is not just a retract of a relative cell complex inclusion, but a plain relative cell complex inclusion, more is true:
Proposition
In the projective model structures on cotowers in topological spaces, and from def. , the following holds:
-
The colimit functor preserves fibrations between sequences of relative cell complex inclusions;
-
Let be a finite category, let be a finite diagram of sequences of relative cell complexes. Then there is a weak homotopy equivalence
from the colimit over the limit sequnce to the limit of the colimits of sequences.
Proof
Regarding the first statement:
Use that both and are cofibrantly generated model categories (theorem ) whose generating acyclic cofibrations have compact topological spaces as domains and codomains. The colimit over a sequence of relative cell complexes (being a transfinite composition) yields another relative cell complex, and hence lemma says that every morphism out of the domain or codomain of a generating acyclic cofibration into this colimit factors through a finite stage inclusion. Since a projective fibration is a degreewise fibration, we have the lifting property at that finite stage, and hence also the lifting property against the morphisms of colimits.
Regarding the second statement:
This is a model category theoretic version of a standard fact of plain category theory, which says that in the category Set of sets, filtered colimits commute with finite limits in that there is an isomorphism of sets of the form which we have to prove is a weak homotopy equivalence of topological spaces. But now using that weak homotopy equivalences are detected by forming homotopy groups (def. ), hence hom-sets out of n-spheres, and since -spheres are compact topological spaces, lemma says that homming out of -spheres commutes over the colimits in question. Moreover, generally homming out of anything commutes over limits, in particular finite limits (every hom functor is left exact functor in the second variable). Therefore we find isomorphisms of the form
and similarly for the left homotopies (and similarly for the pointed case). This implies the claimed isomorphism on homotopy groups.
-Groupoids II): Simplicial homotopy theory
With groupoids and chain complexes we have seen two kinds of objects which support concepts of homotopy theory, such as a concept of homotopy equivalence between them (equivalence of groupoids on the one hand, and quasi-isomorphism on the other). In some sense these two cases are opposite extremes in the more general context of homotopy theory:
-
chain complexes have homotopical structure (e.g. chain homology) in arbitrary high degree, i.e. they may be homotopy n-types for arbitrary , but they are fully abelian in that there is never any nonabelian group structure in a chain complex, not is there any non-trivial action of the homology groups of a chain complex on each other;
-
groupoids have more general non-abelian structure, for every (nonabelian) group there is a groupoid which has this as its fundamental group, but this fundamental group (in degree 1) is already the highest homotopical structure they carry, groupoids are necessarily homotopy 1-types.
On the other hand, both groupoids and chain complexes naturally have incarnations in the joint context of simplicial sets. We now discuss how their common joint generalization is given by those simplicial sets whose simplices have a sensible notion of composition and inverses, the Kan complexes.
Kan complexes serve as a standard powerful model on which the complete formulation of homotopy theory (without geometry) may be formulated.
Simplicial sets
The concept of simplicial sets is secretly well familiar already in basic algebraic topology: it reflects just the abstract structure carried by the singular simplicial complexes of topological spaces, as in the definition of singular homology and singular cohomology.
Conversely, every simplicial set may be geometrically realized as a topological space. These two adjoint operations turn out to exhibit the homotopy theory of simplicial sets as being equivalent (Quillen equivalent) to the homotopy theory of topological spaces. For some purposes, working in simplicial homotopy theory is preferable over working with topological homotopy theory.
Definition
For , the topological n-simplex is, up to homeomorphism, the topological space whose underlying set is the subset
of the Cartesian space , and whose topology is the subspace topology induces from the canonical topology in .
Example
For this is the point, .
For this is the standard interval object .
For this is the filled triangle.
For this is the filled tetrahedron.
Definition
For , and , the th -face (inclusion) of the topological -simplex, def. , is the subspace inclusion
induced under the coordinate presentation of def. , by the inclusion
which “omits” the th canonical coordinate:
Example
The inclusion
is the inclusion
of the “right” end of the standard interval. The other inclusion
is that of the “left” end .
(graphics taken from Friedman 08)
Definition
For and the th degenerate -simplex (projection) is the surjective map
induced under the barycentric coordinates of def. under the surjection
which sends
Definition
For Top and , a singular -simplex in is a continuous map
from the topological -simplex, def. , to .
Write
for the set of singular -simplices of .
(graphics taken from Friedman 08)
The sets here are closely related by an interlocking system of maps that make them form what is called a simplicial set, and as such the collection of these sets of singular simplices is called the singular simplicial complex of . We discuss the definition of simplicial sets now and then come back to this below in def. .
Since the topological -simplices from def. sit inside each other by the face inclusions of def.
and project onto each other by the degeneracy maps, def.
we dually have functions
that send each singular -simplex to its -face and functions
that regard an -simplex as beign a degenerate (“thin”) -simplex. All these sets of simplices and face and degeneracy maps between them form the following structure.
Definition
A simplicial set is
-
for each injective map of totally ordered sets
a function – the th face map on -simplices;
-
for each surjective map of totally ordered sets
a function – the th degeneracy map on -simplices;
such that these functions satisfy the following identities, called the_simplicial identities:
-
if ,
-
if .
For two simplicial sets, a morphism of simplicial sets is for each a function between sets of -simplices, such that these functions are compatible with all the face and degeneracy maps.
This defines a category (Def. ) sSet of simplicial sets.
It is straightforward to check by explicit inspection that the evident injection and restriction maps between the sets of singular simplices make into a simplicial set. However for working with this, it is good to streamline a little:
Definition
The simplex category is the full subcategory of Cat on the free categories of the form
Remark
This is called the “simplex category” because we are to think of the object as being the “spine” of the -simplex. For instance for we think of as the “spine” of the triangle. This becomes clear if we don’t just draw the morphisms that generate the category , but draw also all their composites. For instance for we have_
Proposition
(simplicial sets are presheaves on the simplex category)
A functor
from the opposite category (Example ) of the simplex category (Def. ) to the category of sets, hence a presheaf on (Example ), is canonically identified with a simplicial set, def. .
Via this identification, the category sSet of simplicial sets (Def. ) is equivalent to the category of presheaves on the simplex category
In particular this means that sSet is a cosmos for enriched category theory (Example ), by Prop. .
Proof
One checks by inspection that the simplicial identities characterize precisely the behaviour of the morphisms in and .
This makes the following evident:
Example
The topological simplices from def. arrange into a cosimplicial object in Top, namely a functor
With this now the structure of a simplicial set on , def. , is manifest: it is just the nerve of with respect to , namely:
Definition
For a topological space its simplicial set of singular simplicies (often called the singular simplicial complex)
is given by composition of the functor from example with the hom functor of Top:
Remark
It turns out – this is the content of the homotopy hypothesis-theorem (Quillen 67) – that homotopy type of the topological space is entirely captured by its singular simplicial complex . Moreover, the geometric realization of is a model for the same homotopy type as that of , but with the special property that it is canonically a cell complex – a CW-complex. Better yet, is itself already good cell complex, namely a Kan complex. We come to this below.
Simplicial homotopy
The concept of homotopy of morphisms between simplicial sets proceeds in direct analogy with that in topological spaces.
Definition
For a simplicial set, def. , its simplicial cylinder object is the Cartesian product (formed in the category sSet, Prop. ).
between two morphisms
of simplicial sets is a morphism
such that the following diagram commutes
For a Kan complex, def. , its simplicial path space object is the function complex (formed in the category sSet, Prop. ).
between two morphisms
of simplicial sets is a morphism
such that the following diagram commutes
Proposition
For a Kan complex, def. , and any simplicial set, then left homotopy, def. , regarded as a relation
on the hom set , is an equivalence relation.
Definition
(homotopy equivalence in simplicial sets)
A morphism of simplicial sets is a left/right homotopy equivalence if there exists a morphisms and left/right homotopies (def. )
The the basic invariants of simplicial sets/Kan complexes in simplicial homotopy theory are their simplicial homotopy groups, to which we turn now.
Given that a Kan complex is a special simplicial set that behaves like a combinatorial model for a topological space, the simplicial homotopy groups of a Kan complex are accordingly the combinatorial analog of the homotopy groups of topological spaces: instead of being maps from topological spheres modulo maps from topological disks, they are maps from the boundary of a simplex modulo those from the simplex itself.
Accordingly, the definition of the discussion of simplicial homotopy groups is essentially literally the same as that of homotopy groups of topological spaces. One technical difference is for instance that the definition of the group structure is slightly more non-immediate for simplicial homotopy groups than for topological homotopy groups (see below).
Definition
For a Kan complex, then its 0th simplicial homotopy group (or set of connected components) is the set of equivalence classes of vertices modulo the equivalence relation
For a vertex and for , , then the underlying set of the th simplicial homotopy group of at – denoted – is, the set of equivalence classes of morphisms
from the simplicial -simplex to , such that these take the boundary of the simplex to , i.e. such that they fit into a commuting diagram in sSet of the form
where two such maps are taken to be equivalent is they are related by a simplicial homotopy
that fixes the boundary in that it fits into a commuting diagram in sSet of the form
These sets are taken to be equipped with the following group structure.
Definition
For a Kan complex, for , for and for two representatives of as in def. , consider the following -simplices in :
This corresponds to a morphism from a horn of the -simplex into . By the Kan complex property of this morphism has an extension through the -simplex
From the simplicial identities one finds that the boundary of the -simplex arising as the th boundary piece of is constant on
So represents an element in and we define a product operation on by
(e.g. Goerss-Jardine 99, p. 26)
Remark
All the degenerate -simplices in def. are just there so that the gluing of the two -cells and to each other can be regarded as forming the boundary of an -simplex except for one face. By the Kan extension property that missing face exists, namely . This is a choice of gluing composite of with .
Lemma
The product on homotopy group elements in def. is well defined, in that it is independent of the choice of representatives , and of the extension .
e.g. (Goerss-Jardine 99, lemma 7.1)
e.g. (Goerss-Jardine 99, theorem 7.2)
Remark
The first homotopy group, , is also called the fundamental group of .
Definition
(weak homotopy equivalence of simplicial sets)
For two Kan complexes, then a morphism
is called a weak homotopy equivalence if it induces isomorphisms on all simplicial homotopy groups, i.e. if
-
is a bijection of sets;
-
is an isomorphism of groups for all and all ; .
Kan complexes
Recall the definition of simplicial sets from above. Let
be the standard simplicial -simplex in SimpSet.
Definition
For each , , the -horn or -box is the subsimplicial set
which is the union of all faces except the one.
This is called an outer horn if or . Otherwise it is an inner horn.
Remark
Since sSet is a presheaf topos, unions of subobjects make sense and they are calculated objectwise, thus in this case dimensionwise. This way it becomes clear what the structure of a horn as a functor must therefore be: it takes to the collection of ordinal maps which do not have the element in the image.
Example
The inner horn, def. of the 2-simplex
with boundary
looks like
The two outer horns look like
and
respectively.
(graphics taken from Friedman 08)
Definition
A Kan complex is a simplicial set that satisfies the Kan condition,
-
which says that all horns of the simplicial set have fillers/extend to simplices;
-
which means equivalently that the unique homomorphism from to the point (the terminal simplicial set) is a Kan fibration;
-
which means equivalently that for all diagrams in sSet of the form
there exists a diagonal morphism
completing this to a commuting diagram;
-
which in turn means equivalently that the map from -simplices to -horns is an epimorphism
Proposition
For a topological space, its singular simplicial complex , def. , is a Kan complex, def. .
Proof
The inclusions of topological horns into topological simplices are retracts, in that there are continuous maps given by “squashing” a topological -simplex onto parts of its boundary, such that
Therefore the map is an epimorphism, since it is equal to to which has a right inverse .
More generally:
Definition
A morphism in sSet is called a Kan fibration if it has the right lifting property again all horn inclusions, def. , hence if for every commuting diagram of the form
there exists a lift
This is the simplicial incarnation of the concept of Serre fibrations of topological spaces:
Definition
A continuous function between topological spaces is a Serre fibration if for all CW-complexes and for every commuting diagram in Top of the form
there exists a lift
Proposition
A continuous function is a Serre fibration, def. , precisely if (def. ) is a Kan fibration, def. .
The proof uses the basic tool of nerve and realization-adjunction to which we get to below in prop. .
Proof
First observe that the left lifting property against all for a CW-complex is equivalent to left lifting against geometric realization of horn inclusions. Then apply the natural isomorphism , given by the adjunction of prop. and example , to the lifting diagrams.
Lemma
Let be a Kan fibration, def. , and let be two morphisms. If there is a left homotopy (def. ) between these maps, then there is a fiberwise homotopy equivalence, def. , between the pullback fibrations .
(e.g. Goerss-Jardine 99, chapter I, lemma 10.6)
While simplicial sets have the advantage of being purely combinatorial structures, the singular simplicial complex of any given topological space, def. is in general a huge simplicial set which does not lend itself to detailed inspection. The following is about small models.
Definition
A Kan fibration , def. , is called a minimal Kan fibration if for any two cells in the same fiber with the same boundary if they are homotopic relative their boundary, then they are already equal.
More formally, is minimal precisely if for every commuting diagram of the form
then the two composites
are equal.
Proposition
The pullback (in sSet) of a minimal Kan fibration, def. , along any morphism is again a mimimal Kan fibration.
(Goerss-Jardine 99, chapter I, section 4, Joyal-Tierney 05, section 31)
Proposition
For every Kan fibration, def. , there exists a fiberwise strong deformation retract to a minimal Kan fibration, def. .
(e.g. Goerss-Jardine 99, chapter I, prop. 10.3, Joyal-Tierney 05, theorem 3.3.1, theorem 3.3.3).
Proof idea
Choose representatives by induction, use that in the induction step one needs lifts of anodyne extensions against a Kan fibration, which exist.
Lemma
A morphism between minimal Kan fibrations, def. , which is fiberwise a homotopy equivalence, def. , is already an isomorphism.
(e.g. Goerss-Jardine 99, chapter I, lemma 10.4)
Proof idea
Show the statement degreewise. In the induction one needs to lift anodyne extensions agains a Kan fibration.
Lemma
Every minimal Kan fibration, def. , over a connected base is a simplicial fiber bundle, locally trivial over every simplex of the base.
(e.g. Goerss-Jardine 99, chapter I, corollary 10.8)
Proof
By assumption of the base being connected, the classifying maps for the fibers over any two vertices are connected by a zig-zag of homotopies, hence by lemma the fibers are connected by homotopy equivalences and then by prop. and lemma they are already isomorphic. Write for this typical fiber.
Moreover, for all the morphisms are left homotopic to and so applying lemma and prop. once more yields that the fiber over each is isomorphic to .
Groupoids as Kan complexes
Definition
-
a pair of sets (the set of objects) and (the set of morphisms)
-
equipped with functions
where the fiber product on the left is that over ,
such that
-
takes values in endomorphisms;
-
defines a partial composition operation which is associative and unital for the identities; in particular
and ;
-
every morphism has an inverse under this composition.
Remark
This data is visualized as follows. The set of morphisms is
and the set of pairs of composable morphisms is
The functions are those which send, respectively, these triangular diagrams to the left morphism, or the right morphism, or the bottom morphism.
Example
For a set, it becomes a groupoid by taking to be the set of objects and adding only precisely the identity morphism from each object to itself
Example
For a group, its delooping groupoid has
-
;
-
.
For and two groups, group homomorphisms are in natural bijection with groupoid homomorphisms
In particular a group character is equivalently a groupoid homomorphism
Here, for the time being, all groups are discrete groups. Since the circle group also has a standard structure of a Lie group, and since later for the discussion of Chern-Simons type theories this will be relevant, we will write from now on
to mean explicitly the discrete group underlying the circle group. (Here “” denotes the “flat modality”.)
Example
For a set, a discrete group and an action of on (a permutation representation), the action groupoid or homotopy quotient of by is the groupoid
with composition induced by the product in . Hence this is the groupoid whose objects are the elements of , and where morphisms are of the form
for , .
As an important special case we have:
Example
For a discrete group and the trivial action of on the point (the singleton set), the corresponding action groupoid according to def. is the delooping groupoid of according to def. :
Another canonical action is the action of on itself by right multiplication. The corresponding action groupoid we write
The constant map induces a canonical morphism
This is known as the -universal principal bundle. See below in for more on this.
Example
For a topological space, its fundamental groupoid is
- points in ;
- continuous paths in modulo homotopy that leaves the endpoints fixed.
Example
For any groupoid, there is the path space groupoid with
-
;
-
commuting squares in =
This comes with two canonical homomorphisms
which are given by endpoint evaluation, hence which send such a commuting square to either its top or its bottom hirizontal component.
Definition
For two morphisms between groupoids, a homotopy (a natural transformation) is a homomorphism of the form (with codomain the path space object of as in example ) such that it fits into the diagram as depicted here on the right:
Definition (Notation)
Here and in the following, the convention is that we write
-
(with the subscript decoration) when we regard groupoids with just homomorphisms (functors) between them,
-
(without the subscript decoration) when we regard groupoids with homomorphisms (functors) between them and homotopies (natural transformations) between these
The unbulleted version of groupoids are also called homotopy 1-types (or often just their homotopy-equivalence classes are called this way.) Below we generalize this to arbitrary homotopy types (def. ).
Definition
A (homotopy-) equivalence of groupoids is a morphism which has a left and right inverse up to homotopy.
Example
The map
which picks any point and sends to the loop based at that point which winds around times, is an equivalence of groupoids.
Proposition
Assuming the axiom of choice in the ambient set theory, every groupoid is equivalent to a disjoint union of delooping groupoids, example – a skeleton.
Remark
The statement of prop. becomes false as when we pass to groupoids that are equipped with geometric structure. This is the reason why for discrete geometry all Chern-Simons-type field theories (namely Dijkgraaf-Witten theory-type theories) fundamentally involve just groups (and higher groups), while for nontrivial geometry there are genuine groupoid theories, for instance the AKSZ sigma-models. But even so, Dijkgraaf-Witten theory is usefully discussed in terms of groupoid technology, in particular since the choice of equivalence in prop. is not canonical.
Definition
Given two morphisms of groupoids their homotopy fiber product
hence the ordinary iterated fiber product over the path space groupoid, as indicated.
Remark
An ordinary fiber product of groupoids is given simply by the fiber product of the underlying sets of objects and morphisms:
Example
For a groupoid, a group and a map into its delooping, the pullback of the -universal principal bundle of example is equivalently the homotopy fiber product of with the point over :
Namely both squares in the following diagram are pullback squares
(This is the first example of the more general phenomenon of universal principal infinity-bundles.)
Example
For a groupoid and a point in it, we call
the loop space groupoid of .
For a group and its delooping groupoid from example , we have
Hence is the loop space object of its own delooping, as it should be.
Proof
We are to compute the ordinary limiting cone in
In the middle we have the groupoid whose objects are elements of and whose morphisms starting at some element are labeled by pairs of elements and end at . Using remark the limiting cone is seen to precisely pick those morphisms in such that these two elements are constant on the neutral element , hence it produces just the elements of regarded as a groupoid with only identity morphisms, as in example .
Proposition
The free loop space object is
Proof
Notice that . Therefore the path space object has
-
objects are pairs of morphisms in ;
-
morphisms are commuting squares of such.
Now the fiber product in def. picks in there those pairs of morphisms for which both start at the same object, and both end at the same object. Therefore is the groupoid whose
-
objects are diagrams in of the form
-
morphism are cylinder-diagrams over these.
One finds along the lines of example that this is equivalent to maps from into and homotopies between these.
Remark
Even though all these models of the circle are equivalent, below the special appearance of the circle in the proof of prop. as the combination of two semi-circles will be important for the following proofs. As we see in a moment, this is the natural way in which the circle appears as the composition of an evaluation map with a coevaluation map.
Example
For a discrete group, the free loop space object of its delooping is , the action groupoid, def. , of the adjoint action of on itself:
Example
For an abelian group such as we have
Example
Let be a group homomorphism, hence a group character. By example this has a delooping to a groupoid homomorphism
Under the free loop space object construction this becomes
hence
So by postcomposing with the projection on the first factor we recover from the general homotopy theory of groupoids the statement that a group character is a class function on conjugacy classes:
Definition
For a groupoid, def. , its simplicial nerve is the simplicial set with
the set of sequences of composable morphisms of length , for ;
with face maps
being,
-
for the functions that remembers the th object;
-
for
-
the two outer face maps and are given by forgetting the first and the last morphism in such a sequence, respectively;
-
the inner face maps are given by composing the th morphism with the st in the sequence.
-
The degeneracy maps
are given by inserting an identity morphism on .
Remark
Spelling this out in more detail: write
for the set of sequences of composable morphisms. Given any element of this set and , write
for the comosition of the two morphism that share the th vertex.
With this, face map acts simply by “removing the index ”:
Similarly, writing
for the identity morphism on the object , then the degenarcy map acts by “repeating the th index”
This makes it manifest that these functions organise into a simplicial set.
Proposition
These collections of maps in def. satisfy the simplicial identities, hence make the nerve into a simplicial set. Moreover, this simplicial set is a Kan complex, where each horn has a unique filler (extension to a simplex).
(A 2-coskeletal Kan complex.)
Proposition
The nerve operation constitutes a full and faithful functor
Chain complexes as Kan complexes
In the familiar construction of singular homology recalled above one constructs the alternating face map chain complex of the simplicial abelian group of singular simplices, def. . This construction is natural and straightforward, but the result chain complex tends to be very “large” even if its chain homology groups end up being very “small”. But in the context of homotopy theory one is to consider all objects notup to isomorphism, but of to weak equivalence, which for chain complexes means up to quasi-isomorphisms. Hence one should look for the natural construction of “smaller” chain complexes that are still quasi-isomorphic to these alternating face map complexes. This is accomplished by the normalized chain complex construction:
Definition
For a simplicial abelian group its alternating face map complex of is the chain complex which
-
in degree is given by the group itself
-
with differential given by the alternating sum of face maps (using the abelian group structure on )
Proof
Using the simplicial identity, prop. , for one finds:
Definition
Given a simplicial abelian group , its normalized chain complex or Moore complex is the -graded chain complex which
-
is in degree the joint kernel
of all face maps except the 0-face;
-
with differential given by the remaining 0-face map
Remark
We may think of the elements of the complex , def. , in degree as being -dimensional disks in all whose boundary is captured by a single face:
-
an element in degree 1 is a 1-disk
-
an element is a 2-disk
-
a degree 2 element in the kernel of the boundary map is such a 2-disk that is closed to a 2-sphere
etc.
Definition
Given a simplicial group (or in fact any simplicial set), then an element is called degenerate (or thin) if it is in the image of one of the simplicial degeneracy maps . All elements of are regarded a non-degenerate. Write
for the subgroup of which is generated by the degenerate elements (i.e. the smallest subgroup containing all the degenerate elements).
Definition
For a simplicial abelian group its alternating face maps chain complex modulo degeneracies, is the chain complex
-
which in degree 0 equals is just ;
-
which in degree is the quotient group obtained by dividing out the group of degenerate elements, def. :
-
whose differential is the induced action of the alternating sum of faces on the quotient (which is well-defined by lemma ).
Lemma
Def. is indeed well defined in that the alternating face map differential respects the degenerate subcomplex.
Proof
Using the mixed simplicial identities we find that for a degenerate element, its boundary is
which is again a combination of elements in the image of the degeneracy maps.
Proposition
Given a simplicial abelian group , the evident composite of natural morphisms
from the normalized chain complex, def. , into the alternating face map complex modulo degeneracies, def. , (inclusion followed by projection to the quotient) is a natural isomorphism of chain complexes.
e.g. (Goerss-Jardine, theorem III 2.1).
Corollary
For a simplicial abelian group, there is a splitting
of the alternating face map complex, def. as a direct sum, where the first direct summand is naturally isomorphic to the normalized chain complex of def. and the second is the degenerate cells from def. .
Proof
By prop. there is an inverse to the diagonal composite in
This hence exhibits a splitting of the short exact sequence given by the quotient by .
Theorem (Eilenberg-MacLane)
Given a simplicial abelian group , then the inclusion
of the normalized chain complex, def. into the full alternating face map complex, def. , is a natural quasi-isomorphism and in fact a natural chain homotopy equivalence, i.e. the complex is null-homotopic.
(Goerss-Jardine, theorem III 2.4)
Corollary
Given a simplicial abelian group , then the projection chain map
from its alternating face maps complex, def. , to the alternating face map complex modulo degeneracies, def. , is a quasi-isomorphism.
Proof
Consider the pre-composition of the map with the inclusion of the normalized chain complex, def. .
By theorem the vertical map is a quasi-isomorphism and by prop. the composite diagonal map is an isomorphism, hence in particular also a quasi-isomorphism. Since quasi-isomorphisms satisfy the two-out-of-three property, it follows that also the map in question is a quasi-isomorphism.
Example
Consider the 1-simplex regarded as a simplicial set, and write for the simplicial abelian group which in each degree is the free abelian group on the simplices in .
This simplicial abelian group starts out as
(where we are indicating only the face maps for notational simplicity).
Here the first , the direct sum of two copies of the integers, is the group of 0-chains generated from the two endpoints and of , i.e. the abelian group of formal linear combinations of the form
The second is the abelian group generated from the three (!) 1-simplicies in , namely the non-degenerate edge and the two degenerate cells and , hence the abelian group of formal linear combinations of the form
The two face maps act on the basis 1-cells as
Now of course most of the (infinitely!) many simplices inside are degenerate. In fact the only non-degenerate simplices are the two 0-cells and and the 1-cell . Hence the alternating face maps complex modulo degeneracies, def. , of is simply this:
Notice that alternatively we could consider the topological 1-simplex and its singular simplicial complex in place of the smaller , then the free simplicial abelian group of that. The corresponding alternating face map chain complex is “huge” in that in each positive degree it has a free abelian group on uncountably many generators. Quotienting out the degenerate cells still leaves uncountably many generators in each positive degree (while every singular -simplex in is “thin”, only those whose parameterization is as induced by a degeneracy map are actually regarded as degenerate cells here). Hence even after normalization the singular simplicial chain complex is “huge”. Nevertheless it is quasi-isomorphic to the tiny chain complex found above.
The statement of the Dold-Kan correspondence now is the following.
Theorem
For an abelian category there is an equivalence of categories
between
-
the category of simplicial objects in ;
where
- is the normalized chains complex/normalized Moore complex functor.
(Dold 58, Kan 58, Dold-Puppe 61).
Theorem (Kan)
For the case that is the category Ab of abelian groups, the functors and are nerve and realization with respect to the cosimplicial chain complex
that sends the standard -simplex to the normalized Moore complex of the free simplicial abelian group on the simplicial set , i.e.
This is due to (Kan 58).
More explicitly we have the following
Proposition
-
For the simplicial abelian group is in degree given by
and for a morphism in the corresponding map
is given on the summand indexed by some by the composite
where
is the epi-mono factorization of the composite .
-
The natural isomorphism is given on by the map
which on the direct summand indexed by is the composite
-
The natural isomorphism is on a chain complex given by the composite of the projection
with the inverse
of
(which is indeed an isomorphism, as discussed at Moore complex).
This is spelled out in (Goerss-Jardine, prop. 2.2 in section III.2).
Proposition
With the explicit choice for as above we have that and form an adjoint equivalence
This is for instance (Weibel, exercise 8.4.2).
Remark
It follows that with the inverse structure maps, we also have an adjunction the other way round: .
Hence in conclusion the Dold-Kan correspondence allows us to regard chain complexes (in non-negative degree) as, in particular, special simplicial sets. In fact as simplicial sets they are Kan complexes and hence infinity-groupoids:
Theorem (J. C. Moore)
The simplicial set underlying any simplicial group (by forgetting the group structure) is a Kan complex.
This is due to (Moore, 1954)
In fact, not only are the horn fillers guaranteed to exist, but there is an algorithm that provides explicit fillers. This implies that constructions on a simplicial group that use fillers of horns can often be adjusted to be functorial by using the algorithmically defined fillers. An argument that just uses ‘existence’ of fillers can be refined to give something more ‘coherent’.
Proof
Let be a simplicial group.
Here is the explicit algorithm that computes the horn fillers:
Let give a horn in , so the s are simplices that fit together as if they were all but one, the one, of the faces of an -simplex. There are three cases:
-
if :
- Let and then for , then satisfies , ;
-
if :
- Let and for , then take , and finally a downwards induction given by , for , then gives for ;
-
if :
- use and for , then satisfies , .
Geometric realization
So far we we have considered passing from topological spaces to simplicial sets by applying the singular simplicial complex functor of def. . Now we discuss a left adjoint of this functor, called geometric realization, which turns a simplicial set into a topological space by identifying each of its abstract n-simplices with the standard topological -simplex.
This is an example of a general abstract phenomenon:
Proposition
Let
be a functor from a small category to a locally small category with all colimits. Then the nerve-functor
has a left adjoint functor , called geometric realization,
given by the coend
(Kan 58)
Example
The singular simplicial complex functor of def. has a left adjoint geometric realization functor
given by the coend
Topological geometric realization takes values in particularly nice topological spaces.
Proposition
The topological geometric realization of simplicial sets in example takes values in CW-complexes.
(e.g. Goerss-Jardine 99, chapter I, prop. 2.3)
Thus for a topological space the adjunction counit of the nerve and realization-adjunction is a candidate for a replacement of by a CW-complex. For this, should be at least a weak homotopy equivalence, i.e. induce isomorphisms on all homotopy groups. Since homotopy groups are built from maps into out of compact topological spaces it is plausible that this works if the topology of is entirely detected by maps out of compact topological spaces into . Topological spaces with this property are called compactly generated.
We take compact topological space to imply Hausdorff topological space.
Definition
A subspace of a topological space is called compactly open or compactly closed, respectively, if for every continuous function out of a compact topological space the preimage is open or closed, respectively.
A topological space is a compactly generated topological space if each of its compactly closed subspaces is already closed.
Write
for the full subcategory of Top on the compactly generated topological spaces.
Often the condition is added that a compactly closed topological space be also a weakly Hausdorff topological space.
Example
Examples of compactly generated topological spaces, def. , include
-
every compact space;
-
every locally compact space;
-
every topological manifold;
-
every CW-complex;
-
every first countable space
Corollary
The topological geometric realization functor of simplicial sets in example takes values in compactly generated topological spaces
Proposition
The subcategory of def. has the following properties
-
It is a coreflective subcategory
The coreflection of a topological space is given by adding to the open subsets of all compactly open subsets, def. .
-
It has all small limits and colimits.
The colimits are computed in , the limits are the image under of the limits as computed in .
-
It is a cartesian closed category.
The cartesian product in is the image under of the Cartesian product formed in .
This is due to (Steenrod 67), expanded on in (Lewis 78, appendix A). One says that prop. with example makes a “convenient category of topological spaces”.
Proposition
Regarded, via corollary as a functor , geometric realization preserves finite limits.
See at Geometric realization is left exact.
Proof idea
The key step in the proof is to use the cartesian closure of (prop. ). This gives that the Cartesian product is a left adjoint and hence preserves colimits in each variable, so that the coend in the definition of the geometric realization may be taken out of Cartesian products.
Lemma
The geometric realization, example , of a minimal Kan fibration, def. is a Serre fibration, def. .
This is due to (Gabriel-Zisman 67). See for instance (Goerss-Jardine 99, chapter I, corollary 10.8, theorem 10.9).
Proof idea
By prop. minimal Kan fibrations are simplicial fiber bundles, locally trivial over each simplex in the base. By prop. this property translates to their geometric realization also being a locally trivial fiber bundle of topological spaces, hence in particular a Serre fibration.
Proposition
The geometric realization, example , of any Kan fibration, def. is a Serre fibration, def. .
This is due to (Quillen 68). See for instance (Goerss-Jardine 99, chapter I, theorem 10.10).
Proposition
For a Kan complex, then the unit of the nerve and realization-adjunction (prop. , example )
is a weak homotopy equivalence, def. .
For any topological space, then the adjunction counit
e.g. (Goerss-Jardine 99, chapter I, prop. 11.1 and p. 63).
Proof idea
Use prop. and prop. applied to the path fibration to proceed by induction.
The classical model structure on simplicial sets
Definition
(classical model structure on simplicial sets)
The classical model structure on simplicial sets, , has the following distinguished classes of morphisms:
-
The classical weak equivalences are the morphisms whose geometric realization, example , is a weak homotopy equivalence of topological spaces;
-
The classical fibrations are the Kan fibrations, def. ;
-
The classical cofibrations are the monomorphisms of simplicial sets, i.e. the degreewise injections.
Proposition
In model structure , def. , the following holds.
-
The fibrant objects are precisely the Kan complexes.
-
A morphism of fibrant simplicial sets / Kan complexes is a weak equivalence precisely if it induces an isomorphism on all simplicial homotopy groups, def. .
-
All simplicial sets are cofibrant with respect to this model structure.
Proposition
The acyclic fibrations in (i.e. the maps that are both fibrations as well as weak equivalences) between Kan complexes are precisely the morphisms that have the right lifting property with respect to all inclusions of boundaries of -simplices into their -simplices
This appears spelled out for instance as (Goerss-Jardine 99, theorem 11.2).
In fact:
Proposition
is a cofibrantly generated model category with
Theorem
Let be the smallest class of morphisms in satisfying the following conditions:
- The class of monomorphisms that are in is closed under pushout, transfinite composition, and retracts.
- has the two-out-of-three property in and contains all the isomorphisms.
- For all natural numbers , the unique morphism is in .
Then is the class of weak homotopy equivalences.
Proof
- First, notice that the horn inclusions and are in .
- Suppose that the horn inclusion is in for all and all . Then for , the horn inclusion is also in .
- Quillen’s small object argument then implies all the trivial cofibrations are in .
- If is a trivial Kan fibration, then its right lifting property implies there is a morphism such that , and the two-out-of-three property implies is a trivial cofibration. Thus every trivial Kan fibration is also in .
- Every weak homotopy equivalence factors as where is a trivial Kan fibration and is a trivial cofibration, so every weak homotopy equivalence is indeed in .
- Finally, noting that the class of weak homotopy equivalences satisfies the conditions in the theorem, we deduce that it is the smallest such class.
As a corollary, we deduce that the classical model structure on is the smallest (in terms of weak equivalences) model structure for which the cofibrations are the monomorphisms and the weak equivalences include the (combinatorial) homotopy equivalences.
Proposition
Let be the connected components functor, i.e. the left adjoint of the constant functor . A morphism in is a weak homotopy equivalence if and only if the induced map
is a bijection for all Kan complexes .
Proof
One direction is easy: if is a Kan complex, then axiomS FOR simplicial model categories (Def. ) implies the functor is a right Quillen functor, so Ken Brown's lemma (Prop. ) implies that it preserves all weak homotopy equivalences; in particular, sends weak homotopy equivalences to bijections.
Conversely, when is a Kan complex, there is a natural bijection between and the hom-set , and thus by the Yoneda lemma, a morphism such that the induced morphism is a bijection for all Kan complexes is precisely a morphism that becomes an isomorphism in , i.e. a weak homotopy equivalence.
Theorem
(Quillen equivalence between classical model structure on topological spaces and classical model structure on simplicial sets)
The singular simplicial complex/geometric realization-adjunction of example constitutes a Quillen equivalence between the classical model structure on simplicial sets of def. and the classical model structure on topological spaces:
Proof
First of all, the adjunction is indeed a Quillen adjunction: prop. says in particular that takes Serre fibrations to Kan fibrations and prop. gives that sends monomorphisms of simplicial sets to relative cell complexes.
Now prop. says that the derived adjunction unit and derived adjunction counit are weak equivalences, and hence the Quillen adjunction is a Quillen equivalence.
Basic notions of higher topos theory
We have discussed basic notions of topos theory above and of homotopy theory (above). The combination of the two is higher topos theory which we discuss here.
We had explained how toposes may be thought of as categories of generalized spaces and how homotopy theory is about relaxing the concept of equality to that of gauge transformation/homotopy and higher gauge transformation/higher homotopy. Accordingly, higher toposes may be thought of as higher categories of generalized spaces whose probe are defined only up to gauge transformation/homotopy. Examples of such include orbifolds and Lie groupoids.
(…)
Locally presentable -Categories
The analog of the notion of locally presentable categories (Def. ) for model categories (Def. ) are combinatorial model categories (Def. ) below. In addition to the ordinary condition of presentability of the underlying category, these are required to be cofibrant generation (Def. below) in that all cofibrations are retracts of relative cell complex-inclusions.
That this is indeed the correct model category-analog of locally presentable categories is the statement of Dugger's theorem (Def. below).
Hence as we pass to the localization of the very large category of combinatorial model categories at the Quillen equivalences, we obtain a homotopy-theoretic refinement of the very large category PrCat of locally presentable categories: Ho(CombModCat) (Def. ). An object in Ho(CombModCat) we also refer to as a locally presentable (∞,1)-category, and a morphism in Ho(CombModCat) we also refer to as the equivalence class of an (∞,1)-colimit-preserving (∞,1)-functor.
Definition
(cofibrantly generated model category)
A model category (def. ) is called cofibrantly generated if there exists two small subsets
of its class of morphisms, such that
-
the (acyclic) cofibrations of are precisely the retracts, of -relative cell complexes (-relative cell complexes), def. .
Proposition
For a cofibrantly generated model category, def. , with generating (acylic) cofibrations (), then its classes of weak equivalences, fibrations and cofibrations are equivalently expressed as injective or projective morphisms (def. ) this way:
-
;
-
;
-
;
Proof
It is clear from the definition that , so that the closure property of prop. gives an inclusion
For the converse inclusion, let . By the small object argument, prop. , there is a factorization . Hence by assumption and by the retract argument lemma , is a retract of an -relative cell complex, hence is in .
This proves the first statement. Together with the closure properties of prop. , this implies the second claim.
The proof of the third and fourth item is directly analogous, just with replaced for .
Definition
(combinatorial model category)
A combinatorial model category is a model category (Def. ) which is
-
locally presentable (Def. )
Example
(classical model structure on simplicial sets is combinatorial model category)
The classical model structure on simplicial sets (Def. ) is a combinatorial model category (Def. ).
Example
(category of simplicial presheaves)
Let be a small (Def. ) sSet-enriched category (Def. with Example ) and consider the enriched presheaf category (Example )
This is called the category of simplicial presheaves on .
By Prop. this is equivalent (Def. ) to the category of simplicial objects in the category of presheaves over (Example ):
This implies for instance that if
a functor, the induced adjoint triple (Remark ) of sSet-enriched functor Kan extensions (Prop. )
is given simplicial-degreewise by the corresponding Set-enriched Kan extensions.
Proposition
(model categories of simplicial presheaves)
Let be a small (Def. ) sSet-enriched category (Def. with Example ). Then the category of simplicial presheaves (Example ) carries the following two structures of a model category (Def. )
-
the projective model structure on simplicial presheaves
has as weak equivalences and fibrations those natural transformations whose component on every object is a weak equivalences or fibration, respectively, in the classical model structure on simplicial sets (Def. );
-
the injective model structure on simplicial presheaves
has as weak equivalences and cofibrations those natural transformations whose component on every object is a weak equivalences or cofibration, respectively, in the classical model structure on simplicial sets (Def. );
Moreover, the identity functors constitute a Quillen equivalence (Def. ) between these two model structures
Remark
The Quillen adjunction (97) in Prop. implies in particular that
-
every projective cofibration is in particular an objectwise cofibration;
-
every injective fibration is in particular an objectwise fibration;
Proposition
(some projectively cofibrant simplicial presheaves)
Let be a small (Def. ). Then a sufficient condition for a simplicial presheaf over (Def. )
to be a cofibrant object with respect to the projective model structure on simplicial presheaves (Prop. ) is that
-
is degreewise a coproduct of representable presheaves
-
the degeneracy maps are inclusions of direct summands.
In particular every representable presheaf, regarded as a simplicially constant simplicial presheaf, is projectively cofibrant.
(Dugger 00, section 9, lemma 2.7)
The following concept of left Bousfield localization is the analog for model categories of the concept of reflection onto local objects (Def. ):
Definition
A left Bousfield localization of a model category (Def. ) is another model category structure on the same underlying category with the same cofibrations,
but more weak equivalences
We say that this is localization at .
Notice that:
Proposition
(left Bousfield localization is Quillen reflection)
Given a left Bousfield localization of as in def. , then the identity functor exhibits a Quillen reflection (Def. )
In particular, by Prop. , the induced adjunction of derived functors (Prop. ) exhibits a reflective subcategory inclusion of homotopy categories (Def. )
Proof
We claim that
-
;
-
;
Using the properties of the weak factorization systems (def.) of (acyclic cofibrations, fibrations) and (cofibrations, acyclic fibrations) for both model structures we get
and
Next to see that the identity functor constitutes a Quillen adjunction (Def. ): By construction, preserves cofibrations and acyclic cofibrations, hence is a left Quillen functor.
To see that the derived adjunction counit (Def. ) is a weak equivalence:
Since we have an adjoint pair of identity functors, the ordinary adjunction counit is the identity morphisms and hence the derived adjunction counit on a fibrant object is just a cofibrant resolution-morphism
but regarded in the model structure . Hence it is sufficient to see that acyclic fibrations in remain weak equivalences in the left Bousfield localized model structure. In fact they even remain acyclic fibrations, bu the first point above.
We may also easily check directly the equivalent statement (via Prop. ) that the induced adjunction of derived functors on homotopy categories is a reflective subcategory-inclusion:
Since the notion of left homotopy in is the same as that in , and hence the inclusion of the subcategory of local cofibrant-fibrant objects into the homotopy category of the original cofibrant-fibrant objects is clearly a full subcategory inclusion. Since by the first statement above, on these cofibrant-fibrant objects the right derived functor of the identity is just the identity and hence does exhibit this inclusion. The left adjoint to this inclusion is given by , by the general properties of Quillen adjunctions (Prop. )).
Proof
We consider the case of left Bousfield localizations, the other case is formally dual.
A left Bousfield localization is a Quillen adjunction by identity functors (this Remark)
This means that the ordinary adjunction counit is the identity morphisms and hence that the derived adjunction counit on a fibrant object is just a cofibrant resolution-morphism
but regarded in the model structure . Hence it is sufficient to see that acyclic fibrations in remain weak equivalences in the left Bousfield localized model structure. In fact they even remain acyclic fibrations, by this Remark.
The following proposition says that Definition of combinatorial model categories is indeed the suitable analog of Def. of locally presentable categories:
Proposition
Let be a combinatorial model category (Def. ). Then there exists
-
a small category ;
-
a small set in its category of simplicial presheaves (Example );
1 a Quillen equivalence (Def. )
between and the left Bousfield localization (Def. ) of the projective model structure on simplicial presheaves over (Prop. ) at the set .
Definition
(homotopy category of presentable (∞,1)-categories)
Write for the very large category whose objects are combinatorial model categories (Def. ) and whose morphisms are left Quillen functors between them (Def. ).
We write
for its localization (Def. ) at the Quillen equivalences (Def. ).
We say:
-
an object in Ho(CombModCat) is a locally presentable (∞,1)-category,
-
a morphism in Ho(CombModCat) is the equivalence class of an(∞,1)-colimit-preserving (∞,1)-functor;
-
an isomorphism in Ho(CombModCat) is an equivalence of (∞,1)-categories.
The following example is the genralization of the category of sets (Def. ) as we pass to homotopy theory:
Example
(∞Grpd)
The image of the classical model structure on simplicial sets (Def. ), which is combinatorial model category by example , under the localization to Ho(CombModCat) (Def. ), we call the presentable (∞,1)-category of ∞-groupoids:
In order to get good control over left Bousfield localization (Def. ) and hence over presentable (∞,1)-categories (Def. ) we need the analog of Prop. , saying that reflective localization are reflections onto their full subcategories of local objects. For this, in turn, we need a good handle on the hom-infinity-groupoids:
Definition
An sSet-enriched model category or simplicial model category, for short is a category (Def. ) equipped with
-
the structure of an sSet-enriched category (Def. via Example ), which is also tensored and cotensored over sSet (Def. )
(with sSet (Def. ), equipped with its canonical structure of a cosmos from Prop. , Example ),
-
the structure of a model category (Def. )
such that these two structures are compatible in the following way:
-
for every cofibration and every fibration in , the induced pullback powering-morphism of hom-simplicial sets
(98)is a Kan fibration (Def. ), and is a weak homotopy equivalence (Def. ) as soon as one of the two morphisms is a weak equivalence in .
Proposition
(in simplicial model category enriched hom-functor out of cofibrant into fibrant is homotopical functor)
Let be a simplicial model category (Def. ).
If is a cofibrant object, then the enriched hom-functor (Example ) out of
preserves fibrations and acyclic fibrations.
If is a fibrant object, then the enriched hom-functor (Example ) into
sends cofibrations and acyclic cofibrations in to fibrations and acyclic fibrations, respectively, in the classical model structure on simplicial sets.
Proof
In the first case, consider the comparison morphism (98) for the initial object, in the second case consider it for the terminal object (Def. )
Since is a tensored and cotensored category, Prop. says that
This means that in the first case the comparison morphism
(98) becomes equal to the top morphism in the following diagram
while in the second case it becomes equal to the left morphism in
Hence the claim follows by the defining condition on the comparison morphism in a simplicial model category.
Definition
Let be a simplicial model category (Def. ).
By Prop. and by Ken Brown's lemma (Prop. ), the enriched hom-functor (Example ) has a right derived functor (Def. ) when its first argument is cofibrant and its second argument is fibrant. The combination is called the derived hom-functor
In view of the Quillen equivalence (Theorem ), the simplicial sets (Kan complexes) are also called the derived hom-spaces.
In the presence of functorial cofibrant resolution and fibrant resolution (Def. ) this is given by the ordinary enriched hom-functor as
Proposition
(recognition of simplicial Quillen adjunctions)
Let and be two simplicial model categories (Def. ) such that is also a left proper model category (Def. ). Then for an sSet-enriched adjunction (Def. ) of the form
to be Quillen adjunction (Def. , hence a simplicial Quillen adjunction) it is sufficient that the following two conditions hold:
-
preserves cofibrations,
-
preserves fibrant objects
(i.e. this already implies that preserves all fibrations).
Proposition
(model structure on simplicial presheaves is left proper combinatorial simplicial model category)
Let be a small (Def. ) sSet-enriched category (Def. with Example ). Then the injective and projective model structure on simplicial presheaves over (Prop. )
are
-
proper model categories (Def. ),
-
simplicial model categories (Def. ),
-
combinatorial model categories (Def. ).
The following is the model category-analog of the concept of local objects from Def. :
Definition
(local objects and local morphisms in a model category)
Let be a simplicial model category (Def. ) and let be a sub-class of its class of morphisms. Then
-
an object is called a (derived-)local object if for every the value of the derived hom-functor (Def. ) out of into is a weak equivalence (i.e. an isomorphism in the classical homotopy category )
-
a morphism in is called a (derived-)local morphism if for every local object we have
The following is the model category-analog of the characterization from Prop. of reflective localizations as reflections onto local objects:
Proposition
(existence of left Bousfield localization for left proper simplicial combinatorial model categories)
Let be a combinatorial model category (Def. ) which is left proper (Def. ) and simplicial (Def. ), and let be a small set of its morphisms.
Then the left Bousfield localization (Def. ) of at , namely at the class of -local morphisms (Def. ) exist, to be denoted , and it has the following properties:
-
is itself a left proper simplicial combinatorial model category;
-
the fibrant objects of are precisely those fibrant objects of which in addition are -local objects (Def. );
-
the homotopy category (Def. ) of is the full subcategory of that of on ( the images under localization of) the -local objects.
The following class of examples of left Bousfield localizations generalizes those of Def. from 1-categories to locally presentable (∞,1)-categories:
Definition
(homotopy localization of combinatorial model categories)
Let be a combinatorial model category (Def. ) which, by Dugger's theorem (Prop. ) is Quillen equivalent to a left Bousfield localization of a model category of simplicial presheaves over some small simplicial category
Let moreover
be any object. Then the homotopy localization of at is the further left Bousfield localization (Def. ) at the morphisms of the form
for all :
The image of this homotopy localization in Ho(CombModCat) (Def. ) we denote by
-Modalities
The following is an homotopy theoretic analog of adjoint triples (Remark ):
Definition
Let be model categories (Def. ), where and share the same underlying category , and such that the identity functor on constitutes a Quillen equivalence (Def. )
Then a Quillen adjoint triple
is a pair of Quillen adjunctions (Def. ), as shown, together with a 2-morphism in the double category of model categories (Def. )
whose derived natural transformation (Def. ) is invertible (a natural isomorphism).
If two Quillen adjoint triples overlap
we speak of a Quillen adjoint quadruple, and so forth.
Proposition
(Quillen adjoint triple induces adjoint triple of derived functors on homotopy categories)
Given a Quillen adjoint triple (Def. ), the induced derived functors (Def. ) on the homotopy categories (Def. ) form an ordinary adjoint triple (Remark ):
Proof
This follows immediately from the fact that passing to homotopy categories of model categories is a double pseudofunctor from the double category of model categories to the double category of squares in Cat (Prop. ).
Example
(Quillen adjoint triple from left and right Quillen functor)
Given an adjoint triple (Remark )
such that is both a left Quillen functor as well as a right Quillen functor (Def. ) for given model category-structures on the categories and . Then this is a Quillen adjoint triple (Def. ) of the form
Proof
The condition of a Quillen equivalence (99) is trivially satisfied (by Prop. ). Similarly the required 2-morphism (100)
exists trivially. To check that its derived natural transformation (Def. ) is a natural isomorphism we need to check (by Prop. ) that for every fibrant and cofibrant object the composite
is a weak equivalence. But this is trivially the case, by definition of fibrant resolution/cofibrant resolution (Def. ; in fact, since is assumed to be both left and right Quillen, also is a fibrant and cofibrant objects and hence we may even take both as well as to be the identity morphism).
The following is the analog in homotopy theory of the adjoint triple of the adjoint triple colimit/constant functor/limit (Def. ):
Example
(Quillen adjoint triple of homotopy limits/colimits of simplicial sets)
Let be a small category (Def. ), and write for the projective/injective model structure on simplicial presheaves over (Prop. ), which participate in a Quillen equivalence of the form
Moreover, the constant diagram-assigning functor
is clearly a left Quillen functor for the injective model structure, and a right Quillen functor for the projective model structure.
Together this means that in the double category of model categories (Def. ) we have a 2-morphism of the form
Moreover, the derived natural transformation (Prop. ) of this square is invertible, if for every Kan complex
is a weak homotopy equivalence (by Prop. ), which here is trivially the case.
Therefore we have a Quillen adjoint triple (Def. ) of the form
The induced adjoint triple of derived functors on the homotopy categories (via Prop. ) is the homotopy colimit/homotopy limit adjoint triple
More generally:
Example
(Quillen adjoint triple of homotopy Kan extension of simplicial presheaves)
Let and be small categories (Def. ), and let
be a functor between them. By Kan extension (Prop. ) enriched over sSet (Example ) this induces an adjoint triple between categories of simplicial presheaves (Def. ):
where
is the operation of precomposition with . This means that preserves all objectwise cofibrations/fibrations/weak equivalences in the model structure on simplicial presheaves (Prop. ). Hence it is
-
a right Quillen functor (Def. ) ;
-
a left Quillen functor (Def. ) ;
and since
is also a Quillen adjunction (Def. ), these imply that is also
In summary this means that we have 2-morphisms in the double category of model categories (Def. ) of the following form:
To check that the corresponding derived natural transformations are natural isomorphisms, we need to check (by Prop. ) that the composites
are invertible in the homotopy category (Def. ), for all fibrant-cofibrant simplicial presheaves in . But this is immediate, since the two factors are weak equivalences, by definition of fibrant/cofibrant resolution (Def. ).
Hence we have a Quillen adjoint triple (Def. ) of the form
The corresponding derived adjoint triple on homotopy categories (Prop. ) is that of homotopy Kan extension:
Example
(Quillen adjoint quadruple of homotopy Kan extension of simplicial presheaves along adjoint pair)
Let and be small categories (Def. ), and let
be a pair of adjoint functors (Def. ). By Kan extension this induces an adjoint quadruple (Prop. ) between categories of simplicial presheaves (Def. )
By Example the top three as well as the bottom three of these form Quillen adjoint triples (Def. ) for model structures on simplicial presheaves (Prop. ) in two ways (101). If for the top three we choose the first version, and for the bottom three the second version from (101), then these combine to a Quillen adjoint quadruple of the form
Example
(Quillen adjoint quintuple of homotopy Kan extension of simplicial presheaves along adjoint triple)
Let and be small categories (Def. ) and let
be a triple of adjoint functors (Remark ). By Kan extension (Prop. ) enriched over sSet (Def. ) this induces an adjoint quintuple between categories of simplicial presheaves
By Example the top four functors in (102) form a Quillen adjoint quadruple (Def. ) on model structures on simplicial presheaves (Prop. ) ending in a right Quillen functor
But here is also a left Quillen functor (as in Example ), and hence this continues by one more Quillen adjoint triple via Example to a Quillen adjoint quintuple of the form
Alternatively, we may regard the bottom four functors in (102) as a Quillen adjoint quadruple via example , whose top functor is then the left Quillen functor
But this is also a right Quillen functor (as in Example ) and hence we may continue by one more Quillen adjoint triple upwards (via Example ) to obtain a Quillen adjoint quintuple, now of the form
We now discuss how to extract derived adjoint modalities from systems of Quillen adjoint triples. First we consider some preliminary lemmas.
Lemma
(derived adjunction units of Quillen adjoint triple)
Consider a Quillen adjoint triple (Def. )
such that the two model structures and on the category share the same class of weak equivalences.
Then:
-
the derived adjunction unit of in (Def. ) differs only by a weak equivalence from the plain adjunction unit (Def. ).
-
the derived adjunction counit of (Def. ) differs only by a weak equivalence form the plain adjunction counit (Def. ).
Proof
By Def. , the derived adjunction unit is on cofibrant objects given by
Here the fibrant resolution-morphism is an acyclic cofibration in . Since is also a left Quillen functor , the comparison morphism is an acyclic cofibration in , hence in particular a weak equivalence in and therefore, by assumption, also in .
The derived adjunction counit of the second adjunction is
Here the cofibrant resolution-morphisms is an acyclic fibration in . Since is also a right Quillen functor , the comparison morphism is an acyclic fibration in , hence in particular a weak equivalence there, hence, by assumption, also a weak equivalence in .
Lemma
(fully faithful functors in Quillen adjoint triple)
Consider a Quillen adjoint triple (Def. )
If and are fully faithful functors (necessarily jointly, by Prop. ), then so are their derived functors and (Prop. ).
Proof
We discuss that being fully faithful implies that is fully faithful. Since also the derived functors form an adjoint triple (by Prop. ), this will imply the claim also for and , by Prop. .
By Lemma the derived adjunction counit of is, up to weak equivalence, the ordinary adjunction counit. But the latter is an isomorphism, since is fully faithful (by this Prop.). In summary this means that the derived adjunction unit of is a weak equivalence, hence that its image in the homotopy category is an isomorphism. But the latter is the ordinary adjunction unit of (by this Prop.), and hence the claim follows again by that Prop..
Lemma
(fully faithful functors in Quillen adjoint quadruple)
Given a Quillen adjoint quadruple (Def. )
if any of the four functors is fully faithful functor, then so is its derived functor.
Proof
Observing that each of the four functors is either the leftmost or the rightmost adjoint in the top or the bottom adjoint triple within the adjoint quadruple, the claim follows by Lemma .
In summary:
Proposition
(derived adjoint modalities from fully faithful Quillen adjoint quadruples)
Given a Quillen adjoint quadruple (Def. )
then the corresponding derived functors form an adjoint quadruple
Moreover, if one of the functors in the Quillen adjoint quadruple is a fully faithful functor, then so is the corresponding derived functor.
Hence if the original adjoint quadruple induces an adjoint modality on (Def. )
or on
then so do the corresponding derived functors on the homotopy categories, respectively.
Proof
The existence of the derived adjoint quadruple followy by Prop. and by uniqueness of adjoints (this Prop.).
The statement about fully faithful functors is Lemma . The reformulation in terms of adjoint modalities is by this Prop.
-Toposes
The characterization of sheaf toposes as the left exact reflective localizations of presheaf toposes (Prop. ) now has an immediate generalization from the realm of locally presentable categories to that of combinatorial model categories and their corresponding locally presentable (∞,1)-categories (Def. ): This yields concept of model toposes and (∞,1)-toposes (Def. below).
Definition
(model topos and (∞,1)-topos)
A combinatorial model category (Def. ) is a model topos if it has a presentation via Dugger's theorem (Prop. )
such that the left derived functor preserves finite homotopy limits.
We denote the image of such a combinatorial model category under the localization functor in Ho(CombModCat) (Def. ) by
and call this an (∞,1)-topos over a site . Moreover, we denote the image of the defining Quillen adjunction (103) in Ho(CombModCat) by
The following construction generalizes the Cech groupoid (Example ) as groupoids are generalized to Kan complexes (Def. ):
Example
Let be a site (Def. ). Then for every object and every covering there is a simplicial presheaf (Example )
which in degree is given by the disjoint union of the -fold fiber products of presheaves over of the patches of the cover, regarded as presheaves under the Yoneda embedding (Prop. )
The face maps are the evident projection morphisms, and the degeneracy maps the evident diagonal morphisms.
This is called the Cech nerve of the given cover.
By the definition of fiber products there is a canonical morphism of simplicial presheaves from the Cech nerve to
We call this the Cech nerve projection.
More generally, for
any morphism of presheaves, there is the correspnding Cech nerve simplicial presheaf
which in degree is the -fold fiber product of with itself:
The following is the generalization of Prop. , saying that Cech nerves are codescent-objects for (∞,1)-sheaves:
Proposition
Let be a site (Def. ) and let
be the set of projections (104) out of the Cech nerves (Example ) for coverings of all objects in the site, as a subset of the class of morphisms of simplicial presheaves over (Example ).
Then the left Bousfield localization (Def. ) of the projective or injective model structure on simplicial presheaves (Prop. ), to be denoted
and to be called the (projective or injective) local model structure on simplicial presheaves, is left exact, in that it exhibits a model topos according to Def. , hence in that its image in Ho(CombModCat) is an (∞,1)-topos
Proposition
(Quillen equivalence between projective and injective topological localization)
Let be a site (Def. ) and let
be the set of projections (104) out of the Cech nerves (Example ) for coverings of all objects in the site, as a subset of the class of morphisms of simplicial presheaves over (Example ).
If each Cech nerve is already a cofibrant object in the projective model structure on simplicial presheaves (prop. ) then the identity functors constitute a Quillen equivalence (Def. ) between the corresponding topological localizations (Def. ) of the projective and the injective model structure on simplicial presheaves:
Proof
First to see that we have a Quillen adjunction (Def. ): By Prop. this is the case before left Bousfield localization. By the nature of left Bousfield localization, and since the model structures are left proper simplicial model categories (by Prop. ), by Prop. it is sufficient to check that the right Quillen functor preserves fibrant objects. By Prop. this means to check that it preserves -local objects. But since is assumed to be projectively cofibrant, and since injectively fibrant objects are already projectively fibrant, the condition on an injectively local object according to Def. is exactly the same as for a projectively local object.
Now to see that this Quillen adjunction is a Quillen equivalence, it is sufficient to check that the corresponding left/right derived functors induce an equivalence of categories on homotopy categories. By Prop. this is the case before left Bousfield localization. By Prop. it is thus sufficient to check that derived functors (before localization) preserves -local objects. By Prop. for this it is sufficient that the Quillen functors themselves preserve local objects. For the right Quillen functor we have just seen this in the previous paragaraph, for the left Quillen functor it follows analogously.
Example
(homotopy localization at over the site of s)
Let be any site (Def. ), and write for its local projective model category of simplicial presheaves (Prop. ).
Assume that contains an object , such that every other object is a finite product , for some . (In other words, assume that is also the syntactic category of Lawvere theory.)
Consider the -homotopy localization (Def. ) of the (∞,1)-sheaf (∞,1)-topos over (Prop. )
hence the left Bousfield localization of model categories
at the set of morphisms
Then this is equivalent (Def. ) to ∞Grpd (Def. ),
in that the (constant functor limit)-adjunction (Def. )
is a Quillen equivalence (Def. ).
Proof
First to see that (105) is a Quillen adjunction (Def. ): Since we have a simplicial Quillen adjunction before localization
(by Example ) and since both model categories here are left proper simplicial model categories (by Prop. and Prop. ), and since left Bousfield localization does not change the class of cofibrations (by Def. ) it is sufficient to show that preserves fibrant objects (by Prop. ).
But by assumption has a terminal object (Def. ), which is hence the initial object of , so that the limit operation is given just by evaluation on that object:
Hence it is sufficient to see that an injectively fibrant simplicial presheaf is objectwise a Kan complex. This is indeed the case, by Prop. .
To check that (105) is actually a Quillen equivalence (Def. ), we check that the derived adjunction unit and derived adjunction counit (Def. ) are weak equivalences:
For any simplicial set (necessarily cofibrant), the derived adjunction unit is
where is a fibrant replacement (Def. ). But is clearly the identity functor and the plain adjunction unit is the identity morphism, so that this composite is just itself, which is indeed a weak equivalence.
For the other case, let be fibrant. This means (by Prop. ) that is fibrant in the injective model structure on simplicial presheaves as well as in the local model structure, and is a derived--local object (Def. ), in that the derived hom-functor out of any into is a weak homotopy equivalence:
But since is fibrant, this derived hom is equivalent to the ordinary hom-functor (Lemma ), and hence with the Yoneda lemma (Prop. ) we have that
is a weak equivalence, for all . By induction on this means that in fact
is a weak equivalence for all . But these are just the components of the adjunction counit
which is hence also a weak equivalence. Hence for the derived adjunction counit
to be a weak equivalence, it is now sufficient to see that the value of a cofibrant replacement on is a weak equivalence. But by definition of the weak equivalences of simplicial presheaves these are objectwise weak equivalences.
Proposition
(Cech nerve-projection of local epimorphism is local weak equivalence)
Let be a site (Def. ) and let
be a local epimorphism (Def. ) in its category of presheaves. Then the corresponding Cech nerve-projection (Def. )
is a weak equivalence in the local projective model structure on simplicial presheaves (Prop. ).
(Dugger-Hollander-Saksen 02, corollary A.3)
Gros -Toposes
We have established above enough higher category theory/homotopy theory that it is now fairly straightforward to generalize the discussion of gros toposes to model toposes/(∞,1)-toposes.
Cohesive -Toposes
The following is a refinement to homotopy theory of the notion of cohesive topos (Def. ):
Definition
An (∞,1)-topos (Def. ) is called a cohesive (∞,1)-topos if it is presented by a model topos (Def. ) which admits a Quillen adjoint quadruple (Def. ) to the classical model category of simplicial sets (Def. ) of the form
such that
-
is a Quillen coreflection (Def. );
-
is a Quillen reflection (Def. );
-
preserves finite products.
The following is the analog of Example :
Example
(Quillen adjoint quadruple on simplicial presheaves over site with finite products)
Let be a small category (Def. ) with finite products (hence with a terminal object and for any two objects their Cartesian product ). By Example the terminal object is witnessed by an adjunction
Consider the category of simplicial presheaves (Example ) with its projective and injective model structure on simplicial presheaves (Prop. ).
Then Kan extension (Prop. ) enriched over sSet (Example ) along the adjoint pair (106) yields a simplicial Quillen adjoint quadruple (Def. )
such that:
-
the functor sends a simplicial presheaf to its simplicial set of global sections, which here is its value on the terminal object:
(108) -
is a Quillen coreflection (Def. )
-
is a Quillen reflection (Def. );
Hence the category of simplicial presheaves over a small category with finite products is a cohesive (∞,1)-topos (Def. ).
Proof
The Quillen adjoint quadruple follows as the special case of Example applied to the adjoint pair
given by inclusion of the terminal object (Example ).
Since the plain adjoint quadruple has a reflective subcategory inclusion and a coreflective subcategory inclusion (Example ) the Quillen (co-)reflection follows by Prop.
The following is a refinement to homotopy theory of the notion of cohesive site (Def. ):
Definition
We call a site (Def. ) ∞-cohesive if the following conditions are satisfied:
-
The category has finite products;
-
For every covering family in the given coverage on , the induced Cech nerve simplicial presheaf (Example ) satisfies the following conditions
-
is a cofibrant object in the projective model structure on simplicial presheaves (Prop. )
-
The simplicial set obtained as the degreewise colimit over the Cech nerve is weakly homotopy equivalent to the point
-
The simplicial set obtained at the degreewise limit over the Cech nerve is weakly homotopy equivalent to the underlying set of points of :
-
The following is the analog of Prop. :
Proposition
(model topos over ∞-cohesive site is cohesive model topos)
Let be an ∞-cohesive site (Def. ). Then the (∞,1)-topos (Def. ) over it, obtained by topological localization (Prop. ) is a cohesive (∞,1)-topos (Def. ).
Proof
By Example we have the required Quillen adjoint quadruple on the projective model structure on simplicial presheaves, i.e. before left Bousfield localization at the Cech nerve projections
Hence it remains to see that these Quillen adjunctions pass to the local model structures from Prop. , and that and then still participate in Quillen (co-)reflections.
By Prop. and Prop. all model structures involved are left proper simplicial model categories, and hence we may appeal to Prop. for recognition of the required Quillen adjunctions. Since, moreover, left Bousfield localization does not change the class of cofibrations (Def. ), this means that we are reduced to checking that all right Quillen functors in the above global Quillen adjoint quadruple preserve fibrant objects with respect to the local model structure.
For the Quillen adjunctions
this means to check that for every Kan complex the simplicial presheaves and are derived-local objects (Def. , Prop. ) with respect to the Cech nerve projections. Since and are right Quillen functors with respect to the global model projective model structure, and are globally projectively fibrant simplicial presheaves. Since, moreover, is projectively cofibrant by assumption, and since the representables are projectively cofibrant by Prop. , the value of the derived hom-functor reduces to that of the ordinary enriched hom-functor (Def. ), and hence the condition is that
are weak equivalences. But now by the ordinary adjunction hom-isomorphism (10), these are identified with
Since the colimit of a representable is the singleton (Lemma ) and since the limit over the opposite of a category with terming object is evaluation at that object, this in turn is equivalent to
Here we recognize the internal hom in simplicial sets from the weak equivalences of the definition of an ∞-cohesive site (Def. ), which necessarily go between cofibrant simplicial sets, into a fibrant simplicial set . Hence this is the derived hom-functor (Def. ) in the classical model structure on simplicial sets. Since the latter is a simplicial model category (Def. ) by Prop. , these morphisms are indeed weak equivalences of simplicial sets.
This establishes that and descent to Quillen adjunctions on the local model structure. Finally, it is immediate that preserves fibrant objects, and hence also passes to the local model structure.
The following is the analog in homotopy theory of the cohesive adjoint modalities from Def. :
Definition
(adjoint triple of derived adjoint modal operators on homotopy category of cohesive model topos)
Given a cohesive model topos (Def. ), its adjoint quadruple (Remark ) of derived functor between homotopy categorues (via Prop. )
induce, by composition of functors, an adjoint triple (Remark ) of adjoint modalities (via Prop. ):
Since and are fully faithful functors by assumption, these are (co-)modal operators (Def. ), (by Prop. and Prop. ).
We pronounce these as follows:
| shape modality | flat modality | sharp modality |
|---|---|---|
and we refer to the corresponding modal objects (Def. ) as follows:
-
is called a discrete object;
-
is called a codiscrete object;
-
is a concrete object.
Elastic -Toposes
The following is a refinement to homotopy theory of the notion of elastic topos (Def. ):
Definition
Given a cohesive model topos (Def. ), a differentially cohesive or elastic model topos over it is another cohesive model topos equipped with a system of Quillen adjoint quadruples (Def. ) of the form
such that
-
is a Quillen coreflection (Def. );
-
is a Quillen reflection (Def. ).
Definition
For an ∞-cohesive site (Def. ), an infinitesimal neighbourhood site of is a coreflective subcategory-inclusion into another ∞-cohesive site
such that
-
the left Kan extension of preserves fiber products of morphisms in a covering ;
-
if is a covering family in , and is any morphism in , then there is a covering familiy such that for all there is a and a commuting square of the form
(110)
We also call this an ∞-elastic site, for short.
Proposition
(model topos over ∞-elastic site is elastic model topos)
Let
be an ∞-elastic site (Def. ). Then Kan extension (Prop. ) enriched over sSet (Example ) induces on the corresponding cohesive model toposes (Prop. ) the structure of an elastic model topos (Def. ).
Proof
By Example we have a Quillen adjoint quadruple for the global projective model structure on simplicial presheaves of the form
Here we denote left Kan extension along a functor by the same symbol as that functor, which is consistent by Prop. .
By Prop. all model categories appearing here are left proper simplicial model categories, and by Def. left Bousfield localization retains the class of cofibrations. Therefore Prop. says that to see that this is also a Quillen adjoint quadruple for the local model structure on simplicial presheaves (Prop. ) it is sufficient that, for each Quillen adjunction, the right adjoint preserves fibrant objects, hence Cech-local objects (Def. ).
For each right adjoint here this means to consider any covering (either in or in ) with induced Cech nerve (Example ) and to check that for a fibrant object in the global projective/injective model structure on simplicial presheaves, that
is a weak equivalence. Notice that this is indeed already the image under the correct derived hom-functor, Def. , since both sites are assumed to be ∞-cohesive sites (Def. ), which means in particular that is projectively cofibrant, and hence also injectively cofibrant, by Prop. .
Now by the enriched adjunction-isomorphism (47) this means equivalently that
is a weak equivalence. This we now check in each of the three cases:
For the case we have that
by the assumption that preserves fiber products of Yoneda embedding-images of morphisms in a covering. Moreover, by the assumption that preserves covering-families, is itself the Cech nerve of a covering family, and hence (111) is a weak equivalence since is assumed to be a local object.
The same argument directly applies also to , where now the respect of for fiber products follows already from the fact that this is a right adjoint (since right adjoints preserve limits, Prop. ).
In the same way, for we need to check that is a weak equivalence. Now is no longer a left Kan extension, hence is no longer a morphism of representable presheaves. But the third assumption (110) on an -elastic site manifestly means, under the adjunction isomorphism (10) for that is a local epimorphism (Def. ). Therefore Prop. implies that
is a weak equivalence. With this, the fact (Prop. with Prop. ) that is a simplicial model category (Def. ) implies that is a weak equivalence.
The following is a refinement to homotopy theory of the adjoint modalities on an elastic topos from Def. :
Definition
(derived adjoint modalities on elastic model topos)
Given an elastic model topos (def. ), composition composition of the derived functors (Prop. ) yields via Prop. and Prop. , the following adjoint modalities (Def. ) on the homotopy category (Def. )
Since and are fully faithful functors by assumption, these are (co-)modal operators (Def. ) on the cohesive topos, by (Prop. ^{op}, sSet]_{loc}) } and Prop. ).
We pronounce these as follows:
| reduction modality | infinitesimal shape modality | infinitesimal flat modality |
|---|---|---|
and we refer to the corresponding modal objects (Def. ) as follows:
-
is called a reduced object;
-
an infinitesimal shape-modal object
is called a coreduced object.
Proposition
(progression of derived adjoint modalities on elastic model topos)
Let be an elastic model topos (Def. ) and consider the corresponding derived adjoint modalities which it inherits
-
for being a cohesive topos, from Def. ,
-
for being an elastic topos, from Def. :
| shape modality | flat modality | sharp modality |
|---|---|---|
| reduction modality | infinitesimal shape modality | infinitesimal flat modality |
Then these arrange into the following progression, via the preorder on modalities from Def.
where we display also the bottom adjoint modality (Example ), for completeness.
Solid -Toposes
The following is a refinement to homotopy theory of the notion of solid topos (Def. ):
Definition
Given an elastic model topos (Def. ) a solid model topos over it is another elastic model topos and a system of Quillen adjoint quadruples (Def. ) as follows
such that
-
is a Quillen reflection (def. );
-
is a Quillen coreflection.
Definition
For an ∞-elastic site (Def. ) over an ∞-cohesive site (Def. ), a super-infinitesimal neighbourhood site is a reflective/coreflective subcategory-inclusion into another ∞-elastic site
such that
-
the left Kan extension of preserves fiber products of morphisms in a covering ;
Proposition
(model topos over ∞-solid site is solid model topos)
Let
be an ∞-solid site (Def. ). Then Kan extension (Prop. ) enriched over sSet (Example ) induces on the corresponding elastic model toposes (Prop. ) the structure of a solid model topos (Def. ).
The following is a refinement to homotopy theory of the modal operators on a solid topos from Def. :
Definition
(derived adjoint modalities on solid model topos)
Given a solid model topos (Def. ), composition of derived functors via Prop. and Prop. , the following adjoint modalities (Def. )
Since and are fully faithful functors by assumption, these are (co-)modal operators (Def. ) on the cohesive topos, by (Prop. and Prop. ).
We pronounce these as follows:
| fermionic modality | bosonic modality | rheonomy modality |
|---|---|---|
and we refer to the corresponding modal objects (Def. ) as follows:
-
is called a bosonic object;
-
a -modal object
is called a rheonomic object;
Proposition
(progression of adjoint modalities on solid topos)
Let be a solid model topos (Def. ) and consider the adjoint modalities which it inherits
-
for being a cohesive topos, from Def. ,
-
for being an elastic topos, from Def. ,
-
for being a solid topos, from Def. :
| shape modality | flat modality | sharp modality |
|---|---|---|
| reduction modality | infinitesimal shape modality | infinitesimal flat modality |
| fermionic modality | bosonic modality | rheonomy modality |
Then these arrange into the following progression, via the preorder on modalities from Def. :
where we are displaying, for completeness, also the adjoint modalities at the bottom and the top (Example ).
(…)
-
“the universality of the concept of adjointness, which was first isolated and named in the conceptual sphere of category theory” (Lawvere 69) “In all those areas where category theory is actively used the categorical concept of adjoint functor has come to play a key role.” (first line from An interview with William Lawvere, paraphrasing the first paragraph of Taking categories seriously) ↩
Last revised on May 1, 2025 at 10:22:57. See the history of this page for a list of all contributions to it.