nLab
simplex

Idea

The cellular simplex is one of the basic geometric shapes for higher structures.

Definition

Cellular (simplicial) simplex

For $n\in \mathbb{N}$, the standard simplicial $n$-simplex is the simplicial set which is represented (as a presheaf) by the object $[n]$ in the simplex category.

Likewise, there is a standard toplogical $n$-simplex, which is (more or less by definition) the geometric realization of the standard simplicial $n$-simplex.

Topological simplex

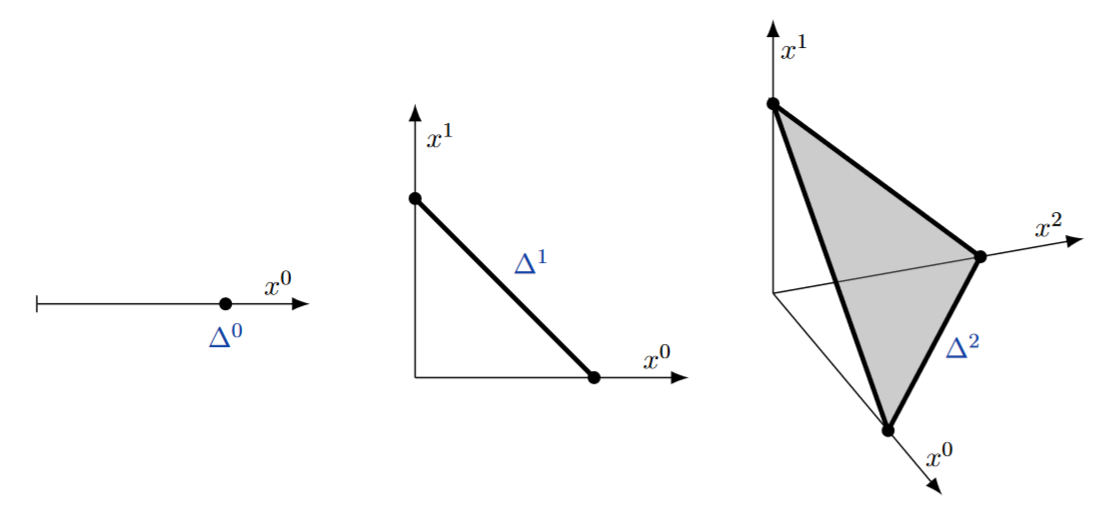
The topological $n$-simplex ${\Delta }^n$ is a generalization of the standard filled triangle in the plane, from dimension 2 to arbitrary. Each ${\Delta }^n$ is homeomorphic to the closed $n$-ball $D^n$, but its defining embedding into a Cartesian space equips its boundary with its cellular decomposition into faces, generalizing the way that the triangle has three edges (which are 1-simplices) as faces, and three points (which are 0-simplices) as corners.

The topological $n$-simplex is naturally defined as a subspace of a Cartesian space given by some relation on its canonical coordinates. There are two standard choices for such coordinate presentation, which of course define homeomorphic $n$-simplices:

• Barycentric coordinates

• Cartesian coordinates

Each of these has its advantages and disadvantages, depending on aplication. But of course there is a simple coordinate transformation that exhibits an explicit homeomorphism between the two:

• Transformation between Barycentric and Cartesian coordinates.

Barycentric coordinates

In the following, for $n\in \mathbb{N}$ we regard the Cartesian space ${ℝ}^n$ as equipped with the canonical coordinates labeled $x_0,x_1,\cdots ,x_{n-1}$.

Definition

For $n\in \mathbb{N}$, the topological $n$-simplex is, up to homeomorphism, the topological space whose underlying set is the subset

$${\Delta }^n≔\{\stackrel{\rightharpoonup }{x}\in {ℝ}^{n+1}\mid \sum _{i=0}^n{x}_i=1\mathrm{and}\forall i.x_i\ge 0\}\subset {ℝ}^{n+1}$$\Delta^n \coloneqq \{ \vec x \in \mathbb{R}^{n+1} | \sum_{i = 0 }^n x_i = 1 \; and \; \forall i . x_i \geq 0 \} \subset \mathbb{R}^{n+1}

of the Cartesian space ${ℝ}^{n+1}$, and whose topology is the subspace topology induces from the canonical topology in ${ℝ}^{n+1}$.

Definition

For $n\in \mathbb{N}$, $n\ge 1$ and $0\le k\le n$, the $k$th $(n-1)$-face (inclusion) of the topological $n$-simplex is the subspace inclusion

$${\delta }_k:{\Delta }^{n-1}\hookrightarrow {\Delta }^n$$\delta_k : \Delta^{n-1} \hookrightarrow \Delta^n

induced under the barycentric coordinates of def. 1, by the inclusion

$${ℝ}^n\hookrightarrow {ℝ}^{n+1}$$\mathbb{R}^n \hookrightarrow \mathbb{R}^{n+1}

which omits the $k+1$st canonical coordinate

$$(x_1,\cdots ,x_n)\mapsto (x_1,\cdots ,x_{k-1},0,x_k,\cdots ,x_n).$$(x_1, \cdots , x_n) \mapsto (x_1, \cdots, x_{k-1} , 0 , x_k, \cdots, x_n) \,.

Example

The inclusion

$${\delta }_0:{\Delta }^0\to {\Delta }^1$$\delta_0 : \Delta^0 \to \Delta^1

is the inclusion

$$\{1\}\hookrightarrow [0,1]$$\{1\} \hookrightarrow [0,1]

of the “right” end of the standard interval. The other inclusion

$${\delta }_1:{\Delta }^0\to {\Delta }^1$$\delta_1 : \Delta^0 \to \Delta^1

is that of the “left” end $\{0\}\hookrightarrow [0,1]$.

Definition

For $n\in \mathbb{N}$ and $0\le k\le n$ the $k$th degenerate $n$-simplex (projection) is the surjective map

$${\sigma }_k:{\Delta }^n\to {\Delta }^{n-1}$$\sigma_k : \Delta^{n} \to \Delta^{n-1}

induced under the barycentric coordinates of def. 1 under the surjection

$${ℝ}^{n+1}\to {ℝ}^n$$\mathbb{R}^{n+1} \to \mathbb{R}^n

which sends

$$(x_0,\cdots ,x_n)\mapsto (x_0,\cdots ,x_k+x_{k+1},\cdots ,x_n).$$(x_0, \cdots, x_n) \mapsto (x_0, \cdots, x_{k} + x_{k+1}, \cdots, x_n) \,.

Proposition

The collection of face inclusions, def. 2 and degenracy projections, def. 3 satisfy the (dual) simplicial identities. Equivalently, they constitute the components of a functor

$${\Delta }^{•}:\Delta \to \mathrm{Top}$$\Delta^\bullet : \Delta \to Top

from the simplex category $\Delta$ to the category Top of topological spaces. This is, up to isomorphism, the canonical cosimplicial object in $\mathrm{Top}$.

Cartesian coordinates

Definition

The standard topological $n$-simplex is, up to homeomorphism, the subset

$${\Delta }^n≔\{\stackrel{\rightharpoonup }{x}\in {ℝ}^n\mid 0\le x_1\le \cdots \le x_n\le 1\}\hookrightarrow {ℝ}^n$$\Delta^n \coloneqq \{ \vec x \in \mathbb{R}^n | 0 \leq x_1 \leq \cdots \leq x_n \leq 1 \} \hookrightarrow \mathbb{R}^n

equipped with the subspace topology of the standard topology on the Cartesian space ${ℝ}^n$.

Remark

This definition identifies the topological $n$-simplex with the space of interval maps (preserving top and bottom) $\{0<1<\dots <n+1\}\to I$ into the topological interval. This point of view takes advantage of the duality between the simplex category $\Delta$ and the category $\nabla$ of finite intervals with distinct top and bottom. Indeed, it follows from the duality that we obtain a functor

$$\Delta \simeq {\nabla }^{\mathrm{op}}\stackrel{\mathrm{Int}(-,I)}{\to }\mathrm{Top}.$$\Delta \simeq \nabla^{op} \stackrel{Int(-, I)}{\to} Top.

Example

• For $n=0$ this is the point, ${\Delta }^0=*$.

• For $n=1$ this is the standard interval object ${\Delta }^1=[0,1]$.

• For $n=2$ this is a triangle sitting in the plane like this:

  $$\{(x_0,x_1)\mid 0\le x_0\le x_1\le 1\}=\left\{\begin{array}{ccccc}& & & & (1,1)\\ & & & \nearrow & \downarrow \\ & & (\frac{1}{2},\frac{1}{2})& & (\frac{1}{2},1)\\ & \nearrow & & & \downarrow \\ (0,0)& \stackrel{}{\to }& (0,\frac{1}{2})& \to & (0,1)\end{array}\right\}$$\left\{ (x_0,x_1) | 0 \leq x_0 \leq x_1 \leq 1 \right\} = \left\{ \array{ && && (1,1) \\ && & \nearrow & \downarrow \\ && (\tfrac{1}{2}, \tfrac{1}{2}) && (\tfrac{1}{2},1) \\ & \nearrow & && \downarrow \\ (0,0) &\stackrel{}{\to}& (0,\tfrac{1}{2}) & \to & (0,1) } \right\}

Transformation between Barycentric and Cartesian coordinates

For $n\in \mathbb{N}$, write now explicitly

$${\Delta }_{\mathrm{bar}}^n\hookrightarrow {ℝ}^{n+1}$$\Delta^n_{bar} \hookrightarrow \mathbb{R}^{n+1}

for the topological $n$-simplex in barycentric coordinate presentation, def. 1, and

$${\Delta }_{\mathrm{cart}}^n\hookrightarrow {ℝ}^n$$\Delta^n_{cart} \hookrightarrow \mathbb{R}^{n}

for the topological $n$-simplex in Cartesian coordinate presentation, def. 4.

Write

$$S_n:{ℝ}^{n+1}\to {ℝ}^n$$S_n : \mathbb{R}^{n+1} \to \mathbb{R}^n

for the continuous function given in the standard coordinates by

$$(x_0,\cdots ,x_n)\mapsto (x_0,x_0+x_1,\cdots ,\sum _{i=0}^k{x}_i,\cdots ,\sum _{i=0}^n{x}_i).$$(x_0, \cdots, x_{n}) \mapsto (x_0, x_0 + x_1, \cdots, \sum_{i = 0}^k x_i, \cdots, \sum_{i = 0}^n x_i) \,.

By restriction, this induces a continuous function on the topological $n$-simplices

$$\begin{array}{ccc}{\Delta }_{\mathrm{bar}}^n& \hookrightarrow & {ℝ}^{n+1}\\ {\downarrow }^{S_n{\mid }_{{\Delta }_{\mathrm{bar}}^n}}& & {\downarrow }^{p_n}\\ {\Delta }_{\mathrm{cart}}^n& \hookrightarrow & {ℝ}^n\end{array}.$$\array{ \Delta^n_{bar} &\hookrightarrow& \mathbb{R}^{n+1} \\ \downarrow^{\mathrlap{S_n|_{\Delta^n_{bar}}}} && \downarrow^{p_n} \\ \Delta^n_{cart} &\hookrightarrow& \mathbb{R}^n } \,.

Proposition

For every $n\in \mathbb{N}$ the function $S_n$ is a homeomorphism and respects the face and degenracy maps.

Equivalently, $S_{•}$ is a natural isomorphism of functors ${\Delta }^n\to \mathrm{Top}$, hence an isomorphism of cosimplicial objects

$$S_{•}:{\Delta }_{\mathrm{bar}}^{•}\stackrel{\simeq }{\to }{\Delta }_{\mathrm{cart}}^{•}.$$S_\bullet : \Delta^\bullet_{bar} \stackrel{\simeq}{\to} \Delta^\bullet_{cart} \,.

Singular simplex

Definition

For $X\in$ Top and $n\in \mathbb{N}$, a singular $n$-simplex in $X$ is a continuous map

$$\sigma :{\Delta }^n\to X.$$\sigma : \Delta^n \to X \,.

Write

$$(\mathrm{Sing}X{)}_n≔{\mathrm{Hom}}_{\mathrm{Top}}({\Delta }^n,X)$$(Sing X)_n \coloneqq Hom_{Top}(\Delta^n , X)

for the set of singular $n$-simplices of $X$.

As $n$ varies, this forms the singular simplicial complex of $X$.

Properties

Relation to globes

The orientals related simplices to globes.

Related concepts

• vertex, edge

• triangle, tetrahedron

• horn, boundary of a simplex, spine

• globe,

• tree, dendrex