nLab vector bundle

Idea

Given some context of geometry, then a vector bundle is a collection of vector spaces that varies in a geometric way over a given base space $X$: over each element $x \in X$ there is a vector space $V_x$, called the fiber over $x$, and as $x$ varies in $X$, the fibers vary along in a geometric way. One also says that vector bundles are fiber bundles whose fiber carries vector space-structure. Hence the theory of vector bundles is parameterized linear algebra. The vector bundles over a fixed base $X$ form a category $VectBund_X$, and as the base space is allowed to vary these fit into a global category VectBund.

For example

• in topology a topological vector bundle is a collection of vector spaces which “vary continuously” over a topological space $X$,

• in differential geometry a differentiable vector bundle is a collection of vector space which “varies differentiably” over a differentiable manifold,

• in algebraic geometry an algebraic vector bundle is a collection of vector spaces which vary algebraically over a scheme.

and so on.

One requires that “locally”, on small enough patches of the base space $X$, the variation of the fibers is constant up to isomorphism (one says the vector bundle is “locally trivial”), but the key point of vector bundles is that there may be non-trivial structure in how the collection of vector spaces “globally glues together”.

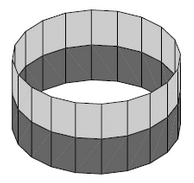
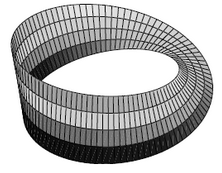
For example if $X = S^1$ is the circle regarded as a topological space in the standard way, and if we consider real vector spaces, then there are up to isomorphism two different $\mathbb{R}$-vector bundles over $S^1$ whose fibers look like the 1-dimensional real vector space $\mathbb{R}$ itself, namely

1. the cylinder

   

2. the Möbius strip:

   

(In these pictures each vertical interval is to be thought of as a stand-in for a copy of the real line $\mathbb{R}$.)

Clearly for the cylinder nothing special happens to the fibers as one moves around the circle (one says this is a trivial vector bundle) while the Möbius strip is “locally trivial” but globally has a twist: as one moves once around the circle the original fiber comes back identified with its reflection at the origin.

graphics grabbed from Hatcher

An important class of examples of vector bundles are tangent bundles of differentiable manifolds $X$. Here the vector space at each point of $X$ is the tangent space of that point, the space of all tangent vectors based at that point. The graphics on the right shows one of the tangent space of the 2-sphere.

Dually, given an embedding of differentiable manifolds into a Euclidean space, then the normal vectors to the tangent bundle span a vector bundle called the normal bundle of the embedding.

All the usual operations on finite dimensional vector spaces in linear algebra generalize to vector bundles by applying them fiber-wise. For instance there is direct sum of vector bundles and the tensor product of vector bundles over the same base space.

To the extent that the base space $X$ is encoded in its algebra of functions (tautologically in algebraic geometry or via Gelfand duality in topology), the Serre-Swan theorem asserts that vector bundles over $X$ are equivalently encoded in the projective modules over these algebras constituted by their sections.

Vector bundles have various applications and uses:

1. their Grothendieck group under direct sum of vector bundles yields topological K-theory, an interesting generalized (Eilenberg-Steenrod) cohomology theory;

2. a reduction of the structure group of vector bundles encodes actual geometry on the base space; when applied to tangent bundles such G-structures on vector bundles encode for instance orthogonal structure, Riemannian geometry, complex geometry, symplectic geometry, conformal geometry etc. (in general: Cartan geometry); when applied to normal bundles these G-structures give rise, via Thom's theorem, to Thom spectra and cobordism theory;

3. equipping differentiable vector bundles with connection on a vector bundle is the basis for Chern-Weil theory and for the application of vector bundles in physics, where they model gauge fields and instanton sectors; see also at fiber bundles in physics.

Definition

Standard

See at topological vector bundle

Sheaf-theoretic version

Vector bundles can also be defined via sheaf theory, which permits easy transport to general Grothendieck toposes. Let $Sh(X)$ be the category of (set-valued) sheaves on $X$. The sheaf of continuous local sections of the product projection

$$X \times \mathbb{R} \to X$$

forms a local ring object $R$; when interpreted in the internal logic of $Sh(X)$, it is the Dedekind real numbers object. Then, according to a theorem of Richard Swan, in its sheaf-theoretic incarnation a vector bundle is the same thing as a projective R-module.

• A theorem of Kaplansky states “every projective module over a local ring is free”. When interpreted in sheaf semantics? (Kripke-Joyal semantics), the existential quantifier implicit in “free” is interpreted locally, so we can consider a vector bundle as a locally free module over the Dedekind reals.

Virtual vector bundles

In one class of models for K-theory – generalized (Eilenberg-Steenrod) cohomology theory – cocycles are represented by $\mathbb{Z}_2$-graded vector bundles (pairs of vector bundles, essentially) modulo a certain equivalence relation. In that context it is sometimes useful to consider a certain variant of infinite-dimensional $\mathbb{Z}_2$-graded vector bundles called vectorial bundles.

Much else to be discussed…

Examples

• canonical bundle

• valence bundle

• …

Related concepts

• principal bundle, associated bundle

• vector bundle:

  • VectBund(X), VectBund

  • real vector bundle

  • complex vector bundle

    • holomorphic vector bundle, pseudoholomorphic vector bundle

  • universal vector bundle

  • rank of a vector bundle

  • dual vector bundle

  • module bundle

  • direct sum of vector bundles

  • short exact sequence of vector bundles

  • connection on a vector bundle

  • flat vector bundle

  • real vector bundle, complex vector bundle

  • super vector bundle

• measurable field of Hilbert spaces

• 2-vector bundle

• (∞,1)-vector bundle / (∞,n)-vector bundle

Literature

• Glenys Luke, Alexandr S. Mishchenko, Vector bundles and their applications, Math. and its Appl. 447 Kluwer (1998) [doi:10.1007/978-1-4757-6923-4, MR99m:55019]

• А. С. Мищенко, Векторные расслоения и их применения (Russian; A. S. Mishchenko, Vector bundles and their applications) Nauka, Moscow, 1984. 208 pp.

• Howard Osborn, Vector bundles. Vol. 1. Foundations and Stiefel-Whitney classes, Pure and Appl. Math. 101, Academic Press 1982. xii+371 pp. MR85e:55001

• Dale Husemöller, Fibre bundles, McGraw-Hill 1966 (300 p.); Springer GTM 1975 (327 p.), 1994 (353 p.).

• Dale Husemöller, Michael Joachim, Branislav Jurco, Martin Schottenloher, Basic Bundle Theory and K-Cohomology Invariants,

  Lecture Notes in Physics, Springer 2008 (pdf)

An exposition with an eye towards gauge theory is in section 16.1 of

• Theodore Frankel, The Geometry of Physics - An Introduction

• Raoul Bott, Loring Tu, Differential forms in algebraic topology, Graduate Texts in Mathematics 82, Springer 1982. xiv+331 pp.

Discussion with an eye towards K-theory is in

• Max Karoubi, K-theory. An introduction, Grundlehren der Mathematischen Wissenschaften 226, Springer 1978. xviii+308 pp.

• Allen Hatcher, Vector bundles and K-Theory, (partly finished book) web