nLab STU relation
Context
Knot theory
Examples/classes:
Types
Related concepts:
Contents
Idea
In knot theory, by the STU-relations, one means the following relations in the linear span of Jacobi diagrams:
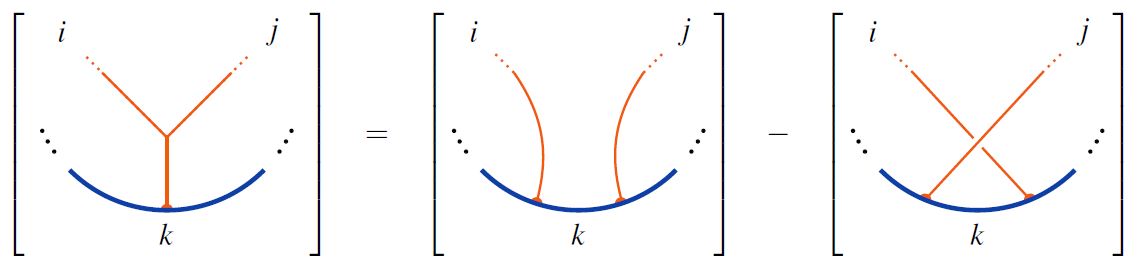
graphics from Sati-Schreiber 19c
Properties
Relation to weight systems and Lie algebra objects
By definition, the STU-relations are the relations respected by weight systems on Jacobi diagrams.
When regarded as relations of string diagrams, the STU relations characterize the Jacobi identity for Lie algebra objects, or more generally the Lie action property of Lie modules:
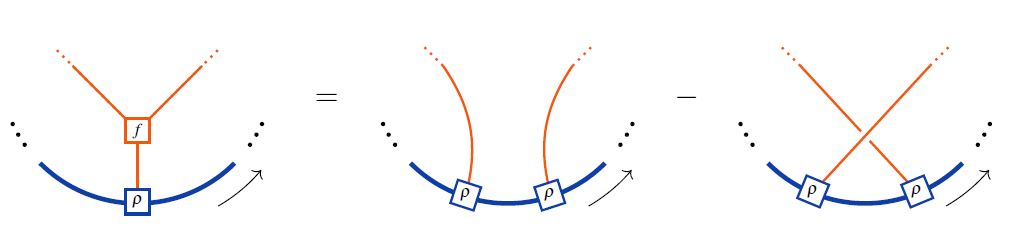
This is the reason behind the existence of Lie algebra weight systems.
Relation to 4T-relations
Under the embedding of the set of round chord diagrams into the set of Jacobi diagrams, the STU-relations imply the 4T relations on round chord diagrams:
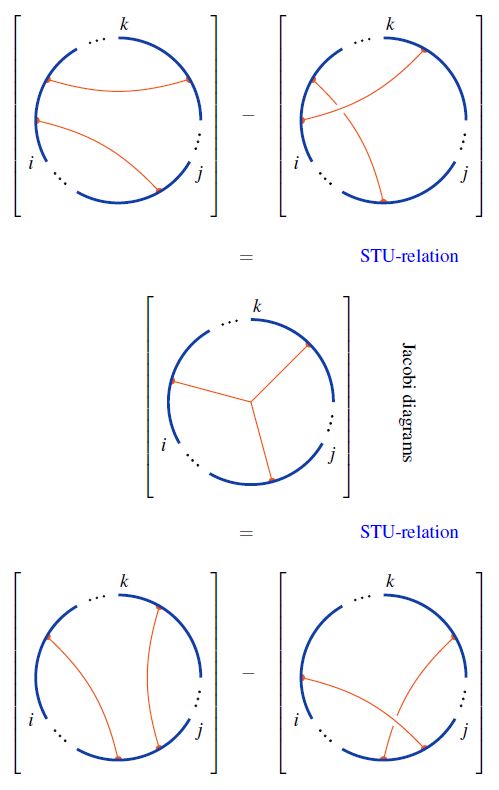
Using this, one finds that chord diagrams modulo 4T are Jacobi diagrams modulo STU:
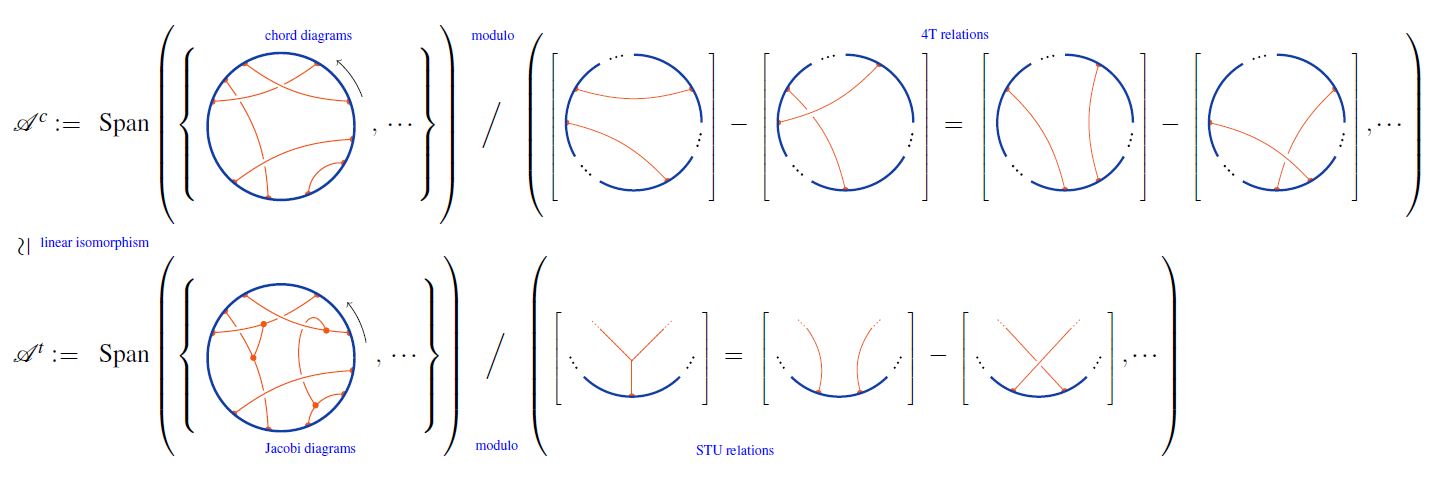
graphics from Sati-Schreiber 19c
Relation to knot-graph complex
That the STU-relations characterize the cochain cohomology of the knot-graph complex in the respective degrees is shown in Koytcheff-Munson-Volic 13, Section 3.4

graphics grabbed from Koytcheff-Munson-Volic 13
Related concepts
References
General
Original articles:
- Dror Bar-Natan, Def. 1.9 in: On the Vassiliev knot invariants, Topology Volume 34, Issue 2, April 1995, Pages 423-472 (doi:10.1016/0040-9383(95)93237-2, pdf)
Textbook accounts:
-
Sergei Chmutov, Sergei Duzhin, Jacob Mostovoy, Section 4 of: Introduction to Vassiliev knot invariants, Cambridge University Press, 2012 (arxiv/1103.5628, doi:10.1017/CBO9781139107846)
-
David Jackson, Iain Moffat, Section 11 of: An Introduction to Quantum and Vassiliev Knot Invariants, Springer 2019 (doi:10.1007/978-3-030-05213-3)
Lecture notes:
- Dror Bar-Natan, Alexander Stoimenow, The Fundamental Theorem of Vassiliev Invariants (arXiv:q-alg/9702009)
In terms of the knot-graph complex
In terms of the knot-graph complex:
- Robin Koytcheff, Brian A. Munson, Ismar Volić, Section 3.4 of: Configuration space integrals and the cohomology of the space of homotopy string links, J. Knot Theory Ramif. 22, no. 11, 73 pp. (2013) (arXiv:1109.0056)
Last revised on December 20, 2019 at 19:32:56. See the history of this page for a list of all contributions to it.