nLab weight system

Idea

In knot theory a framed weight system is an assignment of numbers to chord diagrams that is invariant under the 4T-relation.

If the assignment is in addition invariant under the 1T-relation, then it is called an unframed weight system, or just weight system, for short.

Similarly, in braid group-theory, a horizontal weight system is an assignment of numbers to horizontal chord diagrams that is invariant under the horizontal 2T relation and horizontal 4T relation.

Definition

Round weight systems

Definition

(linear span of chord diagrams modulo 4T)

Let $k$ be a field (or just a commutative ring). Write

1. $\mathcal{D}^c$ for the set of chord diagrams,

2. $k\langle \mathcal{D}^c\rangle$ for its $k$-linear span,

3. $\mathcal{A}^c \;\coloneqq\; k\langle \mathcal{D}^c\rangle/4T$ for the quotient vector space by the 4T-relations.

Definition

(framed weight system)

A $k$-valued framed weight system is a linear function on the linear span of chord diagrams modulo 4T-relations (Def. )

$$w \;\colon\; \mathcal{A}^c \longrightarrow k \,,$$

hence the $k$-vector space of framed weight systems is the dual vector space

$$\mathcal{W} \;\coloneqq\; (\mathcal{A}^c)^\ast$$

(Bar-Natan 95, Def. 1.6, see Chmutov-Duzhin-Mostovoy 11, Def. 4.1.1, Jackson-Moffat 19, Section 11.7)

Remark

Since chord diagrams modulo 4T are Jacobi diagrams modulo STU, framed weight systems equivalently form the dual vector space

(1)$$\begin{aligned} \overset{ \mathclap{ \color{blue} { {framed} \atop {{weight}\atop{systems}} } } }{ \mathcal{W} } & \;\coloneqq\; \big( \overset { \color{blue} { { {chord} \atop {diagrams} } \atop { {modulo}\,{4T} } } } { \mathcal{A}^c } \big)^\ast \\ & \;\simeq\; \big( \underset{ \color{blue} { { {Jacobi} \atop {diagrams} } \atop { {modulo}\,{STU} } } }{ \mathcal{A}^t } \big)^\ast \end{aligned}$$

of the quotient vector space $\mathcal{A}^t \coloneqq k\langle \mathcal{D}^t \rangle/STU$ of the linear span of Jacobi diagrams by the STU-relation.

Horizontal weight systems

Definition

(linear span of horizontal chord diagrams modulo 2T/4T)

Let $k$ be a field (or just a commutative ring). Write

1. $\mathcal{D}^{pb}$ for the set of horizontal chord diagrams,

2. $k\langle \mathcal{D}^{pb}\rangle$ for its $k$-linear span,

3. $\mathcal{A}^{pb} \;\coloneqq\; k\langle \mathcal{D}^c\rangle/(2T,4T)$ for the quotient vector space by the 2T relations and horizontal 4T-relations.

(The superscript “${}^{pb}$”in Def. is for pure braids, alluding to the fact that horizontal weight systems are associated graded of Vassiliev braid invaraints.)

Definition

(horizontal weight system)

A $k$-valued horizontal weight system is a linear function on the linear span of horizontal chord diagrams modulo 2T&4T-relations (Def. )

$$w \;\colon\; \mathcal{A}^{pb} \longrightarrow k \,,$$

hence the $k$-vector space of horizontal weight systems is the dual vector space

$$\mathcal{W}_{pb} \;\coloneqq\; (\mathcal{A}^{pb})^\ast$$

Constructions of weight systems

Lie algebra weight systems

A large class of weight systems arises from reading a (horizontal) chord diagram as a string diagram in the evident way, and then labelling it by the structure morphisms of a Lie algebra object equipped with a Lie algebra representation internal to a suitable tensor category. This does yield weight systems because the required relations translate exactly to the structural equations satisfied by Lie modules (Jacobi identity and Lie action property).

The weight systems arising this way are called Lie algebra weight systems. See there for more.

Examples of weight systems which are not Lie algebra weight systems are rare. Originally it was conjectured that none exist (Bar-Natan 95, Conjecture 1, Bar-Natan & Stoimenow 97, Conjecture 2.4).

Eventually, a (counter-)example of a weight system which at least does not arise from any finite-dimensional super Lie algebra was given in Vogel 11.

Stringy weight systems

stringy weight systems

Rozansky-Witten weight systems

Rozansky-Witten weight systems

Properties

As the associated graded space of Vassiliev invariants

Proposition

(weight systems are associated graded of Vassiliev invariants)

For ground field $k = \mathbb{R}, \mathbb{C}$ the real numbers or complex numbers, there is for each natural number $n \in \mathbb{N}$ a canonical linear isomorphism

$$\mathcal{V}_n/\mathcal{V}_{n-1} \underoverset{\simeq}{\phantom{AAAA}}{\longrightarrow} \big( \mathcal{A}_n^u \big)^\ast$$

from

1. the quotient vector space of order-$n$ Vassiliev invariants of knots by those of order $n-1$

2. to the space of unframed weight systems of order $n$.

In other words, in characteristic zero, the graded vector space of unframed weight systems is the associated graded vector space of the filtered vector space of Vassiliev invariants.

(Bar-Natan 95, Theorem 1, following Kontsevich 93)

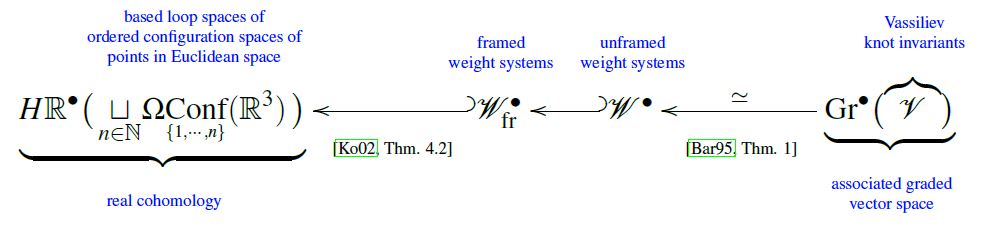
As cohomology of loop spaces of configuration spaces

weight systems are cohomology of loop space of configuration space:

For horizontal chord diagrams

Proposition

(integral horizontal weight systems are integral cohomology of based loop space of ordered configuration space of points in Euclidean space)

For ground ring $R = \mathbb{Z}$ the integers, there is, for each natural number $n$, a canonical isomorphism of graded abelian groups between

1. the integral weight systems

   $$\mathcal{W}_{pb} \;\coloneqq\; Hom_{\mathbb{Z} Mod} \big( \underset{ \mathcal{A}^{pb} }{ \underbrace{ \mathbb{Z} \langle \mathcal{D}^{pb} \rangle /(2T,4T) } } , \mathbb{Z} \big)$$

   on horizontal chord diagrams of $n$ strands (elements of the set $\mathcal{D}^{pb}$)

2. the integral cohomology of the based loop space of the ordered configuration space of n points in 3d Euclidean space:

$$H \mathbb{Z}^\bullet \big( \underset{n \in \mathbb{N}}{\sqcup} \Omega \underset{ {}^{\{1,\cdots,n\}} }{Conf} (\mathbb{R}^3) \big) \;\simeq\; (\mathcal{W}_{pb})^\bullet \;\simeq\; Gr^\bullet( \mathcal{V}_{pb}) \,.$$

(the second equivalence on the right is the fact that weight systems are associated graded of Vassiliev invariants).

This is stated as Kohno 02, Theorem 4.1

For round chord diagrams

Proposition

(weight systems are inside real cohomology of based loop space of ordered configuration space of points in Euclidean space)

For ground field $k = \mathbb{R}$ the real numbers, there is a canonical injection of the real vector space $\mathcal{W}$ of framed weight systems (here) into the real cohomology of the based loop spaces of the ordered configuration spaces of points in 3-dimensional Euclidean space:

$$\mathcal{W} \;\overset{\;\;\;\;}{\hookrightarrow}\; H\mathbb{R}^\bullet \Big( \underset{n \in \mathbb{N}}{\sqcup} \Omega \underset{{}^{\{1,\cdots,n\}}}{Conf} \big( \mathbb{R}^3 \big) \Big)$$

This is stated as Kohno 02, Theorem 4.2

Combining the above two propositions

1. weight systems are associated graded of Vassiliev invariants,

2. weight systems are cohomology of loop space of configuration space

we get this situation:

As cohomology of the knot graph complex

cohomology of knot graph complex is weight systems on chord diagrams

All horizontal weight systems are partitioned Lie algebra weight systems

• all horizontal weight systems are partitioned Lie algebra weight systems

Related concepts

chord diagrams	weight systems
linear chord diagrams, round chord diagrams Jacobi diagrams, Sullivan chord diagrams	Lie algebra weight systems, stringy weight system, Rozansky-Witten weight systems

knots	braids
chord diagram, Jacobi diagram	horizontal chord diagram
1T&4T relation	2T&4T relation/ infinitesimal braid relations
weight system	horizontal weight system
Vassiliev knot invariant	Vassiliev braid invariant
weight systems are associated graded of Vassiliev invariants	horizontal weight systems are cohomology of loop space of configuration space

• Kontsevich integral

References

General

Original articles:

• Dror Bar-Natan, On the Vassiliev knot invariants, Topology Volume 34, Issue 2, April 1995, Pages 423-472 (doi:10.1016/0040-9383(95)93237-2, pdf)

• Dror Bar-Natan, Vassiliev and Quantum Invariants of Braids, Geom. Topol. Monogr. 4 (2002) 143-160 (arxiv:q-alg/9607001)

Textbook accounts:

• Sergei Chmutov, Sergei Duzhin, Jacob Mostovoy, Section 4 of: Introduction to Vassiliev knot invariants, Cambridge University Press, 2012 (arxiv:1103.5628, doi:10.1017/CBO9781139107846)

• David Jackson, Iain Moffat, Section 11.7 of: An Introduction to Quantum and Vassiliev Knot Invariants, Springer 2019 (doi:10.1007/978-3-030-05213-3)

Lie algebra weight systems

Discussion of Lie algebra weight systems

From the construction given in Bar-Natan 95, Section 2.4 the interpretation of Lie algebra weight systems in terms of string diagrams for Lie algebra objects in tensor categories is evident, but standard textbooks in knot theory/combinatorics do not pick this up:

• Sergei Chmutov, Sergei Duzhin, Jacob Mostovoy, Chapter 6 of: Introduction to Vassiliev knot invariants, Cambridge University Press, 2012 (arxiv:1103.5628, doi:10.1017/CBO9781139107846)

• David Jackson, Iain Moffat, Section 14 of: An Introduction to Quantum and Vassiliev Knot Invariants, Springer 2019 (doi:10.1007/978-3-030-05213-3)

The interpretation of Lie algebra weight systems as string diagram-calculus and generalization to Lie algebra objects (motivated by generalization at least to super Lie algebras) is made more explicit in

• Arkady Vaintrob, Vassiliev knot invariants and Lie S-algebras, Mathematical Research Letters1, 579–595 (1994) (pdf)

• Pierre Vogel, Algebraic structures on modules of diagrams, Journal of Pure and Applied Algebra, Volume 215, Issue 6, June 2011, Pages 1292-1339 (doi:10.1016/j.jpaa.2010.08.013, pdf)

and fully explicit in

• Justin Roberts, Simon Willerton, Section 3 of: On the Rozansky-Witten weight systems, Algebr. Geom. Topol. 10 (2010) 1455-1519 (arXiv:math/0602653)

See also

• Vladimir Hinich, Arkady Vaintrob, Cyclic operads and algebra of chord diagrams, Sel. math., New ser. (2002) 8: 237 (arXiv:math/0005197)

• E. Kulakova, S. Lando, T. Mukhutdinova, G. Rybnikov, On a weight system conjecturally related to $\mathfrak{sl}_2$, European Journal of Combinatorics Volume 41, October 2014, Pages 266-277 (arXiv:1307.4933)

• Alexander Schrijver, On Lie algebra weight systems for 3-graphs (arXiv:1412.6923)

As the associated graded space of Vassiliev invariants

On spaces of weight systems as the associated graded spaces of Vassiliev invariants:

• Maxim Kontsevich, Vassiliev’s knot invariants, Advances in Soviet Mathematics, Volume 16, Part 2, 1993 (pdf)

• Dror Bar-Natan, On the Vassiliev knot invariants, Topology Volume 34, Issue 2, April 1995, Pages 423-472 (doi:10.1016/0040-9383(95)93237-2, pdf)

As cohomology of loop spaces of configuration spaces

On weight systems as the real cohomology of based loop spaces of ordered configuration spaces of points:

• Toshitake Kohno, Vassiliev invariants and de Rham complex on the space of knots,

  In: Yoshiaki Maeda, Hideki Omori and Alan Weinstein (eds.), Symplectic Geometry and Quantization, Contemporary Mathematics 179 (1994): 123-123 (doi:10.1090/conm/179)

• Fred Cohen, Samuel Gitler, Loop spaces of configuration spaces, braid-like groups, and knots, In: Jaume Aguadé, Carles Broto, Carles Casacuberta (eds.) Cohomological Methods in Homotopy Theory. Progress in Mathematics, vol 196. Birkhäuser, Basel 2001 (doi:10.1007/978-3-0348-8312-2_7)

• Toshitake Kohno, Loop spaces of configuration spaces and finite type invariants, Geom. Topol. Monogr. 4 (2002) 143-160 (arXiv:math/0211056)

• Fred Cohen, Samuel Gitler, On loop spaces of configuration spaces, Trans. Amer. Math. Soc. 354 (2002), no. 5, 1705–1748, (jstor:2693715, MR2002m:55020)

Chord diagrams and weight systems in Physics

The following is a list of references that involve (weight systems on) chord diagrams/Jacobi diagrams in physics:

1. In Chern-Simons theory

2. In Dp-D(p+2) brane intersections

3. In quantum many body models for for holographic brane/bulk correspondence:

   1. In AdS2/CFT1, JT-gravity/SYK-model

   2. As dimer/bit thread codes for holographic entanglement entropy

For a unifying perspective (via Hypothesis H) and further pointers, see:

• Hisham Sati, Urs Schreiber, Differential Cohomotopy implies intersecting brane observables, Adv. Theor. Math. Phys. 26 4 (2022) [doi:10.4310/ATMP.2022.v26.n4.a4arXiv:1912.10425]

• David Corfield, Hisham Sati, Urs Schreiber: Fundamental weight systems are quantum states Lett. Math. Phys. 113 112 (2023) [arXiv:2105.02871, doi:10.1007/s11005-023-01725-4]

• Carlo Collari, A note on weight systems which are quantum states, Can. Math. Bull. 66 4 (2023) [doi:10.4153/S0008439523000206, arXiv:2210.05399]

Review:

• Carlo Collari, Weight systems which are quantum states, talk at QFT and Cobordism, CQTS (Mar 2023) $[$web, pdf$]$

In Chern-Simons theory

Since weight systems are the associated graded of Vassiliev invariants, and since Vassiliev invariants are knot invariants arising as certain correlators/Feynman amplitudes of Chern-Simons theory in the presence of Wilson lines, there is a close relation between weight systems and quantum Chern-Simons theory.

Historically this is the original application of chord diagrams/Jacobi diagrams and their weight systems, see also at graph complex and Kontsevich integral.

from Bar-Natan 1991

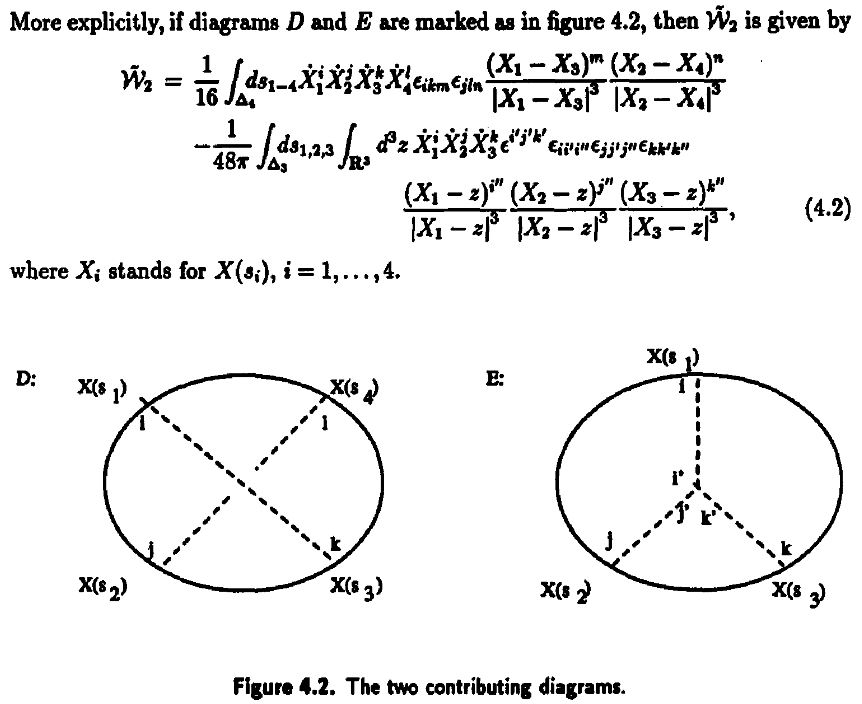
• Dror Bar-Natan, Perturbative aspects of the Chern-Simons topological quantum field theory, thesis 1991 (spire:323500, proquest:303979053, BarNatanPerturbativeCS91.pdf)

• Maxim Kontsevich, Vassiliev’s knot invariants, Advances in Soviet Mathematics, Volume 16, Part 2, 1993 (pdf)

• Daniel Altschuler, Laurent Freidel, Vassiliev knot invariants and Chern-Simons perturbation theory to all orders, Commun. Math. Phys. 187 (1997) 261-287 (arxiv:q-alg/9603010)

• Alberto Cattaneo, Paolo Cotta-Ramusino, Riccardo Longoni, Configuration spaces and Vassiliev classes in any dimension, Algebr. Geom. Topol. 2 (2002) 949-1000 (arXiv:math/9910139)

• Alberto Cattaneo, Paolo Cotta-Ramusino, Riccardo Longoni, Algebraic structures on graph cohomology, Journal of Knot Theory and Its Ramifications, Vol. 14, No. 5 (2005) 627-640 (arXiv:math/0307218)

Reviewed in:

• Ismar Volić, Section 4 of: Configuration space integrals and the topology of knot and link spaces, Morfismos, Vol 17, no 2, 2013 (arxiv:1310.7224)

Applied to Gopakumar-Vafa duality:

• Dave Auckly, Sergiy Koshkin, Introduction to the Gopakumar-Vafa Large $N$ Duality, Geom. Topol. Monogr. 8 (2006) 195-456 (arXiv:0701568)

See also

• Marcos Mariño, Chern-Simons theory, matrix integrals, and perturbative three-manifold invariants, Commun. Math. Phys. 253 (2004) 25-49 (arXiv:hep-th/0207096)

• Stavros Garoufalidis, Marcos Mariño, On Chern-Simons matrix models (pdf, pdf)

For single trace operators in AdS/CFT duality

Interpretation of Lie algebra weight systems on chord diagrams as certain single trace operators, in particular in application to black hole thermodynamics

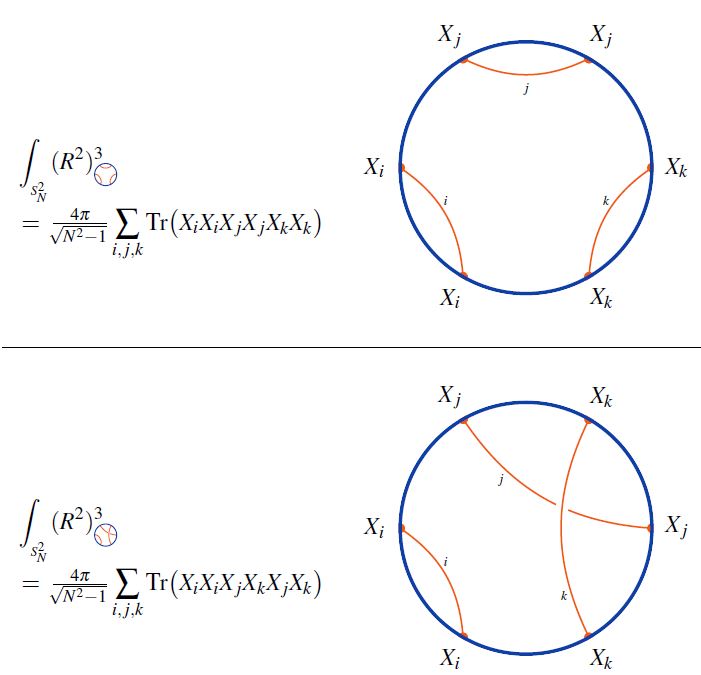
• Micha Berkooz, Prithvi Narayan, Joan Simón, Section 2.1 of Chord diagrams, exact correlators in spin glasses and black hole bulk reconstruction, JHEP 08 (2018) 192 (arxiv:1806.04380)

In $AdS_2/CFT_1$, JT-gravity/SYK-model

Discussion of (Lie algebra-)weight systems on chord diagrams as SYK model single trace operators:

• Antonio M. García-García, Yiyang Jia, Jacobus J. M. Verbaarschot, Exact moments of the Sachdev-Ye-Kitaev model up to order $1/N^2$, JHEP 04 (2018) 146 (arXiv:1801.02696)

• Yiyang Jia, Jacobus J. M. Verbaarschot, Section 4 of: Large $N$ expansion of the moments and free energy of Sachdev-Ye-Kitaev model, and the enumeration of intersection graphs, JHEP 11 (2018) 031 (arXiv:1806.03271)

• Micha Berkooz, Prithvi Narayan, Joan Simón, Chord diagrams, exact correlators in spin glasses and black hole bulk reconstruction, JHEP 08 (2018) 192 (arxiv:1806.04380)

following:

• László Erdős, Dominik Schröder, Phase Transition in the Density of States of Quantum Spin Glasses, D. Math Phys Anal Geom (2014) 17: 9164 (arXiv:1407.1552)

which in turn follows

• Philippe Flajolet, Marc Noy, Analytic Combinatorics of Chord Diagrams, pages 191–201 in Daniel Krob, Alexander A. Mikhalev,and Alexander V. Mikhalev, (eds.), Formal Power Series and Algebraic Combinatorics, Springer 2000 (doi:10.1007/978-3-662-04166-6_17)

from Narovlansky 2019

With emphasis on the holographic content:

• Micha Berkooz, Mikhail Isachenkov, Vladimir Narovlansky, Genis Torrents, Section 5 of: Towards a full solution of the large $N$ double-scaled SYK model, JHEP 03 (2019) 079 (arxiv:1811.02584)

• Vladimir Narovlansky, Slide 23 (of 28) of: Towards a Solution of Large $N$ Double-Scaled SYK, 2019 (pdf)

• Micha Berkooz, Mikhail Isachenkov, Prithvi Narayan, Vladimir Narovlansky, Quantum groups, non-commutative $AdS_2$, and chords in the double-scaled SYK model [arXiv:2212.13668]

• Herman Verlinde, Double-scaled SYK, Chords and de Sitter Gravity [arXiv:2402.00635]

• Micha Berkooz, Nadav Brukner, Yiyang Jia, Ohad Mamroud, A Path Integral for Chord Diagrams and Chaotic-Integrable Transitions in Double Scaled SYK [arXiv:2403.05980]

and specifically in relation, under AdS2/CFT1, to Jackiw-Teitelboim gravity:

• Andreas Blommaert, Thomas Mertens, Henri Verschelde, The Schwarzian Theory - A Wilson Line Perspective, JHEP 1812 (2018) 022 (arXiv:1806.07765)

• Andreas Blommaert, Thomas Mertens, Henri Verschelde, Fine Structure of Jackiw-Teitelboim Quantum Gravity, JHEP 1909 (2019) 066 (arXiv:1812.00918)

• Henry W. Lin, The bulk Hilbert space of double scaled SYK, J. High Energ. Phys. 2022 60 (2022) $[$arXiv:2208.07032, doi:10.1007/JHEP11(2022)060$]$

• Henry W. Lin, Douglas Stanford, A symmetry algebra in double-scaled SYK $[$arXiv:2307.15725$]$

• Micha Berkooz, Ohad Mamroud: A Cordial Introduction to Double Scaled SYK [arXiv:2407.09396]

• Adel A. Rahman, Leonard Susskind: $p$-Chords, Wee-Chords, and de Sitter Space [arXiv:2407.12988]

In D$p$/D$(p+2)$-brane intersections

from Sati and Schreiber 19c

Discussion of weight systems on chord diagrams as single trace observables for the non-abelian DBI action on the fuzzy funnel/fuzzy sphere non-commutative geometry of Dp-D(p+2)-brane intersections (hence Yang-Mills monopoles):

• Sanyaje Ramgoolam, Bill Spence, S. Thomas, Section 3.2 of: Resolving brane collapse with $1/N$ corrections in non-Abelian DBI, Nucl. Phys. B703 (2004) 236-276 (arxiv:hep-th/0405256)

• Simon McNamara, Constantinos Papageorgakis, Sanyaje Ramgoolam, Bill Spence, Appendix A of: Finite $N$ effects on the collapse of fuzzy spheres, JHEP 0605:060, 2006 (arxiv:hep-th/0512145)

• Simon McNamara, Section 4 of: Twistor Inspired Methods in Perturbative FieldTheory and Fuzzy Funnels, 2006 (spire:1351861, pdf, pdf)

• Constantinos Papageorgakis, p. 161-162 of: On matrix D-brane dynamics and fuzzy spheres, 2006 (pdf)

As codes for holographic entanglement entropy

From Yan 20

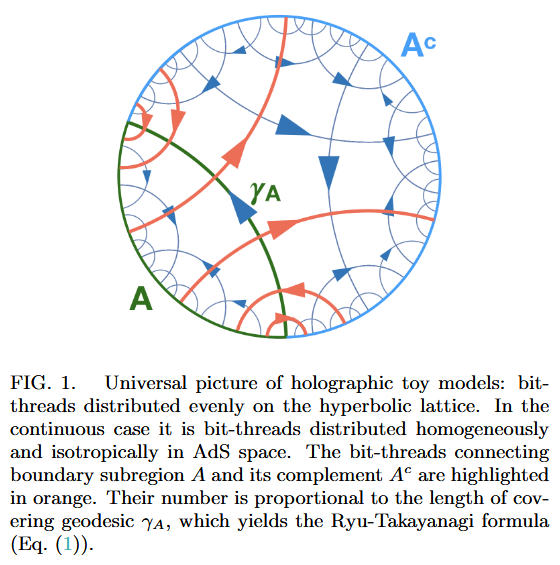
Chord diagrams encoding Majorana dimer codes and other quantum error correcting codes via tensor networks exhibiting holographic entanglement entropy:

• Alexander Jahn, Marek Gluza, Fernando Pastawski, Jens Eisert, Majorana dimers and holographic quantum error-correcting code, Phys. Rev. Research 1, 033079 (2019) (arXiv:1905.03268)

• Han Yan, Geodesic string condensation from symmetric tensor gauge theory: a unifying framework of holographic toy models, Phys. Rev. B 102, 161119 (2020) (arXiv:1911.01007)

From Jahn and Eisert 21

For Dyson-Schwinger equations

Discussion of round chord diagrams organizing Dyson-Schwinger equations:

• Nicolas Marie, Karen Yeats, A chord diagram expansion coming from some Dyson-Schwinger equations, Communications in Number Theory and Physics, 7(2):251291, 2013 (arXiv:1210.5457)

• Markus Hihn, Karen Yeats, Generalized chord diagram expansions of Dyson-Schwinger equations, Ann. Inst. Henri Poincar Comb. Phys. Interact. 6 no 4:573-605 (arXiv:1602.02550)

• Paul-Hermann Balduf, Amelia Cantwell, Kurusch Ebrahimi-Fard, Lukas Nabergall, Nicholas Olson-Harris, Karen Yeats, Tubings, chord diagrams, and Dyson-Schwinger equations [arXiv:2302.02019]

Review in:

• Ali Assem Mahmoud, Section 3 of: On the Enumerative Structures in Quantum Field Theory (arXiv:2008.11661)

Other

Appearance of horizontal chord diagrams in discussion of neutrino interactions in supernovae:

• Duff Neill, Hanqing Liu, Joshua Martin, Alessandro Roggero: Scattering Neutrinos, Spin Models, and Permutations [arXiv:2406.18677]