nLab Jacobi identity
This entry is about the identity in Lie theory. For another identity named after Carl Jacobi, see at Jacobi theta-function and Jacobi form.
Context
Lie theory
∞-Lie theory (higher geometry)
Background
Smooth structure
Higher groupoids
Lie theory
∞-Lie groupoids
∞-Lie algebroids
Formal Lie groupoids
Cohomology
Homotopy
Related topics
Examples
-Lie groupoids
-Lie groups
-Lie algebroids
-Lie algebras
Contents
Idea
The Jacobi identity is an important equational identity that holds in Lie algebras and is also of interest in other algebras. It can be generalised to higher algebras.
There is a non-additive non-abelian form of the Jacobi identity that occurs in considering certain examples in identities among relations in the presentation of certain groups. There it is also called the Hall-Witt identity.
For -algebras
Definition
Given a nonassociative algebra over a field or a ring , whose bilinear product is denoted by bracket , the Jacobi identity holds for a triple of elements if
The principal example is that of a Lie algebra: here the Jacobi identity by definition holds for all triples of elements (and the bracket is skew-symmetric).
Relation to the Leibniz identity
If the bracket is skew-symmetric the Jacobi identity for all triples is equivalent to the Leibniz identity that for all , the linear map is a derivation with respect to the Lie bracket:
One can also consider right derivations (right Leibniz identity), what is again equivalent in the presence of antisymmetry:
Left and right Leibniz algebras generalize Lie algebras by having a left or right Leibniz identity, but not necessarily antisymmetry of the bracket. In particular, Jacobi identity, and left and right Leibniz identities do not need to coincide without antisymmetry.
In terms of Chevalley–Eilenberg algebras
A useful way to think of Jacobi identity for finite-dimensional Lie algebras, is dually in terms of the Chevalley-Eilenberg algebra of the Lie algebra (see there for details). In terms of this dg-algebra , the Lie bracket is encoded in the differential
and the Jacobi identity is equivalent to the statement that this differential squares to
In terms of string diagrams / Jacobi diagrams
In string diagram-notation for Lie algebra objects interal to tensor categories, the Lie action property looks as follows:
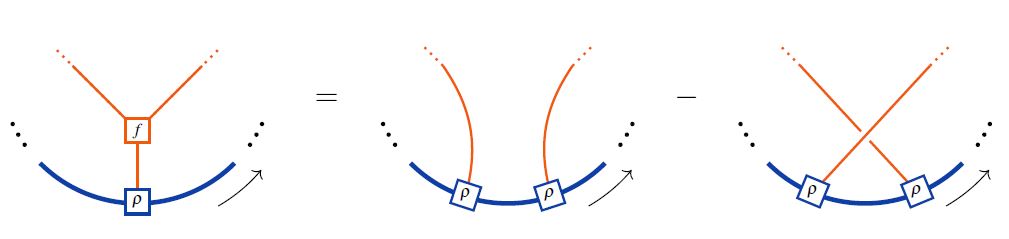
where the last line shows the equivalence to the Jacobi identity on the Lie algebra object itself in the case that the Lie action is the adjoint action.
graphics from Sati-Schreiber 19c
In the language of Jacobi diagrams this is called the STU-relation. and is the reason behind the existence of Lie algebra weight systems in knot theory.
For -algebras
When Lie algebras are generalized to ∞-Lie algebras, the Jacobi identity in terms of the binary bracket is relaxed to hold only up to a natural isomorphism called the jacobiator, ,
where is the differential.
graphics from Sati-Schreiber 19c On the other hand, in terms of the Chevalley-Eilenberg algebra this is still encoded in just (see there for details).
Related entries
Last revised on April 28, 2021 at 15:45:31. See the history of this page for a list of all contributions to it.