nLab Toda bracket

Contents

Context

Homotopy theory

Algebraic topology

Idea
Preliminaries
Definitions
Applications
Related concepts
References

the stable homotopy groups of spheres are not really understood until the Toda bracket structure is revealed (Iaksen-Wang-Xu 20, p. 17)

Idea

Given a pointed (∞,1)-category $\mathcal{C}$ (such as that presented by the classical model structure on pointed topological spaces) or at least a (2,1)-category (such as its homotopy 2-category), the Toda bracket (Toda 62) is the operation that takes a sequence of 3 composable 1-morphisms in $\mathcal{C}$

X_0 \overset{\;\;f_1\;\;}{\longrightarrow} X_1 \overset{\;\;f_2\;\;}{\longrightarrow} X_2 \overset{\;\;f_3\;\;}{\longrightarrow} X_3 \,,

equipped with a pair of overlapping null homotopies

to the higher homotopy-equivalence class of their pasting-composite, which is a 2-morphism loop (on the zero 1-morphism) in the (∞,1)-categorical hom space $\mathcal{C}(X_0,X_3) \in$ ∞Groupoids, hence an element in its fundamental group $\pi_1 \mathcal{C}(X_0,X_3)$ :

Or rather, the Toda bracket is usually and equivalently taken to be the homotopy class of the 1-morphism $\vdash \big( (\phi_2 \cdot f_1) \circ (f_3 \cdot \phi_1) \big)$ that classifies this homotopy, via the universal property of homotopy fibers/homotopy cofibers:

if $\mathcal{C}$ admits finite (∞,1)-colimits or at least reduced suspensions $\Sigma(-)$ (homotopy cofibers of zero morphisms), so that this 2-morphism between zero morphisms corresponds to a 1-morphism of the form:

$\Sigma X_0 \overset{ \vdash (\phi_2 \cdot f_1) \circ (f_3 \cdot \phi_1) } {\longrightarrow} X_3$
if $\mathcal{C}$ admits finite (∞,1)-limits or at least based loop space objects $\Omega(-)$ (homotopy fibers of zero morphisms), so that this 2-morphism between zero morphisms corresponds to a 1-morphism of the form

$X_0 \overset{ \vdash (\phi_2 \cdot f_1) \circ (f_3 \cdot \phi_1) } {\longrightarrow} \Omega X_3 \,,$

or both, as we shall assume for ease of notation, then the Toda bracket is the homotopy class of this 1-morphism in the homotopy category:

(1)

\array{ \big\langle f_1, f_2, f_3 \big\rangle_{(\phi_1,\phi_2)} \;\coloneqq\; \big[ \vdash (\phi_2 \cdot f_1) \circ (f_3 \cdot \phi_1) \big] \; \in && \pi_0 \mathcal{C} \big( \Sigma X_0, X_3 \big) \\ & \;\simeq\; & \pi_0 \mathcal{C} \big( X_0, \Omega X_3 \big) \\ & \; \simeq \; & \pi_1 \mathcal{C} \big( X_0, X_3 \big) } \,.

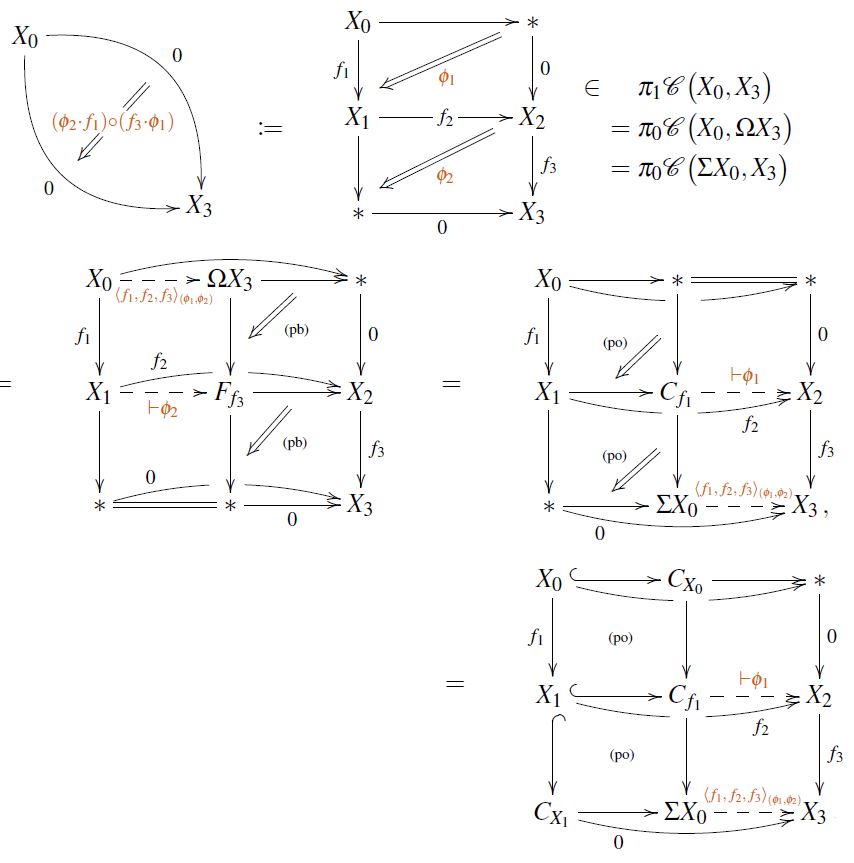
Here the last pasting diagram on the bottom right shows the homotopy cofiber-construction equivalently realized via mapping cones (ordinary cofiber coproducts after resolving points to cones), by which one may present the top homotopy coherent diagram in, for instance, any pointed cofibration category- or model category-presentation of the pointed (∞,1)-category $\mathcal{C}$ .

It is in this last form, by “consecutively extending maps over cones”, that the Toda bracket was introduced in Toda 62, and in which it is still presented in most references to date.

The more abstract formulation shown at the top, via homotopy-pasting diagrams, is made more explicit in Hardie-Kamps-Kieboom 99, (0.2)-(0.3), Hardie-Marcum-Oda 01, Hardie-Kamps-Marcum 02, (2.2) (formalized there inside a homotopy 2-category).

From this abstract homotopy-pasting perspective it is manifest that the set of choices of refined Toda brackets (1) for given maps $(f_1, f_2, f_2)$ is, if inhabited, a torsor over the direct product group

(2)

\begin{aligned} G_{(X_0, X_1, X_2, X_3)} & \coloneqq \; \pi_1 \mathcal{C}(X_0,X_2) \times \pi_1 \mathcal{C}(X_1, X_3)^{op} \\ & = \; \pi_0 \mathcal{C}(X_0, \Omega X_2) \times \pi_0 \mathcal{C}(X_1, \Omega X_3)^{op} \\ & = \; \pi_0 \mathcal{C}(\Sigma X_0, X_2) \times \pi_0 \mathcal{C}(\Sigma X_1, X_3)^{op} \,, \end{aligned}

whose action is given by the evident composition of 2-morphisms:

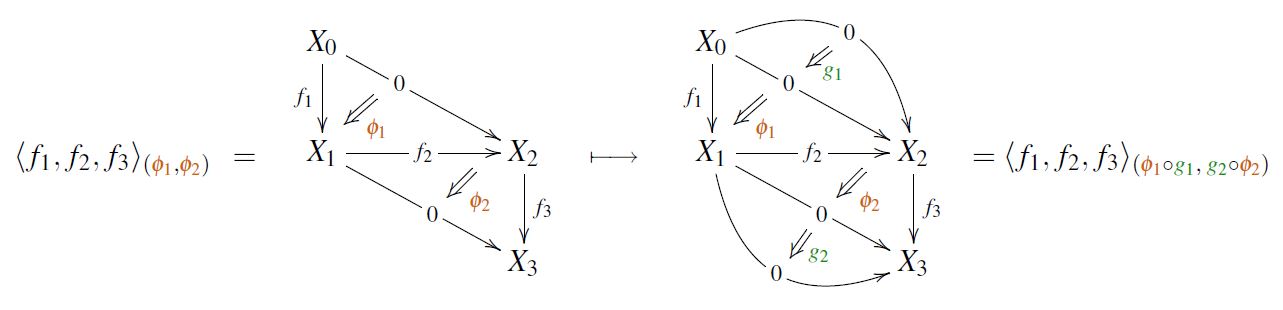
The plain Toda bracket is meant to be independent of the choice of null homotopies $(\phi_1,\phi_2)$ and thus taken to be the image of (1) in the quotient set by this action

\big\langle f_1, f_2, f_3 \big\rangle \;\; \in \;\; Ho(\mathcal{C}) \big( X_0, \Omega X_3 \big) \big/ G_{X_0, X_1, X_2, X_3} \,.

With elements in the quotient set identified with the orbit-sets, the plain Toda bracket may be taken to be the orbit of this action, hence the subset

(3)

\array{ \big\langle f_1, f_2, f_3 \big\rangle \;\coloneqq\; \left\{ \big\langle f_1, f_2, f_3 \big\rangle_{(\phi_1,\phi_2)} \; \left\vert \; \array{ 0 &\overset{\phi_1}{\Rightarrow}& f_2 \circ f_1 \\ f_3 \circ f_2 &\underset{\phi_2}{\Rightarrow}& 0 } \right. \right\} \; \subset && \pi_0 \mathcal{C} \big( \Sigma X_0, X_3 \big) \\ & \;\simeq\; & \pi_0 \mathcal{C} \big( X_0, \Omega X_3 \big) \\ & \; \simeq \; & \pi_1 \mathcal{C} \big( X_0, X_3 \big) }

of all the classes (1) as one varies the null homotopies $(\phi_1,\phi_2)$ .

This means that the plain Toda bracket (3) is not a function with values, but a bundle with fibers (whose elements are the refined Toda brackets (1)):

In any case, the Toda bracket may be thought of as being in homotopy theory what the Massey product is in cohomology theory: It is a “secondary invariant”, which exists (has inhabited fibers) when/since “primary invariants” – namely the homotopy classes of the morphisms $f_2 \circ f_1$ and $f_3\circ f_2$ – vanish, as witnessed by the null homotopies.

A generalization of the Toda bracket produces an invariant for sequences of morphisms, equipped with consecutive pair-wise null-homotopies, which may contain possibly more than three morphisms; this higher Toda bracket was maybe first considered in Cohen 68, Sec. 2

Preliminaries

Consider a sequence of maps $A_0 \to A_1 \to A_2 \to A_3$ . If the composites $A_0 \to A_2$ and $A_1\to A_3$ are nulhomotopic, then one has a diagram

\begin{array}{ccccc} A_0 & \to & A_1 & \to & * \\ \downarrow & & \downarrow & & \downarrow \\ * & \to & A_2 & \to & A_3 \end{array}

any choice of homotopies in the two squares gives a map $\Sigma A_0 \to A_3$ .

Define $C$ and $D$ to be the cofibers of $A_0 \to A_1$ and $A_1\to A_2$ , respectively. A choice of homotopy $A_0 \to A_2 \sim 0$ corresponds to a choice of factorization $A_1 \to C \to A_2$ , which gives a diagram of pushout squares

\begin{array}{ccccccc} A_0 & \to & A_1 & \to & * \\ \downarrow & & \downarrow & & \downarrow \\ * & \to & C &\to & \Sigma A_0 & \to & *\\ & & \downarrow & & \downarrow & & \downarrow \\ & & A_2 & \to & D & \to & C' \end{array}

It is to be noted that the map $\Sigma A_0 \to D$ and possibly the object $C'$ depend on the choice of factor $C \to A_2$ , but that $A_2 \to D$ does not, in any meaningful sense, so depend: this is just the structure map of the cofiber of $A_1\to A_2$ . Note that the cofiber $C'$ of $C\to A_2$ is thus equivalent to that of $\Sigma A_0 \to D$ ; but again the role of choices must be studied.

Definitions

A sequence of maps $A_0 \to A_1 \to \cdots \to A_n$ will be called a bracket sequence (a novel phrase for the purposes of this entry) in either of two cases:

$n = 3$ and the composites $A_0 \to A_2$ and $A_1 \to A_3$ are nulhomotopic; OR
$n \gt 3$ , and (using the preceding notations), there are choices of factor $C\to A_2$ and $D \to A_3$ such that the induced sequence $\Sigma A_0 \to D \to A_3 \to \cdots \to A_n$ is a bracket sequence.

In all cases, a bracket sequence leads to a three-map sequence

\Sigma^m A_0 \to D_m \to A_{m+2} \to A_{m+3}

in which consecutive maps compose trivially, and so there are induced choices of maps

\Sigma^{m+1} A_0 \to A_{m+3} .

The collection of all such maps, taking all compatible variations, is the Toda Bracket of the bracket sequence.

Among the bracket sequences, a particular family arises which here will be called null-bracket (again, a novel phrase). A sequence will be called null-bracket if

$n=2$ and $A_0 \to A_2$ is trivial, OR
$n \gt 2$ , and there is a choice of factorization $A_1 \to C \to A_2$ such that the sequence $C \to A_2 \to \cdots \to A_n$ is null-bracket.

If the Toda bracket for a bracket sequence includes the trivial map $\Sigma^{m+1} A_0 \to A_{m+3}$ then the sequence is null-bracket.

Applications

By definition, if a sequence is a bracket sequence AND NOT a null-bracket sequence, it follows that all the relevant maps $\Sigma^{k} A_0 \to A_n$ are nontrivial. Things like these Toda brackets have been studied by many (FIXME: references later) and especially the length-three brackets used by H. Toda to describe most of $\pi_k \mathbb{S}^n$ for $k \lt 31$ or so.

In (Cohen, 1968) is given a criterion for stable maps of spheres to inhabit non-null Toda brackets; this turns out to be most of the stable homotopy groups of spheres $\pi_* \mathbb{S}$ , and furthermore the maps in the bracket sequences can be chosen from a very small set (_FIXME_: be more precise! degree maps $n \iota$ , Hopf maps $\eta, \theta,\sigma$ , and $\alpha_p$ … )

Related concepts

References

The concept of Toda brackets is due to:

Hirosi Toda, Composition Methods in Homotopy Groups of Spheres, Annals of Mathematics Studies Volume 49, Princeton University Press (1962) (jstor:j.ctt1bgzb5t)

and the concept of higher Toda brackets appears around

Joel Cohen, Section 2 of: The decomposition of stable homotopy, Annals of Mathematics (2) 87 (2): 305–320 (1968) (doi:10.2307/1970586)

The conceptualization of Toda brackets a homotopy coherent pasting diagrams in a pointed homotopy 2-category (regarded as a strict (2,1)-category) is made explicit in:

Keith Hardie, Klaus Heiner Kamps, Rudger Kieboom, Higher homotopy groupoids and Toda brackets, Homology Homotopy Appl. Volume 1, Number 1 (1999), 117-134 (euclid:hha/1139840198)
Keith Hardie, Howard Marcum, Nobuyuki Oda, Bracket operations in the homotopy theory of a 2-category, Rend. Ist. Mat. Univ. Trieste 33, 19–70 (2001) (rendiconti:33/02)
Keith Hardie, Klaus Heiner Kamps, Howard Marcum, The Toda bracket in the homotopy category of a track bicategory, Journal of Pure and Applied Algebra Volume 175, Issues 1–3, 8 November 2002, Pages 109-133 (doi:10.1016/S0022-4049(02)00131-7)
Howard Marcum, Nobuyuki Oda, Long Box Bracket Operations in Homotopy Theory, Appl Categor Struct 19, 137–173 (doi:10.1007/s10485-009-9186-3)

Application of Toda brackets to the concrete computations of stable homotopy groups of spheres:

Toda 62
Hardie-Marcum-Oda 01, Sec. 7
Daniel Isaksen, Guozhen Wang, Zhouli Xu, More stable stems (arXiv:2001.04511)