nLab fundamental group of the circle is the integers
Context
Homotopy theory
homotopy theory, (∞,1)-category theory, homotopy type theory
flavors: stable, equivariant, rational, p-adic, proper, geometric, cohesive, directed…
models: topological, simplicial, localic, …
see also algebraic topology
Introductions
Definitions
Paths and cylinders
Homotopy groups
Basic facts
Theorems
Contents
Statement
A basic statement in homotopy theory:
Proposition
(fundamental group of the circle is the integers)
The fundamental group of the circle is the additive group of integers:
and the isomorphism is given by assigning winding number.
Here in the context of topological homotopy theory the circle is the topological subspace of the Euclidean plane with its metric topology, or any topological space of the same homotopy type. More generally, the circle in question is, as a homotopy type, the homotopy pushout
hence the homotopy type with the universal property that it makes a homotopy commuting diagram of the form
Proofs
In topological point-set homotopy theory
We discuss the classical proof in point-set topological homotopy theory.
Proof
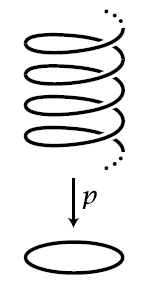
The universal covering space of is the real line (by this example):
Since the circle is locally path-connected (this example) and semi-locally simply connected (this example) the fundamental theorem of covering spaces applies and gives that the automorphism group of over equals the automorphism group of its monodromy permutation representation:
Moreover, as a corollary of the fundamental theorem of covering spaces we have that the monodromy representation of a universal covering space is given by the action of the fundamental group on itself (this prop.).
But the automorphism group of any group regarded as an action on itself by left multiplication is canonically isomorphic to that group itself (by this example), hence we have
Therefore to conclude the proof it is now sufficient to show that
# To that end, consider a homeomorphism of the form
Let be any point, and consider the restriction of to the fibers over the complement:
By the covering space property we have (via this example) a homeomorphism
Therefore, up to homeomorphism, the restricted function is of the form
By the universal property of the product topological space this means that is equivalently given by its two components
By the commutativity of the above diagram, the first component is fixed to be . Moreover, by the fact that is a discrete space it follows that the second component is a locally constant function (by this example). Therefore, since the product space with a discrete space is a disjoint union space (via this example)
and since the disjoint summands are connected topological spaces (this example), it follows that the second component is a constant function on each of these summands (by this example).
Finally, since every function out of a discrete topological space is continuous, it follows in conclusion that the restriction of to the fibers over is entirely encoded in an endofunction of the set of integers
by
Now let be another point, distinct from . The same analysis as above applies now to the restriction of to and yields a function
Since
is an open cover of , it follows that is uniquely fixed by its restrictions to these two subsets.
Now unwinding the definition of shows that the condition that the two restrictions coincide on the intersection implies that there is such that and .
This shows that .
In homotopy type theory
There is also a purely synthetic a proof in homotopy type theory (Licata-Shulman 13, UF, corollary 8.1.10).
Consequences
Example
(isomorphism classes of coverings of the circle are conjugacy classes in the symmetric group)
The monodromy construction assigns to an isomorphism class of covering spaces over the circle with fibers consisting of elements conjugacy classes of elements the symmetric group :
To see this, we may without restriction (via this prop.) choose a basepoint so that a monodromy representation is equivalently a groupoid morphism of the form
Since is the free abelian group on a single generator, such as morphism is uniquely determined by the image of . This is taken to some isomorphism of the set . If we choose any identification , then this defines an element in the symmetric group:
Now if
is an isomorphism of covering spaces, then by the fundamental theorem of covering spaces this corresponds bijectively to a homomorphism of representations
which in turn is by definition a homotopy (natural isomorphism) between the monodromy functors .
The combination of the naturality square of this natural isomorphism with the above identification yields the following diagram
The commutativity of the total rectangle says that the permutations and are related by conjugation with the element .
Example
(three-sheeted covers of the circle)
Consider the three-sheeted covering spaces of the circle.
By example these are, up to isomorphism, given by the conjugacy classes of the elements of the symmetric group on three elements. These in turn are labeled by the cycle structure of the elements (this prop.).
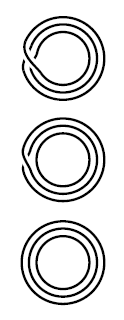
For the symmetric group on three elements there are three such classes
The corresponding covering spaces of the circle are shown in the graphics.
graphics grabbed from Hatcher
References
In topological homotopy theory
Lecture notes on the classical discussion include
-
Friedhelm Waldhausen, p. 63-77 of Topologie (pdf)
-
Jesper Møller, theorem 3.1 in The fundamental group and covering spaces (2011) (pdf)
In homotopy type theory
The proof in homotopy type theory is discussed in
-
Daniel Licata, Michael Shulman, Calculating the Fundamental Group of the Circle in Homotopy Type Theory, (arXiv:1301.3443)
-
Univalent Foundations Project, section 8.1 of Homotopy Type Theory – Univalent Foundations of Mathematics
the HoTT-Rocq-code is at
- The HoTT Coq-HoTT library: Pi1S1.v
Last revised on July 7, 2025 at 23:02:14. See the history of this page for a list of all contributions to it.