nLab Wick algebra -- table

	free field algebra of quantum observables	physics terminology	maths terminology
1)	supercommutative product	$\phantom{AA} :A_1 A_2:$ normal ordered product	$\phantom{AA} A_1 \cdot A_2$ pointwise product of functionals
2)	non-commutative product (deformation induced by Poisson bracket)	$\phantom{AA} A_1 A_2$ operator product	$\phantom{AA} A_1 \star_H A_2$ star product for Wightman propagator
3)		$\phantom{AA} T(A_1 A_2)$ time-ordered product	$\phantom{AA} A_1 \star_F A_2$ star product for Feynman propagator
	perturbative expansion of 2) via 1)	Wick's lemma	Moyal product for Wightman propagator $\Delta_H$ $\begin{aligned} & A_1 \star_H A_2 = \\ & ((-)\cdot (-)) \circ \exp \left( \hbar \int (\Delta_H)^{ab}(x,y) \frac{\delta}{\delta \mathbf{\Phi}^a(x)} \otimes \frac{\delta}{\delta \mathbf{\Phi}^b(y)} \right)(A_1 \otimes A_2) \end{aligned}$
	perturbative expansion of 3) via 1)	Feynman diagrams	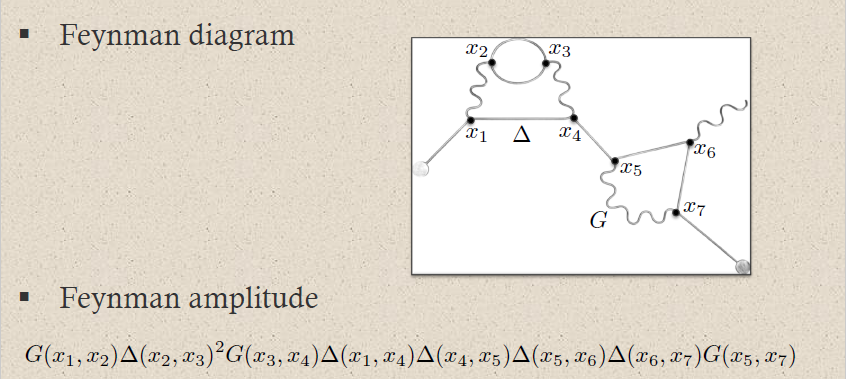Moyal product for Feynman propagator $\Delta_F$ $\begin{aligned} & A_1 \star_F A_2 = \\ & ((-)\cdot (-)) \circ \exp \left( \hbar \int (\Delta_F)^{ab}(x,y) \frac{\delta}{\delta \mathbf{\Phi}^a(x)} \otimes \frac{\delta}{\delta \mathbf{\Phi}^b(y)} \right)(A_1 \otimes A_2) \end{aligned}$