nLab Wick's lemma
Context
Measure and probability theory
Measure theory
Probability theory
Information geometry
Thermodynamics
Theorems
Applications
Physics
physics, mathematical physics, philosophy of physics
Surveys, textbooks and lecture notes
theory (physics), model (physics)
experiment, measurement, computable physics
-
-
-
Axiomatizations
-
Tools
-
Structural phenomena
-
Types of quantum field thories
-
Contents
Idea
Wick’s lemma is a combinatorial formula for the product in associative algebras that appear in the context of free field theory.
From the point of view of path integral quantization, Wick’s lemma is about the moments of Gaussian probability distributions. See at Feynman diagram for more on this.
From the point of view of causal perturbation theory Wick’s lemma expresses the Moyal deformation quantization of a free field theory (Wick algebras) in terms of operator products on.
| free field algebra of quantum observables | physics terminology | maths terminology | |
|---|---|---|---|
| 1) | supercommutative product | normal ordered product | pointwise product of functionals |
| 2) | non-commutative product (deformation induced by Poisson bracket) | operator product | star product for Wightman propagator |
| 3) | time-ordered product | star product for Feynman propagator | |
| perturbative expansion of 2) via 1) | Wick's lemma  | Moyal product for Wightman propagator | |
| perturbative expansion of 3) via 1) | Feynman diagrams 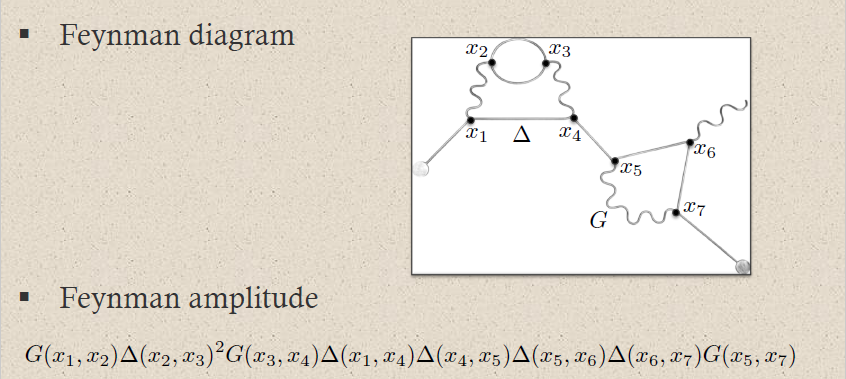 | Moyal product for Feynman propagator |
From the point of view of BV-quantization Wick’s lemma arises as a consequence of the homological perturbation lemma (Gwilliam, section 2.3).
Statement
Let be the Wick algebra of the free scalar field, hence the space of microcausal observables with product the star product induced by the Wightman propagator:
Then the evident map from to linear operators on the Fock space equipped with their operator product is an associative algebra isomorphism onto its image:
(Dütsch 18, theorem 2.17, following Dütsch-Fredenhagen 00,, pages 10-11, Dütsch-Fredenhagen 01)
Related concepts
References
Original articles include
-
Gian-Carlo Wick, The evaluation of the collision matrix, Phys. Rev. 80, 268-272 (1950)
-
Klaus Hepp, Théorie de la Renormalisation Lect. Notes in Physics, Springer 1969
-
Romeo Brunetti, Klaus Fredenhagen, Rainer Verch, theorem 2.4 in The generally covariant locality principle – A new paradigm for local quantum physics, Commun.Math.Phys.237:31-68, 2003 (arXiv:math-ph/0112041)
The interpretation as an algebra isomorphism to the star product with respect to the Wightman propagator is made explicit in
-
Michael Dütsch, Klaus Fredenhagen, pages 10-11 of Algebraic Quantum Field Theory, Perturbation Theory, and the Loop Expansion, Commun.Math.Phys. 219 (2001) 5-30 (arXiv:hep-th/0001129)
-
Michael Dütsch, Klaus Fredenhagen, Perturbative algebraic quantum field theory and deformation quantization, Proceedings of the Conference on Mathematical Physics in Mathematics and Physics, Siena June 20-25 (2000) (arXiv:hep-th/0101079)
Textbook accounts include
-
Günter Scharf, theorem 3.1 in Finite Quantum Electrodynamics – The Causal Approach, Berlin: Springer-Verlag, 1995, 2nd edition
-
Michael Dütsch, E.26 - E.30 in From classical field theory to perturbative quantum field theory, 2018
See also
- Wikipedia, Wick’s theorem
Discussion of Wick’s lemma as a consequence of the homological perturbation lemma for BV-complexes is in
- Owen Gwilliam, section 2.3 Factorization algebras and free field theories PhD thesis (pdf)
Formalization of Wick’s theorem in the proof assistant Lean:
- Joseph Tooby-Smith: Digitalizing Wick’s theorem [arXiv:2505.07939]
Last revised on May 14, 2025 at 04:59:20. See the history of this page for a list of all contributions to it.