nLab Feynman diagram
Context
Algebraic Qunantum Field Theory
algebraic quantum field theory (perturbative, on curved spacetimes, homotopical)
Concepts
quantum mechanical system, quantum probability
interacting field quantization
Theorems
States and observables
Operator algebra
Local QFT
Perturbative QFT
Measure and probability theory
Measure theory
Probability theory
Information geometry
Thermodynamics
Theorems
Applications
Contents
Idea
General
For a Gaussian probability measure and a perturbation with polynomial at least of degree 3, there is a combinatorial expression for the moments/expectation values of as a sum over certain graphs whose -ary vertices are labeled by the monomials of degree in . (This is such that for it reduces to Wick's lemma.)
These graphs are called Feynman diagrams.
In perturbative quantum field theory
Feynman graphs play a central role in perturbative quantum field theory, where plays the role of an action functional on a space of fields, is the exponentiated kinetic action and hence the measure for free fields, while is the interaction part of the action functional: the order- monomials in encode an interaction of fields. In this context the corresponding Feynman diagrams are traditionally thought of as depicting interaction processes of quanta of these fields, with propagation along the edges and interaction at the vertices. But this interpretation has its limits, which is partly reflected in speaking of “virtual particles”. A precise interpretation is given by worldline formalism.
Details
For finitely many degrees of freedoms
We discuss Feynman diagrams for a single real scalar field on a discrete space of points. This contains in it already all the aspects of real Feynman diagrams in perturbative quantum field theory and in this context everything is easily well-defined. The generalization to more field components is immediate and simply obtained by thinking of all “” in the following as taking values in some appropriate representation space and all products of s as given by suitable intertwiners and inner products, otherwise the form of the formulas remains the same. Similarly, in generalization to continuous space (non-finitely many degrees of freedom) all the diagrammatics remains the same, the only issue now is to make sense (namely via renormalization) of the numerical value that is assigned to any one Feynman diagram.
So a field here is a map from the -element finite set to the real numbers, and hence the space of all field configurations is .
Fix then a real-valued matrix of non-vanishing determinant .
For standard applications this is a discretized version of the Laplacian and then the expression
is the kinetic energy and kinetic action of the field configuration . More concretely, think of the set of space points as being a discretization of a circle and write for the corresponding (discrete) Fourier transform of . Then the kinetic term of the free scalar field on this space is given by which is the diagonal matrix in the -basis with
where is a constant called the mass of the field .
A sum over all values of is the finite (and hence well-defined) analog of a path integral. The Gaussian integral of is called the partition function:
An n-point function is an th moment of this Gaussian distribution:
In order to compute these conveniently, pass to the generating function obtained by adding a source variable :
where is the inverse matrix of , which appears by computing the new integral here again as a Gaussian integral after completing the square in the exponent.
In applications to field theory this is called the Feynman propagator. In the standard example where is the kinetic term of the free field of mass then in Fourier-transformed components is diagonal with components
This means, incidentally. that in the non-finite case of interest in physics, is not actually naively invertible after all, as on the mass shell. In this case one has to replace the naive with its zeta-function regularized version.
The way this works is insightful even when the naive does exist. Notice that using “Schwinger parameterization” the propagator is equivalently rewritten as a Mellin transform integral:
Again in the example of the standard scalar field kinetic term expressed in Fourier diagonalization then with a parameterization of the straight line with slope , the exponent is equivalently
This now happens to be the standard action functional (Polyakov action) for a sigma model describing the propagation of a particle along its worldline. This means that the propagator of the scalar field may be thought of as coming from the path integral of a scalar particle along its worldline. This perspective is called the “worldline formalism”, it is a formalization of second quantization, expressing the dynamics of fields in terms of that of their particle “quanta” running along worldlines of the form of the corresponding Feynman diagrams (to which we finally come in a moment).
Back to the computation of the -point function. By construction, it is now equally expressed by partial derivatives of the generating function with respect to the source variable and evaluated at , and this in turn is a combinatorial expression just in products of the propagator:
Here the last equality – known as Wick's theorem – comes from simple inspection: take the derivatives inside the exponential series and observe that then the only summands non-vanishing at appears for even and are those where all derivatives hit the monomial .
Thinking of here as labeling an edge (a “worldline”) from vertex to vertex This is the source of all Feynman digrammatics.
Now consider a polynomial of degree . In applications to field theory this represents the potential energy or (self)interaction of the field configuration. The difference of the kinetic energy and the potential energy is called the (here: “Wick rotated”/“Euclidean”) action
The prefactor is called the coupling constant.
Putting everything together, the integral over the full action may be expressed as a power series in the coupling constant of the moments with respect to the kinetic action of the powers of the interaction term:
By Wick's theorem stated above, each is equivalently expressed as a sum over products of components of the propagator . Thinking of each such propagator term as an edge produces a diagram, this is the corresponding Feynman diagram.
For instance, for a cubic point interaction
then
Here the first summand corresponds to the “dumbbell” Feynman diagram of the form
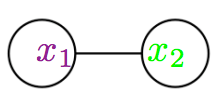
and the second summand corresponds to the “theta” Feynman diagram of the form
 .
.
In perturbative quantum field theory
For details see at
- S-matrix the section Feynman perturbation series
| free field algebra of quantum observables | physics terminology | maths terminology | |
|---|---|---|---|
| 1) | supercommutative product | normal ordered product | pointwise product of functionals |
| 2) | non-commutative product (deformation induced by Poisson bracket) | operator product | star product for Wightman propagator |
| 3) | time-ordered product | star product for Feynman propagator | |
| perturbative expansion of 2) via 1) | Wick's lemma  | Moyal product for Wightman propagator | |
| perturbative expansion of 3) via 1) | Feynman diagrams 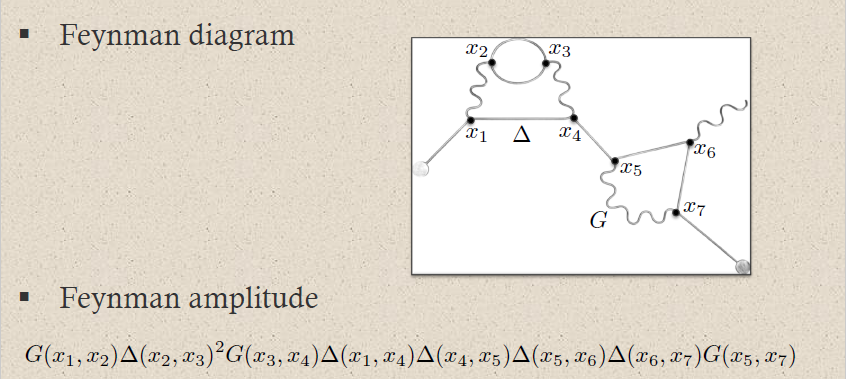 | Moyal product for Feynman propagator |
Example
(Feynman amplitudes in causal perturbation theory – example of QED)
In perturbative quantum field theory, Feynman diagrams are labeled multigraphs that encode products of Feynman propagators, called Feynman amplitudes (this prop.) which in turn contribute to probability amplitudes for physical scattering processes – scattering amplitudes:
The Feynman amplitudes are the summands in the Feynman perturbation series-expansion of the scattering matrix
of a given interaction Lagrangian density .
The Feynman amplitudes are the summands in an expansion of the time-ordered products of the interaction with itself, which, away from coincident vertices, is given by the star product of the Feynman propagator (this prop.), via the exponential contraction
Each edge in a Feynman diagram corresponds to a factor of a Feynman propagator in , being a distribution of two variables; and each vertex corresponds to a factor of the interaction Lagrangian density at .
For example quantum electrodynamics in Gaussian-averaged Lorenz gauge involves (via this example):
-
the Dirac field modelling the electron, with Feynman propagator called the electron propagator (this def.), here to be denoted
-
the electromagnetic field modelling the photon, with Feynman propagator called the photon propagator (this prop.), here to be denoted
The Feynman diagram for the electron-photon interaction alone is
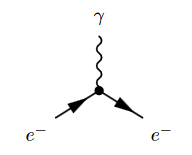
where the solid lines correspond to the electron, and the wiggly line to the photon. The corresponding product of distributions is (written in generalized function-notation)
Hence a typical Feynman diagram in the QED Feynman perturbation series induced by this electron-photon interaction looks as follows:

where on the bottom the corresponding Feynman amplitude product of distributions is shown; now notationally suppressing the contraction of the internal indices and all prefactors.
For instance the two solid edges between the vertices and correspond to the two factors of :

This way each sub-graph encodes its corresponding subset of factors in the Feynman amplitude:


graphics grabbed from Brouder 10
A priori this product of distributions is defined away from coincident vertices: . The definition at coincident vertices requires a choice of extension of distributions to the diagonal locus. This choice is the ("re-")normalization of the Feynman amplitude.
Related concepts
References
General
Traditional review:
-
Radovan Dermisek: Path integral for interacting field (2009) [pdf]
-
Stefan Weinzierl: Introduction to Feynman Integrals [arXiv:1005.1855]
-
Stefan Weinzierl: Feynman Integrals, UNITEXT for Physics, Springer (2022) [arXiv:2201.03593, doi:10.1007/978-3-030-99558-4]
-
Stefan Weinzierl: Feynman Diagrams, Encyclopedia of Particle Physics (2025) [arXiv:2501.08354]
See also
-
Alain Connes, Matilde Marcolli, section 3 of Noncommutative Geometry, Quantum Fields and Motives
-
Wikipedia, Feynman diagram
-
F. T. Brandt, J. Frenkel, D. G. C. McKeon, Feynman diagrams in terms of on-shell propagators [arXiv:2206.14860]
-
Zhi-Feng Liu, Yan-Qing Ma, Determining Feynman Integrals with Only Input from Linear Algebra, Physical Review Letters, Volume 129, Issue 22, 23 November 2022 (doi:10.1103/PhysRevLett.129.222001, arXiv:2201.11637)
Discussion via D-modules:
- Johannes Henn, Elizabeth Pratt, Anna-Laura Sattelberger, Simone Zoia, -Module Techniques for Solving Differential Equations in the Context of Feynman Integrals [arXiv:2303.11105]
In causal perturbation theory
Discussion of Feynman diagrams in the rigorous formulation of causal perturbation theory and perturbative AQFT is due to
- Kai Keller, chapter IV of Dimensional Regularization in Position Space and a Forest Formula for Regularized Epstein-Glaser Renormalization, PhD thesis (arXxiv:1006.2148)
parts of which also appears as
- Michael Dütsch, Klaus Fredenhagen, Kai Keller, Katarzyna Rejzner, Dimensional Regularization in Position Space, and a Forest Formula for Epstein-Glaser Renormalization, J. Math. Phy.
55(12), 122303 (2014) (arXiv:1311.5424)
An exposition of this is in
- Christian Brouder, Multiplication of distributions, 2010 (pdf)
Relation to the Hopf algebra structure on Feynman diagrams due to Kreimer 97 is discussed in
- Jose Gracia-Bondia, S. Lazzarini, Connes-Kreimer-Epstein-Glaser Renormalization (arXiv:hep-th/0006106)
Relation to periods (in the sense here) is discussed in
- Kasia Rejzner, Renormalization and periods in perturbative Algebraic Quantum Field Theory (arXiv:1603.02748)
See also
- Eli Hawkins, Kasia Rejzner, section 5.2 of The Star Product in Interacting Quantum Field Theory (arXiv:1612.09157)
Review is in
- Katarzyna Rejzner, section 6.5.2 of Perturbative Algebraic Quantum Field Theory, Mathematical Physics Studies, Springer 2016 (pdf)
In terms of motivic structures
In terms of motives (see also motives in physics)
-
Spencer Bloch, Helene Esnault, Dirk Kreimer, On motives associated to graph polynomials, (pdf)
-
Spencer Bloch, Pierre Vanhove, The elliptic dilogarithm for the sunset graph, IHES preprint P-13-24, pdf
In homological BV-quantization
A clean derivation of the Feynman rules for finite-dimensional spaces of fields in terms of quantization by passing to cochain cohomology of BV-complexes (see at BV-formalism – Homological quantization) is in
- Owen Gwilliam, Theo Johnson-Freyd, How to derive Feynman diagrams for finite-dimensional integrals directly from the BV formalism (2011) (arXiv:1202.1554)
with a review in the broader context of factorization algebras of observables in section 2.3 of
- Owen Gwilliam, Factorization algebras and free field theories (pdf)
As string diagrams (morphisms in monoidal categories)
It has been observed that Feynman diagrams, notably in gauge theory, are in particular string diagrams (in the sense of category theory, not here in any sense of string theory!) in the given category of representations: the edges are labelled by particle species, hence by Wigner classification by irreps, and the vertices are labeled by representation homomorphisms (“intertwiners”) which, indeed, label the interaction of particles in the Feynman diagram.
A review of this formulation is in
- John Baez, Aaron Lauda, A Prehistory of n-Categorical Physics, Deep beauty, 13-128, Cambridge Univ. Press, Cambridge, 2011 (arXiv:0908.2469)
Moreover, one may think of string diagrams in monoidal categories as providing categorical semantics for proof nets (see there for more) in multiplicative linear logic. Under this identification then Feynman diagrams have a relation to proof nets. Something like this is discussed in
- Richard Blute, Prakash Panangaden, Proof nets as formal Feynman diagrams (pdf)
Last revised on January 16, 2025 at 11:28:01. See the history of this page for a list of all contributions to it.