nLab bimonoid

Idea

A bimonoid is something which is both a monoid and a comonoid in a compatible way. The compatibility is easy to formulate in symmetric monoidal categories and much harder in a nonsymmetric setup.

Definition in symmetric monoidal categories

In a symmetric monoidal category, a bimonoid (or bimonoid object) is an object $B$ equipped with a structure of a monoid and a comonoid which are compatible in one of two equivalent ways: the comultiplication and the counit are morphisms of monoids or the multiplication and the unit are morphisms of comonoids. The symmetry of the monoidal structure is involved in the definition of the tensor product $B\otimes B$ as monoids and as comonoids. In terms of string diagrams, the equations expressing the compatibility of the monoidal and comonoidal structures on $B$ may be represented as follows:

                    

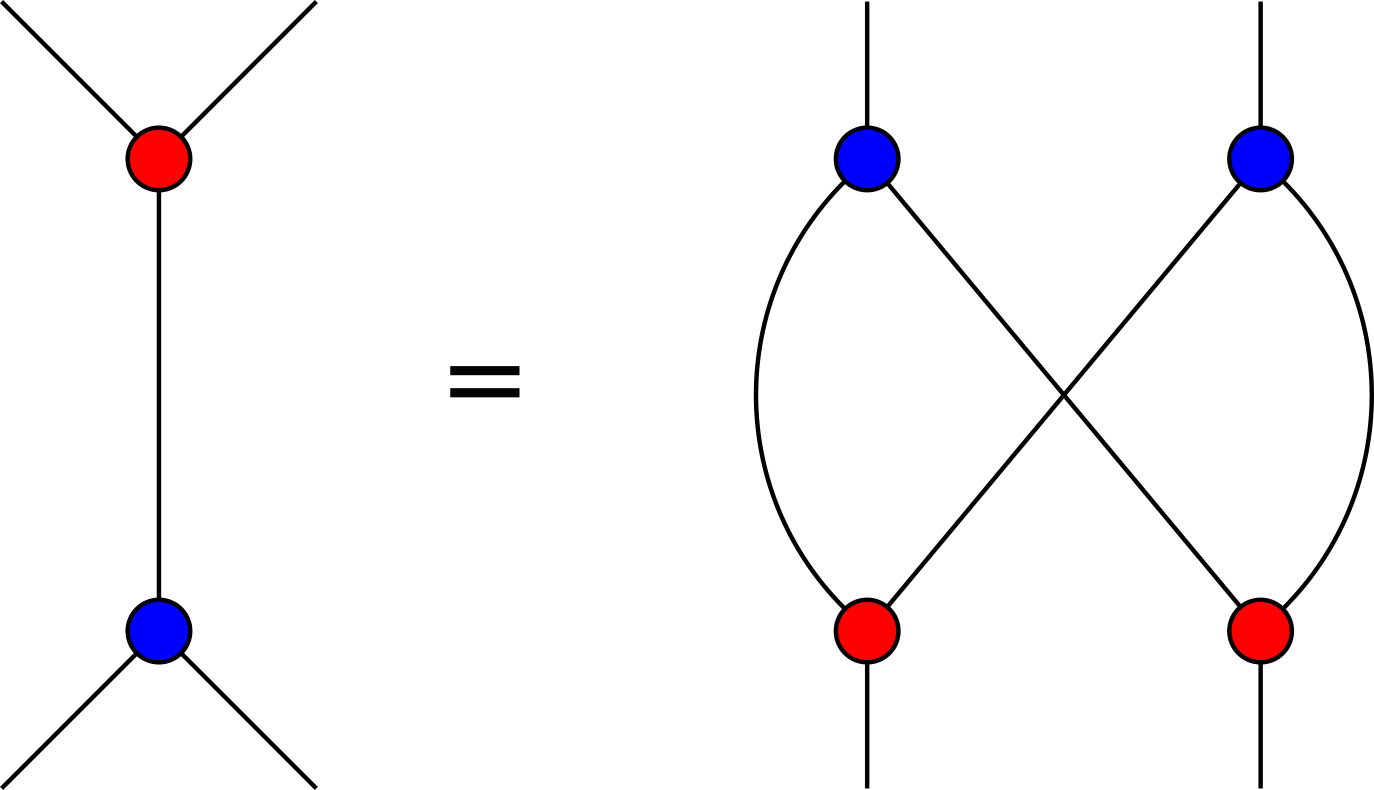
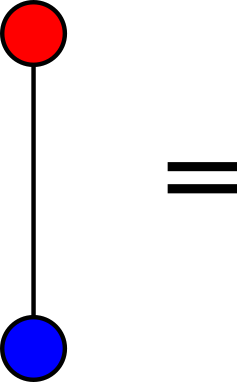
A bimonoid that additionally has an antipode (a map $s \colon B\to B$ satisfying an axiom that makes it act like “inverses” in a group) is called a Hopf monoid; a Hopf monoid in Vect is a Hopf algebra.

A bimonoid that is both a commutative monoid and a cocommutative comonoid is called bicommutative.

Examples

• A bimonoid in Vect (with its usual tensor product) is generally called a bialgebra.

• In a category with biproducts, with the biproduct as the monoidal product, every object is a bimonoid in a unique way (Café post). This bimonoid is bicommutative.

• More generally, in a cartesian monoidal category, every monoid object is a bimonoid in a unique way, with comultiplication being the diagonal map. Dually, every comonoid object in a cocartesian monoidal category is a bimonoid in a unique way.

• A bimonoid is said to be special if comultiplication followed by multiplication is the identity. The category Rel has biproducts so every object is a bicommutative bimonoid, but these bimonoids are also special. The category FinRel is the free symmetric monoidal category on a special bicommutative bimonoid, namely $1$ with its diagonal as comultiplication and fold map as multiplication.

• A bimonoid is said to be connected if counit followed by unit is the identity. For example, the symmetric algebra is a connected bimonoid.

• One obtains the notion of quasi-bimonoid by omitting the associativity and coassociativity requirements.

Monoidal structure on modules

If $B$ is a bimonoid in $\mathcal{C}$, then the category $Mod_B$ of $B$-modules inherits a monoidal structure such that the forgetful functor $Mod_B \to \mathcal{C}$ (the “fiber functor”) is a strong monoidal functor. For $B$-modules $M$ and $N$, we equip the tensor product $M\otimes N$ in $\mathcal{C}$ with the $B$-action given by

$$B\otimes (M\otimes N) \xrightarrow{\Delta} (B\otimes B) \otimes (M\otimes N) \xrightarrow{\cong} (B\otimes M) \otimes (B\otimes N) \xrightarrow{act \otimes act} M\otimes N$$

where $\Delta$ denotes the comultiplication of $B$ as a comonoid. The bimonoid compatibility axioms are exactly what is needed to make this a $B$-module structure, and coassociativity makes it associative. Similarly, we use the counit $B\to I$ of $B$ to give the unit object $I$ a $B$-module structure.

If $B$ moreover a Hopf monoid, then $Mod_B$ also inherits a closed monoidal structure if $\mathcal{C}$ has one; see at Hopf monoid.

These relations are known as Tannaka duality for monoids/algebras, see at structure on algebras and their module categories - table.

Non-symmetric variants

It is interesting how to generalize this notion in various nonsymmetric situations, for example involving braidings, or more generally in duoidal categories, or in relative situations over noncommutative rings (e.g. Takeuchi bialgebroids). In the completely noncommutative situation of the monoidal category of endofunctors, one can look at various compatibilities between monads and comonads or monads and tensor products, for example involving mixed distributive laws.

Related concepts

• Hopf monoid, Frobenius monoid, graded bimonoid

References

As far as compatibility with tensor product is concerned, there is a notion of a bimonad and involves a version of distributive laws, hence it is related to a lifting problem:

• Ieke Moerdijk, Monads on tensor categories, Category theory 1999 (Coimbra), J. Pure Appl. Algebra 168 (2002), no. 2-3, 189–208 (MR2003e:18012)

• Kornél Szlachányi, The monoidal Eilenberg–Moore construction and bialgebroids, J. Pure Appl. Algebra 182, no. 2–3 (2003) 287–315; Adjointable monoidal functors and quantum groupoids, math.QA/0301253

Szlachányi uses earlier analysis of

• P. Schauenburg, Bialgebras over noncommutative rings, and a structure theorem for Hopf bimodules, Applied Categorical Structures 6, 193-222 (1998) doi

• H.E. Porst, On categories of monoids, comonoids and bimonoids, Quaest. Math. 31 (2008) 127-139 MR2010d:18010 doi

For a dual version see

• P. Mac Crudden, Opmonoidal monads, Theory Appl. Cat., Vol. 10, 2002, No. 19, pp 469-485, link

There is also a more subtle notion also called Hopf monad in

• R. Wisbauer, B. Mesablishvili, Bimonads and Hopf monads on categories, arXiv:0710.1163

In some of these generalized cases, one does not have a good notion of of antipode, so that the difference between bimonoids and Hopf monoids has to be stated in different terms. A similar case is in the case of Hopf algebroids over a noncommutative base:

• Brian Day, Ross Street, Monoidal bicategories and Hopf algebroids, Advances in Math. 129, 1 (1997) 99–157

• Gabi Böhm, Hopf algebroids, (a chapter of) Handbook of algebra, arxiv:math.RA/0805.3806; An alternative notion of Hopf algebroid; in “Hopf algebras in noncommutative geometry and physics”, 31–53, Lec. Notes in Pure and Appl. Math. 239, Dekker, New York 2005; math.QA/0301169

The fact that a skeleton of FinRel is the PROP for special bicommutative bimonoids is Theorem 7.2 in Coya and Fong, based on techniques from Lack’s paper on distributive laws for PROPs:

• Brandon Coya and Brendan Fong, Corelations are the prop for extraspecial commutative Frobenius monoids, Theory and Applications of Categories, Vol. 32, 2017, No. 11, pp. 380-395. (arxiv)

• Steve Lack, Composing PROPs, Theory and Applications of Categories 13(9):147–163, 2004. (pdf)