nLab distributive law

Idea

Sometimes in mathematics one considers objects equipped with two different types of extra structure which interact in a suitable way. For instance, a ring is a set equipped with both (1) the structure of an (additive) abelian group and (2) the structure of a (multiplicative) monoid, which satisfy the distributive laws $a\cdot (b+c) = a\cdot b + a\cdot c$ and $a\cdot 0 = 0$.

Abstractly, there are two monads on the category Set, one (call it $\mathbf{T}$) whose algebras are abelian groups, and one (call it $\mathbf{S}$) whose algebras are monoids, and so we might ask “can we construct, from these two monads, a third monad whose algebras are rings?” Such a monad would assign to each set $X$ the free ring on that set, which consists of formal sums of formal products of elements of $X$—in other words, it can be identified with $T(S(X))$. Thus the question becomes “given two monads $\mathbf{T}$ and $\mathbf{S}$, what further structure is required to make the composite $T S$ into a monad?”

It is easy to give $T S$ a unit, as the composite $Id \xrightarrow{\eta^S} S \xrightarrow{\eta^T S} T S$, but to give it a multiplication we need a transformation from $T S T S$ to $T S$. We naturally want to use the multiplications $\mu^T\colon T T \to T$ and $\mu^S\colon S S \to S$, but in order to do this we first need to switch the order of $T$ and $S$. However, if we have a transformation $\lambda\colon S T \to T S$, then we can define $\mu^{T S}$ to be the composite $T S T S \xrightarrow{\lambda} T T S S \xrightarrow{\mu^T\mu^S} T S$.

Such a transformation, satisfying suitable axioms to make $T S$ into a monad, is called a distributive law, because of the motivating example relating addition to multiplication in a ring. In that case, $S T X$ is a formal product of formal sums such as $(x_1 + x_2 + x_3)\cdot (x_4 + x_5)$, and the distributive law $\lambda$ is given by multiplying out such an expression formally, resulting in a formal sum of formal products such as $x_1\cdot x_4 + x_1 \cdot x_5 + x_2 \cdot x_4 + x_2 \cdot x_5 + x_3\cdot x_4 + x_3 \cdot x_5$.

Remark

(terminology – what distributes over what)
The eponymous example of distributivity in arithmetic

$$a \times \sum_i b_i \;=\; \sum_i a \times b_i$$

hence

$$\big( a \times (-) \big) \circ \big( \sum (-) \big) \;\; = \;\; \big( \sum (-) \big) \circ \big( a \times (-) \big)$$

(where, of course, the equality as such works in both directions, but the distribution of factors over summands is the step from left to right) suggests that a suitable transformation of (co)monads of the form

$$T_1 \circ T_2 \longrightarrow T_2 \circ T_1$$

should be referred to as $T_1$ distributing over $T_2$ instead of the other way around.

However, already the original reference Beck 1969 §1 uses the opposite terminology.

Authors sticking to this original but arguably reverse terminological convention include Brookes & Van Stone 1993, while other authors tacitly switch to the other terminological convention (eg. Barr & Wells 1985 §9 2.1, Power & Watanabe 2002 p. 138).

Big picture

Monads in any 2-category $C$ make themselves a 2-category $\mathrm{Mnd}$ in which 1-morphisms are either lax or colax homomorphisms of monads (cf. monad transformations). By formal duality the analogue is true for comonads.

Distributivity laws may be understood as monads internal to this 2-category of monads.

In particular, distributive laws themselves make a 2-category.

There are other variants like distributive laws between a monad and an endofunctor, “mixed” distributive laws between a monad and a comonad (the variants for algebras and coalgebras called entwining structures), distributive laws between actions of two different monoidal categories on the same category, for PROPs and so on.

Having a distributive law $l$ from one monad to another enables to define the composite monad $\mathbf T\circ_l\mathbf P$. This correspondence extends to a 2-functor $\mathrm{comp} \,\colon\, \mathrm{Mnd}(\mathrm{Mnd}(C))\to\mathrm{Mnd}(C)$. An analogue of this 2-functor in the mixed setup is a 2-functor from the bicategory of entwinings to a bicategory of corings.

Explicit definition

Monad distributing over monad

A distributive law for a monad $\mathbf{T} = (T, \mu^T, \eta^T)$ in $A$ over an endofunctor $P$ is a 2-morphisms $l : T P \Rightarrow P T$ such that $l \circ (\eta^T)_P = P(\eta^T)$ and $l \circ (\mu^T)_P = P(\mu^T) \circ l_T \circ T(l)$. In diagrams:

Distributive laws for the monad $\mathbf{T}$ over the endofunctor $P$ are in a canonical bijection with lifts of $P$ to an endofunctor $P^{\mathbf T}$ in the Eilenberg-Moore category $A^{\mathbf T}$, satisfying $U^{\mathbf T} P^{\mathbf T} = P U^{\mathbf T}$. Indeed, the endofunctor $P^{\mathbf T}$ is given by $(M,\nu) \mapsto (P M,P(\nu)\circ l_M)$.

A distributive law for a monad $\mathbf{T} = (T, \mu^T, \eta^T)$ over a monad $\mathbf{P} = (P, \mu^P, \eta^P)$ in $A$ is a distributive law for $\mathbf T$ over the endofunctor $P$, compatible with $\mu^P,\eta^P$ in the sense that $l \circ T(\eta^P) = (\eta^P)_T$ and $l \circ T(\mu^P) = (\mu^P)_T \circ P(l) \circ l_P$. In diagrams:

(due to Beck 1969, review includes Barr & Wells 1985 §9 2.1)

The correspondence between distributive laws and endofunctor liftings extends to a correspondence between distributive laws and monad liftings. That is, distributive laws $l : T P \Rightarrow P T$ from the monad $\mathbf{T}$ to the monad $\mathbf{P}$ are in a canonical bijection with lifts of the monad $\mathbf{P}$ to a monad $\mathbf{P}^{\mathbf T}$ in the Eilenberg-Moore category $A^{\mathbf T}$, such that $U^{\mathbf T} : A^{\mathbf T}\to A$ preserves the monad structure.

Thus all together a distributive law for a monad over a monad is a 2-cell for which 2 triangles and 2 pentagons commute. In the entwining case, Brzeziński and Majid combined the 4 diagrams into one picture which they call the bow-tie diagram.

Monad distributing over a comonad

van Osdol 1973 p. 456

(…)

Comonad distributing over monad

The distributivity law of

• a comonad $\mathcal{C}$ over

• a monad $\mathcal{E}$

on the same category $\mathbf{C}$

is as follows (Brookes & Van Stone 1993 Def. 3, Power & Watanabe 2002):

A natural transformation

$$distr^{\mathcal{C}, \mathcal{E}}_{(\text{-})} \;\;\colon\;\; \mathcal{C} \big( \mathcal{E}(-) \big) \longrightarrow \mathcal{E} \big( \mathcal{C}(-) \big)$$

such that the following diagrams commute for all objects $D$:

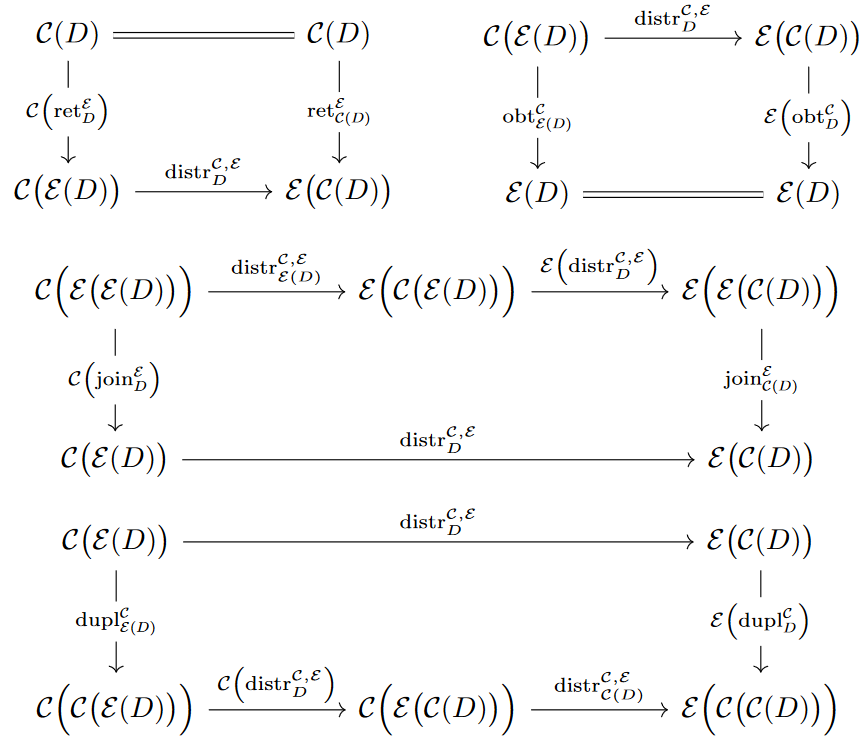
Given this distributivity structure, there is a two-sided (“double”) Kleisli category (Brookes & Van Stone 1993 Thm. 2, Power & Watanabe 2002, Prop. 7.4) whose objects are those of $\mathbf{C}$, and whose morphisms $D_1 \to D_2$ are morphisms in $\mathbf{C}$ of the form

$$prog_{12} \;\colon\; \mathcal{C}(D_1) \longrightarrow \mathcal{E}(D_2)$$

with two-sided Kelisli composition

$$prog_{12} \text{>=>} prog_{23} \;\; \colon \;\; \mathcal{C}(D_1) \longrightarrow \mathcal{E}(D_3)$$

given by the (co-)bind-operation on the factors connected by the distributivity transformation:

Examples

Products distributing over coproducts

In a distributive category products distribute over coproducts.

In Cat

• There is a distributive law of the monad (on Set) for monoids over the monad for abelian groups, whose composite is the monad for rings. This is the canonical example which gives the name to the whole concept.

Tensor products distributing over direct sums

For many standard choices of tensor products in the presence of direct sums the former distribute over the latter. See at tensor product of abelian groups and tensor product of modules.

In other 2-categories

• strict factorization systems can be identified with distributive laws between categories regarded as monads in Span(Set).

• More generally, factorization systems over a subcategory can be identified with distributive laws in Prof. Ordinary orthogonal factorization systems are a special case. The latter can also be obtained by other weakenings; see for instance this discussion.

Related concepts

• weak distributive law

• iterated distributive law

• wreath

• distributivity for monoidal structures

• monad transformer

• pseudo-distributive law

Literature

• Jon Beck, Distributive Laws, in: Seminar on Triples and Categorical Homology Theory, ETH 1966/67, Lecture Notes in Mathemativs, Springer (1969), Reprints in Theory and Applications of Categories 18 (2008) 1-303 [TAC:18, pdf]

• Donovan van Osdol, Bicohomology Theory, Transactions of the American Mathematical Society 183 (1973) 449-476 [jstor:1996479]

• Ross Street, §6 of: The formal theory of monads, Journal of Pure and Applied Algebra 2 2 (1972) 149-168 [doi:10.1016/0022-4049(72)90019-9]

• Michael Barr, Charles Wells, Toposes, Triples, and Theories, Springer (1985) republished in: Reprints in Theory and Applications of Categories, 12 (2005) 1-287 [tac:tr12, tac:tr12]

• Stephen Brookes, Kathryn Van Stone, Monads and Comonads in Intensional Semantics (1993) [dtic:ADA266522, pdf, pdf]

• Martin Markl, Distributive laws and Koszulness, Ann. Inst. Fourier (Grenoble) 46 (1996), no. 2, 307–323 (numdam)

• T. F. Fox, Martin Markl, Distributive laws, bialgebras, and cohomology, Operads: Proceedings of Renaissance Conferences (Hartford, CT/Luminy, 1995), Contemp. Math. 202 AMS (1997) 167-205

• T. Brzeziński, S. Majid, Coalgebra bundles, Comm. Math. Phys. 191 2 (1998) 467–492 [arXiv:q-alg/9602022]

• John Power, Hiroshi Watanabe, Distributivity for a monad and a comonad, Electronic Notes in Theoretical Computer Science 19 (1999) 102 [doi:10.1016/S1571-0661(05)80271-3, pdf]

• Steve Lack, Composing PROPS, Theory Appl. Categ. 13 (2004), No. 9, 147–163.

• Steve Lack, Ross Street, The formal theory of monads II, Special volume celebrating the 70th birthday of Professor Max Kelly, J. Pure Appl. Algebra 175 1-3 (2002) 243-265

• John Power, Hiroshi Watanabe, Combining a monad and a comonad, Theoretical Computer Science 280 1–2 (2002) 137-162 [doi:10.1016/S0304-3975(01)00024-X]

• T. Brzeziński, Robert Wisbauer, Corings and comodules, London Math. Soc. Lec. Note Series 309, Cambridge (2003)

• Gabi Böhm, Internal bialgebroids, entwining structures and corings, AMS Contemp. Math. 376 (2005) 207-226 [arXiv:math.QA/0311244]

• Zoran Škoda, Distributive laws for monoidal categories (arXiv:0406310); Equivariant monads and equivariant lifts versus a 2-category of distributive laws (arXiv:0707.1609); Bicategory of entwinings (arXiv:0805.4611)

• R. Wisbauer, Algebras versus coalgebras, Appl. Categ. Structures 16 1-2 (2008) 255–295 [doi:10.1007/s10485-007-9076-5]

• Zoran Škoda, Some equivariant constructions in noncommutative geometry, Georgian Math. J. 16 (2009) 1; 183–202 (arXiv:0811.4770)

• Bachuki Mesablishvili, Robert Wisbauer, Bimonads and Hopf monads on categories, Journal of K-Theory 7 2 (2011) 349-388 [arXiv:0710.1163, doi:10.1017/is010001014jkt105]

• Francisco Marmolejo, Adrian Vazquez-Marquez, No-iteration mixed distributive laws, Mathematical Structures in Computer Science 27 1 (2017) 1-16 [doi:10.1017/S0960129514000656]

• Liang Ze Wong, Distributive laws, post at $n$-cafe, Feb 2017

• Enrique Ruiz Hernández, Another characterization of no-iteration distributive laws, arxiv

On distributive laws for relative monads:

• Gabriele Lobbia, Distributive Laws for Relative Monads, Applied Categorical Structures 31 19 (2023) [doi:10.1007/s10485-023-09716-1, arXiv:2007.12982]