nLab context-free grammar

Idea

The notion of context-free grammar, now used in linguistics, computer science and mathematics, was introduced in the works of Noam Chomsky.

Traditional definition

We write $X + Y$ for the disjoint union of two sets and use vector notation and the Kleene star $\vec{v} \in X^\star$ to denote sequences in the free monoid.

A context-free grammar is a tuple $(\Sigma, X, R, s)$ where $\Sigma$ and $X$ are finite sets called the vocabulary (also called the terminals) and the non-terminals respectively, $R \subseteq X \times (X + \Sigma)^\star$ is a finite set of production rules and $s \in X$ is called the start symbol.

The language of a context-free grammar is given by $L(G) = \{ \vec{u} \in V^\star \vert s \to_R \vec{u} \}$ where the rewriting relation $(\to_R) \subseteq (V + X)^\star \times (V + X)^\star$ is traditionally defined as the transitive closure of the following directed graph:

$$\big\{ (\vec{u} x \vec{w}, \vec{u v w}) \quad \vert \quad \vec{u}, \vec{w} \in (V + X)^\star, (x, \vec{v}) \in R \big\}$$

With string diagrams

One may redefine $L(G) = \big\{ \vec{u} \in \Sigma^\star \vert \C_G(s, \vec{u}) \neq \emptyset \big\}$ where $C_G$ is the free monoidal category with:

• generating objects the disjoint union $\Sigma + X$,
• generating arrows the production rules $(x, \vec{v}) \in R$ with $dom(x, \vec{v}) = x$ and $cod(x, \vec{v}) = \vec{v}$.

That is, a string $\vec{u} \in \Sigma^\star$ is grammatical whenever there exists an arrow from the start symbol $s$ to $\vec{u}$ in $C_G$. Arrows in $C_G$ may be encoded as a syntax tree, seen as a special case of a string diagram, e.g.:

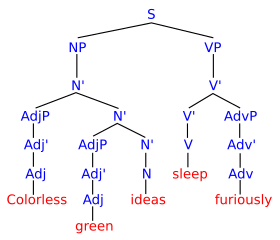
Note that context-free grammar is weakly equivalent to Lambek's pregroup grammar i.e. they generate the same class of languages, see:

• Wojciech Buszkowski, Katarzyna Moroz, Pregroup Grammars and Context-free Grammars, Computational Algebraic Approaches to Natural Language, Polimetrica (2008) (pdf)

Early sources

Here is list of some of the original references in English and also of their Russian translations.

• N. Chomsky, Three models for the description of language, I. R. E. Trans. PGIT 2 (1956), 113—124. (Русский перевод: Хомский Н., Три модели для описания языка, Кибернетический сборник, вып. 2, ИЛ 1961, 237-266)
• N. Chomsky, On certain formal properties of grammars, Information and Control 2 (1959), 137—267; A note on phrase structure grammars, Information andControl 2 1959_, 393—395. (Хомский К, Заметки o грамматиках непосредственных составляющих. Кибернетический сборник, вып. 5, ИЛ, 1962, 312—315.)
• N. Chomsky, On the notion «Rule of Grammar», Proc. Symp. Applied Math., 12. Amer. Math. Soc. (1961). (Хомский Н., О понятии «правило грамматики», сб. Новое в лингвистике, вып. 4, «Прогресс», 1965, стр. 34—65.)
• N. Chomsky, Context-free grammars and pushdown storage, Quarterly Progress Reports, № 65, Research Laboratory of Electronics, M. I. T., 1962.
• N. Chomsky, Formal properties of grammars, in Handbook of Mathemati- Mathematical Psychology, 2, ch. 12, Wiley, 1963, p. 323—418. (Хомский Н., Формальные свойства грамматик, Кибернетический сборник, вып. 2, «Мир», 1966, 121—-230.)
• N. Chomsky, The logical basis for linguistic theory, Proc. IX-th Int. Cong. Linguists (1962). (Хомский Н“ Логические основы лингвистической теории, сб. Новое в лингвистике, вып. 4, «Прогресс», 1965, 465—-575.)
• N. Сhоmskу, G. A. Miller G. A.. Finite state languages, Information and Control 1 (1958), 91—-112. (Хомский Н., Миллер Д., Языки с конечным числом состояний, Кибернетический сборник, вып. 4, ИЛ, 1962, 231—-255.), Introduction to the formal analysis of natural languages. Handbook of Mathematical Psychology 2, Ch. 12, Wiley, 1963, 269—-322 (Введение в формальный анализ естественных языков, Кибернетический сборник, вып. 1, «Мир», 1965, стр. 229—-290.)
• N. Chomsky, M. P. Schützenberger, The algebraic theory of context-free languages, in: Computer programming and formal systems, 118–161 North-Holland 1963, Amsterdam MR152391 (Кибернетический сборник 3, 195–242, 1966)

Modern literature

• wikipedia: context-free language
• A. V. Aho, J. D. Ullman, The theory of parsing, translation, and compiling, vol 1, Parsing; vol. 2, Compiling. Prentice Hall, 1972.
• A. V. Aho, J. D. Ullman, Principles of compiler design, Addison-Wesley, 1977.

Some chapters in “Handbook of formal language theory” (3 vols.), G. Rozenberg, A. Salomaa (eds.), Springer 1997:

• Jean-Michel Autebert, Jean Berstel, Luc Boasson, Context-free languages and push-down automata, vol. 1, ch. 3

Related entries

• formal grammar
• context-sensitive grammar
• mildly context-sensitive grammar
• pregroup grammar
• dependency grammar