nLab elasticity
Context
Cohesive -Toposes
Backround
Definition
Presentation over a site
Models
Contents
Idea
In solid state physics
In physics, specifically in solid state physics, elasticity is the tendency of solid materials to return to their original shape after being deformed.
Mathematical elasticity theory (Landau-Lifshitz 59) encodes the forces acting on a solid by a stress tensor, and the amount of deformation by a strain tensor.
One distinguishes different types of elasticity:
-
linear elasticity: here the strain tensor is related by a linear equation to the stress tensor (a generalization of Hooke's law?). To first infinitesimal order every type of material is approximately linearly elastic, the topic of infinitesimal strain theory.
-
non-linear elasticity
- hyperelasticity: exhibited by (soft) rubber
…
Analogy with a quality of space
Elasticity is commonly used as an illustration via analogy of the nature of space in physics, specifically that of manifolds and spacetimes.
In natural philosophy
In Georg Hegel‘s Encyclopedia of the Philosophical Sciences (1817) there is discussion (in the section Physik – Die Kohäsion) of the cohesion and elasticity of some substance which Hegel says is is the unity of space and time (PN§261).
In categorical logic / topos theory
William Lawvere argued that the “objective logic” of this discussion is to be formalized via categorical logic by the axiomatics of cohesive toposes (see there for references), i.e. by modal type theory equipped with shape modality and flat modality.
But Hegel goes on to speak of cohesion being refined to elasticity:
PN§297Zusatz Elasticity is the whole of cohesion.
According to PN§298 this elasticity is related to the unity of opposites that consistute Zeno's paradox of motion, hence to the modern concept of differentiation via a limit of a sequence. In terms of categorical logic this is precisely what is encoded in the infinitesimal shape modality and infinitesimal flat modality of “differential cohesion” (see there for detail).
Sticking to imagery from solid state physics, these modalities are reminiscent of concepts in infinitesimal strain theory. Notice that this applies to
structures built from relatively stiff elastic materials
Rubber-sheet geometry
These modalities above induce an axiomatization of manifolds and étale groupoids (“derived schemes”) for which a common imagery in mathematics is given by elastic rubber sheets, reflecting the fact that these spaces on top of their cohesion have a more rigid shape, namely infinitesimal shape.
In this context the topology of manifolds is often referred to as rubber-sheet geometry (e.g.Wikipedia, Britton).
Elasticity analogy of gravity
Moreover, these modalities above induce an axiomatization of Cartan geometry, hence in particular of pseudo-Riemannian geometry and hence of gravity (“general relativity”) on these manifolds.
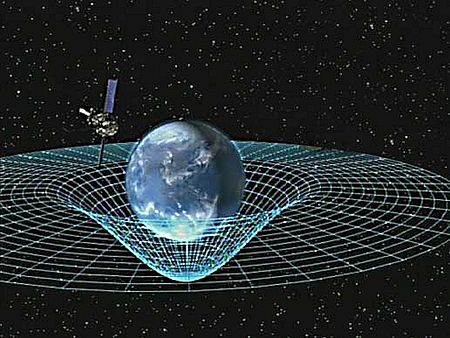
A popular imagery for that illustrates the gravitational effect of massive bodies on light by a deformation of spacetime visualizes as an elastic wire frame. This is known as the rubber-sheet analogy for gravity (e.g. Das 11, p. 69, Gabor, Volk, fig. 4 on p. 537).
This seems to go back to the technical result of (Sakharov 67), which is informally summarized in the seminal textbook (Misner-Thorne-Wheeler 73) as saying that
gravity is “an elasticity of space that arises from particle physics”
Further discussion of the analogy between the mathematical theory of elasticity and that of gravity include (Tartaglia 95,Middleton-Langston 13, Wikipedia).
In order to think of not just topology but Riemannian geometry in the above context of elasticity, the rigidity mentioned further above seems advisable. A rigidly elastic body is to be expected to produce sound when struck. This is a common imagery in Riemannian geometry, as in “hearing the shape of a drum”.
Related entries
References
In solid state physics
- Lev Landau, Evgeny Lifshitz, Theory of Elasticity, part VII of Course of Theoretical Physics, 1959, 1970
As an analogy for topology/differential geometry
- Jill Britton, Rubber sheet geometry
As an analogy for gravity
The “rubber-sheet analogy of gravity” might go back to results in
- Andrei Sakharov, Vacvuum fluctuations in curved space and the theory of gravitation, Doklady Akad. Nauk S.S.S.R. 177 70-71 (1967)
which were informally summarized in
-
Charles Misner, Kip Thorne, John Wheeler, Gravitation, 1973
-
John Wheeler, Sakharov: A man of humility, understanding and leadership, in Andrei Sakharov, Facets of a Life (GoogleBooks)
as saying that gravity is “an elasticity of space that arises from particle physics”.
The mathematical similarity between gravity and the physics of elasticity is discussed further in
-
A. Tartaglia, Four Dimensional Elasticity and General Relativity (arXiv:gr-qc/9509043)
-
Chad A. Middleton, Michael Langston, Circular orbits on a warped spandex fabric (arXiv:1312.3893, talk video)
The analogy is mentioned for expositional purpose for instance in
-
Wikipedia, Gravity well – The rubber-sheet model
-
Greg Volk, 19th Natural Philosophy Alliance Proceedings (online)
-
Ashok Das, Lectures on Gravitation, WorldScientific 2011 (publisher, GoogleBooks)
Last revised on August 4, 2015 at 13:46:15. See the history of this page for a list of all contributions to it.