nLab fusion bundle

Idea

The image of the transgression operation from bundle gerbes (with connection) to complex line bundles (with connection) on the free loop space of their base space may be characterized (Waldorf 2009, 2010, 2011) as consisting of bundles which are suitably compatible with the “fusion” of pairs of loops along thin trinions.

From Waldorf 2010

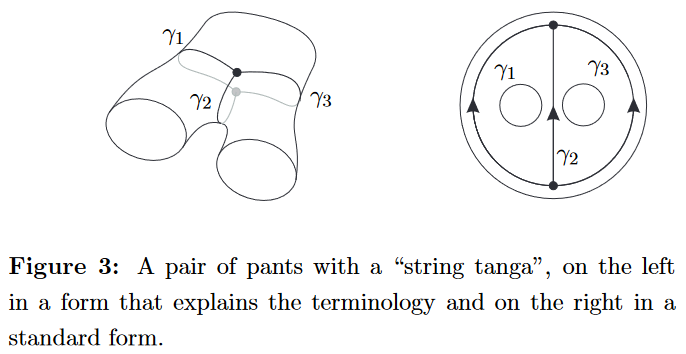
Definition

(…)

Properties

General properties

(…)

Relation to string field theory?

Curiously, the fusion operation that is formalized by the notion of fusion bundles is mathematically reminiscent of (and physically of essentially the same intuitive nature as) the “star product” on closed string fields considered in string field theory [Witten (1986),Fig. 20]:

References

• Konrad Waldorf, Transgression to Loop Spaces and its Inverse, I: Diffeological Bundles and Fusion Maps, Cah. Topol. Geom. Differ. Categ., 2012, Vol. LIII, 162-210 [arXiv:0911.3212, cahierstgdc:LIII]

• Konrad Waldorf, Transgression to Loop Spaces and its Inverse, II: Gerbes and Fusion Bundles with Connection, Asian Journal of Mathematics 20 1 (2016) 59-116 [arXiv:1004.0031, doi:10.4310/AJM.2016.v20.n1.a4]

• Konrad Waldorf, Transgression to Loop Spaces and its Inverse, III: Gerbes and Thin Fusion Bundles, Advances in Mathematics 231 (2012) 3445-3472 [arXiv:1109.0480, doi:10.1016/j.aim.2012.08.016]