nLab tangent bundle
This entry is about tangent vectors on differentiable manifolds and the bundle they form. For tangents and the tangent function see there.
Context
Differential geometry
synthetic differential geometry
Introductions
from point-set topology to differentiable manifolds
geometry of physics: coordinate systems, smooth spaces, manifolds, smooth homotopy types, supergeometry
Differentials
Tangency
The magic algebraic facts
Theorems
Axiomatics
Models
differential equations, variational calculus
Chern-Weil theory, ∞-Chern-Weil theory
Cartan geometry (super, higher)
Bundles
Context
Classes of bundles
-
vector bundle, 2-vector bundle, (∞,1)-vector bundle
real, complex/holomorphic, quaternionic
Universal bundles
Presentations
Examples
Constructions
Contents
Idea
The tangent bundle of a (sufficiently differentiable) space is a bundle over whose fiber over a point is the tangent space at that point, namely the collection of infinitesimal curves in emanating at : “tangent vectors”.
For nice enough spaces such as differentiable manifolds or more generally microlinear spaces, the tangent bundle of is a vector bundle over .
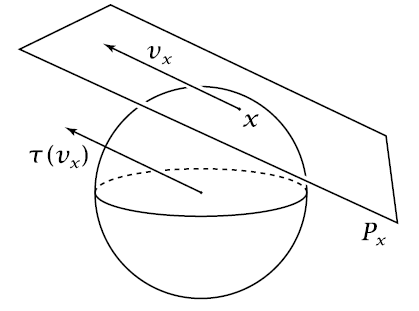
For example the graphics on the right shows the 2-sphere with one of its tangent spaces. The tangent bundle of the sphere is the union of all these tangent spaces, regarded as a topological bundle of vector space (a vector bundle) over the 2-sphere.
graphics grabbed from Hatcher
With a notion of tangent bundle comes the following terminology
-
A tangent vector on at is an element of .
-
The tangent space of at a point is the fiber of over ;.
-
A tangent vector field on is a section of .
The precise definition of tangent bundle depends on the nature of the ambient category of spaces. Below we give first the traditional definitions in ordinary differential geometry. Then we discuss the construction in more general context of smooth toposes in synthetic differential geometry and other categories of generalized smooth spaces.
Definitions
Traditional definition
We discuss the tangent bundle of a differentiable manifold by first defining tangent vectors as equivalence classes of differentiable curves in the manifold, then analyzing this construction locally over an atlas, and then gluing these local constructions together via transition functions.
Definition
(tangency relation on differentiable curves)
Let be a differentiable manifold of dimension and let be a point. On the set of smooth functions of the form
such that
define the relations
and
saying that two such functions are related precisely if either there exists a chart around such that (or else for all charts around it is true that) the first derivative of the two functions regarded via the given chart as functions , coincide at (with denoting the canonical coordinate function on ).
Lemma
(tangency is equivalence relation)
The two relations in def. are equivalence relations and they coincide.
Proof
First to see that they coincide, we need to show that if the derivatives in question coincide in one chart , that then they coincide also in any other chart .
For brevity, write
for the intersection of the two charts.
First of all, since the derivative may be computed in any open neighbourhood around , and since the differentiable functions are in particular continuous functions, we may restrict to the open neighbourhood
of and consider the derivatives of the functions
and
But then by definition of the differentiable atlas, there is the differentiable gluing function
such that
for . The chain rule now relates the derivatives of these functions as
Since is a diffeomorphism and since derivatives of diffeomorphisms are linear isomorphisms, this says that the derivative of is related to that of by a linear isomorphism , and hence
Finally, that either relation is an equivalence relation is immediate.
Definition
Let be a differentiable manifold and a point. Then a tangent vector on at is an equivalence class of the the tangency equivalence relation (def. , lemma ).
The set of all tangent vectors at is denoted .
Lemma
(real vector space structure on tangent vectors)
For a differentiable manifold of dimension and any point, let be a chart with .
Then there is induced a bijection of sets
from the -dimensional Cartesian space to the set of tangent vectors at (def. ) given by sending to the equivalence class of the following differentiable curve:
For another chart with , then the linear isomorphism relating these two identifications is the derivative
of the gluing function of the two charts at the point :
This is also called the transition function between the two local identifications of the tangent space.
If is an atlas of the differentiable manifold , then the transition functions
defined this way satisfy the following Cech cocycle conditions for all ,
-
;
-
.
Proof
The bijectivity of the map is immediate from the fact that the first derivative of at is .
The formula for the transition function now follows with the chain rule:
Similarly the Cech cocycle condition follows by the chain rule:
Definition
For a differentiable manifold and a point, then the tangent space of at is the set of tangent vectors at (def. ) regarded as a real vector space via lemma .
Example
(tangent bundle of Euclidean space)
If is itself a Euclidean space, then for any two points the tangent spaces and (def. ) are canonically identified with each other:
Using the vector space (or just affine space) structure of we may send every smooth function to the smooth function
This gives a linear bijection
and these linear bijections are compatible, in that for any three points, then
Moreover, by lemma , each tangent space is identified with itself, and this identification in turn is compatible with all the above identifications:
Therefore it makes sense to canonically identify all the tangent spaces of Euclidean space with that Euclidean space itself. As a result, the collection of all the tangent spaces of Euclidean space is naturally identified with the Cartesian product
equipped with the projection on the first factor
because then the pre-image of a singleton under this projection are canonically identified with the above tangent spaces:
This way, if we equip with the product space topology, then becomes a trivial topological vector bundle.
This is called the tangent bundle of the Euclidean space regarded as a differentiable manifold.
Remark
(chain rule is functoriality of tangent space construction on Euclidean spaces)
Consider the assignment that sends
-
every Euclidean space to its tangent bundle according to def. ;
-
every differentiable function to the function on tangent vectors (def. ) induced by postcomposition with
By the chain rule we have that the derivative of the composite curve is
and hence that under the identification of example this assignment takes to its derivative
Conversely, in the first form above the assignment manifestly respects composition (and identity functions). Viewed from the second perspective this respect for composition is once again the chain rule :
In the language of category theory this says that the assignment
is an endofunctor on the category CartSp whose
-
objects are the Euclidean spaces for ;
-
morphisms are the differentiable functions between these (for any chosen differentiability class with ).
We may now globalize the tangent bundle of Euclidean space to tangent bundles of general differentiable manifolds:
Definition
(tangent bundle of a differentiable manifold)
Let be a differentiable manifold with atlas .
Equip the set of all tangent vectors (def. ), i.e. the disjoint union of the sets of tangent vectors
with a topology by declaring a subset to be an open subset precisely if for all charts we have that its preimage under
is open in the Euclidean space with its metric topology.
Equipped with the function
this is called the tangent bundle of .
Equivalently this means that the tangent bundle is the topological vector bundle which is glued (via this example) from the transition functions from lemma :
(Notice that, by examples , each is the tangent bundle of the chart .)
The co-projection maps of this quotient topological space construction constitute an atlas
Lemma
(tangent bundle is differentiable vector bundle)
If is a -times differentiable manifold, then the total space of the tangent bundle def. is a -times differentiable manifold in that
-
The gluing functions of the atlas are -times continuously differentiable.
Moreover, the projection is a -times continuously differentiable function.
In summary this makes a differentiable vector bundle.
Proof
First to see that is Hausdorff:
Let be two distinct points. We need to produce disjoint openneighbourhoods of these points in . Since in particular are distinct, and since is Hausdorff, there exist disjoint open neighbourhoods and . Their pre-images and are disjoint open neighbourhoods of and , respectively.
Now to see that is paracompact.
Let be an open cover. We need to find a locally finite refinement. Notice that is an open map (by this example) so that is an open cover of .
Let now be an atlas for and consider the open common refinement
Since this is still an open cover of and since is paracompact, this has a locally finite refinement
Notice that for each the product topological space is paracompact (as a topological subspace of Euclidean space it is itself locally compact and second countable and since locally compact and second-countable spaces are paracompact). Therefore the cover
has a locally finite refinement
We claim now that
is a locally finite refinement of the original cover. That this is an open cover refining the original one is clear. We need to see that it is locally finite.
So let . By local finiteness of there is an open neighbourhood which intersects only finitely many of the . Then by local finiteness of , for each such the point regarded in has an open neighbourhood that intersects only finitely many of the . Hence the intersection is a finite intersection of open subsets, hence still open, and by construction it intersects still only a finite number of the .
This shows that is paracompact.
Finally the statement about the differentiability of the gluing functions and of the projections is immediate from the definitions
Proposition
(differentials of differentiable functions between differentiable manifolds)
Let and be differentiable manifolds and let be a differentiable function. Then the operation of postcomposition, which takes differentiable curves in to differentiable curves in ,
descends at each point to the tangency equivalence relation (def. , lemma ) to yield a function on sets of tangent vectors (def. ), called the differential of at
Moreover:
-
(linear dependence on the tangent vector) these differentials are linear functions with respect to the vector space structure on the tangent spaces from lemma , def. ;
-
(differentiable dependence on the base point) globally they yield a homomorphism of real differentiable vector bundles between the tangent bundles (def. , lemma ), called the global differential of
-
(chain rule) The assignment respects composition in that for , , three differentiable manifolds and for
two composable differentiable functions then their differentials satisfy
Proof
All statements are to be tested on charts of an atlas for and for . On these charts the statement reduces to that of example .
Remark
(tangent functor)
In the language of category theory the statement of prop. says that forming tangent bundles of differentiable manifolds and differentials of differentiable functions constitutes a functor
from the category Diff of differentiable manifolds to the category of differentiable real vector bundles.
Definition
Let be a differentiable manifold with differentiable tangent bundle (def. ).
A differentiable section of the tangent bundle is called a (differentiable) vector field on .
Remark
(notation for tangent vectors in a chart)
Under the bijection of lemma one often denotes the tangent vector corresponding to the the -th canonical basis vector of by
because under the identification of tangent vectors with derivations on the algebra of differentiable functions on as above then it acts as the operation of taking the th partial derivative. The general tangent vector corresponding to is then denoted by
Notice that this identification depends on the choice of chart, which is left implicit in this notation.
Sometimes, notably in texts on thermodynamics, one augments this notation to indicate the chart being used by listing the remaining coordinate functions as subscripts. For instance if two functions on a 2-dimensional manifold are used as coordinate functions for a local chart (i.e. so that and ), then one writes
for the tangent vectors and , respectively.
Via derivations of smooth functions
Remark
(derivations of smooth functions are vector fields)
Let be a smooth manifold and write for the associative algebra over the real numbers of smooth functions .
Then every smooth vector field (def. ) induces a function
by
where is a smooth curve which represents the tangent vector according to def. .
The linearity of derivatives and the product rule of differentiation imply that this function is a derivation on the algebra of smooth functions. Hence there is a function
It turns out that this function is in fact a bijection: every derivation of the algebra of smooth functions on a smooth manifold arises uniquely from a smooth tangent vector in this way.
For more on this see at derivations of smooth functions are vector fields.
Remark
For manifolds of the class , , the definition of a tangent vector as a derivation of the algebra of functions (derivations of smooth functions are vector fields) remains valid if one strengthens the definition of a derivation by adjoining, on top of the algebraic condition of the product rule
also the algebraic incarnation of the chain rule:
See Newns-Walker 56.
In synthetic differential geometry
The above definitions in ordinary differential geometry suggest the slogan
Tangent vectors are infinitesimal curves in a space.
One of the central motivations for synthetic differential geometry is the desire to provide a context in which this slogan becomes literally formally true.
Definition
(tangent bundle in smooth toposes)
Let be a smooth topos and write for the standard infinitesimal interval. For any object (any space in ), the tangent bundle of is the morphism
with
-
the internal hom of into ;
-
the evaluation map at the origin of
,
where is the hom-adjunct of .
This definition captures elegantly and usefully the notion of tangent vectors as infinitesimal curves. But it is not guaranteed that the fibers of a synthetic tangent bundle are fiberwise linear, i.e. are fiberwise -modules the way one expects. Objects for which this is true are microlinear spaces in . See there for more details.
A smooth topos is called a well-adapted model for synthetic differential geometry if there is a full and faithful embedding Diff of the category of manifolds into .
Typically, for well adapted models, under this embedding
-
manifolds are microlinear spaces
-
the synthetic definition of tangent bundle for a manifold does coincide with the ordinary notion of .
Let be the category of smooth loci. For a manifold, the exponential does exist in and is isomorphic to the ordinary tangent bundle of . (For instance MSIA, chapter II, prop 1.12.
There are well-adapted smooth topoi and presented as categories of sheaves on : the first for the Grothendieck topology where covers are finite open covers, the second where covers are finite open covers and projections (MSIA, chapter VI). Both topologies are subcanonical, hence the Yoneda embedding does preserve the above property.
Hence in these models for a manifold, its ordinary tangent bundle and the full and faithful embedding, we have isomorphisms
which respect the bundle maps.
In supergeometry
The tangent bundle of a manifold may be interpreted as a supermanifold in which has degree and the tangent vectors have degree . See shifted tangent bundle.
For other generalized smooth spaces
There are useful categories of generalized smooth spaces which are neither categories of manifolds nor smooth topoi modeling synthetic differential geometry. But most of them admit useful notions of tangent bundles, too, sometimes more than one.
See Frölicher space and diffeological space for the definitions in their context.
Related concepts
Examples of sequences of local structures
References
An early account of tangent vectors as derivations, including the -case for is in
- W. F. Newns, A. G. Walker, Tangent Planes To a Differentiable Manifold. Journal of the London Mathematical Society s1-31:4 (1956), 400–407 (doi:10.1112/jlms/s1-31.4.400)
A textbook account of tangent bundles in the context of synthetic differential geometry:
- Ieke Moerdijk, Gonzalo E. Reyes, Models for Smooth Infinitesimal Analysis Springer (1991)
Further discussion of axiomatizations in this context is in
- J.R.B. Cockett, Geoff Cruttwell, Differential structure, tangent structure, and SDG (2012) (pdf)
Discussion for diffeological spaces is in
- Carlos Torre, A tangent bundle for diffeological spaces (arXiv:math/9801046)
Last revised on August 28, 2024 at 16:37:29. See the history of this page for a list of all contributions to it.