nLab tautological line bundle
Context
Bundles
Context
Classes of bundles
-
vector bundle, 2-vector bundle, (∞,1)-vector bundle
real, complex/holomorphic, quaternionic
Universal bundles
Presentations
Examples
Constructions
Algebra
Algebraic theories
Algebras and modules
Higher algebras
-
symmetric monoidal (∞,1)-category of spectra
Model category presentations
Geometry on formal duals of algebras
Theorems
Contents
Idea
The canonical line bundle over a projective space is sometimes called its “tautological line bundle”. (For more background see also at classifying space.)
Definition
In the following, let be a star-field, possibly a skew-field
In the context of algebraic topology or differential topology, one is usually interested in being one of the three associative real normed division algebras (real numbers, complex numbers or quaternions):
equipped with their canonical conjugation operations.
The relevance of the quaternions here is the reason to insist on the generality of skew-fields and hence of some pedantry about order of products and distinction of left/right actions in the following. (For octonions the notion of tautological lines should make some sense over the first octonionic projective space but not beyond.)
Let be a natural number.
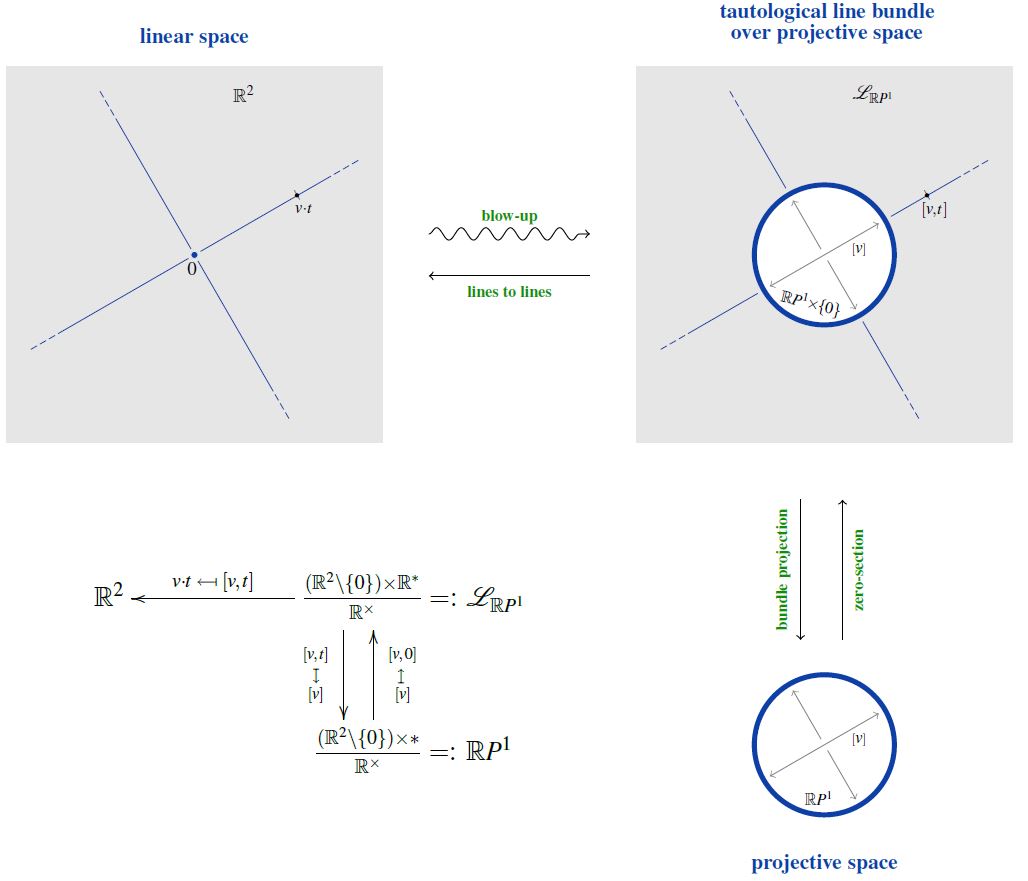
Tautological line bundle and blow-up
The tautological -line bundle over the projective space is the following vertical bundle map:
Here:
-
is the group of units of ;
-
is the canonical -dimensional -vector space,
whose elements we will also denote as lists
(2)regarded with the right -group action:
(3) -
is equipped with the right -action by inverse multiplication from the left:
(4)(equivalently, (3) and (4) are left actions of the opposite group )
-
denotes the quotient space of a product of right -spaces by their diagonal action;
-
denotes its elements as equivalence classes of elements of the original space;
-
so that, for ,
-
and hence so that the quotient construction in (1) is equivalently the -fiber associated bundle to the -principal bundle (here “” is for torsor):
For a star algebra, the quotient space (1) becomes a -vector bundle (specifically: line bundle) via the residual left action of on itself by conjugate right multiplication.
The line bundle (1) is “tautological” in the sense that its fiber over a point labeled – which may be regarded as the name of the line spanned by the vector – consists of all the points on that line – as made explicit by the horizontal map in (1).
Often the tautological line bundle is referred to via the notation “”, which in algebraic geometry is standard notation for its abelian sheaf of sections (see e.g. Wirthmüller 12, p. 14 (16 of 67)):
- “” “”
The corestriction of the horizontal map in (1) to
exhibits the total space of the tautological bundle as the “blow-up” of the origin of .
The following illustration shows the tautological real line bundle over 1-dimensional real projective space, but the general picture is “the same”, up to higher dimensionality of all spaces involved:
Dual tautological line bundle and its Thom space
The dual line bundle of the tautological line bundle (1) is
with typical fiber instead of , meaning that the action of on the fibers is now the direct right multiplication action (3), instead of the dual action (4).
Often the dual tautological line bundle is referred to via the notation “”, which in algebraic geometry is standard notation for its abelian sheaf of sections:
- “” “”.
The horizontal map in (6) embeds the complement of the single point . That point however is the limit as , hence is the image of the base point as (6) extends to a map on the Thom space of the dual tautological line bundle:
(E.g.: Tamaki & Kono 2006, Part III, Lemma 3.8, bewaring that these authors secretly identify lines with dual lines – as seen from the inner product used in the second but last line on their p. 46. Also see Conner & Floyd 1966, Part I, Prop. 4.3 for an alternative perspective in terms of coset spaces.)
Notice how the inclusion of the point at in the Thom space interplays with the condition that is excluded in the base space.
Under the canonical inclusion of projective spaces their dual tautological line bundles (6) evidently pullback to each other, and their total spaces compatibly include into each other:
Here the coordinate expressions make manifest that the induced inclusions of the Thom spaces of the tautological line bundles recover, under the identification (7), the canonical inclusion of the projective spaces:
Notice how, in this coordinatization, the projective spaces are horizontally included by adjoining a 0-coordinate to the left of the list (2) and vertically by adjoining a 0-coordinate to the right.
It follows that under forming a suitable colimit over this diagram as , in a suitable category (typically in homotopy types of topological spaces if is a topological field, see also below), the infinite projective space wants to be equivalent to the Thom space of its dual tautological line bundle:
See at zero-section into Thom space of universal line bundle is weak equivalence.
As a topological line bundle
We make fully explicit how the tautological line bundle (1) is a locally trivial topological vector bundle. Hence regard now as a topological field, either
-
the real numbers,
-
or the complex numbers
equipped with their Euclidean metric topology.
Definition
(topological projective space)
Let . Consider the Euclidean space equipped with its metric topology, let be the topological subspace which is the complement of the origin, and consider on its underlying set the equivalence relation which identifies two points if they differ by multiplication with some (necessarily non-zero):
The equivalence class is traditionally denoted
Then the projective space is the corresponding quotient topological space
Definition
(standard open cover of topological projective space)
For the standard open cover of the projective space (def. ) is
with
To see that this is an open cover:
-
This is a cover because with the orgin removed in at every point at least one of the has to be non-vanishing.
-
These subsets are open in the quotient topology , since their pre-image under the quotient co-projection coincides with the pre-image under the projection onto the th coordinate in the product topological space (where we write ).
Definition
(tautological topological line bundle)
For a topological field and , the tautological line bundle over the projective space is the topological -line bundle whose total space is the following subspace of the product space of the projective space with :
where is the -linear span of .
(The space is the space of pairs consisting of the “name” of a -line in together with an element of that -line).
This is a bundle over projective space via the projection function
Proposition
(tautological topological line bundle is well defined)
The tautological line bundle in def. is well defined in that it indeed admits a local trivialization.
Proof
We claim that there is a local trivialization over the canonical open cover from def. . This is given for by
First, this is clearly a bijection of underlying sets.
To see that this function and its inverse function are continuous, hence that this is a homeomorphism notice that this map is the extension to the quotient topological space of the analogous map
This is a polynomial function on Euclidean space and since polynomials are continuous it is continuous. Similarly, the inverse function lifts to a rational function on a subspace of Euclidean space, and since rational functions are continuous on their domain of definition, also this lift is continuous.
Therefore by the universal property of the quotient topology, also the original functions are continuous.
Examples
Möbius strip
The tautological line bundle over the 1-dimensional real projective space is the Möbius strip.
Over Riemann sphere
The basic complex line bundle on the 2-sphere is the tautological complex line bundle over the complex projective space (the Riemann sphere).
This plays a key role in topological K-theory and more generally in complex oriented cohomology theory.
Related concepts
References
Discussion with an eye towards complex-oriented cohomology theory:
-
Pierre Conner, Edwin Floyd, p. 21 (28 of 120) in: The Relation of Cobordism to K-Theories, Lecture Notes in Mathematics 28 Springer 1966 (doi:10.1007/BFb0071091, MR216511)
-
Dai Tamaki, Akira Kono, Chapter 3, Section 2 in: Generalized Cohomology, Translations of Mathematical Monographs, American Mathematical Society, 2006 (pdf, ISBN: 978-0-8218-3514-2)
Lecture notes with an eye towards topological K-theory:
- Klaus Wirthmüller, section 2 of Vector bundles and K-theory, 2012 (pdf)
See also:
- Wikipedia, Tautological bundle
Last revised on May 11, 2024 at 06:55:48. See the history of this page for a list of all contributions to it.