nLab generalized smooth space
Context
Higher geometry
higher geometry / derived geometry
Ingredients
Concepts
-
geometric little (∞,1)-toposes
-
geometric big (∞,1)-toposes
Constructions
Examples
-
derived smooth geometry
Theorems
Generalised smooth spaces
Idea
Generalised smooth spaces are, roughly speaking, generalisations of smooth manifolds. Their raison d’etre is the following
Manifolds are fantastic spaces. It’s a pity that there aren’t more of them.
Many spaces that occur in mathematics aren’t manifolds but one would like to be able to treat them as if they were manifolds; in particular, they should have some smooth structure that goes beyond mere topology. By considering examples of these spaces and by considering what specifically one would like to do with or to them, it is possible to generalise the idea of a smooth manifold to encompass the new examples whilst preserving enough structure to retain the old tools. There have been several such generalisations in recent mathematical history. A (partial) list is below.
Often the examples of spaces that one would like to consider as manifolds are formed by applying a categorical construction to ordinary manifolds; such as limits, quotients, or function spaces. This leads one to ask for the categorical properties of each of the resulting categories of generalised smooth spaces.
Another obvious question to ask is what tools and techniques can be extrapolated from smooth manifolds to generalised smooth spaces. In addition, whilst some techniques have obvious generalisations there may be some hidden twists that are not apparent on just smooth manifolds.
Examples
According to the general nonsense of space and quantity, generalized smooth spaces may be determined by sheaves on smooth test spaces, in which case we call them smooth spaces here, or by co-(pre)sheaves on test spaces, in which case we call them structured generalized spaces here.
-
-
Chen spaces (called differentiable spaces in Chen’s works).
-
-
both
The relationships between (some) of the categories can be sumarised by the following diagram of adjoint functors:
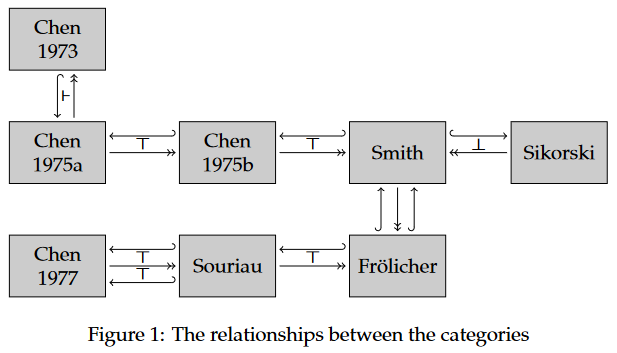
Literature
-
John Baez and Alexander Hoffnung, Convenient Categories of Smooth Spaces, Trans. Amer. Math. Soc., Vol. 363 No. 11 (2011), 5789-5825, doi:10.1090/S0002-9947-2011-05107-X, arXiv:0807.1704, blog.
-
Patrick Iglesias-Zemmour, Diffeology, Mathematical Surveys and Monographs 185, AMS (2013), publisher page, (book site).
-
Matthias Kreck, Differential Algebraic Topology: From Stratifolds to Exotic Spheres, Graduate Studies in Mathematics Volume 110, AMS (2010) (publisher page), (author pdf).
-
William Lawvere, Taking categories seriously, Reprints in Theory and Applications of Categories, No. 8 (2005) pp. 1-24 (journal).
-
David Spivak, Quasi-smooth derived manifolds, thesis (2010) (pdf).
-
Andrew Stacey, Comparative Smootheology, Theory and Applications of Categories, 25 4 (2011) 64-117, [tac:25-4), arXiv:0802.2225]
-
Martin Laubinger, Differential Geometry in Cartesian Closed Categories of Smooth Spaces (pdf)
-
Alexander Hoffnung, Smooth spaces: convenient categories for differential geometry, (pdf slides)
-
Alexander Hoffnung, From Smooth Spaces to Smooth Categories, (pdf slides)
There are also Hofer’s polyfolds.
Concerning smooth ∞-stacks there is useful material in
Remarks
Dual to generalized smooth spaces are generalized smooth algebras of functions on them, according to the general lore of space and quantity.
Further discussion
We had extensive discussion of generalized smooth spaces at the -Café:
Last revised on August 30, 2023 at 11:36:57. See the history of this page for a list of all contributions to it.