nLab subdivision
Context
Homotopy theory
homotopy theory, (∞,1)-category theory, homotopy type theory
flavors: stable, equivariant, rational, p-adic, proper, geometric, cohesive, directed…
models: topological, simplicial, localic, …
see also algebraic topology
Introductions
Definitions
Paths and cylinders
Homotopy groups
Basic facts
Theorems
Contents
Idea
Subdivision is an (often) functorial process which takes as input some combinatorial notion of space (for example, a simplicial complex or simplicial set) and produces as output a more finely meshed space. It is related to the notion of classical subdivision.
There is a more general use of the term in which one simplicial set or complex is a subdivision of another, although the relation may not be functorially generated. We will briefly look at one such example later.
There are various standard forms of functorial subdivision, the most common of which is barycentric subdivision.
Definition
For simplicial complexes
Barycentric subdivision is easiest to define for simplicial complexes. We have a pair of functors
where
-
The functor sends a simplicial complex to , regarded as a poset ordered by inclusion, and
-
The functor sends a poset to the simplicial complex whose vertex set is and whose simplices are the underlying sets of flags .
The composite is called the subdivision ; it is an endofunctor of . A vertex of is a simplex of .
There is an isomorphism , where is the usual geometric realization of simplicial complexes.
This is what it looks like for the 2-simplex.
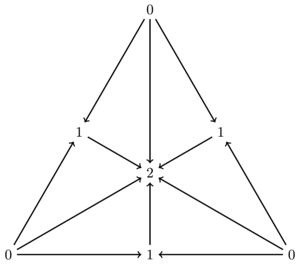
The simplicial complex which is the 2-simplex has as its poset of simplices the partially ordered set of non-empty subsets of . The subdivided simplex therefore is the flags of that poset. The diagram shows that nerve of the corresponding category, (or rather its dual), as this is the simplicial set that one gets from this. The central vertex is the whole set , the vertices on the long edges are the 2-element subsets and the three extremal vertices are the singletons.
For simplicial sets
We can now define the barycentric subdivision of a simplicial set as follows. Recall that we can make any simplicial complex into a simplicial set. If we do this for the standard -simplex, which as a simplicial complex is the set for , then we get the standard -simplex simplicial set . We can then define the subdivision of , as a simplicial set, to be the simplicial set corresponding to its simplicial-complex subdivision. Finally, we can make this functorial on maps between standard simplices, and left Kan extend to a cocontinuous endofunctor of .
Explicitly:
Definition
Write for the nerve of category of non-degenerate simplices in the standard -simplex.
For an arbitrary simplicial set, its barycentric subdivision is
A review is for instance around (Fiore-Paoli def. 3.1).
Properties
Adjointness with the -functor
By construction (or the adjoint functor theorem), the subdivision functor on simplicial sets has a right adjoint, called . A countably infinite iteration of , called , can be used to construct Kan fibrant replacements in the model structure on simplicial sets.
This functorial subdivision corresponds to the classical barycentric subdivision.
Other types of subdivision
Other classical subdivisions that are frequently encountered include the middle edge subdivision. This latter is closely related to the ordinal subdivision of simplicial sets.
Relation to category of simplices
Proposition
If every non-degenerate simplex in is given by a monomorphism , then the barycentric subdivision of def. is equivalently given by the nerve of the full subcategory of its category of simplices on the non-degenerate simplices.
References
- Rick Jardine, Simplicial approximation, Theory and Applications of Categories, Vol. 12, 2004, No. 2, pp 34-72. (web)
A review is in section 3 of
- Thomas Fiore, Simona Paoli, A Thomason model structure on the category of small -fold categories (arXiv:0808.4108)
The relation to the nerve of the category of simplices is discussed in
- R. W. Thomason, Cat as a closed model category, Cahiers Topologie Géom. Différentielle, 21(3):305–324, 1980.
Last revised on September 21, 2024 at 17:40:47. See the history of this page for a list of all contributions to it.