nLab simplicial set
Context
Combinatorics
Basic structures
- binary linear code
- chord diagram
- combinatorial design
- graph
- Latin square
- matroid
- partition
- permutation
- shuffle
- tree
- Young diagram
Generating functions
Proof techniques
Combinatorial identities
Polytopes
Homotopy theory
homotopy theory, (∞,1)-category theory, homotopy type theory
flavors: stable, equivariant, rational, p-adic, proper, geometric, cohesive, directed…
models: topological, simplicial, localic, …
see also algebraic topology
Introductions
Definitions
Paths and cylinders
Homotopy groups
Basic facts
Theorems
Content
- Idea
- Definition
- Remarks
- Examples
- The empty simplicial set
- -simplices (Yoneda embeddings)
- The minimal simplicial circle
- Cartesian products of simplices
- Simplicial complexes
- Directed graphs
- Nerve of a category
- Singular simplicial complex of a topological space
- Bar construction
- Properties
- Variants
- Related concepts
- References
Idea
Simplicial sets generalize the idea of simplicial complexes: a simplicial set is like a combinatorial space built up out of gluing abstract simplices to each other. Equivalently, it is an object equipped with a rule for how to consistently map the objects of the simplex category into it.
More concretely, a simplicial set is a collection of sets for , so that elements in are to be thought of as -simplices, equipped with a rule that says:
- which -simplices in are faces of which elements of ;
- which -simplices are thin in that they are really just -simplices regarded as degenerate -simplices.
One of the main uses of simplicial sets is as combinatorial models for the (weak) homotopy type of topological spaces. They can also be taken as models for ∞-groupoids. This is encoded in the model structure on simplicial sets. For more reasons why simplicial sets see MathOverflow here.
Definition
The quick abstract definition of a simplicial set goes as follows:
Definition
A simplicial set is a presheaf on the simplex category , that is, a functor from the opposite category of the simplex category to the category Set of sets; equivalently this a simplicial object in Set.
Equipped with the standard homomorphisms of presheaves as morphisms (namely natural transformations of the corresponding functors), simplicial sets form the category sSet (denoted both or ).
Explicitly this means the following.
Definition
(simplicial set)
A simplicial set is
-
for each injective map of totally ordered sets ()
-
for each surjective map of totally ordered sets
a function – the th degeneracy map on -simplices ( and );
such that these functions satisfy the simplicial identities.
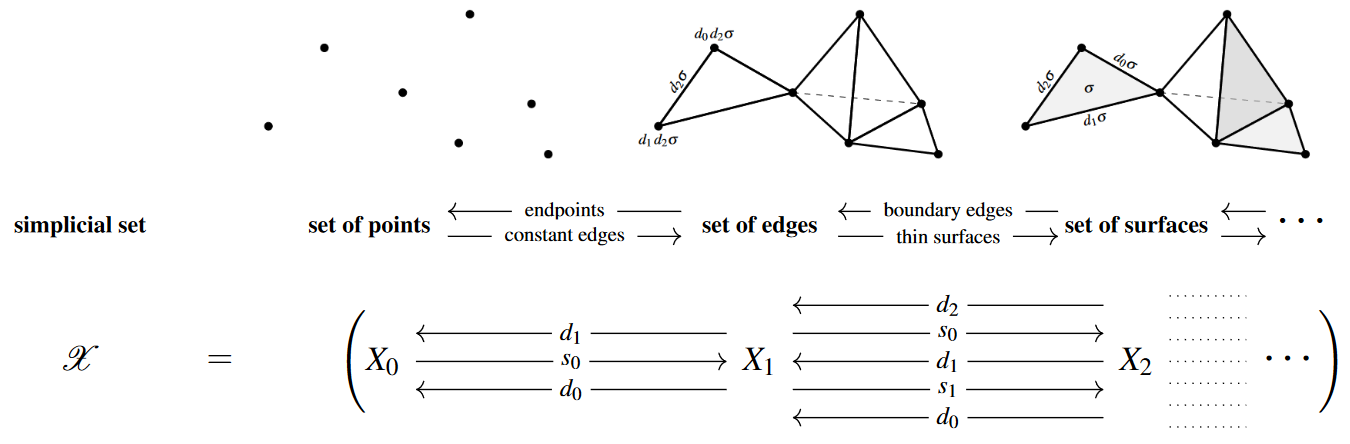
Remarks
Simplicial sets as spaces built of simplices
-
The definition is to be understood from the point of view of space and quantity: a simplicial set is a space characterized by the fact that it may be probed by mapping standard simplices into it: the set assigned by a simplicial set to the standard -simplex is the set of -simplices in this space, hence the way of mapping a standard -simplex into this space.
-
For a simplicial set, the face map
is dual to the unique injection in the category whose image omits the element .
-
Similarly, the degeneracy map
is dual to the unique surjection in such that has two elements in its preimage.
-
The maps and satisfy certain obvious relations – the simplicial identities – dual to those spelled out at simplex category.
Visualisation
(based on cubical set)
The face maps go from sets of -dimensional simplices to the corresponding set of -dimensional simplices and can be thought of as sending each simplex in the simplicial set to one of its faces, for instance for the set of 2-simplices would be sent in three different ways by three different face maps to the set of -simplices, for instance one of the face maps would send
another one would send
On the other hand, the degeneracy maps go the other way round and send sets of -simplices to sets of -simplices by regarding an -simplex as a degenerate or “thin” -simplex in the various different ways that this is possible. For instance, again for , a degeneracy map may act by sending
Notice the -labels, which indicate that the edges and faces labeled by them are “thin” in much the same way as an identity morphism is thin. They depend on lower dimensional features, (notice however that a simplicial set by itself is not equipped with any notion of composition of simplices, nor really, therefore, of identities. See quasicategory for a kind of simplicial set which does have such notions and simplicial T-complex for more on the intuitions behind this idea of “thinness”).
Examples
The empty simplicial set
The empty simplicial set is a simplicial set.
-simplices (Yoneda embeddings)
Let denote the object of the simplex category corresponding to the totally ordered set . Then the represented presheaf , typically written as is an example of a simplicial set. In particular we have and hence is a finite set with elements.
By the Yoneda lemma, the -simplices of a simplicial set are in natural bijective correspondence to maps of simplicial sets.
The minimal simplicial circle
See at minimal simplicial circle.
Cartesian products of simplices
The non-degenerate simplices in the Cartesian product of simplices
of the 1-simplex with the 2-simplex (i.e. the canonical simplicial cylinder object over the 2-simplex) is the simplicial set which looks as follows:
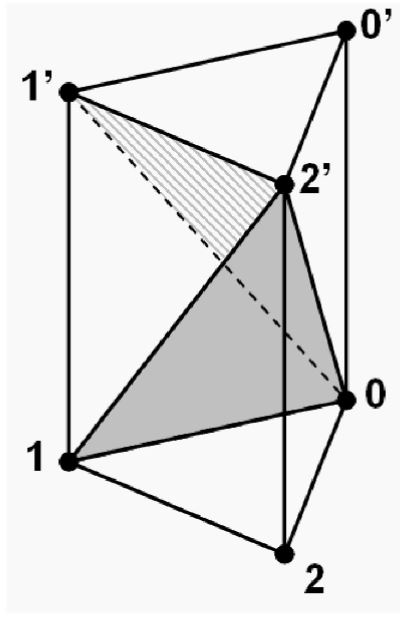
graphics grabbed from Friedman 08, p. 33
For more on this and related examples see at product of simplices.
Simplicial complexes
Every simplicial complex can be viewed a simplicial set (in several different ways).
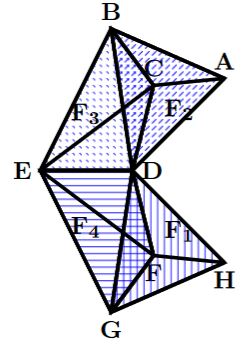
graphics grabbed form arXiv:1710.06129
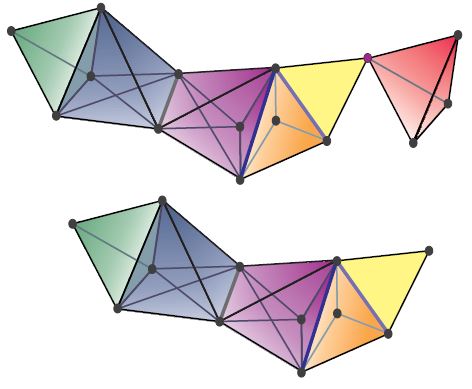
graphics grabbed from Maletic, 2013
In particular any graph is thought of as being built of vertices and edges and so is a (1-dimensional) simplicial complex. Choosing a direction on the edges then gives a directed graph and that gives a simplicial set, as follows.
Directed graphs
A directed graph (with loops and multiple edges allowed, i.e., a quiver) is essentially the same thing as a 1-dimensional simplicial set, by taking to be the set of vertices and to be the disjoint union of the set of edges with the set of vertices (the latter corresponding to the degenerate 1-simplices).
Nerve of a category
If is a small category, the nerve of is a simplicial set which we denote . If we intepret the poset defined above as a category, we define the -simplices of to be the set of functors . Equivalently, the -simplices of are the objects of , the -simplices are the morphisms, and the -simplices are strings of composable arrows in . Face maps are given by composition (or omission, in the case of and ) and degeneracy maps are given by inserting identity arrows.
Singular simplicial complex of a topological space
Recall from simplex category or geometric realization the standard functor which sends to the standard topological -simplex . This functor induces for every topological space the simplicial set
called the simplicial singular complex of . This simplicial set is always a Kan complex and may be regarded as the fundamental ∞-groupoid of .
Following up on the idea of ‘’thinness’’, a singular simplex may be called thin if it factors through a retraction to some horn of , then the well known Kan condition on can be strengthened to say that every horn in has a thin filler. This also helps to give some intuitive underpinning to the idea of thin element in this simplicial context.
Bar construction
For the moment see bar construction.
Properties
Basic properties
Proposition
(simplicial set is colimit of its elements)
Every simplicial set is the colimit of its simplices, in that
Proof
Since SimplicialSets is a category of presheaves (over the simplex category ) this is a special case of the general fact that every presheaf is a colimit of representables (this Prop., the “co-Yoneda lemma”).
Remark
In fact, the colimit in Prop. is a homotopy colimit, see there.
Classifying topos
Simplicial sets
The category of simplicial sets is a presheaf category, and so in particular a Grothendieck topos. In fact, it is the classifying topos of the theory of “intervals”, meaning totally ordered sets equipped with distinct top and bottom elements.
Specifically, if is a topos containing such an interval , then we obtain a functor sending to the subobject
The corresponding geometric realization/nerve adjunction is the geometric morphism which classifies . In particular, the generic such interval is the simplicial 1-simplex ; see generic interval for more.
The usual geometric realization into topological spaces cannot be obtained in this way precisely, since Top is not a topos. However, there are Top-like categories which are toposes, such as Johnstone's topological topos.
Cosimplicial sets
Similarly, also the category of cosimplicial sets is a classifying topos: for inhabited linear orders. See at classifying topos the section For (inhabited) linear orders.
As models in homotopy theory
(…) homotopy theory (…) Kan complex (…) quasi-category (…)
Relation to dendroidal sets
For the moment see at dendroidal set the section Relation to simplicial sets
Variants
- A symmetric set is a simplicial set equipped with additional transposition maps for . These transition maps generate an action of the symmetric group on and satisfy certain commutation relations with the face and degeneracy maps.
Related concepts
-
Segal condition, characterising the nerves of small categories
References
The original definition:
- Samuel Eilenberg, Joseph A. Zilber, Section 8 in: Semi-simplicial complexes and singular homology, Annals of Mathematics 51:3 (1950), 499–513 (jstor:1969364)
Further early discussions (aimed at simplicial homotopy theory):
-
Pierre Gabriel, Michel Zisman, Chapter II of Calculus of fractions and homotopy theory, Ergebnisse der Mathematik und ihrer Grenzgebiete 35, Springer (1967) [doi:10.1007/978-3-642-85844-4, pdf]
-
Peter May, Simplicial objects in algebraic topology, University of Chicago Press 1967 (ISBN:9780226511818, djvu, pdf)
-
Edward B. Curtis, Simplicial homotopy theory, Advances in Mathematics 6 (1971) 107–209 (doi:10.1016/0001-8708(71)90015-6, MR279808)
Exposition and introduction:
-
Greg Friedman, An elementary illustrated introduction to simplicial sets, Rocky Mountain J. Math. 42(2): 353-423 (2012) [arXiv:0809.4221, doi:10.1216/RMJ-2012-42-2-353]
-
Emily Riehl, A leisurely introduction to simplicial sets, 2008, 14 pages (pdf).
-
Francis Sergeraert, Introduction to Combinatorial Homotopy Theory, July 7, 2013, pdf.
-
Christian Rüschoff, Simplicial Sets, Lecture Notes 2017 (pdf, pdf)
Further discussion in the context of simplicial homotopy theory/algebraic topology:
-
Klaus Lamotke, Semisimpliziale algebraische Topologie, Grundlehren der mathematischen Wissenschaften 147 (1968).
-
Paul Goerss, J. F. Jardine, Chapter I of: Simplicial homotopy theory, Progress in Mathematics, Birkhäuser (1999) Modern Birkhäuser Classics (2009) (doi:10.1007/978-3-0346-0189-4, webpage)
-
Denis-Charles Cisinski, Section 2 of: Les préfaisceaux comme type d'homotopie, Astérisque, Volume 308, Soc. Math. France (2006), 392 pages (pdf)
-
André Joyal, Myles Tierney, Notes on simplicial homotopy theory, March 7, 2008, pdf.
Last revised on June 10, 2025 at 11:55:53. See the history of this page for a list of all contributions to it.