nLab Wick rotation
Context
Algebraic Quantum Field Theory
algebraic quantum field theory (perturbative, on curved spacetimes, homotopical)
Concepts
quantum mechanical system, quantum probability
interacting field quantization
Theorems
States and observables
Operator algebra
Local QFT
Perturbative QFT
Physics
physics, mathematical physics, philosophy of physics
Surveys, textbooks and lecture notes
theory (physics), model (physics)
experiment, measurement, computable physics
-
-
-
Axiomatizations
-
Tools
-
Structural phenomena
-
Types of quantum field thories
-
Contents
Idea
What is called Wick rotation (after Gian-Carlo Wick) is a method in physics for finding a construction in relativistic field theory on Minkowski spacetime or, more generally, on Lorentzian manifolds, from a related construction in Euclidean field theory on Riemannian manifolds in a way that involves or generalizes the idea of analytic continuation for the time coordinates.
The complex plane for a complexified time coordinate . After Wick rotation it is the imaginary part that replaces the “real” time .
graphics grabbed from Fulling-Ruijsenaars 87
This is motivated by the observation that the Minkowski metric (with the convention for spacetime signature) and the four-Euclidean metric are equivalent if the time components of either are allowed to have imaginary values. Hence Wick rotation, when it applies, involves analytic continuation of n-point functions to complex valued time coordinates.
For relativistic/Euclidean quantum field theory on Minkowski spacetime /Euclidean space Wick rotation is rigorously understood and takes the form of a theorem relating the Wightman axioms for n-point functions in relativistic field theory to the Osterwalder-Schrader axioms for correlators in Euclidean field theory.
See for instance Fulling-Ruijsenaars 87, section 2 for a clear account.
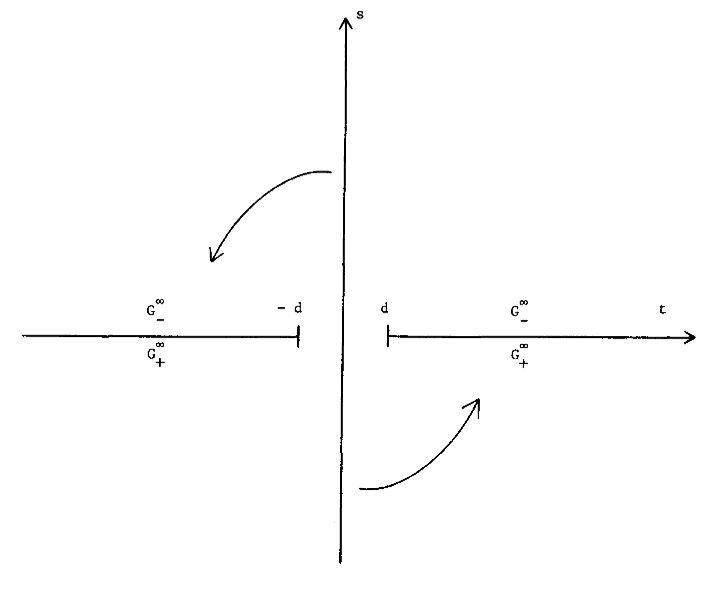
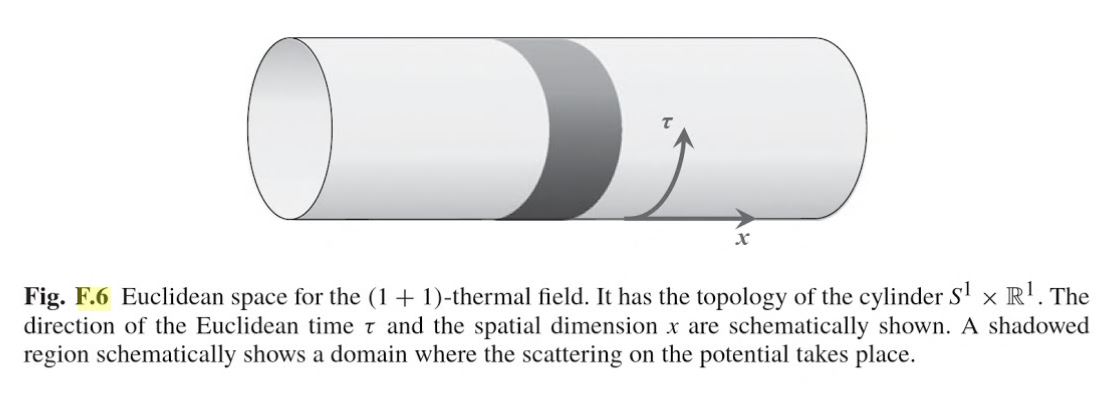
More generally, in this context Wick rotation applies to relativistic field theory in thermal equilibrium states at positive temperature (“KMS states”), and then relates this to Euclidean field theory with compact/periodic Euclidean time of length (see Fulling-Ruijsenaars 87, section 3):
In this form, Wick rotation is also known as thermal quantum field theory. See there for more.
graphics grabbed form Frolov-Zelnikov 11
Wick rotation also applies on suitable black hole-spacetimes spring thermodynamics, such as the Bekenstein-Hawking entropy, find elegant explanations, at least at the level of the manipulation of formulas (see e.g. Fulling-Ruijsenaars 87, section 4).
Example
Consider the Minkowski metric with the convention for the tensor:
and the four-dimensional Euclidean metric:
.
Notice that if , the two are equivalent.
Method
A typical method for employing Wick rotation would be to make the substitution in a problem in Minkowski space. The resulting problem is in Euclidean space and is sometimes easier to solve, after which a reverse substitution can (sometimes) be performed, yielding a solution to the original problem.
Technically, this works for any four-vector comparison between Minkowski space and Euclidean space, not just for space-time intervals.
Related concepts
References
Wick rotation between relativistic field theory in terms of Wightman axioms for n-point functions on Minkowski spacetime and Euclidean field theory in terms of Osterwalder-Schrader axioms for correlators on Euclidean space is due to
- Konrad Osterwalder, Robert Schrader, Axioms for Euclidean Green’s functions, Comm. Math. Phys. Volume 31, Number 2 (1973), 83-112 (Euclid:1103858969)
The generalization of this for positive thermal equilibrium vacuum states, relating to thermal quantum field theory with compact/periodic Euclidean time is discussed in
- Abel Klein, Lawrence Landau, Periodic Gaussian Osterwalder-Schrader positive processes and the two-sided Markov property on the circle, Pacific Journal of Mathematics, Vol. 94, No. 2, 1981 (DOI: 10.2140/pjm.1981.94.341, pdf)
The idea here apparently goes back to
- Claude Bloch, Sur la détermination de l’état fondamental d’un système de particules, Nucl. Phys. 7 (1958) 451
This has maybe first been made precise, for the case of 1+1 dimensions, in
- Raphael Høegh-Krohn, Relativistic Quantum Statistical Mechanics in two-dimensional Space-Time, Communications in Mathematical Physics 38.3 (1974): 195-224 (pdf)
Good review on the relation to thermal quantum field theory and black hole thermodynamics is in
-
S.A. Fulling, S.N.M. Ruijsenaars, Temperature, periodicity and horizons, Physics Reports Volume 152, Issue 3, August 1987, Pages 135-176 (pdf, doi:10.1016/0370-1573(87)90136-0)
-
Gary Gibbons, Malcolm J. Perry, Black Holes and Thermal Green Functions, Vol. 358, No. 1695 (1978) (jstor:79482)
New formalization in terms of complex metrics:
- Maxim Kontsevich, Graeme Segal, Wick rotation and the positivity of energy in quantum field theory, The Quarterly Journal of Mathematics 72 1-2 (2021) 673–699 [arXiv:2105.10161, doi:10.1093/qmath/haab027]
review talks:
-
Graeme Segal, Wick rotation and the positivity of energy in quantum field theory, talk at Institut des Hautes Études Scientifiques (IHÉS), June 2014 (video recording)
-
Graeme Segal, Wick Rotation and the Positivity of Energy in Quantum Field Theory, talk at IAS Physics Group Meeting, December 2021 (video recording)
Discussion of thermal Wick rotation on global anti-de Sitter spacetime (which is already periodic in real time) is in
- B. Allen, A. Folacci, Gary Gibbons, Anti-de Sitter space at finite temperature, Physics Letters B Volume 189, Issue 3, 7 May 1987, Pages 304-310 (doi:10.1016/0370-2693(87)91437-7)
See also
-
Dirk Schlingemann, From euclidean field theory to quantum field theory (arXiv:hep-th/9802035)
-
Edward Witten, The Feynman in String Theory (arXiv:1307.5124)
On the (non-)existence of Wick rotation for quantum field theory on curved spacetimes:
MathOverflow comments:
See also:
- Stefan Hollands, Robert Wald, p. 7-8 in: Quantum fields in curved spacetime, Physics Reports Volume 574, 16 April 2015, Pages 1-35 (arXiv:1401.2026, doi:10.1016/j.physrep.2015.02.001)
Last revised on November 16, 2023 at 05:04:53. See the history of this page for a list of all contributions to it.