nLab simplex
Context
Homotopy theory
homotopy theory, (∞,1)-category theory, homotopy type theory
flavors: stable, equivariant, rational, p-adic, proper, geometric, cohesive, directed…
models: topological, simplicial, localic, …
see also algebraic topology
Introductions
Definitions
Paths and cylinders
Homotopy groups
Basic facts
Theorems
Contents
Idea
The cellular simplex is one of the basic geometric shapes for higher structures. Variants of the same “shape archetype” exist in several settings, e.g., that of a simplicial set, the topological /cellular one, and categorical contexts, plus others.
Definitions
Simplicial simplices
For , the standard simplicial -simplex is the simplicial set which is represented (as a presheaf) by the object in the simplex category, so .
Cellular (simplicial) simplex
Likewise, there is a standard topological -simplex, which is (more or less by definition) the geometric realization of the standard simplicial -simplex.
Topological simplex
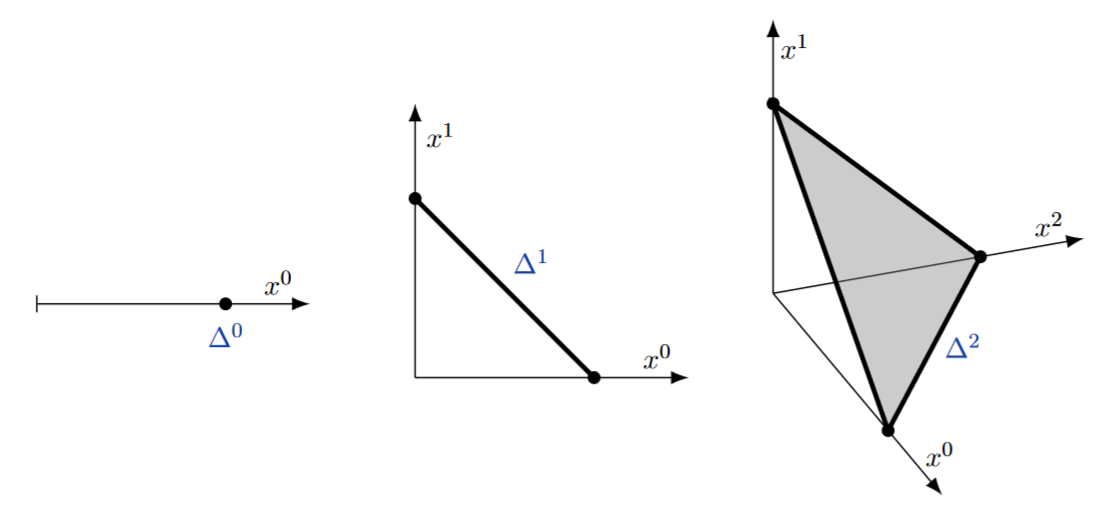
The topological -simplex is a generalization of the standard filled triangle in the plane, from dimension 2 to arbitrary dimensions. Each is homeomorphic to the closed -ball , but its defining embedding into a Cartesian space equips its boundary with its cellular decomposition into faces, generalizing the way that the triangle has three edges (which are 1-simplices) as faces, and three points (which are vertices or 0-simplices) as corners.
The topological -simplex is naturally defined as a subspace of a Cartesian space given by some relation on its canonical coordinates. There are two standard choices for such coordinate presentation, which of course define homeomorphic -simplices:
Each of these has its advantages and disadvantages, depending on application, but of course there is a simple coordinate transformation that exhibits an explicit homeomorphism between the two:
Barycentric coordinates
In the following, for we regard the Cartesian space as equipped with the canonical coordinates labeled .
Definition
For , the topological -simplex is, up to homeomorphism, the topological space whose underlying set is the subset
of the Cartesian space , and whose topology is the subspace topology inherited from the Euclidean topology on .
Definition
For , and , the th -face (inclusion) of the topological -simplex is the subspace inclusion
induced under the barycentric coordinates of def. , by the inclusion
which omits the th coordinate
Example
The inclusion
is the inclusion
of the “right” end of the standard interval. The other inclusion
is that of the “left” end .
Definition
For and the th degenerate -simplex (projection) is the surjective map
induced under the barycentric coordinates of def. under the surjection
which sends
Proposition
The collection of face inclusions, def. and degeneracy projections, def. satisfy the (dual) simplicial identities. Equivalently, they constitute the components of a functor
from the simplex category to the category Top of topological spaces. This is, up to isomorphism, the standard cosimplicial object in .
Cartesian coordinates
Definition
The standard topological -simplex is, up to homeomorphism, the subset
equipped with the subspace topology of the standard topology on the Cartesian space .
Remark
This definition identifies the topological -simplex with the space of interval maps (preserving top and bottom) into the topological interval. This point of view takes advantage of the duality between the simplex category and the category of finite intervals with distinct top and bottom. Indeed, it follows from the duality that we obtain a functor
Example
-
For this is the point, .
-
For this is the standard interval object .
-
For this is a triangle sitting in the plane like this:
Transformation between Barycentric and Cartesian coordinates
For , write now explicitly
for the topological -simplex in barycentric coordinate presentation, def. , and
for the topological -simplex in Cartesian coordinate presentation, def. .
Write
for the continuous function given in the standard coordinates by
By restriction, this induces a continuous function on the topological -simplices
Proposition
For every the function is a homeomorphism and respects the face and degeneracy maps.
Equivalently, is a natural isomorphism of functors , hence an isomorphism of cosimplicial objects
Singular simplex
Definition
For Top and , a singular -simplex in is a continuous map
Write
for the set of singular -simplices of .
As varies, this forms the singular simplicial complex of .
Properties
Relation to globes
The orientals relate simplices to globes.
Related concepts
References
- Paul Goerss, J. F. Jardine, Exp. 1.7 of: Simplicial homotopy theory, Progress in Mathematics, Birkhäuser (1999) Modern Birkhäuser Classics (2009) [doi:10.1007/978-3-0346-0189-4, webpage]
Last revised on February 5, 2024 at 16:04:24. See the history of this page for a list of all contributions to it.