nLab Globular

The initial release of Globular works best in the Chrome browser. For discussion, go to the nForum thread.

Globular may have been superceded by its successor tool homotopy.io, see there for more.

Introduction

Overview

Globular is a web-based proof assistant for finitely-presented semistrict globular higher categories (“associative $n$-categories”). It allows one to formalize higher-categorical proofs in finitely-presented n-categories, visualize them as string diagrams, and share them with collaborators, or with the world. It is available at this address:

• http://globular.science

We recommend the Chrome browser.

Globular currently operates up to the level of 4-categories. By the yoga of k-tuply monoidal n-categories, this also allows one to construct proofs in the following settings:

• Monoidal 3-category
• Monoidal 2-category, optionally with a braiding
• Monoidal category, optionally with a braiding or symmetry

The model of semistrict higher categories that Globular uses puts all the weak structure in the interchangers, and higher associated structures. At the level of 3-categories, Globular implements the axioms of a Gray category; since every tricategory is known to be equivalent to a semistrict 3-category, this means that any algebraic proof in a finitely-presented tricategory can be formalized. At the level of 4-categories, this is an implementation of a new definition of semistrict 4-category which is not yet published, and for which it is conjectured that every weak 4-category is equivalent to a semistrict 4-category.

Globular is free to use, and open-source. There is a lot to be done, on both a theoretical and practical level, and anybody can get involved with development. If you are interested, please get in touch with Jamie Vicary. Globular has been developed in the Quantum Group of the Department of Computer Science at the University of Oxford, by Krzysztof Bar, Katherine Casey, Aleks Kissinger, Jamie Vicary and Caspar Wylie.

If you’ve never used Globular before, the tutorial video is a good place to start. To report a bug, please use the issue tracker.

We are extremely grateful to John Baez, Manuel Bärenz, Bruce Bartlett, Eugenia Cheng, Chris Douglas, Eric Finster, Nick Gurski, André Henriques, Samuel Mimram and Dominic Verdon for useful discussions.

If you would like to cite Globular, you can use the BiBTeX entry

  @InProceedings{
  globular, 
  author={Krzysztof Bar and Aleks Kissinger and Jamie Vicary}, 
  title={Globular: an online proof assistant for higher-dimensional rewriting}, 
  note={\href{http://ncatlab.org/nlab/show/Globular}{ncatlab.org/nlab/show/Globular}}, 
  pages={34:1--34:11}, 
  volume=52, 
  year=2016, 
  booktitle={Leibniz International Proceedings in Informatics}}

Example proofs

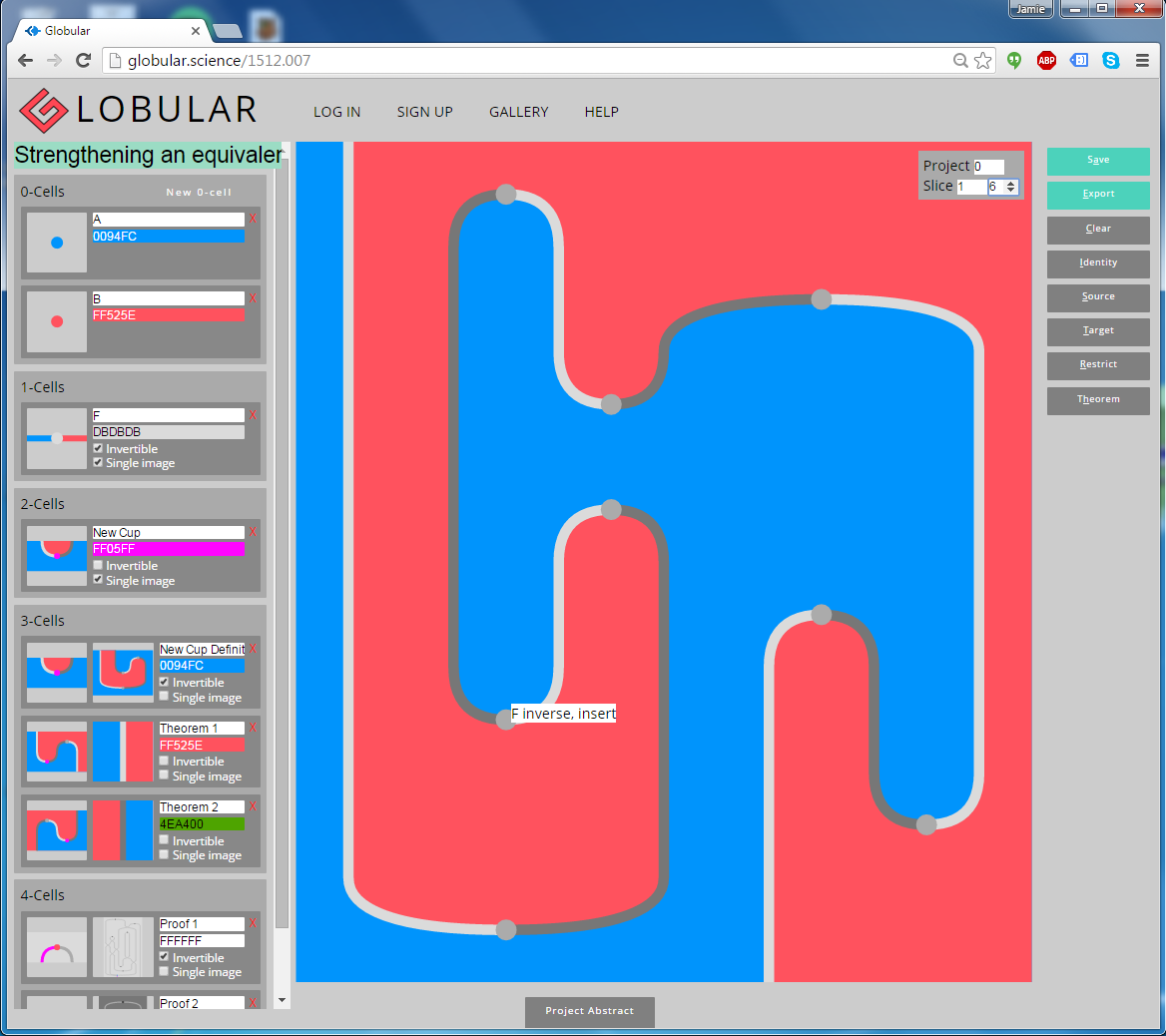
To see what can be done with Globular, look at these example proofs. To navigate through them, use the Project and Slice controls in the top-right of the main diagram (see Changing the view.)

• Frobenius implies associative (globular.science/1512.004). In a monoidal category, if multiplication and comultiplication morphisms are unital, counital and Frobenius, then they are associative and coassociative.
• Strengthening an equivalence (globular.science/1512.007). In a 2-category, an equivalence gives rise to an adjoint equivalence, satisfying the snake equations.
• Pentagon and triangle implies $\lambda_I = \rho_I$ (globular.science/1512.002). In a monoidal 2-category, if a pseudomonoid object satisfies pentagon and triangle equations, then it satisfies $\lambda_I = \rho_I$.
• The antipode is an algebra homomorphism (globular.science/1512.011). For a Hopf algebra structure in a braided monoidal category, the antipode is an algebra anti-homomorphism. (Thanks to Dominic Verdon for formalizing this.)
• The Perko knots are isotopic (globular.science/1512.012). The Perko knots are a pair of 10-crossing knots stated by Little in 1899 to be distinct, but proven by Perko in 1974 to be isotopic. Here we give the isotopy proof. A nice feature is that the second and third Reidemeister moves do not have to be entered, since they are already implied by the 3-category axioms.
• The pants bordism is commutative (globular.science/1601.005). For an oriented dualizable object in a monoidal 2-category, the associated pants bordism is commutative. (Based on unpublished notes by Scott Carter.)
• K=P#P (globular.science/1605.003). As knotted spheres in 4 dimensions, the Klein bottle is isotopic to the connect sum of two cross caps. (Based on the movie move proof in Section 2.3 of Knotted Surfaces and their Diagrams by Scott Carter and Masahico Saito.)
• The 1-twist spun trefoil is unknotted. (globular.science/1607.003). For every classical (1,1)-knot, the knotted surface in $\mathbb{R}^4$ given by its 1-twist spin is unknotted. Here we give the explicit unknotting isotopy for the trefoil. (Based on the movie move proof in Carter and Saito. Formalization by Scott Carter.)
• Swallowtail coherence (globular.science/1512.006). In a 3-category, an adjunction of 1-morphisms gives rise to a coherent adjunction satisfying the swallowtail equations.
• Butterfly coherence (globular.science/1605.002). In a 4-category, an adjunction of 1-morphisms gives rise to a coherent adjunction satisfying the butterfly equations. (Developed by Krzysztof Bar and Jamie Vicary.)
• Kirby calculus and 4-manifolds (globular.science/1808.001). It’s well-known that the braid groups are 3-endomorphism spaces in the free 3-category over a single object and a single (nontrivial) 2-morphism. In Kirby calculus (using the “dotted circle convention” by Akbulut), smooth 4-manifolds are specified by links. By adding a few more generators and relations (for handle slides and handle cancellations, a.k.a. Kirby moves), Kirby diagrams are the endomorphisms of the 2-identity in the previously mentioned 3-category. Some example manifolds are defined and some example diffeomorphisms are formalised. (By Manuel Bärenz)

Basic functionality

Overview

Signatures and diagrams. Using Globular involves two main techniques: building the signature, and building a diagram over the signature. The signature is the list of cells that are available, and the diagram is a particular composite of those cells. A diagram can be thought of as a composite cell in the free semistrict $\infty$-category generated by the signature.

The signature can be enlarged by building diagrams $S$ and $T$, and assigning them in turn as the source and target of a new cell, using the ‘Source’ and ‘Target’ buttons in the menu on the right of the interface. Any pair of diagrams can be chosen which satisfy the globularity conditions $s(S) = s(T)$ and $t(S) = t(T)$. The new cell can then be given a name and a colour, to make it easy to identify.

Diagrams are built by clicking on cells of the signature, and by clicking and dragging on the diagram itself. Signature cells of dimension $n+1$ act on $n$-diagrams by rewriting, replacing a subdiagram of shape $S$ and replacing it with a subdiagram of shape $T$.

The only things that Globular understands are $k$-cells, for some value of $k$. So if you want to build an $n$-category where an equation $f=g$ holds between $n$-cells, you have to do it by adding $(n+1)$-cells $a:f \to g$ and $b:g \to f$. If you then build some composite $C[f]$ involving $f$, you can apply the cell $a$ to obtain $C[g]$, and we interpret this as the equation $C[f]=C[g]$. In a slogan, this is equality via rewriting. This is consistent with the basic premise of homotopy type theory: treat your proofs as first-order structures, which can themselves be reasoned about directly.

Accounts. If you create an account on the site, you can save workspaces to your private account, and resume work on them when you log back in to your account from any computer. You can also click ‘Share’, which shares a workspace privately with another user, and ‘Publish’, which creates a permanent public version of your workspace that can be linked to from a research paper, or from elsewhere on the web.

Export and import. Use the ‘Export’ feature to download a copy of your workspace to your local machine, and ‘Import’ to upload a previously-download workspace. This functionality only involves your browser, not the globular.science server, so you do not need to log in or even create an account to use these features. If you import a workspace, log in, and click ‘Save’, then a copy of the imported workspace will be saved to the server.

Security and privacy. The plain text of your password is not stored on the server. However, your private workspaces are saved in plain text, and as such should not be considered highly secure, as they could be accessed by someone with site administrator credentials. The administrators pledge not to access any user data, except from the registered email address, without the permission of that individual user. In other words: your private work is private! User data is backed up nightly to a secure server.

Manipulating diagrams

A diagram is a composite of the cells in the current signature, and basic diagram manipulation can be performed by clicking on the signature, as follows, where we suppose our diagram $D$ is $k$-dimensional.

• Creation. If the current diagram is empty, clicking the icon of a cell in the signature constructs a diagram which consists solely of the selected generator.
• Rewriting. Selecting a $(k+1)$-cell $G$ from the signature displays a list of all the ways that its source $s(G)$ can be identified as a subdiagram of $D$. Choosing element of this list will then modify $D$, deleting the part of it which was chosen as matching the source $s(G)$, and replacing it with the target $t(G)$.
• Attaching. Selecting a $p$-cell $G$ for $p \leq k$ displays a list of all the ways that $G$ can be attached to $D$ along one of its boundaries. Choosing an element of this list performs the attachment.

The menu on the right-hand side of the screen gives further commands. Each of these commands has a shortcut key, which is also given.

• Clear c. Deletes the current diagram.
• Identity i. Builds the identity $(k+1)$-diagram on the current $k$-diagram.
• Source s. Saves the current diagram as the source of a new generator.
• Target t. Saves the current diagram as the target of a new generator.
• Restrict r. Replaces the current diagram with the subdiagram currently being viewed (see Changing the view.)
• Theorem h. Creates a new theorem witnessing the current diagram (see Invertibility.)
• Graphic g. Downloads a PNG representation of the current diagram.

Also, the user can click and click-and-drag on the diagram to produce various effects. When a command is ambiguous, a menu will be presented to allow the user to choose their preferred action.

• Click. This attempts to attach or rewrite, as appropriate for the location of the click, with an element of the signature. If an element of the signature is marked as invertible, then the higher structure this implies will also be considered for attachment.
• Click-and-drag. This attempts to attach or rewrite using an interchanger, or naturality for the interchanger, or invertibility of some cell. This is sensitive to both the click location and the direction of the drag, in a way which should be intuitive. This also allows cells to be cancelled from the top or bottom of a diagram.

Clicking and dragging is designed to work as if you were really ‘touching’ the strings. So if you want to braid one strand over another, click the strand to ‘grab’ it, and ‘pull’ it to one side. If you want to pull a vertex through a braiding, click the vertex to ‘grab’ it, and ‘pull’ it up or down through its adjacent braiding. Of course, Globular will only carry out the command if the move you are attempting to make is actually valid in that location.

The most common move to perform is a basic interchanger, where two unrelated critical points with adjacent heights have their heights exchanged. Holding the Shift button while clicking-and-dragging tells Globular to only look for basic interchanger moves. This speeds up the processing, and is particularly useful for applying long chains of interchangers.

In order to undo any change then click the back button in your browser. This feels very counter-intuitive but trust me it works!

Changing the view

Globular can currently present string-diagram visualizations of 0-, 1- and 2-dimensional diagrams. Viewing a $k$-dimensional diagram for $k \gt 2$ is made possible by projection and slicing, controlled by number scrollers which appear in the top-right of a diagram.

• Project. This determines the number of dimensions to be projected; it can take any value $p$ in the range $0 \leq p \leq k$. Projecting a dimension causes it to be effectively ignored by Globular; it is as if you are looking at a shadow of the true image. The resulting diagrams are exactly the singularity graphics which are a common tool in higher Morse theory.
• Slice. Having decided to project out $p$ dimensions, and supposing the image being displayed is $v$-dimensional (for $v \in \{0,1,2\}$), that leaves $k - p - v$ dimensions still to be handled. If this sum is positive, coordinates must be chosen using the slice controls to position the view within an appropriate $v$-dimensional subdiagram.

You can also zoom the main diagram using the scroll wheel of your mouse, and scroll around by clicking-and-dragging with the right mouse button (on a Mac trackpad, this is a two-fingered press-hard-and-drag. Yes, this really is a thing. If it doesn’t seem to work, you’re not pressing hard enough—the trackpad should ‘click’ under your fingers.)

Technical implementation details

Globular is written in Javascript, and performs all its computations client-side, in the browser. Most of the computations it has to perform are linear in the size of the diagram, so this is quite computationally feasible, even for large proofs. The back-end is a Node.js server that allows the saving, sharing and publishing of workspaces. Graphics are implemented in SVG. Project data is compressed using the LZ4 algorithm.

Singularities

Overview

In a 2-category, a 1-cell and a 2-cell can be composed in one direction (horizontal composition), and two 2-cell can be composed in two directions (horizontal and vertical composition.) In general, in a traditional globular $n$-category, a $p$-cell and an $q$-cell can be composed in $\text{min}(p,q)$ different directions: along a common boundary 0-cell, or 1-cell, and so on, up to a common boundary $(\text{min}(p,q)-1)$-cell.

In Globular, composition works differently: a $p$-cell and a $q$-cell can be composed in just one way: along a common boundary $(\text{min}(p,q)-1)$-cell. The reason for this design decision is that in terms of the graphical calculus, of all the different composites that an ordinary globular $n$-category allows, this is the only composition that results in a diagram in generic position. Nothing is lost by this restriction, since (conjecturally) the other composites can be recovered up to isomorphism by whiskering, in just the same way that horizontal composition of 2-cells in a 2-category can be expressed in terms of vertical composites and whiskering of 2-cell by identity 1-cell.

For every way that Globular doesn’t let you compose cells—that is, for every $p,q$ and every $0 \leq n \lt \text{min}(p,q)$—there exists a $(p+q-n-1)$-cell, which resolves the singularity that would be created if this composite were actually formed. These singularity resolutions manifest in Globular as higher-dimensional cells, which allow parts of a diagram to move around each other; using them effectively is a key part of formalizing higher-dimensional proofs. The main difficulty in the definition of semistrict $n$-categories is describing these structures.

In this section we list the singularities which Globular recognizes. We organize them by categorical dimension, because to formalize a proof in an $n$-category, you may need to make use of every type of $k$-category singularity for $k \leq n$. Also, you can add any fixed natural number to the dimensions involved to get higher-dimensional versions of the same singularities; for example, interchangers arise as the composite of two $n$-cells along a common boundary $(n-2)$-cell.

2-category singularities

Interchangers

• Composite: two $2$-cells composed along a common boundary 0-cell, forming a 3-cell resolution.
• Interface: When unprojected, click the vertex to be interchanged and drag it up or down; if the interchanger is ambiguous because the source or target is the identity, then make your drag slightly to the left or right. When projected, grab the wire to be interchanged, and drag in the desired direction.

$\mathraisebox{1.8cm}{\to}$ $\qquad\qquad$

3-category singularities

Naturality of the interchanger in one variable

• Composite: a $2$-cell and a $3$-cell composed along a common boundary 0-cell, forming a 4-cell resolution.
• Interface: …

4-category singularities

Naturality of naturality of the interchanger in one variable

• Composite: a 2-cell and a 4-cell composed along a common boundary 0-cell, forming a 5-cell resolution.
• Interface: …

Naturality of the interchanger in two variables

• Composite: two 3-cells composed along a common boundary 0-cell, forming a 5-cell resolution.
• Interface: …

Naturality of invertibility of the interchanger

• Composite: …
• Interface: …

Contractible 3rd Reidemeisterators

• Composite: …
• Interface: …

Other features

Invertibility

A $k$-cell $f:A \to B$ in an $\infty$-category is invertible when there is an inverse cell $f ^{-1} : B \to A$, and invertible $(k+1)$-cells $\mu: \mathrm{id}_A \to f ^{-1} \circ f$ and $\nu: \mathrm{id}_B \to f \circ f ^{-1}$. This is a co-inductive definition, giving rise to an infinite amount of higher-dimensional structure.

In Globular, selecting the ‘Invertible’ option for a cell in the signature allows this higher structure to be used in diagrams, by clicking or clicking-and-dragging at a point of a diagram or its boundary. If more than one piece of higher invertible structure could be inserted at the location of the click, a menu is presented and the user can choose which is intended.

Popup labels

When you move your pointer over a diagram, a little label will pop up telling you what’s underneath the pointer. Doing this near a vertex, you will see that Globular isn’t really aware that the lines curve, so you will need to take care when clicking or clicking-and-dragging that Globular is correctly identifying the structure you are trying to interact with.

The labels are written using the following syntax, where ‘X’ is some arbitrary label denoting a $k$-cell, and where ‘.’ is forward composition of $k$-cells. Note that every comma increases the dimension by 1.

• ‘X inverse’ describes the $k$-cell which is the inverse of $X$
• ‘X, insert’ describes the canonical $(k+1)$-cell of type $\text{id} _{s(X)} \to X . X^{-1}$
• ‘X, cancel’ describes the canonical $(k+1)$-cell of type $X . X^{-1} \to \text{id} _{s(X)}$
• ‘Interchanger’ describes the height-exchange cell
• ‘Pull-through interchanger above’, ‘Pull-through interchanger underneath’, ‘Pull-through inverse interchanger above’ and ‘Pull-through inverse interchanger underneath’ describe the 4 different ways that a cell can be pulled through an interchanger

Note that interchangers are of dimension at least 3, and pull-throughs are of dimension at least 4.

Theorems

The theorem command allows a diagram to be stored, in a such way that it can be reused as a component in subsequent diagrams. The idea is that the diagram is a ‘theorem’ proving that its source can be rewritten into its target. The ‘proof’ is the diagram itself.

Concretely, let $D$ be the current diagram, which is $k$-dimensional, and let $s(D)$ and $t(D)$ be its source and target $(k-1)$-diagrams. Then the theorem command command creates two new generators:

• A $k$-generator $T$ with source $s(D)$ and target $t(D)$
• An invertible $(k+1)$-generator $P$ with source $T$ and with target $D$

The generator $T$ can be used in future proofs to ‘stand in’ for the diagram $D$. At any point, the generator $P$ can be used to replace $T$ with the content of diagram $D$. Since $P$ is invertible, it could also be used to identify $D$ as a subdiagram of a larger proof, and replace it with $T$, making the larger proof easier to understand.

Coordinates

Composites produced by Globular are in generic position; for example, no two vertices ever appear at the same height. As a result, there is a simple coordinate system that can be used to refer to elements of a diagram. For a $k$-dimensional cell in an $n$-dimensional diagram, $(n-k+1)$ coordinates must be provided; that is, the number of coordinates is the codimension of the cell, plus 1. Moving the mouse cursor over a diagram in the screen shows the coordinate of the element underneath the cursor.

The coordinate system for an $n$-diagram is defined in the following way. An $n$-cell at height $y$ has coordinate $[y]$. A $k$-cell for $k \lt n$ has leading coordinate given by its height $z$ in the diagram, and subsequent coordinates given by its coordinates in the slice diagram at that height.

Related entries

• homotopy.io

• rewriting

proof assistants:

based on plain type theory/set theory:

• Metamath

• Mizar, NuPRL, Isabelle, HOL

based on dependent type theory/homotopy type theory:

• Coq, Agda, Lean, Arend

based on cubical type theory:

• cubicaltt

• redtt

• yacctt

• RedPRL

• Cubical Agda

  • library and demos

  • 1lab (cross-linked reference resource)

based on modal type theory:

• Agda-flat: installation instructions

based on simplicial type theory:

• Rzk

For monoidal category theory:

• DisCoPy

For higher category theory:

• opetopic type theory

• Globular, homotopy.io

projects for formalization of mathematics with proof assistants:

• Archive of Formal Proofs (using Isabelle)

• ForMath project (using Coq)

• MathScheme

• UniMath project (using Coq and Agda)

• Xena project (using Lean)

Other proof assistants

• Andromeda

Historical projects that died out:

• The QED Project

References

• Krzysztof Bar, Aleks Kissinger, Jamie Vicary, Globular: an online proof assistant for higher-dimensional rewriting, Logical Methods in Computer Science 14 1 (2018) [doi:10.23638/LMCS-14(1:8)20182018), arXiv:1612.01093]

• Jamie Vicary, Globular tutorial video, 2015-12-07 15 minute video

• Jamie Vicary, Data Structures for Quasistrict Higher Categories, referencing arxiv:1610098, 2016-12-05 talk at Simons Institute 48 minute video

category: software