nLab Starobinsky model of cosmic inflation

Idea

In phenomenology of cosmology, the Starobinsky model of cosmic inflation takes into account – and takes as the very source of the inflaton field – higher curvature corrections to the Einstein-Hilbert action of gravity, notably the term $R^2$ (square of the Ricci curvature).

The Starobinsky model stands out among models of inflation as predicting a low value of the scalar-to-tensor ratio $r$, specifically it predicts

$$r \sim \frac{12}{N^2}$$

where $N$ is the number of $e$-foldings during inflation (see e.g. Kehagias-Dizgah-Riotto 13 (2.6)).

Observational support

Models of Starobinsky-type are favored by experimental results (PlanckCollaboration 13, BICEP2-Keck-Planck 15, PlanckCollaboration 15, BICEP3-Keck 18) which give a low upper bound on $r$, well below $0.1$ (whereas other models like chaotic inflation are disfavored by these values), see (PlanckCollaboration 13, page 12).

With respect to this data, the Starobinsky model (or “$R^2$ inflation”) is the model with the highest Bayesian evidence (Rachen, Feb 15, PlanckCollaboration 15XX, table 6 on p. 18) as it is right in the center of the likelihood peak, shown in dark blue in the following plots (PlanckCollaboration 13, figure 1, also Linde 14, figure 5) and at the same time has the lowest number of free parameters :

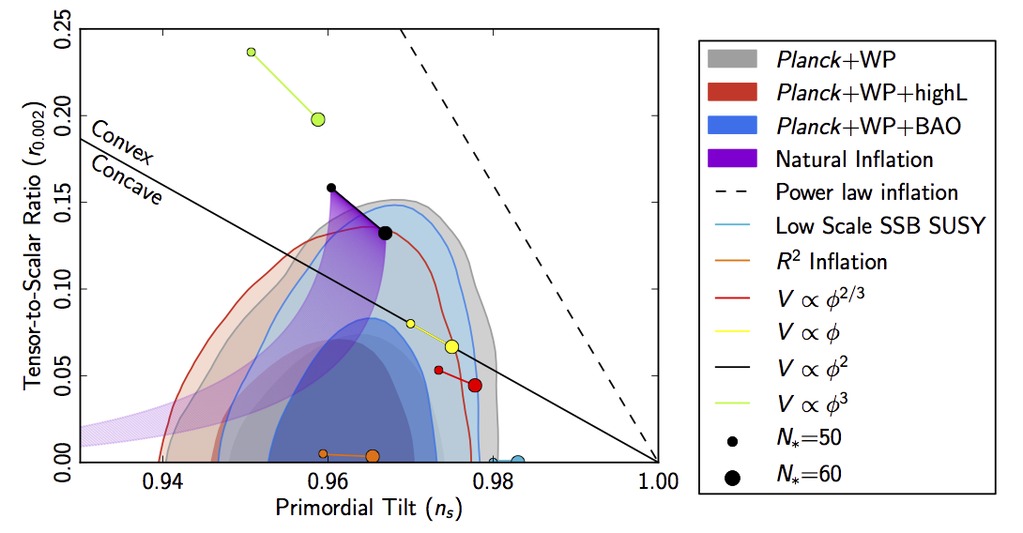
This remains true with the data of (PlanckCollaboration 15), see (PlanckCollaboration 15 XIII, figure 22) and in the final analysis (PlanckCollaboration 18X, Fig 8), which gives the following (from here):

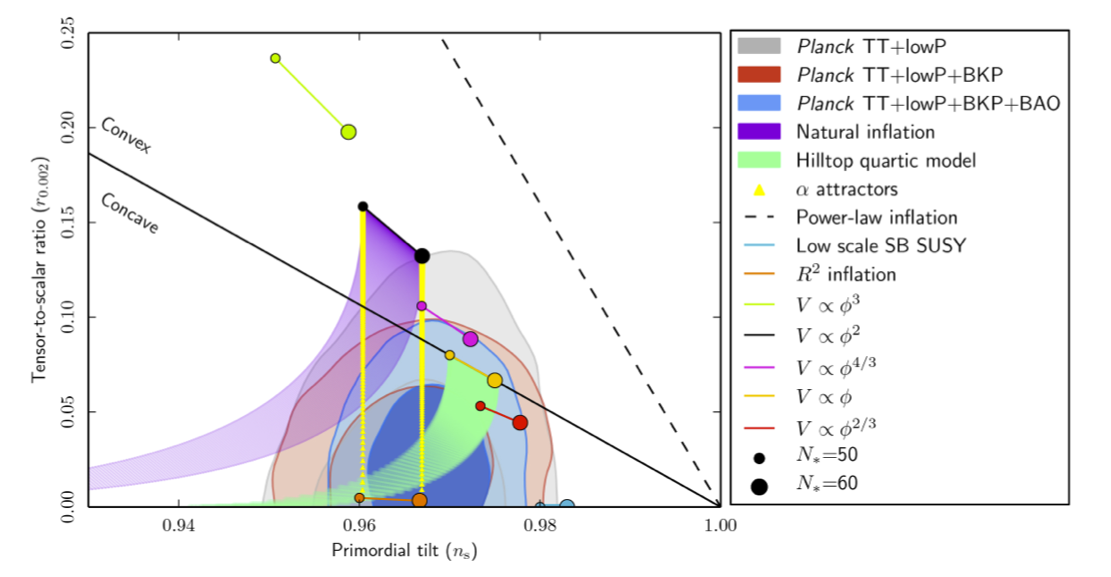
$R^2$ inflation has the strongest evidence among the models considered here. However, care must be taken not to overinterpret small differences in likelihood lacking statistical significance. The models closest to $R^2$ in terms of evidence are brane inflation and exponential inflation, which have one more parameter than $R^2$ (PlanckCollaboration 15XX, p. 18)

This picture is further confirmed by observations of the BICEP/Keck collaboration reported in BICEP-Keck 2021, whose additional data singles out the dark blue area in the following (Fig. 5):

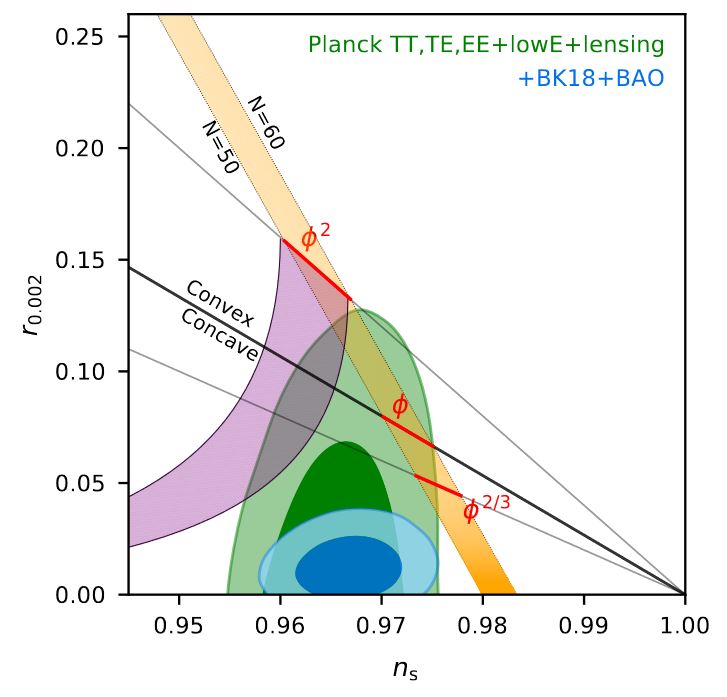
See also Ellis 13, Ketov 13, Efstathiou 2019, 50:49 for brief survey of Starobinsky inflation in relation to observation, and see Kehagias-Dizgah-Riotto 13 for more details. There it is argued that the other types of inflationary models which also reasonably fit the data are actually equivalent to the Starobinsky model during inflation.

Embedding into supergravity

Being concerned with pure gravity (the inflaton not being an extra matter field but part of the field of gravity) the Starobinsky model lends itself to embedding into supergravity (originally due to Cecotti 87, see e.g. Farakos-Kehagias-Riotto 13). Such embedding has been argued to improve the model further (highlighted e.g. in Ellis 13), for instance by

• shrinking the necessary initial homogeneous patch from $\sim 10^3$ Planck lengths (which would be in need of further explanation) down to just $\sim 10^1$ Planck lengths (Dalianis-Farakos 15 equations (68), (72) in v1, equations (4.11), (4.17) in v3, reviewed in Dalianis 16);

• naturally subsuming a mechanism for supersymmetry breaking (Ferrar-Kehagias 14, DFKRU 14) notably with a Starobisnky potential naturally induced from gravitino condensation (Alexandre-Houston-Mavromatos 14).

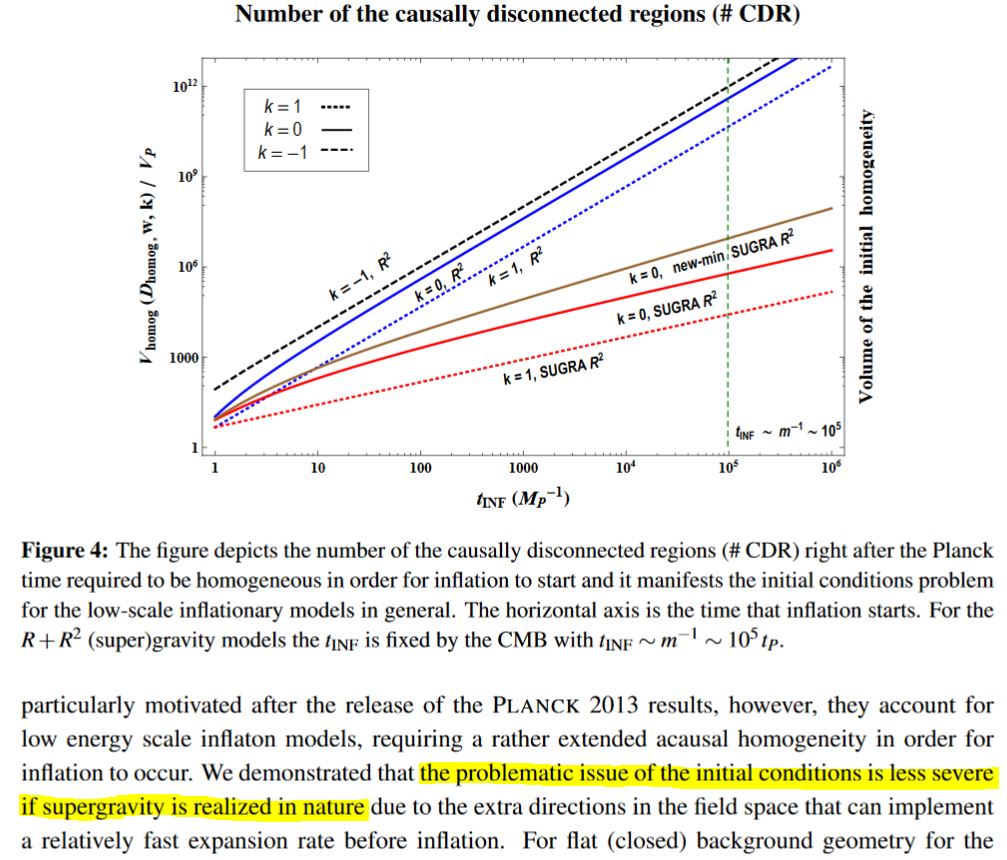
graphics grabbed from Dalianis 16, p. 8

More concretely, in Hiraga-Hyakutake 18 a simple model of 11-dimensional supergravity with its $R^4$ higher curvature correction (see there) is considered and claimed to yield inflation with “graceful exit” and dynamical KK-compactification:

graphics from Hiraga-Hyakutake 18, p. 8

References

General

The model is due to

• Aleksei Starobinsky, A new type of isotropic cosmological models without singularity, Phys. Lett. B 91 (1980) 99-102 [doi:10.1016/0370-2693(80)90670-X]

and the analysis of its predictions is due to:

• Viatcheslav Mukhanov and G. V. Chibisov, JETP Lett. 33 (1981) 532 and: Pisma Zh. Eksp. Teor. Fiz. 33 (1981) 549 [spire:170051]

• Aleksei Starobinsky, Isotropization of arbitrary cosmological expansion given an effective cosmological constant, JETP Lett. 37 (1983) 66-69 [spire:187801]

• Aleksei Starobinsky, The Perturbation Spectrum Evolving from a Nonsingular Initially De-Sitter Cosmology and the Microwave Background Anisotropy, Sov. Astron. Lett. 9 (1983) 302 [spire:199078]

The experimental data supporting the model is due to

• Planck Collaboration, Planck 2013 results. XXII. Constraints on inflation (arXiv:1303.5082)

• Planck Collaboration, BICEP2 A Joint Analysis of BICEP2/Keck Array and Planck Data (arXiv:1502.00612)

• Planck Collaboration, Planck 2015, Overview of results (arXiv:1502.01582)

• Planck Collaboration, Planck 2015 results. XIII. Cosmological parameters (arXiv:1502.01589)

• Planck Collaboration, Planck 2015 results. XX. Constraints on inflation (arXiv:1502.02114)

• Planck Collaboration, Planck 2018 results. X. Constraints on inflation (arXiv:1807.06211)

• BICEP/Keck Collaboration: BICEP / Keck XIII: Improved Constraints on Primordial Gravitational Waves using Planck, WMAP, and BICEP/Keck Observations through the 2018 Observing Season, Phys. Rev. Lett. 127, 151301 (arXiv:2110.00483, doi:10.1103/PhysRevLett.127.151301)

See also

• Debika Chowdhury, Jerome Martin, Christophe Ringeval, Vincent Vennin, Inflation after Planck: Judgment Day (arxiv:1902.03951)

• Swagat S. Mishra, Varun Sahni, Canonical and Non-canonical Inflation in the light of the recent BICEP/Keck results [arXiv:2202.03467]

• M. Chaichian, A. Ghal’e, M. Oksanen, An alternative approach to the Starobinsky model for inflation scenario [arXiv:2211.05212]

Review and exposition includes

• Alex Kehagias, Azadeh Moradinezhad Dizgah, Antonio Riotto, Comments on the Starobinsky Model of Inflation and its Descendants, Phys. Rev. D 89, 043527 (2014) (arXiv:1312.1155)

• Sergei Ketov, PLANCK mission, Starobinsky inflation and its realization in old-minimal supergravity, talk at Kavli IPMU Workshop: SUSY Model Building and Phenomenology, 2-4 December 2013 (pdf)

• John Ellis, Planck-Compatible Inflationary Models, talk 2013 (pptx)

• Andrei Linde, Inflationary Cosmology after Planck 2013 (arXiv:1402.0526)

• Jörg Rachen, The Planck 2015 Results: Cosmology and Fundamental Physics from the Polarised CMB and Other Probes, IMAPP Special Seminar, Nijmegen, Feb.5, 2015

• Ioannis Dalianis, Features and implications of the plateau inflationary potentials, Planck 2015 conference contribution (arXiv:1602.05026)

• George P. Efstathiou on behalf of the PLANCK mission, The PLANCK legacy, inflation and the origin of structure in the universe, talk at University of Cambridge, January 28, 2019 (recording from 50:49)

Discussion with more general higher curvature corrections:

• Gustavo Arciniega, Jose D. Edelstein, Luisa G. Jaime, Towards purely geometric inflation and late time acceleration (arXiv:1810.08166)

• Gustavo Arciniega, Pablo Bueno, Pablo A. Cano, Jose D. Edelstein, Robie A. Hennigar, Luisa G. Jaimem, Geometric Inflation (arXiv:1812.11187)

• Shunsuke Toyama, Sergei V. Ketov: Starobinsky inflation beyond the leading order [arXiv:2407.21349]

Discussion of eternal inflation in Starobinsky-type models

• Gabriela Barenboim, William Kinney, Wan-Il Park, Eternal Hilltop Inflation, Journal of Cosmology and Astroparticle Physics, Volume 2016, May 2016 (arXiv:1601.08140)

See also:

• Dhong Yeon Cheong, Hyun Min Lee, Seong Chan Park, Beyond the Starobinsky model for inflation (arXiv:2002.07981)

• Didam Duniya, Amare Abebe, Alvaro de la Cruz-Dombriz, Peter Dunsby, Imprint of $f(R)$ gravity in the cosmic magnification [arXiv:2210.09303]

Embedding into supergravity

Discussion of embedding of Starobinsky inflation in supergravity originates in

• Sergio Cecotti, Higher derivative supergravity is equivalent to standard supergravity coupled to matter, Phys. Lett. B 190 86 (1987) [doi:10.1016/0370-2693(87)90844-6]

• S. Cecotti, Sergio Ferrara, M. Porrati and S. Sabharwal, Nucl. Phys. B 306, 160 (1988).

and is further developed in the following articles:

• Sergei Ketov, Supergravity and Early Universe: the Meeting Point of Cosmology and High-Energy Physics, Int.J.Mod.Phys. A28 (2013) 1330021 (arXiv:1201.2239)

• John Ellis, Dimitri Nanopoulos, Keith Olive, No-Scale Supergravity Realization of the Starobinsky Model of Inflation Phys. Rev. Lett. 111, 111301 (2013) (arXiv:1305.1247)

• Renata Kallosh, Andrei Linde, Superconformal generalizations of the Starobinsky model JCAP 1306, 028 (2013) (arXiv:1306.3214)

• John Ellis, Dimitri Nanopoulos, Keith Olive, Starobinsky-like Inflationary Models as Avatars of No-Scale Supergravity JCAP 1310, 009 (2013) (arXiv:1307.3537)

• Fotis Farakos, Alex Kehagias, A. Riotto, On the Starobinsky Model of Inflation from Supergravity, Nucl. Phys. B 876, 187 (2013) (arXiv:1307.1137)

• Sergio Ferrara, Renata Kallosh, Andrei Linde and M. Porrati, Minimal Supergravity Models of Inflation (arXiv:1307.7696)

• Andrei Linde and M. Porrati, Higher Order Corrections in Minimal Supergravity Models of Inflation (arXiv:1309.1085)

• Sergio Ferrara, Renata Kallosh, Antoine Van Proeyen, On the Supersymmetric Completion of R+R2 Gravity and Cosmology JHEP 1311, 134 (2013) (arXiv:1309.4052)

• Sergei Ketov, Takahiro Terada, Old-minimal supergravity models of inflation, JHEP12(2013)040 (arXiv:1309.7494)

• Sergio Ferrara], Pietro Fre and A. S. Sorin, On the Topology of the Inflaton Field in Minimal Supergravity Models (arXiv:1311.5059)

• Jean Alexandre, Nick Houston, Nick E. Mavromatos, Starobinsky-type Inflation in Dynamical Supergravity Breaking Scenarios, Phys. Rev. D 89, 027703 (2014) (arXiv:1312.5197)

  via gravitino condensation, based on

  • Jean Alexandre, Nick Houston, Nick E. Mavromatos, Dynamical Supergravity Breaking via the Super-Higgs Effect Revisited, Phys. Rev. D 88, 125017 (2013) (arXiv:1310.4122)

  • Jean Alexandre, Nick Houston, Nick E. Mavromatos, Inflation via Gravitino Condensation in Dynamically Broken Supergravity, International Journal of Modern Physics D, Volume 24, Issue 04, April 2015 (arXiv:1409.3183)

• Sergei Ketov, Aleksei Starobinsky, Inflation and non-minimal scalar-curvature coupling in gravity and supergravity, JCAP 1208, 022 (2012) (arXiv:1203.0805)

• Sergei Ketov, S. Tsujikawa, Consistency of inflation and preheating in $F(R)$ supergravity, Phys. Rev. D 86, 023529 (2012) (arXiv:1205.2918)

• Sergei Ketov, On the supersymmetrization of inflation in $f(R)$ gravity,Prog. Theor. Exp. Phys. 2013, 123B04 (arXiv:1309.0293)

• Sergio Ferrara, Alex Kehagias, Antonio Riotto, The Imaginary Starobinsky Model and Higher Curvature Corrections (arXiv:1405.2353)

• Sergio Ferrara, Alex Kehagias, Higher Curvature Supergravity, Supersymmetry Breaking and Inflation (arXiv:1407.5187)

• Ioannis Dalianis, Fotis Farakos, Alex Kehagias, A. Riotto, Rikard von Unge, Supersymmetry Breaking and Inflation from Higher Curvature Supergravity (arXiv:1409.8299)

• Ioannis Dalianis, Fotis Farakos, On the initial conditions for inflation with plateau potentials: the $R + R^2$ (super)gravity case, Journal of Cosmology and Astroparticle Physics, Volume 2015, July 2015, (arXiv:1502.01246)

• Spyros Basilakos, Nick E. Mavromatos, Joan Sola, Starobinsky-like inflation and running vacuum in the context of Supergravity (arXiv:1505.04434)

  In this paper we have shown that SUGRA models with a dynamically induced massive gravitino phase lead to the RVM behavior and therefore provide a strong support for a fundamental description of the cosmic history.

• Andrea Addazi, Sergei Ketov, Energy conditions in Starobinsky supergravity (arXiv:1701.02450)

• John Ellis, Dimitri V. Nanopoulos, Keith Olive, From $R^2$ Gravity to No-Scale Supergravity, Phys. Rev. D 97, 043530 (2018) (arXiv:1711.11051)

• Hiroyuki Abe, Yermek Aldabergenov, Shuntaro Aoki, Sergei Ketov, Massive vector multiplet with Dirac-Born-Infeld and new Fayet-Iliopoulos terms in supergravity (arXiv:1808.00669)

• Sergey Ketov, Maxim Khlopov, Extending Starobinsky inflationary model in gravity and supergravity (arXiv:1809.09975)

• John Ellis, Dimitri Nanopoulos, Keith Olive, Sarunas Verner, A Unified No-Scale Model of Modulus Fixing, Inflation, Supersymmetry Breaking and Dark Energy, Phys. Rev. D 100, 025009 (2019) (arXiv:1903.05267, doi:10.1103/PhysRevD.100.025009)

• Yermek Aldabergenov, Shuntaro Aoki, Sergei Ketov, Minimal Starobinsky supergravity coupled to dilaton-axion superfield (arXiv:2001.09574)

• John Ellis, Marcos A. G. Garcia, Natsumi Nagata, Dimitri Nanopoulos, Keith Olive, Sarunas Verner, Building Models of Inflation in No-Scale Supergravity (arXiv:2009.01709)

• N. E. Martínez-Pérez, C. Ramírez, V. Vázquez-Báez, FRW supersymmetric model of Starobinsky (arXiv:2110.00556)

Embedding into 11d supergravity

Discussion of Starobinsky inflation in 11-dimensional supergravity with its higher curvature corrections included (see there):

• Katrin Becker, Melanie Becker, Supersymmetry Breaking, M-Theory and Fluxes, JHEP 0107:038,2001 (arXiv:hep-th/0107044)

• Kazuho Hiraga, Yoshifumi Hyakutake, Inflationary Cosmology via Quantum Corrections in M-theory (arXiv:1809.04724)

• Kazuho Hiraga, Yoshifumi Hyakutake, Scalar Cosmological Perturbations in M-theory with Higher Derivative Corrections (arxiv:1910.12483)

Embedding into superstring theory

Embedding of Starobinsky inflation into superstring theory is discussed in

• Costas Kounnas, Dieter Luest, Nicolaos Toumbas, $\mathcal{R}^2$ inflation from scale invariant supergravity and anomaly free superstrings with fluxes (arXiv:1409.7076)

• Ralph Blumenhagen, Anamaria Font, Michael Fuchs, Daniela Herschmann, Erik Plauschinn, Towards Axionic Starobinsky-like Inflation in String Theory, Physics Letters B Volume 746, 30 June 2015, Pages 217–222 (arXiv:1503.01607)

• John Ellis, Marcos A. G. Garcia, Dimitri Nanopoulos, Keith Olive, Phenomenological Aspects of No-Scale Inflation Models (arXiv:1503.08867)

• Luis Alvarez-Gaume, Alex Kehagias, Costas Kounnas, Dieter Luest, Antonio Riotto, Aspects of Quadratic Gravity (arXiv:1505.07657)

• Benedict Broy, David Ciupke, FranciscoG. Pedro, Alexander Westphal, Starobinsky-Type Inflation from $\alpha'$-Corrections, JCAP01(2016)001 (arXiv:1509.00024)

• K. Sravan Kumar, Inflaton candidates: from string theory to particle physics, PhD thesis (arXiv:1808.03701)

Concerning further higher curvature corrections:

• Sergei Ketov, Ekaterina O. Pozdeeva, Sergey Yu. Vernov, On the superstring-inspired quantum correction to the Starobinsky model of inflation [arXiv:2211.01546]

On quasi-realistic “flipped” $SU(5)$-GUT, modeled in 4d heterotic string theory and subsuming realistic Starobinsky-type cosmic inflation:

• Ignatios Antoniadis, John Ellis, John S. Hagelin, Dimitri Nanopoulos, The flipped $SU(5) \times U(1)$ string model revamped, Physics Letters B 231 1–2 (1989) 65-74 [doi:10.1016/0370-2693(89)90115-9]

• Ignatios Antoniadis, Dimitri Nanopoulos, John Rizos, Cosmology of the string derived flipped $SU(5)$, J. Cosm. Astrop. Phys 03 (2021) 017 [arXiv:2011.09396, doi:10.1088/1475-7516/2021/03/017]

• Ignatios Antoniadis, Dimitri Nanopoulos, John Rizos, Particle physics and cosmology of the string derived no-scale flipped $SU(5)$, Eur. Phys. J. C 82 (2022) 377 [arXiv:2112.01211, doi:10.1140/epjc/s10052-022-10353-6]