nLab quantum gravity
Context
Gravity
Formalism
Definition
Spacetime configurations
Properties
Spacetimes
| black hole spacetimes | vanishing angular momentum | positive angular momentum |
|---|---|---|
| vanishing charge | Schwarzschild spacetime | Kerr spacetime |
| positive charge | Reissner-Nordstrom spacetime | Kerr-Newman spacetime |
Quantum theory
Physics
physics, mathematical physics, philosophy of physics
Surveys, textbooks and lecture notes
theory (physics), model (physics)
experiment, measurement, computable physics
-
-
-
Axiomatizations
-
Tools
-
Structural phenomena
-
Types of quantum field thories
-
Contents
Idea
A theory of quantum gravity (QG) is supposed to be a quantum field theory (QFT) – or something similar – that corresponds to the classical field theory of gravity, possibly by quantization.
The key technical problem with quantum gravity as a non-perturbative quantum field theory is that all known constructions of QFTs quantize fields defined on a given spacetime background, while, in contrast, the field of gravity is that spacetime.
Since even for field theories that are defined on space-time backgrounds, such as Yang-Mills theory, non-perturbative quantization is a big open problem away from toy examples (for Yang-Mills theory it has been dubbed one of the Millennium Problems, see at quantization of Yang-Mills theory) this means that non-perturbative quantum gravity is an even wider open problem.
However, the Einstein-Hilbert action that defines gravity may be expanded around any of its solutions to the Einstein equations and the resulting perturbation of the field of gravity around this background behaves, to low order, like an ordinary field on a fixed spacetime background. This allows to treat perturbative quantum gravity (pQG) as a perturbative quantum field theory, see the references below.
While the Einstein-Hilbert action (or any of its variants) that defines the dynamics of gravity makes perfect sense at low energies as the definition of an effective quantum field theory (see there for details), it is not expected to be a non-effective theory at arbitrary high energies, because it is not renormalizable: all non-renormalizable QFTs that have appeared in practice turned out to be effective QFT approximations (see there) to renormalizable UV-completions.
The idea has been explored that gravity is simply to be regarded as a classical field theory, but trying to couple such a classical field theory to a stress-energy tensor of a matter quantum field theory leads to conceptual problems that break the very foundation of what is known about theoretical physics. The technical problem is this: the equations of motion of classical Einstein gravity (Einstein's equations) assert that the Einstein tensor of the field (physics) of gravity equals the energy-momentum tensor of all other force and matter fields. Here into the energy-momentum tensor enters the expression for energy and momentum of classical matter fields. However, according to the standard model of particle physics, these matter fields are not described by classical field theory. This then is the technical problem: there is no consistent way in sight to modify Einstein's equations so as to have a quantum EM tensor in it. The simple idea of taking the expectation value of the quantum matter EM-tensor leads to all kinds of theoretical problems.
Thus, this idea seems to be very unlikely. At the same time, it is clear that present experiments cannot directly probe the effects of that supposed UV-completion of Einstein-gravity.
Approaches to a full quantization of gravity therefore roughly fall into two different strategies
-
One assumes that the Einstein-Hilbert action is indeed the effective QFT that approximates a “UV-completion”, a more fundamental theory valid at all energies. This is the approach taken for instance in string theory.
-
One assumes that by some other fact that has been overlooked, one can make sense of a non-perturbative quantization of the EH action at arbitrary energies after all. This is for instance the case in speculations that EH-gravity has a UV fixed point?.
Accordingly, there are various proposals for what quantum gravity might be, but a comprehensive theory is missing to date. This is in stark contrast to the situation for the other fundamental forces of the standard model of particle physics: these are Yang-Mills fields, whose nature as QFTs is, while subtle, well understood. Indeed, the theoretical and experimental sucess of Yang-Mills theory is the main reason for the belief that QFT is the right framework for fundamental physics, and that also the field of gravity must have a description in this form.
Indeed, a model of fundamental physics where Yang-Mills fields are quantized but gravity is not is incomplete and arguably even inconsistent. Central motivating examples for this come from black hole-physics:
-
The study of quantum fields on the classical gravitational background of a black hole spacetime suggest that in a full theory of quantum gravity black holes could be shown to emit radiation and to eventually even decay in some way or other. This expected decay process cannot be described without a theory of quantum gravity.
-
Related to black hole radiation is a whole series of observations in classical general relativity that seem to indicate that black holes need to be thought of as systems possessing physical microstates with an entropy that cannot be accounted for by classical general relativity. This has led to the expectation that these microstates are states in quantum theory of gravity and that their understanding is necessary for understanding the physics of black holes.
-
More generally, appearances of unphysical singularities in general relativity, such as in black holes or cosmological singularities such as the big bang, have been argued to be artefacts of a non-quantum description of gravity. Various toy models of quantum gravity have been proposed where notably the big-bang singularity is just a classical approximation to a non-singular and well-defined quantum dynamics.
An evident definition of quantum gravity would seem to simply be the quantization of the Einstein-Hilbert action by the rules perturbation theory and renormalization. This straightforward approach however fails, as it can be demonstrated that this action functional is not renormalizable.
More recently it has been argued that there is evidence that the EH-action has a nontrivial UV-fixed point? after all. If true this would mean that a quantization of gravity in standard QFT is possible.
Another possibility is that this is only an apparent problem, and that standard gravity is nothing but an effective quantum field theory. (See there for references on gravity).
But most approaches to the problem have taken the non-renormalizability of classical gravity to be an indication that the standard concepts of QFT might need refinement in order to include gravity.
A common idea is that the assumption that the space of configurations in gravity is really that of smooth spacetimes, i.e. of smooth manifolds, is wrong. A plethora of variants of the notion of smooth manifold have been proposed as ingredients for a theory of quantum gravity. Notably concepts in noncommutative geometry. For instance Alain Connes‘s spectral action generalizes the Einstein-Hilbert action functional from Riemannian manifolds to spectral triples. However, none of the modifications of the spaces of configuratations of gravity proposed so far have been shown to support action functionals that can actually be quantized, in one sense or another.
Accordingly there are suggestions to modify instead the principles of perturbative quantum field theory. In string theory the fundamental assumption is that the Feynman perturbation series over 1-dimensional graphs of traditional perturbative QFT is to be refined by a similar series over 2-dimensional surfaces. It has been shown that this string perturbation series needs no renormalization and that it does describe Yang-Mills fields and a gravitational field. This led to huge hopes and large activity in the study of string theory as a theory of quantum gravity. But various central questions remain open and the state of the theory remains somewhat inconclusive.
While perturbative string theory did demonstrate that there is a variant of the perturbation series for gravity which is renormalized, it can, by definition of perturbation theory, be just an approximation to a more fundamental non-perturbatively defined theory. Various candidates for the non-perturbative theory to which the string perturbation series might be an approximation have been proposed. One that enjoyed a large popularity in the 1990s was called matrix mechanics but the high hopes connected with it were supported mostly by toy example computations. More recently the AdS/CFT correspondence is widely thought of as providing a non-perturbative definition of string theory and of quantum gravity. This correspondence asserts that observables of a string theory on an asymptotically anti-de Sitter spacetime may be matched equivalently to certain observables in an auxiliary super Yang-Mills theory. If true, this would allow to take the well understood non-perturbative definition of Yang-Mills theory and deduce from it a theory of quantum gravity.
Still another suggestion has been that ordinary quantum field theory might be seen to apply to the ordinary configuration space and action functional of general relativity, if only a suitably adapted parameterization of the configuration space is chosen. Notably one observes that Riemannian manifolds may be encoded in terms of connections on the tangent bundle – the Levi-Civita connection – this being manifestly analogous to the nature of the fields in Yang-Mills theory. (See first-order formulation of gravity).
It has been suggested that therefore quantum gravity may have a description in terms of the holonomy-observables of these connections, their parallel transport around loops. Research in this direction has therefore become known as loop quantum gravity . However, little progress has been made in understanding the configuration space of smooth connections in terms of loop observables. In most of the LQG-literature instead it is assumed from the outset that it makes sense to pass to generalized connections : while a smooth connection is the same as a smooth parallel transport-functor on the path groupoid , the “generalized connections” in this context are taken to be non-smooth and non-continuous such functors on sub-categories of paths. It is is not clear how this configuration space relates to that of ordinary gravity.
A plethora of further suggestions has developed out of this, which in the literature often still go under the name “LQG”, even though they may abandon the description of configuration spaces of metrics in terms of loop observables. There is for instance the approach of spin foams or causal dynamical triangulations, and that of causets , to name just a few.
The problem with discriminating between all these proposals is the combination of two problems.
-
There exist insufficient theoretical tools for analyzing in detail the consequences of the various proposals.
-
There are few to no experiments available that would be able to observe the phenomena that a theory of quantum gravity is supposed to describe.
As a result, the field of fundamental physics today finds itself in a somewhat awkward position where the need for theoretical progress concerning quantum gravity for conceptual reasons is widely appreciated, but where disagreements about the viability of various proposals finds no conclusive resolution and divides the community.
Effects
First quantum correction to Newtonian -potential
The first order quantum correction to the classical gravitational potential
between two bodies of mass , , respectively, may be computed unambiguously in perturbative quantum gravity (Donoghue 95, Section 9):
The result is a term of the form
(where is the number of massless neutrino-species, is the gravitational constant, is the speed of light and is Planck's constant).
Here for fm we have that the quantum correction is by a tiny factor of order
Vacuum energy and Cosmological constant
The renormalization freedom in perturbative quantization of gravity induces freedom in the choice of vacuum expectation value of the stress-energy tensor and hence in the cosmological constant.
For details see there.
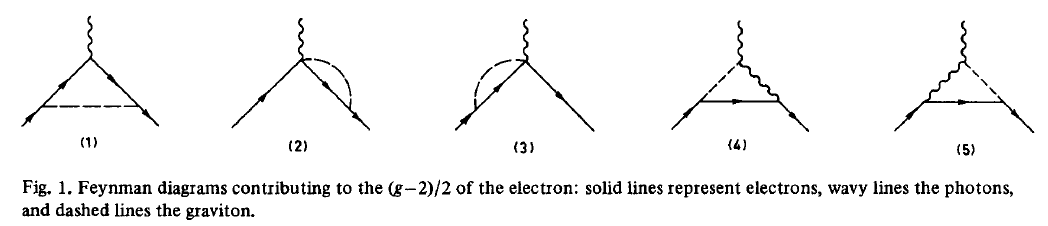
Anomalous magnetic moment of the leptons
The corrections of 1-loop perturbative quantum gravity to the anomalous magnetic moment of the electron and the muon have been computed in (Berends-Gastman 75) and found to be finite, without need for renormalization. These Feynman diagrams contribute:
Approaches
Some proposed proposals towards a more fundamental theory of quantum gravity:
Special cases
Related concepts
References
General
Early mentioning of potential breakdown of classical geometry at microscopic scales:
-
Bernhard Riemann, Über die Hypothesen, welche der Geometrie zu Grunde liegen, Göttingen (1845) [doi:10.1007/978-3-642-35121-1]
Engl. transl: William Clifford: On the hypotheses which underlie geometry, Nature VIII (1873) 183-184 [doi:10.1007/978-3-319-26042-6]
[§III.3] Now it seems that the empirical notions on which the metric determinations of Space are based, the concept of a solid body and a light ray, lose their validity in the infinitely small; it is therefore quite definitely conceivable that the metric relations of Space in the infinitely small do not conform to the hypotheses of geometry; and in fact, one ought to assume this as soon as it permits a simpler way of explaining phenomena.
Original discussion of the Wheeler-DeWitt equation:
- Bryce DeWitt, (5.5) in: Quantum Theory of Gravity. I. The Canonical Theory, Phys. Rev. 160 (1967) 1113 [doi:10.1103/PhysRev.160.1113]
Compilation of early articles:
- Alexander S. Blum, Dean Rickles (eds.): Quantum Gravity in the First Half of the Twentieth Century, Sources 10, Edition Open Access (2018) [doi:10.34663/9783945561317-00, pdf]
Accounts of the early history of the subject:
-
Cécile DeWitt-Morette, The Pursuit of Quantum Gravity – Memoirs of Bryce DeWitt from 1946 to 2004, Springer (2011) [doi:10.1007/978-3-642-14270-3_4]
-
Dean Rickles: Covered with Deep Mist – The Development of Quantum Gravity (1916-1956), Oxford University Press (2020) [ISBN:9780199602957, oup:40408]
On the standard lore concerning necessity of and the problems of quantum gravity:
-
Steve Carlip: Quantum Gravity: a Progress Report [arXiv:gr-qc/0108040]
-
Richard Woodard: How Far Are We from the Quantum Theory of Gravity? [arXiv:0907.4238]
-
Hermann Nicolai: Quantum Gravity: The View from Particle Physics, Fundam. Theor. Phys. 177 (2014) 369-387 [arXiv:1301.5481, doi:10.1007/978-3-319-06349-2_18]
-
Steven Carlip, Dah-Wei Chiou, Wei-Tou Ni, Richard Woodard: Quantum Gravity: A Brief History of Ideas and Some Prospects, Int. J. Mod. Phys. D [arXiv:1507.08194]
-
Karen Crowther: Why Do We Want a Theory of Quantum Gravity?, Cambridge Elements in Philosophy of Physics, Cambridge University Press (2025) [ISBN:9781108878074, doi:10.1017/9781108878074, arXiv:2505.04858]
Exposition from the point of view of worldline formalism:
- Edward Witten, Quantum Gravity, Solomon Lefschetz Memorial Lecture Series, November 2011 (video)
Lecture notes on various aspects:
- Ivano Basile, Luca Buoninfante, Francesco Di Filippo, Benjamin Knorr, Alessia Platania, Anna Tokareva: Lectures in Quantum Gravity, lectures at Towards Quantum Gravity, Nordita (2024) [arXiv:2412.08690, videos:YT]
Surveys of the state of and perspectives on the field:
-
Claus Kiefer, Quantum Gravity, Oxford University Press (2007) [doi:10.1093/acprof:oso/9780199585205.001.0001]
-
Visions in Quantum Gravity, notes from participants of Quantum Gravity: from gravitational EFTs to UV complete approaches, Nordita (2024) [arXiv:2412.08696, videos]
As a perturbative quantum field theory
As a perturbative quantum field theory, quantum gravity exists (usually thought of as an effective quantum field theory):
-
Richard Feynman, Quantum theory of gravitation, Acta Phys. Polon. 24 (1963) 697-722 [spire:9148]
-
Martinus Veltman, Quantum theory of Gravitation, In Les Houches 1975, Proceedings, Methods In Field Theory, (Amsterdam 1976) 265-327 [pdf, spire]
-
John Donoghue, General relativity as an effective field theory: The leading quantum corrections, Phys. Rev. D 50 (1994) 3874-3888 [arXiv:gr-qc/9405057]
-
Vlad-Mihai Mandric, Tim R. Morris, Dalius Stulga, Off-shell divergences in quantum gravity [arXiv:2308.07382]
Introduction, review and outlook:
-
John Donoghue, Introduction to the Effective Field Theory Description of Gravity [arXiv:gr-qc/9512024, spire]
-
Zvi Bern, Perturbative Quantum Gravity and its Relation to Gauge Theory, Living Rev. Relativ. 5 1 (2002) 5 [arXiv:gr-qc/0206071, doi:10.12942/lrr-2002-5]
-
Cliff Burgess, Quantum Gravity in Everyday Life: General Relativity as an Effective Field Theory, Living Rev. Rel. 7 5 (2004) [arXiv:gr-qc/0311082, doi:10.12942/lrr-2004-5]
-
Richard Woodard, Perturbative Quantum Gravity Comes of Age, International Journal of Modern Physics DVol. 23, No. 09, 1430020 (2014) (arXiv:1407.4748)
-
Ilya L. Shapiro, The background information about perturbative quantum gravity, in: Handbook of Quantum Gravity, Springer (2023) [arXiv:2210.12319]
-
John F. Donoghue, Quantum General Relativity and Effective Field Theory, in: Handbook of Quantum Gravity, Springer (2023) [arXiv:2211.09902]
-
John F. Donoghue, General Relativity as a Perturbative Quantum Field Theory, lecture series at Basics of Quantum Gravity, ISQG (2023) [web]
-
John Donoghue, Quantum General Relativity as an EFT, podcast discussion on Theoretically Podcasting, Aug (2023) [video: YT]
-
BBDKPT24, sections 2 & 3
Aspects of gauge invariance:
- Petr M. Lavrov, Ilya Shapiro, Gauge invariant renormalizability of quantum gravity, in Handbook of Quantum Gravity, Springer (2023) [arXiv:2210.09271]
A brief survey of the relevant mathematical issues with more pointers to the literature:
- Igor Khavkine, Gravity: an exercise in quantization, talk at Quantum Gravity in Perspective, Munich, 31 May 2013 (pdf slides, video)
The rigorous construction via causal perturbation theory of quantum gravity as a perturbative quantum field theory around Minkowski spacetime is spelled out in
- Günter Scharf, Quantum Gauge Theories – A True Ghost Story, Wiley 2001
The generalization of this to perturbation about curved spacetimes is discussed via locally covariant perturbative algebraic quantum field theory in
- Romeo Brunetti, Klaus Fredenhagen, Katarzyna Rejzner, Quantum gravity from the point of view of locally covariant quantum field theory, Communications in Mathematical Physics August 2016, Volume 345, Issue 3, pp 741–779 (arXiv:1306.1058)
and with applications to cosmology in
- Romeo Brunetti, Klaus Fredenhagen, Thomas-Paul Hack, Nicola Pinamonti, Katarzyna Rejzner, Cosmological perturbation theory and quantum gravity, Journal of High Energy Physics August 2016:32 (arXiv:1605.02573)
Regarding the cosmological constant:
-
John Donoghue: The cosmological constant and the use of cutoffs, Phys. Rev. D 104 045005 (2021) [arXiv:2009.00728, doi:10.1103/PhysRevD.104.045005]
-
David Prinz, On Perturbative Quantum Gravity with a Cosmological Constant [arXiv:2303.14160]
-
John Donoghue: Do and run? [arXiv:2412.08773]
Corrections at 1-loop from quantum gravity to the anomalous magnetic moment of the leptons are discussed in
- F. A. Berends, R. Gastmans, Quantum gravity and the electron and muon anomalous magnetic moment, Phys. Lett. B55 Issue 3 Feb 1975 311-312 (doi:10.1016/0370-2693(75)90608-5)
and adapted to supergravity in
- F. del Aguila, A. Culatti, R. Munoz-Tapia, M. Perez-Victoria, Supergravity corrections to in differential renormalization, Nuclear Physics B 504 (1997) 532-550 (arXiv:hep-ph/9702342)
See also:
- F. T. Brandt, J. Frenkel, D. G. C. McKeon, Quantum gravity in a general background gauge [arXiv:2208.13004]
Concrete discussion of graviton scattering amplitudes:
- S. Abreu, F. Febres Cordero, H. Ita, M. Jaquier, B. Page, M. S. Ruf, V. Sotnikov, The Two-Loop Four-Graviton Scattering Amplitudes (arXiv:2002.12374)
With an emphasis on the S-matrix-perspective:
- Pierre Vanhove, S-matrix approach to general gravity and beyond (arXiv:2104.10148)
On perturbative quantum gravity via string-localized quantum fields:
- Christian Gaß, José M. Gracia-Bondía, Karl-Henning Rehren, Quantum general covariance [arXiv:2304.09843]
See also:
- Enrico Herrmann, Murat Kologlu, Ian Moult: Energy Correlators in Perturbative Quantum Gravity [arXiv:2412.05384]
For more discussion of perturbative supergravity see at
Non-renormalizablity
That pure Einstein gravity is not perturbatively renormalizable at 2-loops was shown in
-
M. H. Goroff, A. Sagnotti, Quantum Gravity At Two Loops, Phys. Lett. B 160 (1985) 81.
-
A. E. M. van de Ven, Two loop quantum gravity, Nucl. Phys. B 378 (1992) 309.
For generic matter couplings this applies already at 1-loop:
-
Gerard 't Hooft, Martinus Veltman, Annales Poincare Phys. Theor. A 20 , 69 (1974)
-
Gerard 't Hooft, Nucl. Phys. B 62, 444 (1973);
-
Stanley Deser, Peter van Nieuwenhuizen, Phys. Rev. D 10, 401 (1974);
-
Stanley Deser, H. S. Tsao and Peter van Nieuwenhuizen, Phys. Rev. D 10 , 3337 (1974)
If the matter coupling is such as to make the theory supersymmetric (supergravity), the divergence appears only in higher loop order.
That it appears earliest at 3-loops was established in
-
M. T. Grisaru, Phys. Lett. B 66, 75 (1977);
-
E. T. Tomboulis, Phys. Lett. B67, 417 (1977);
-
Stanley Deser, J. H. Kay and Kellogg Stelle, Phys. Rev. Lett. 38, 527 (1977);
-
Renata Kallosh, Phys. Lett. B99, 122 (1981);
-
Paul Howe, Kellogg Stelle and Paul Townsend, Nucl. Phys. B 236, 125 (1984).
Specifically for N=8 d=4 supergravity there is evidence that it might be finite at all loops. See the references there.
Review:
- Assaf Shomer: A pedagogical explanation for the non-renormalizability of gravity [arXiv:0709.3555, spire:761598]
From string field theory
Derivation of graviton-scattering amplitudes from string field theory:
-
Taejin Lee, Gravitational Scattering Amplitudes and Closed String Field Theory in the Proper-Time Gauge, EPJ Web of Conferences 168, 07004 (2018) (doi:10.1051/epjconf/201816807004)
-
Taejin Lee, Four-Graviton Scattering and String Path Integral in the Proper-time gauge (arXiv:1806.02702)
Local Gauging of global symmetries
It is being argued that after embedding into consistent quantum gravity, all global symmetries must become local symmetries.
A substantiation of this argument via AdS/CFT is given in
-
Daniel Harlow, Hirosi Ooguri, Symmetries in quantum field theory and quantum gravity (arXiv:1810.05338)
-
Daniel Harlow, Hirosi Ooguri, Constraints on symmetry from holography, Phys. Rev. Lett. 122, 191601 (2019) (arXiv:1810.05337)
See also:
- Sylvain Fichet, Prashant Saraswat, Approximate Symmetries and Gravity (arXiv:1909.02002)
3d Gravity and Chern-Simons theory
On 3-dimensional (quantum) gravity (general relativity) with cosmological constant, and its (non-)relation to Chern-Simons theory with non-compact gauge groups:
The original articles on 3d gravity, discussing its formulation as a Chern-Simons theory and discovering its holographic relation to a 2d CFT boundary field theory (well before AdS/CFT was conceived from string theory):
-
Stanley Deser, Roman Jackiw, Gerard 't Hooft, Three-dimensional Einstein gravity: Dynamics of flat space, Ann. Phys. 152 (1984) 220 (doi:10.1016/0003-4916(84)90085-X)
-
Stanley Deser, Roman Jackiw, Three-dimensional cosmological gravity: Dynamics of constant curvature, Annals of Physics, Volume 153, Issue 2, 1 April 1984, Pages 405-416 (doi:10.1016/0003-4916(84)90025-3, spire:192694)
-
Roman Jackiw, Lower dimensional gravity, Nuclear Physics B Volume 252, 1985, Pages 343-356 (doi:10.1016/0550-3213(85)90448-1, spire:204694)
-
J. D. Brown, Marc Henneaux, Central charges in the canonical realization of asymptotic symmetries: An example from three dimensional gravity, Commun. Math. Phys. (1986) 104: 207 (doi:10.1007/BF01211590)
-
A. Achucarro, Paul Townsend, A Chern-Simons Action for Three-Dimensional anti-De Sitter Supergravity Theories, Phys. Lett. B180 (1986) 89 (doi:10.1016/0370-2693(86)90140-1, spire:21208)
-
Steven Carlip, Inducing Liouville theory from topologically massive gravity, Nuclear Physics B Volume 362, Issues 1–2, 16 September 1991, Pages 111-124 (doi:10.1016/0550-3213(91)90558-F)
-
O. Coussaert, Marc Henneaux, P. van Driel, The asymptotic dynamics of three-dimensional Einstein gravity with a negative cosmological constant, Class. Quant. Grav. 12 (1995) 2961-2966 (arXiv:gr-qc/9506019)
The corresponding non-perturbative quantization of 3-dimensional gravity, via quantization of 3d Chern-Simons theory:
-
Edward Witten, (2+1)-Dimensional Gravity as an Exactly Soluble System, Nucl. Phys. B 311 (1988) 46. [doi:10.1016/0550-3213(88)90143-5
-
Herman Verlinde, Conformal field theory, two-dimensional quantum gravity and quantization of Teichmüller space, Nuclear Physics B 337 3 (1990) 652-680 [doi:10.1016/0550-3213(90)90510-K]
Review:
-
Steven Carlip, Lectures in (2+1)-Dimensional Gravity, J. Korean Phys. Soc. 28: S447-S467, 1995 (arXiv:gr-qc/9503024)
-
Steven Carlip, Quantum Gravity in 2+1 Dimensions, Cambridge Monographs on Mathematical Physics (2003) (publisher)
-
Steven Carlip, Quantum Gravity in 2+1 Dimensions: The Case of a Closed Universe, Living Rev. Rel. 8:1, 2005 (arXiv:gr-qc/0409039)
-
Steven Carlip, My Research – (2+1)-Dimensional quantum gravity
-
Laura Donnay, Asymptotic dynamics of three-dimensional gravity, Proceedings of Eleventh Modave Summer School in Mathematical Physics, POS 271 (2016) arXiv:1602.09021, doi:10.22323/1.271.0001
-
Wout Merbis, Chern-Simons-like Theories of Gravity (arXiv:1411.6888)
-
Chen-Te Ma, Einstein Gravity and Boundary Description: Pedagogical Review arXiv:2310.04665
Further developments:
-
Edward Witten, Three-dimensional gravity revisited (2007) [arXiv:0706.3359]
-
Paul Townsend, Massive 3d (super)gravity, slides, (pdf)
-
Gaston Giribet, Black hole physics and AdS3/CFT2 correspondence, lectures at Croatian Black Hole School 2010
-
Alan Garbarz, Gaston Giribet, Yerko Vásquez, Asymptotically AdS solutions to topologically massive gravity at special values of the coupling constants, arxiv/0811.4464
-
Rudranil Basu, Samir K Paul, Consistent 3D Quantum Gravity on Lens Spaces (arXiv:1109.0793)
-
Marc Henneaux, Wout Merbis, Arash Ranjbar, Asymptotic dynamics of gravity with two asymptotic regions (arXiv:1912.09465)
-
Viraj Meruliya, Sunil Mukhi, Palash Singh, Poincaré Series, 3d Gravity and Averages of Rational CFT (arXiv:2102.03136)
-
Scott Collier, Lorenz Eberhardt, Mengyang Zhang: Solving 3d Gravity with Virasoro TQFT, SciPost Phys. 15 151 (2023) [dou:10.21468/SciPostPhys.15.4.151, arXiv:2304.13650]
See also:
-
Nathan Benjamin, Scott Collier, Alexander Maloney, Pure Gravity and Conical Defects, Journal of High Energy Physics 2020 34 (2020) arXiv:2004.14428, doi:10.1007/JHEP09(2020)034]
-
T. Mursheed Amith, Alicia Castro: The massive BMS character in 3D quantum gravity [arXiv:2502.14578]
Last revised on June 13, 2025 at 07:47:47. See the history of this page for a list of all contributions to it.