nLab bireflective subcategory

Idea

By a bireflective subcategory one might mean:

1. A subcategory $\iota \,\colon\, \mathcal{C} \hookrightarrow \mathcal{B}$ which is both reflective and coreflective — i.e. a fully faithful functor possessing both left and right adjoints: $L \dashv \iota \dashv R$ (reflective localization and coreflective localization).

   The adjoint pair $\iota \circ L \dashv \iota \circ R$ is then an adjoint modality; see there for more.

2. More specifically, one may in addition ask that $L \simeq R$, hence that the subcategory inclusion $\iota$ has an ambidextrous adjoint $\beta \dashv \iota \dashv \beta$.

   Such subcategories are called quintessential localizations by Johnstone (1996).

   The corresponding (co-)monad $\natural \coloneqq \iota \circ \beta$ is then a Frobenius monad (see at classical modality).

3. Finally, one may moreover ask that the points-to-pieces transform $\natural \overset{\epsilon}{\longrightarrow} id \overset{\eta}{\longrightarrow} \natural$ of a quintessential localization be the identity morphisms.

   This strong form of the notion is the case actually called bireflective subcategories by Freyd et al. (1999).

Definition

Definition

A full subcategory-inclusion

$$\iota \;\colon\; \mathcal{C} \hookrightarrow \mathcal{B}$$

is bireflective in the sense of FOPTST99, Def. 8 iff

(1.) the inclusion has an ambidextrous adjoint

(2.) such that for all $E \in \mathcal{B}$ the counit of the right adjunction followed by the unit of the left adjunction (the points-to-pieces transform) equals the identity:

Remark

The first clause in Def. does not in general by itself enforce the second clause. A counter-example is given in FOPTST99, Rem. 12.

However, the second clause does follow automatically when $\mathcal{B}$ is a Cauchy-complete category (Johnstone (1996)).

Remark

In the other direction, the second clause in Def. implies that

is an idempotent natural endomorphism, exhibited as a split idempotent.

Proposition

Given a category $\mathcal{B}$, its bireflective subcategories (Def. ) are in correspondence with the split idempotent natural endomorphisms on $id_\mathcal{B}$ with specified splitting, i.e.

with

(1)$$\eta^\natural \,\circ\, \epsilon^\natural \;=\; \mathrm{id} \,.$$

(FOPTST99, Thm. 13)

Concretely, from a split idempotent on $id_{\mathcal{B}}$ we recover the Frobenius monad $\natural$ as follows:

Lemma

Given a split idempotent transformation as in Prop. we have for all $E \,\in\, \mathcal{B}$

$$\natural (\eta^{\natural}_{E}) \;=\; \eta^{\natural}_{\natural E} \;\;\;\;\;\; \text{and} \;\;\;\;\;\; \natural (\epsilon^{\natural}_{E}) \;=\; \epsilon^{\natural}_{\natural E} \,.$$

(RFL21, Lem. 7.7)

Proof

By naturality of the transformation $\eta$

and using (1) we get the first statement:

$$\natural (\eta^{\natural}_{E}) \;=\; \natural (\eta^{\natural}_{E}) \circ \overset { \mathrm{id}_E } { \overbrace{ \eta^\natural_E \circ \epsilon^\natural_E } } \;=\; \eta^\natural_{\natural E} \circ \eta^{\natural}_{E} \circ \epsilon^\natural_E \;=\; \eta^{\natural}_{\natural E}$$

The second follows analogously.

Proposition

Given a split idempotent transformation as in Prop. , $\natural \colon \mathcal{B} \to \mathcal{B}$ becomes

1. an idempotent monad $(\natural, \eta, \mu)$ by setting

   $$\mu \,\coloneqq\, \natural(\epsilon^\natural_{(-)})$$

2. an idempotent comonad $(\natural, \epsilon, \delta)$ by setting

   $$\delta \,\coloneqq\, \natural(\eta^\natural_{(-)})$$

(RFL21, Prop. 7.8)

Proof

For the associativity of the monoid product we need to show the commutativity of

By functoriality of $\natural$ this follows from the commutativity of

which holds by naturality of $\epsilon$.

The other claims follow similarly.

Modal type theory

A modal type theory for bireflection modalities has been proposed in Riley, Finster & Licata (2021), Riley (2022).

We show the inference rules which these authors propose to add to plain intuitionistic type theory for encoding the presence of a bireflection classical modality $\natural$ on the type system, and we show corresponding categorical semantics via commuting diagrams in an interpreting locally cartesian closed category (a more syntactic semantics is indicated in RFL21, Sec. 7, esp. Fig. 6).

Remark

Given a bireflection $\natural \colon \mathcal{B} \to \mathcal{B}$ as above, then for $\Gamma \in \mathcal{B}$ we obtain a monad on the slice category, to be denoted

(2)$$\natural_\Gamma \;\colon\; \mathcal{B}_{/\Gamma} \to \mathcal{B}_{/\Gamma}$$

by setting

$$\natural_\Gamma \left[ \begin{array}{c} A \\ \big\downarrow \mathrlap{\!\! {}^{p_A} } \\ \Gamma \end{array} \;\;\;\; \right] \;\;\coloneqq\;\; \big(\eta^\natural_\Gamma\big)^\ast \,\natural\, \left[ \begin{array}{c} \natural A \\ \big\downarrow \mathrlap{\!\! {}^{\natural p_A} } \\ \natural \Gamma \end{array} \;\;\;\; \right]$$

Remark

Beware of some non-obvious properties of the following type-theoretic syntax:

1. There is an asymmetry in the meaning of $\underline{(-)}$:

   An underline of a context denotes application of $\natural$, but an underline of a type in context only means its pullback along the counit $\epsilon^{\natural}$. The idea is that underlines indicate dependency on $\natural$-modal variables, to be distinguished of a type itself being $\natural$-modal or not.

2. The syntactic symbol “$\natural$” is not exactly interpreted as the bireflective monad of that name. Rather:

   • An unadorned “$\natural$” in the syntax interprets, in context $\Gamma$, as the relative monad

     $$\classical^{rel}_\Gamma \;\; \colon \;\; \array{ \mathcal{B}_{/\natural \Gamma} & \xrightarrow{ (\eta^\natural_\Gamma)^\ast } & \mathcal{B}_{/\Gamma} & \xrightarrow{ \natural_\Gamma } & \mathcal{B}_{/\Gamma} }$$

   • The combination $\natural \underline{(-)}$ is what actually interprets as $\natural_\Gamma$ (2).

     This transpires syntactically in RFL21, Cor. 2.14; Riley22, Cor. 1.1.16, and semantically in (3) below.

The list of inference rules and their categorical semantics (first the axioms then derived rules):

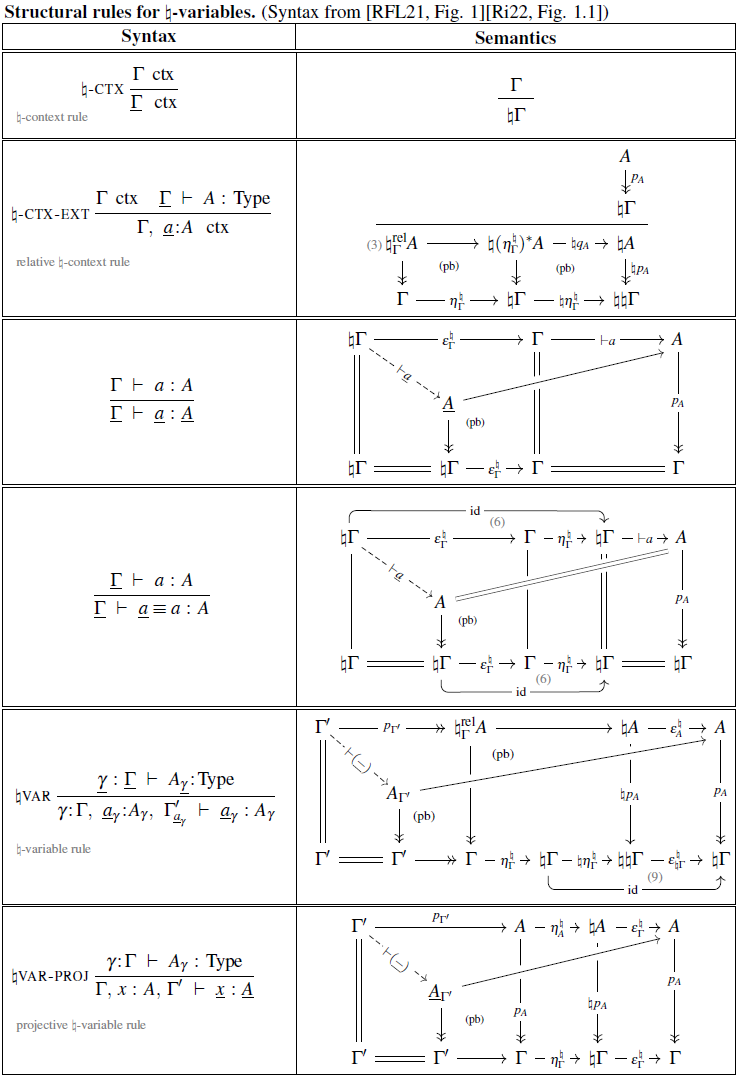
Using these ingredients, one finds that the function $a \,\mapsto\, \underline{a}^\natural$ is interpreted simply as postcomposition with the $\eta^{\natural}$-naturality square:

(3)$$\;$$

With this, one finds the following rule for $\natural$ respecting dependent pair types:

(4)$$\;$$

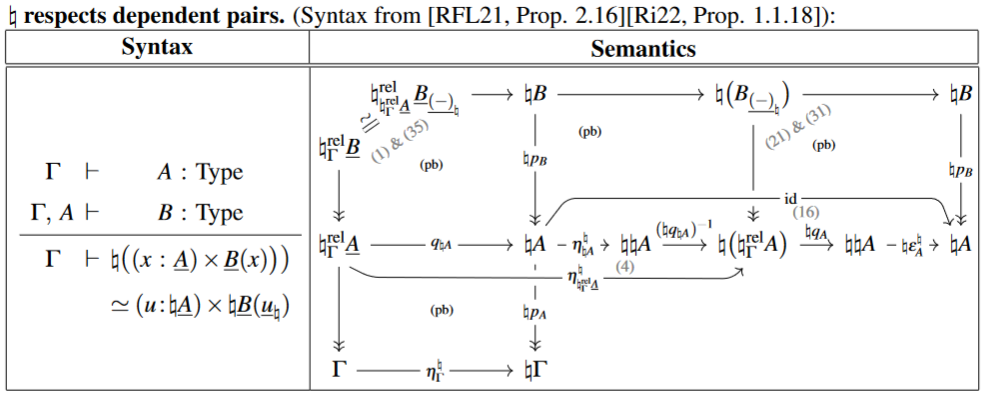
Using this one finds that every type $A$ is the dependent sum type of its fiber linear types $A_{\underline{x}}$ (NB: we show 1-categorical semantics, interpreting identification types as diagonal morphisms):

(5)$$\;$$

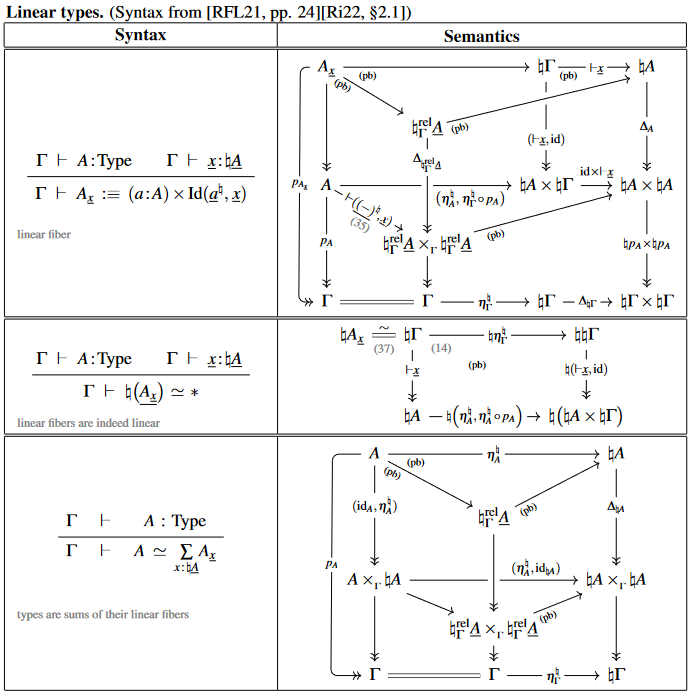
Examples

Example

(spaces among retractive spaces)
Let $\mathcal{B}$ be the category of retractive topological spaces (or just of Sets), i.e. the category of diagrams in Top (Set) of the form $B \xrightarrow{i} E \xrightarrow{p} B$ such that $p \circ i \,=\, id_B$. Then the functor

$$\begin{array}{ccc} Top &\hookrightarrow& Top_{\mathcal{R}} \\ B &\mapsto& \big[ B \xrightarrow{id} B \xrightarrow{id} B \big] \end{array}$$

is a bireflective subcategory inlusion (Def. ) with ambidextrous adjoint given by

$$\begin{array}{ccc} Top_{\mathcal{R}} &\longrightarrow& Top \\ \big[ B \xrightarrow{i} E \xrightarrow{p} B \big] &\mapsto& B \end{array}$$

Example

(zero-vector bundles among all vector bundles)
For any ground field, let $\mathcal{B} \coloneqq Vect_{Set} \coloneqq \int_{S \in Set} Vect S$ be the category VectBund of vector bundles over Sets, hence of indexed vector spaces. Then the functor

$$Set \xhookrightarrow{\;\; 0 \;\;} Vect_{Set}$$

which sends any set $S$ to the zero vector bundle $S \times \{0\}$ over $S$ is a bireflective subcategory in the sense of Def. .

Example

(zero-spectrum bundles among all parameterized spectra)
Let $T Grpd_\infty$ denote the $\infty$-category of parameterized spectra over varying $\infty$-groupoids (the tangent $\infty$-category of $Grpd_\infty$). Then the inclusion

$$Grpd_\infty \hookrightarrow T Grpd_\infty$$

given by sending $X \in Grpd_\infty$ to the zero-spectrum bundle over $X$ ought to count as a “bireflective sub-$\infty$-category” (cf. here at infinitesimal cohesion).

A model category-presentation of this situation by a (left and right) Quillen functor to a model structure for parameterized spectra underlying which is a bireflective sub-1-category inclusion (Def. ) may be recognized in Hebestreit, Sagave & Schlichtkrull (2020), Lem. 3.19, there incarnated as the canonical inclusion

$$\mathcal{S}^{\mathcal{I}} \hookrightarrow Sp^{\Sigma}_{\mathcal{R}}$$

of $\mathcal{I}$-spaces into symmetric spectra internal to retractive spaces (Exp. ).

An analogous statement is in Braunack-Mayer (2019), Cor. 2.45.

Related concepts

• infinitesimal cohesion

• classical modality

• VectBund

• parameterized spectra

References

Subcategories whose inclusion functor admits both a left and right adjoint are called bireflective in:

• W. John Wilbur, “Reflective and coreflective hulls in the category of locally convex spaces.” General topology and its applications 4.3 (1974): 235-254.

On subcategory inclusions with ambidextrous adjoints (quintessential localizations):

• Peter Johnstone, Remarks on Quintessential and Persistent Localizations, TAC 2 8 (1996) 90-99. [pdf, 2-08]

On subcategory inclusions with ambidextrous adjoints whose points-to-pieces transform is the identity (actual bireflective subcategories):

• Peter Freyd, Peter O’Hearn, A. John Power, M. Takeyama, Ross Street, Robert D. Tennent, Bireflectivity, Theoretical Computer Science 228 1–2 (1999) 49-76 [doi:10.1016/S0304-3975(98)00354-5]

Discussion of a modal type theory for bireflective modalities, in a context of linear homotopy type theory:

• Mitchell Riley, Eric Finster, Daniel R. Licata, Section 7.1 in: Synthetic Spectra via a Monadic and Comonadic Modality [arXiv:2102.04099]

• Mitchell Riley, A Bunched Homotopy Type Theory for Synthetic Stable Homotopy Theory, PhD Thesis (2022) [doi:10.14418/wes01.3.139, ir:3269, pdf]