nLab associativity
Context
Category theory
Concepts
Universal constructions
Theorems
Extensions
Applications
Higher category theory
Basic concepts
Basic theorems
-
homotopy hypothesis-theorem
-
delooping hypothesis-theorem
-
stabilization hypothesis-theorem
Applications
Models
- (n,r)-category
- Theta-space
- ∞-category/∞-category
- (∞,n)-category
- (∞,2)-category
- (∞,1)-category
- (∞,0)-category/∞-groupoid
- (∞,Z)-category
- n-category = (n,n)-category
- n-poset = (n-1,n)-category
- n-groupoid = (n,0)-category
- categorification/decategorification
- geometric definition of higher category
- algebraic definition of higher category
- stable homotopy theory
Morphisms
Functors
Universal constructions
Extra properties and structure
1-categorical presentations
Contents
Definition
In a category associativity is the condition that the two ways to use binary composition of morphisms to compose a sequence of three morphisms are equal
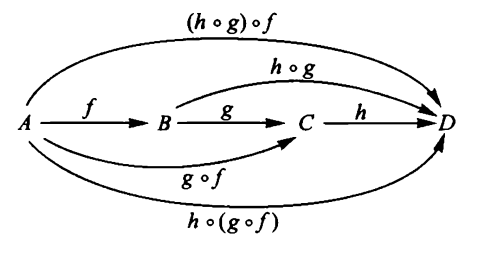
If the category has a single object it is the delooping a monoid , and then this condition is the associativity condition on the binary operation of monoids such as groups, rings, algebras, etc.
More generally, in higher category theory, associativity of composition of morphisms in an n-category means that the different ways to use binary composition for composing collections of k-morphisms form a contractible infinity-groupoid. This is a coherence law.
For instance the associativity law in an A-infinity algebra is the special case of associativity in a 1-object A-infinity-category.
Examples
-
See associahedron.
-
In a monoidal category associativity is the statement that the associator satisfies its coherence law, which is true by a coherence theorem.
Related concepts
References
The coherence law of associativity is stated in
- Hermann Grassmann, §3 of Ausdehnungslehre, 1844
Last revised on December 1, 2019 at 08:08:04. See the history of this page for a list of all contributions to it.