nLab cyclic loop stack
Context
Higher Geometry
higher geometry / derived geometry
Ingredients
Concepts
-
geometric little (∞,1)-toposes
-
geometric big (∞,1)-toposes
Constructions
Examples
-
derived smooth geometry
Theorems
Contents
Idea
Any free loop stack carries a canonical group action of the circle group , given by rigid rotation of loops (explicit models are discussed in Lupercio & Uribe 01, Sec. 3.6). This allows to form the further homotopy quotient/quotient stack by this action:
In analogy with cyclic loop spaces, this may be called the cyclic loop stack of .
Properties
Groupoid presentations
While this is a basic and canonical construction, there seems to be little to no explicit discussion of it in the literature (as of summer 2021). However, the concrete groupoid-presentations considered in Huan 18, Def. 2.5, 2.9, following Ganter 07, Sec. 2.1, may be understood as plausible proposals for models of (1).
Motivated from these definitions is, in turn, that of Huan's inertia orbifolds, whose orbifold K-theory defines a form of equivariant elliptic cohomology of .
General abstract characterization
Regarding
-
the stack as an object in the (∞,1)-topos of Smooth∞Groupoids (or DTopological∞Groupoids or whatever is appropriate),
-
the circle group as a (smooth) ∞-group with delooping/moduli ∞-stack ,
then (BMSS 19, Sec. 2.2) the cyclic loop stack is equivalently the right base change (dependent product) of along the point inclusion followed (when desired) by left base change (dependent sum) back to the absolute context:
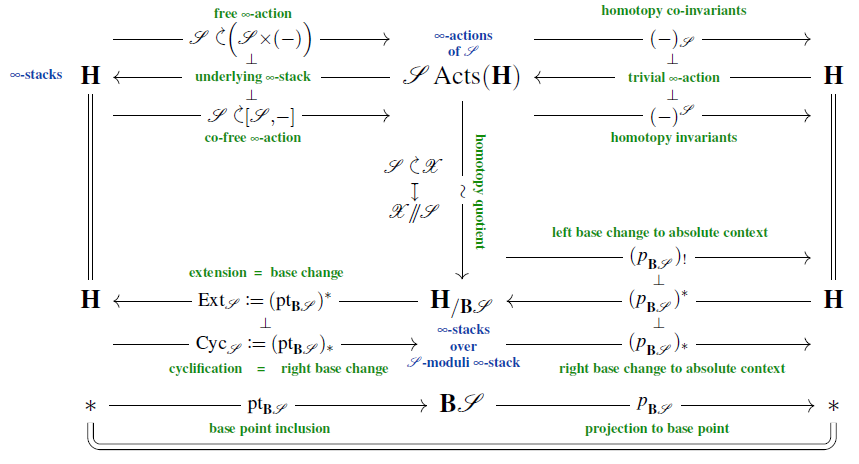
From this one may extract component models by invoking the right Quillen adjunction which encodes the derived co-free -action, discussed here.
Related concepts
References
Groupoid models that plausibly represent cyclic loop stacks are discussed (under the notation “”) in
- Zhen Huan, Def. 2.5, 2.9 in: Quasi-Elliptic Cohomology I, Advances in Mathematics, Volume 337, 15 October 2018, Pages 107-138 (arXiv:1805.06305, doi:10.1016/j.aim.2018.08.007)
following
- Nora Ganter, Section 2.1 in: Stringy power operations in Tate K-theory (arXiv:math/0701565)
Last revised on June 29, 2021 at 14:12:58. See the history of this page for a list of all contributions to it.