nLab generalized homology
Context
Cohomology
Special and general types
-
group cohomology, nonabelian group cohomology, Lie group cohomology
-
-
cohomology with constant coefficients / with a local system of coefficients
Special notions
Variants
-
differential cohomology
Extra structure
Operations
Theorems
Contents
Idea
A generalized homology theory is a certain functor from suitable topological spaces to graded abelian groups which satisfies most, but not all, of the abstract properties of ordinary homology functors (e.g. singular homology).
By the Brown representability theorem, under certain conditions every spectrum is the coefficient object of a generalized cohomology theory and S-dually of a generalized homology theory. For an Eilenberg-MacLane spectrum this reduces to ordinary homology.
See at generalized (Eilenberg-Steenrod) cohomology for more.
Definition
Reduced homology
Throughout, write Top for the category of topological spaces homeomorphic to CW-complexes. Write for the corresponding category of pointed topological spaces.
Recall that colimits in are computed as colimits in after adjoining the base point and its inclusion maps to the given diagram
Example
The coproduct in pointed topological spaces is the wedge sum, denoted .
Write
for the reduced suspension functor.
Write for the category of integer-graded abelian groups.
Definition
A reduced homology theory is a functor
from the category of pointed topological spaces (CW-complexes) to -graded abelian groups (“homology groups”), in components
and equipped with a natural isomorphism of degree +1, to be called the suspension isomorphism, of the form
such that:
-
(homotopy invariance) If are two morphisms of pointed topological spaces such that there is a (base point preserving) homotopy between them, then the induced homomorphisms of abelian groups are equal
-
(exactness) For an inclusion of pointed topological spaces, with the induced mapping cone, then this gives an exact sequence of graded abelian groups
We say is additive if in addition
-
(wedge axiom) For any set of pointed CW-complexes, then the canonical morphism
from the direct sum of the value on the summands to the value on the wedge sum, example , is an isomorphism.
We say is ordinary if its value on the 0-sphere is concentrated in degree 0:
- (Dimension) .
A homomorphism of reduced cohomology theories
is a natural transformation between the underlying functors which is compatible with the suspension isomorphisms in that all the following squares commute
Unreduced homology
In the following a pair refers to a subspace inclusion of topological spaces (CW-complexes) . Whenever only one space is mentioned, the subspace is assumed to be the empty set . Write for the category of such pairs (the full subcategory of the arrow category of on the inclusions). We identify by .
Definition
A homology theory (unreduced, relative) is a functor
to the category of -graded abelian groups, as well as a natural transformation of degree +1, to be called the connecting homomorphism, of the form
such that:
-
(homotopy invariance) For a homotopy equivalence of pairs, then
is an isomorphism;
-
(exactness) For the induced sequence
is a long exact sequence of abelian groups.
-
(excision) For such that , then the natural inclusion of the pair induces an isomorphism
We say is additive if it takes coproducts to direct sums:
-
(additivity) If is a coproduct, then the canonical comparison morphism
is an isomorphismfrom the direct sum of the value on the summands, to the value on the total pair.
We say is ordinary if its value on the point is concentrated in degree 0
- (Dimension): .
A homomorphism of unreduced homology theories
is a natural transformation of the underlying functors that is compatible with the connecting homomorphisms, hence such that all these squares commute:
Lemma
The excision axiom in def. is equivalent to the following statement:
For all with , then the inclusion
induces an isomorphism,
(e.g Switzer 75, 7.2, 7.5)
Proof
First consider the statement under the condition that .
In one direction, suppose that satisfies the original excision axiom. Given with , set and observe that
and that
Hence the excision axiom implies .
Conversely, suppose satisfies the alternative condition. Given with , observe that we have a cover
and that
Hence
This shows the statement for the special case that . The general statement reduces to this by finding a suitable homotopy equivalence to a slightly larger covering pair (e.g Switzer 75, 7.5).
Proposition
(exact sequence of a triple)
For an unreduced generalized cohomology theory, def. , then every inclusion of two consecutive subspaces
induces a long exact sequence of homology groups of the form
where
Proof
Apply the braid lemma to the interlocking long exact sequences of the three pairs , , :
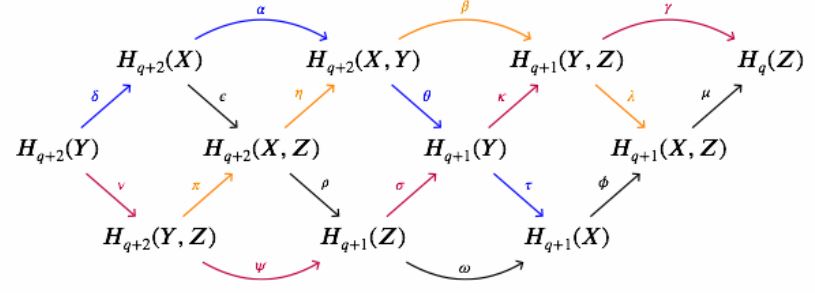
(graphics from this Maths.SE comment)
See here for details.
Properties
Expression by ordinary homology via Atiyah-Hirzebruch spectral sequence
The Atiyah-Hirzebruch spectral sequence serves to express generalized homology in terms of ordinary homology with coefficients in .
Whitehead theorem
Proposition
Let be a morphism of reduced generalized (co-)homology functors, def. (a natural transformation) such that its component
on the 0-sphere is an isomorphism. Then is an isomorphism for any CW-complex with a finite number of cells. If both and satisfy the wedge axiom, then is an isomorphism for any CW-complex, not necessarily finite.
For and ordinary cohomology/ordinary homology functors a proof of this is in (Eilenberg-Steenrod 52, section III.10). From this the general statement follows (e.g. Kochman 96, theorem 3.4.3, corollary 4.2.8) via the naturality of the Atiyah-Hirzebruch spectral sequence (the classical result gives that induces an isomorphism between the second pages of the AHSSs for and ). A complete proof of the general result is also given as (Switzer 75, theorem 7.55, theorem 7.67)
Examples
-
stable homotopy homology theory is the homology theory represented by the sphere spectrum
-
ordinary homology is the homology theory represented by an Eilenberg-MacLane spectrum
-
bordism homology theory is the homology theory represented by a Thom spectrum;
Related concepts
References
(For more see the references at generalized (Eilenberg-Steenrod) cohomology.)
Original articles include
- George Whitehead, Generalized homology theories (1961) (pdf)
Textbook accounts include
-
Stanley Kochmann, section 3.4 of Bordism, Stable Homotopy and Adams Spectral Sequences, AMS 1996
-
Robert Switzer, chapter 7 (and 8-12) of Algebraic Topology - Homotopy and Homology, Die Grundlehren der Mathematischen Wissenschaften in Einzeldarstellungen, Vol. 212, Springer-Verlag, New York, N. Y., 1975.
-
Stefan Schwede, chapter II, section 6 of Symmetric spectra, 2012 (pdf)
See also
-
Friedrich Bauer, Classifying spectra for generalized homology theories Annali di Maternatica pura ed applicata
(IV), Vol. CLXIV (1993), pp. 365-399
-
Friedrich Bauer, Remarks on universal coefficient theorems for generalized homology theories Quaestiones Mathematicae
Volume 9, Issue 1 & 4, 1986, Pages 29 - 54
A general construction of homologies by “geometric cycles” similar to the Baum-Douglas geometric cycles for K-homology is discussed in
- S. Buoncristiano, C. P. Rourke and B. J. Sanderson, A geometric approach to homology theory, Cambridge Univ. Press, Cambridge, Mass. (1976)
Further generalization of this to bivariant cohomology theories is in
- Martin Jakob, Bivariant theories for smooth manifolds, Applied Categorical Structures 10 no. 3 (2002)
Last revised on August 5, 2025 at 01:05:42. See the history of this page for a list of all contributions to it.