nLab homotopy equivalence
Context
Homotopy theory
homotopy theory, (∞,1)-category theory, homotopy type theory
flavors: stable, equivariant, rational, p-adic, proper, geometric, cohesive, directed…
models: topological, simplicial, localic, …
see also algebraic topology
Introductions
Definitions
Paths and cylinders
Homotopy groups
Basic facts
Theorems
Equality and Equivalence
-
equality (definitional, propositional, computational, judgemental, extensional, intensional, decidable)
-
identity type, equivalence of types, definitional isomorphism
-
isomorphism, weak equivalence, homotopy equivalence, weak homotopy equivalence, equivalence in an (∞,1)-category
-
Examples.
Contents
Definition
A homotopy equivalence between topological spaces (or other objects in a category equipped with a notion of homotopy) and is a morphism which has a homotopy inverse, hence such that there exists a morphism and homotopies and .
(Note the similarity with the strict notion of equivalence of categories.)
If there exists a homotopy equivalence between and we say that and are homotopy equivalent or that they have the same homotopy type. Being homotopy equivalent is evidently an equivalence relation.
For many purposes, one wants instead weak homotopy equivalences. Often when speaking of a homotopy equivalence or a homotopy type, one actually means the weak version. (This is especially likely on this wiki, due to the relationship to -infinity-groupoids suggested by the homotopy hypothesis.)
The homotopy category of Top with respect to homotopy equivalences is Ho(Top).
Examples
Example
The following three graphs

(i.e. the evident topological subspaces of the plane that these pictures indicate) are not homeomorphic. But they are homotopy equivalent, in fact they are each homotopy equivalent to the disk with two points removed, by the homotopies indicated by the following pictures:
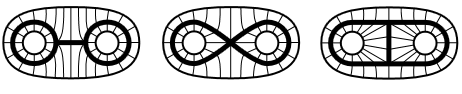
graphics grabbed from Hatcher
More generally, in any (∞,1)-category other than Top, a homotopy equivalence in is just an equivalence in .
Properties
Any homotopy equivalence is also a weak homotopy equivalence. Conversely, in the context of topological spaces, any weak homotopy equivalence between m-cofibrant spaces (spaces that are homotopy equivalent to CW complexes) is a homotopy equivalence. This is the Whitehead theorem.
The homotopy equivalences are the weak equivalences in the Strøm model structure on topological spaces. The homotopy category resulting from inverting all homotopy equivalences in Top is the same as that resulting from identifying homotopic maps.
Strong homotopy equivalences
Sometimes an apparently stronger form of homotopy equivalence is needed. These seem to have been first noticed by Richard Lashof in 1970 in work on triangulation and smoothing. The point is one of the interaction between the two homotopies, which are not made explicit in the definition above. Let us set this up slightly differently:
In a homotopy equivalence there are the two maps and , then two homotopies
and
The whiskering actions of maps on homotopies (and more generally in any (∞,1)-category or category with a cylinder functor) gives two homotopies , namely and . Similarly, of course, there are two homotopies , namely and . In the usual definition of homotopy equivalence, there is no coherence required between these. That is handled precisely by the notion of strong homotopy equivalence. More precisely Lashof defined
Definition
A strong homotopy equivalence between spaces and is a quadruple , as above, such that and .
Thus this imposes a minimal coherence condition on the data making up the homotopy equivalence. The definition clearly can be generalised to any reasonable setting with a notion of homotopy.
For example, in a 2-category where a homotopy is a natural isomorphism, and a homotopy between homotopies is just an equality, a homotopy equivalence is simply an equivalence, while a strong homotopy equivalence is the same as an adjoint equivalence.
The question naturally arises as to whether all homotopy equivalences are strong. Rainer Vogt(1972) proved
Vogt’s Lemma
If be a morphism that is a homotopy equivalence in , let be a homotopy inverse and a homotopy. Then there is a homotopy such that is a strong homotopy equivalence.
Various versions of this are known in other settings, e.g. -enriched categories. In a 2-category the corresponding fact is that any equivalence can be improved to an adjoint equivalence, by changing at most one of the 2-cell isomorphisms involved.
Note, though, that the coherence supplied by Vogt’s lemma is not required to continue to higher levels. There is no condition of compatibilty between the two ‘homotopies between the homotopies’. In some situations, at least, some higher compatibility is known to be derivable; for instance, any biequivalence in a 3-category can be improved to an adjoint biequivalence.
Vogt’s Lemma plays a key role in the proof of Vogt’s theorem (cf. homotopy coherent diagrams).
Related concepts
-
homotopy equivalence, weak homotopy equivalence
References
Textbook accounts:
-
Allen Hatcher, Algebraic Topology, Cambridge University Press (2002) [ISBN:9780521795401, webpage]
-
Anatoly Fomenko, Dmitry Fuchs, §3.3 in: Homotopical Topology, Graduate Texts in Mathematics 273, Springer (2016) [doi:10.1007/978-3-319-23488-5, pdf]
Last revised on November 21, 2024 at 14:29:05. See the history of this page for a list of all contributions to it.