nLab braid lemma

Statement

Proposition

(braid lemma)

Given a commuting diagram of abelian groups of the following form

$$\array{ && A && \longrightarrow && B && \longrightarrow && C && \longrightarrow && D \\ & \nearrow && \searrow && \nearrow && \searrow && \nearrow && \searrow && \nearrow \\ E && && F && && G && && H \\ & \searrow && \nearrow && \searrow && \nearrow && \searrow && \nearrow \\ && I && \longrightarrow && J && \longrightarrow && K } \,.$$

Consider the following four sequences inside the diagram

1. $E\to A \to B \to G \to K$;

2. $E \to I \to J \to G \to C \to D$;

3. $A \to F \to J \to K \to H \to D$;

4. $I \to F \to B \to C \to H$.

Then: if the first three of these are long exact sequences and the fourth is a chain complex, then the fourth is also long exact.

(Munkres, §26, Exc.)

Applications

Long exact sequence of a triple in homology

Given a generalized homology theory $H_\bullet$, then by definition for every inclusion $A \hookrightarrow X$ of topological spaces, there is an long exact sequence

$$\cdots \to H_{n+1}(X,A) \overset{\delta}{\longrightarrow} H_n(A) \longrightarrow H_n(X)\longrightarrow H_n(X,A) \to \cdots \,.$$

Proposition

For $H_\bullet$ an unreduced generalized homology theory and for two consecutive inclusions $Z \hookrightarrow Y \hookrightarrow X$ (a “triple” $(X, Y, Z)$) there is a long exact sequence of the form

$$\cdots H_{n+1}(X,Y) \to H_{n}(Y,Z) \to H_n(X,Z) \to H_n(X,Y) \to \cdots \,.$$

Dually for generalized (Eilenberg-Steenrod) cohomology.

Proof

Consider the following braid diagram

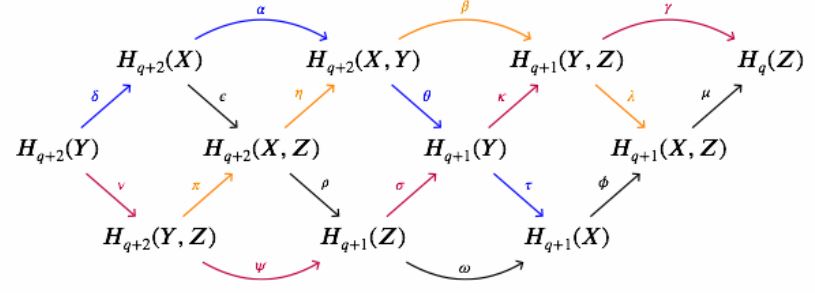
(graphics from this Maths.SE comment)

The blue, purple and the black sequence are the exact sequences of the pairs $(X,Y)$, $(Z,Y)$ and $(Z,X)$, respectively. The orange sequence is a chain complex by these exact sequences and using the commutativity of the diagram, and because the diagonals $H_\bullet(Y,Z) \to H_\bullet(X,Z) \to H_\bullet(X,Y)$ factor through $H_\bullet(Y,Y) = 0$. Hence the braid lemma, prop. , implies the claim.

References

• Munkres, p. 148 of Elements of algebraic topology